求解受力平衡问题的多种方法赏析
■山东省菏泽市第三中学 闫雨华
方法一:合成与分解法
利用力的合成与分解能够解决三力平衡问题,求解时有两种思路:一是将其中一个力沿另两个力的反方向进行分解,将三力转化为四力,构成两对平衡力,根据平衡条件列式求解;二是将其中两个力进行合成,将三力转化为二力,构成一对平衡力,根据平衡条件列式求解。
例1(1)如图1甲所示,质量为m的物块静置在粗糙斜面上,斜面倾角θ=30°,求斜面受到的压力和摩擦力。

图1
(2)如图1乙所示,轻绳一端固定在天花板上的O点,另一端系住一个质量为m的物块,物块静置在光滑斜面上,斜面倾角θ=30°,轻绳与竖直方向之间的夹角也为θ=30°,求轻绳受到的拉力及斜面受到的压力。
解析:(1)对物块进行受力分析,如图2甲所示,物块在重力mg、斜面对它的支持力N、摩擦力f的作用下处于平衡状态,根据平衡条件可得,将重力mg沿平行于斜面方向和垂直于斜面方向分解,则重力mg沿平行于斜面方向的分力与摩擦力f,重力mg沿垂直于斜面方向的分力与支持力N,构成两对平衡力,根据几何关系得N=mgcosθ=。根据牛顿第三定律可知,斜面受到的压力,方向垂直于斜面向下;斜面受到的摩擦力f'=,方向沿斜面向下。
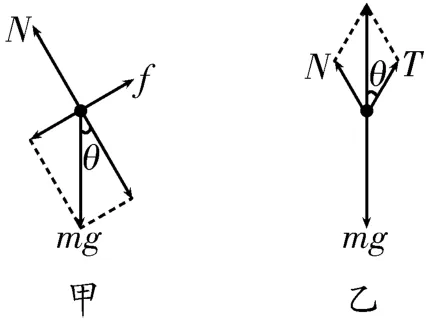
图2
(2)对物块进行受力分析,如图2 乙所示,物块在斜面对它的支持力N、轻绳的拉力T、重力mg的作用下处于平衡状态,根据平衡条件可得,支持力N与拉力T的合力与重力mg构成一对平衡力,根据几何关系得。根据牛顿第三定律可知,物块对斜面的压力,方向垂直于斜面向下;轻绳受到的拉力T'=,方向沿轻绳斜向下。
方法二:正交分解法
正交分解法是指将物体受到的各力分解到相互垂直的x轴和y轴上,运用物体在两坐标轴上受到的合外力等于零列式求解,这种方法多用于求解物体在三个以上共点力作用下的平衡问题。x轴、y轴方向选择的原则:(1)在平衡状态下,少分解力或将容易分解的力进行分解;(2)在非平衡状态下,通常沿加速度方向和垂直于加速度方向进行分解;(3)尽量不要分解未知力。
例2如图3所示,斜劈A静置在水平地面上,质量为m的物体B在外力F1和F2的共同作用下沿斜面向下运动。当外力F1的方向水平向右,外力F2的方向沿斜面向下时,斜劈A受到地面的摩擦力方向向左,则下列说法中正确的是( )。
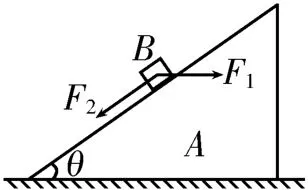
图3
A.若同时撤去外力F1和F2,则物体B的加速度方向一定沿斜面向下
B.若只撤去外力F1,则在物体B仍向下运动的过程中,斜劈A所受地面摩擦力的方向可能向右
C.若只撤去外力F2,则在物体B仍向下运动的过程中,斜劈A所受地面摩擦力的方向可能向右
D.若只撤去外力F2,则在物体B仍向下运动的过程中,斜劈A所受地面摩擦力的方向不变
解析:对物体B和斜劈A分别进行受力分析,如图4所示。斜劈A在水平方向上受力平衡,且斜劈A受到地面的摩擦力方向向左,对斜劈A有NB'sinθ>fB'cosθ,fB'=fB=μNB,NB'=NB,即μ<tanθ。当同时撤去外力F1、F2时,对物体B有mgsinθ>μmgcosθ,即物体B的加速度方向一定沿斜面向下,选项A 正确。若只撤去外力F1,则在物体B仍向下运动的过程中,对物体B有NB=mgcosθ,fB=μmgcosθ<mgsinθ,对斜劈A有NB'sinθ>fB'cosθ,即斜劈A所受地面摩擦力的方向仍向左,选项B 错误。若只撤去外力F2,则在物体B仍向下运动的过程中,斜劈A所受地面摩擦力的方向仍向左,选项C错误,D 正确。

图4
答案:AD
方法三:整体法和隔离法
选择研究对象是解决物理问题的首要环节。若一个平衡问题中涉及两个或两个以上物体,则在选取研究对象时,要灵活运用整体法和隔离法。如果不需要求物体间的相互作用力,那么优先采用整体法,这样涉及的研究对象少,未知量少,方程少,求解简便;多数情况下,往往需要采用整体法和隔离法相结合的方法分析与求解。
例3如图5所示,顶端装有定滑轮的斜面体放置在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态(不计细绳的质量、细绳与滑轮间的摩擦)。现用水平向右的力F作用在物体B上,将物体B缓慢拉高一定的距离,在此过程中斜面体与物体A仍然保持静止状态。下列说法中正确的是( )。
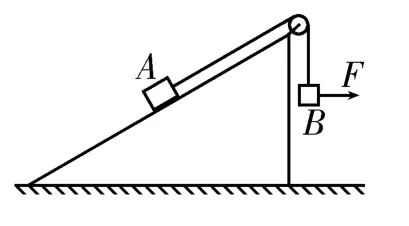
图5
A.力F一定逐渐变小
B.斜面体所受地面的支持力一定变大
C.物体A所受斜面体的摩擦力一定变大
D.地面对斜面体的摩擦力一定变大
解析:选物体B为研究对象进行受力分析,如图6所示,则。在物体B被缓慢拉高的过程中,θ增大,则水平力F随之变大,选项A 错误。对由A、B两物体和斜面体组成的整体而言,斜面体与物体A仍然保持静止状态,在水平方向上受到力F和地面对它的摩擦力的作用,随着力F的增大,地面对斜面体的摩擦力一定变大,在竖直方向上受到的重力和支持力保持不变,则斜面体所受地面的支持力不变,选项B错误,D 正确。在物体B被缓慢拉高的过程中,尽管细绳的张力变大,但是因为不知道初始状态下物体A所受斜面体的摩擦力的方向,所以无法确定物体A所受斜面体的摩擦力的变化情况,选项C错误。

图6
答案:D
方法四:图解法
图解法适用于一个物体受到三个力(或可等效为三个力)作用而处于平衡状态的问题,特别是物体的动态平衡问题或物体受力平衡中的临界和极值问题。
例4如图7所示,光滑的小球静止在斜面和竖直放置的木板之间,已知小球的重力为G,斜面的倾角为θ,现使木板沿逆时针方向绕O点缓慢移动,小球对斜面和挡板的压力怎样变化?

图7
解析:选小球为研究对象,进行受力分析,如图8所示,小球受重力G、斜面的支持力N1和木板的支持力N2三个力作用,处于平衡状态,这三个力构成力的矢量三角形。木板绕O点缓慢移动,小球处于动态平衡状态。木板对小球的支持力N2的方向与竖直方向之间的夹角由90°缓慢减小,重力G的大小和方向都不变,斜面对小球的支持力N1的方向也不变,由矢量三角形可知,N1将逐渐变小,N2将先变小后变大。

图8
方法五:相似三角形法
“相似三角形”的主要性质是对应边成比例,对应角相等。当涉及矢量运算,又构建了矢量三角形时,若矢量三角形与图中的某个几何三角形为相似三角形,则可利用相似三角形法解题。
例5如图9所示,A、B两球通过劲度系数为k1的轻弹簧相连,小球B用长为L的细绳悬于O点,小球A固定在O点正下方的支架上,且小球A到O点的距离恰为L,系统平衡时细绳所受的拉力为F1。现把A、B两球间的弹簧换成劲度系数为k2的轻弹簧,仍使系统处于平衡状态,此时细绳所受的拉力为F2,则F1与F2的大小关系为( )。

图9
A.F1>F2B.F1=F2
C.F1<F2D.无法确定
解析:选小球B为研究对象,进行受力分析,如图10所示,小球B受到重力G、弹簧的弹力F和细绳的拉力T三个力作用,根据数学知识可知,图中△OAB(几何三角形)与△BGT'(矢量三角形)相似,因为OA=OB,所以细绳的拉力T'等于小球B的重力G,即F1=F2=G。

图10
答案:B
方法六:正弦定理法
物体受到三个力作用处于平衡状态时,三个力的合力为0,三个力可构成一个封闭的矢量三角形,若由题设条件可以寻找到角度关系,则可利用正弦定理列式求解。
例6一盏电灯的重力为G,悬于天花板上的A点,在电线上的O处系一细线OB,使电线OA与竖直方向之间的夹角β=30°,如图11所示。现保持β角不变,缓慢调整细线OB的方向至细线OB的张力最小,此时细线OB与水平方向之间的夹角α等于多少? 细线OB的最小张力是多少?

图11
解析:选O点为研究对象,进行受力分析,如图12所示,根据三力平衡特点可知,电线OA、细线OB对O点的作用力TA、TB的合力T与电灯的重力G等大反向,即T=G。在△OTBT中,∠TOTB=90°-α,又有∠OTTB=∠TOA=β,故∠OTBT=180°-(90°-α)-β=90°+α-β,根据正弦定理得解 得TB=因为β角不变,所以当α=β=30°时,TB最小,且。

图12

