高考物理模拟试题(一)参考答案与提示

1.C 提示:目前世界上的核动力航母利用的是重核的裂变,选项A 错误。提高温度不可以改变放射性元素的半衰期,选项B 错误。卢瑟福发现质子的核反应方程是,选项C 正确。发生核反应时满足质量数守恒和电荷数守恒,质量会有亏损,选项D 错误。

2.B 提示:小球被抛出后做平抛运动,根据平抛运动规律得,解得,选项A 错误。火星的第一宇宙速度即近火卫星的运行速度,则,选项B 正确。以位于火星表面的物体为研究对象,则mg,解得火星的质量,选项C错误。火星的平均密度,选项D 错误。

3.C 提示:选O点为研究对象,进行受力分析,如图1所示,根据平衡条件得Tacosθ1+Tbcosθ2=Tc,Tasinθ1=Tbsinθ2,又有Ta=mag,Tb=mbg,Tc=mg,ma=300g,mb=500g,根据数学知识得θ1＞θ2,m＞400g。

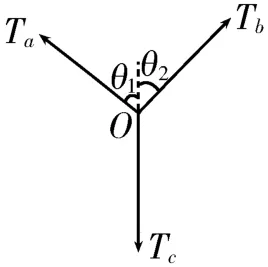
图1

4.A 提示:子弹射入木块的时间极短,瞬间动量守恒,根据动量守恒定律得mv0=(M+m)v,解得。木块自被子弹击中前到第一次回到原来位置的过程中,根据动量定理得木块受到的合外力的冲量大小。

5.C 提示:若粒子从ab边中点处垂直于ab边射出,则其运动轨迹的圆心一定在ab边上,设圆心与ab边的交点为g,则圆心在Og连线的中垂线上,而该中垂线与ab边平行,不可能相交,选项A 错误。粒子从a点垂直于af边射出,f点为其运动轨迹的圆心,对应的圆心角为60°,因此粒子在磁场中的运动时间,又有,解得,选项B 错误。垂直于cf连线向上发射的粒子刚好能离开磁场时,其运动轨迹与af边相切,根据几何关系得,根据qvB得,解得,选项C 正确。因为O点距磁场正六边形边界的最近距离,即d对应粒子刚好离开磁场的运动轨迹的最小直径,所以粒子运动轨迹的最小半径,又有,解得,选项D 错误。

6.BD 提示:小球沿直线AB运动,受到的合外力沿AB方向,小球的受力情况如图2所示,则qEtan 45°=mg,解得,选项A错误。小球所受合外力,根据匀变速直线运动规律得小球到达B点时的速度v=,根据牛顿第二定律得加速度。设A、B两点间的距离为L,根据动能定理得,解得静电力做功。根据W=qUAB,解得。根据UAB=φA-φB,且A点的电势为零,解得φB=,则B点的电势能EB=qφB=,选项B 正确,C 错误。小球机械能的变化量等于静电力做的功,则ΔE=W=,选项D 正确。

图2

7.CD 提示:根据u-t图像得输入电压的周期T=0.02 s,则,输入电压的最大值Umax=20 2 V,因此输入电压的瞬时值表达式为u=20 2sin(100πt) V,选项A 错误。只断开开关S2后,负载电阻增大为原来的2倍,副线圈电压不变,则副线圈中的电流减小为原来的一半,灯泡L1、L2的功率均变为额定功率的四分之一,即灯泡L1、L2均不能正常发光,选项B 错误。只断开开关S2后,负载电阻变大,副线圈中的电流变小,输出功率变小,则原线圈的输入功率减小,选项C正确。将开关S1换接到2后,电阻R两端电压的有效值为4 V,则电阻R消耗的电功率,选项D正确。

8.AD 提示:细杆由静止运动至细杆前端到达C点的过程中,根据动能定理得,解得,选项A 正确。细杆前端过C点后,在C点右侧的部分受到摩擦力作用,设杆长为l,C点右侧部分的长度为x,则,解得。又有细杆受到的摩擦力f=μN=μm'g=,根据牛顿第二定律得a=。当细杆后端过C点后,细杆受到的摩擦力f=μmg,解得a=μg,保持不变。因此细杆受到的摩擦力f随x变化的图像如图3所示,即细杆先做加速度变大的减速运动,后做匀减速运动,选项B错误。取细杆左侧长为x0的一段为研究对象,当细杆全部进入C点右侧时,有,对整体有μmg=ma,则μm1g-F=m1a,解得F=0,即细杆前后两段间无弹力。当细杆左侧长为x0这段还没全部进入C点右侧时,有,解得。对细杆左侧长为x0这段有F=m1a≠0,可见细杆前一段对后一段的作用力大小不等,选项C错误。细杆从其前端过C点到全部进入C点右侧的过程中,有,细杆从全部进入C点右侧到停止运动的过程中,有。根据动能定理得,解得,选项D正确。

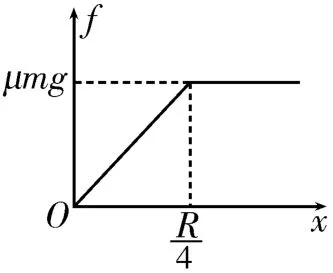
图3

9.(1)×1 k (2)+插孔 -接线柱(3)1 900 1.7 (4)如图4所示 (5)4.7 kΩ 0.59 mA

图4

10.(1)将钢球置于轨道平直段各处,都能保持静止,说明斜槽末端水平 (2)球心(3

11.(1)设物块2 到达传送带A端时的速度为vA,根据动能定理得m(gsinθ-,解得vA=。设两物块碰后黏合体的速度为,根据动量守恒定律得mvA=2mvA',解得。(2)设黏合体沿光滑半圆形轨道CDE上升的最大高度为h,根据动能定理得2mvA'2,解得h=0.5 m,即黏合体从C点沿光滑半圆形轨道CDE运动到与圆心等高的D点速度减小为0,再从D点返回至停止运动。根据动能定理得2mgh-2μmgs路=0,解得s路=1 m,即黏合体最后停在传送带B端。(3)设黏合体到达E点时的速度为vE,根据平抛运动规律得,解得。黏合体从B点运动到E点,根据动能定理得-2μmg·2d-2mg·2R=,解得。因为vB＜vA',所以黏合体在传送带上做减速运动。若黏合体从A点一直做减速运动到B点,根据动能定理得,解得。因为vB＞v,所以黏合体在传送带上先做减速运动后做匀速运动,传送带的转动速度v传=。

12.(1)设导体棒1刚进入磁场区域时的速度为v,根据动能定理得,解得。此时回路中的感应电动势最大,且E=BLv,回路中的感应电流I=,导体棒2 受到的安培力F=BI·2L,导体棒2的最大加速度满足F=2ma,解得。(2)导体棒1 进入磁场后做减速运动,导体棒2做加速运动,当v1=2v2时,回路中的感应电动势为0,感应电流为0,两导体棒分别达到稳定的匀速运动状态,导体棒1 在水平轨道上运动的过程中有,导体棒2 在水平轨道上运动的过程中有,解得。(3)两导体棒刚好达到稳定状态时,整个回路中产生的热量,导体棒1中产生的热量,解得。

13.(1)ADE (2)(ⅰ)设玻璃管的横截面积为S,则右侧管内封闭空气柱的初状态体积V右1=5S,环境温度升高的过程中右侧管内封闭空气柱的压强不变,根据盖-吕萨克定律得,解得右侧管内封闭空气柱的长度L=5.83 cm。(ⅱ)大气压强p0=75 cmHg,右侧管内封闭空气柱的初状态压强,左侧管内封闭空气柱的初状态压强90 cmHg,左侧管内封闭空气柱的初状态体积V左1=32S。环境温度升高后,设左侧管内水银面下降的高度为h,左侧管内封闭空气柱的末状态压强,左侧管内封闭空气柱的末状态体积V左2=(32+h)S。对左侧管内封闭空气柱应用理想气体状态方程得,解得h=3 cm。

14.(1)ACE (2)(ⅰ)光束a经折射后恰好射到AD边的中点,如图5所示,根据几何关系得,根据折射率公式得n=,解得。(ⅱ)设光束a在AD边上刚好发生全反射,则光束a在P点的折射角β满足解得。根据数学知识得,根据折射率公式得,解得。当光束a经折射后刚好射到D点时,有sinβ,根据,解得。因此光束a在AD边上发生全反射,sinθ的取值范围为。

图5