多波束测深Ping 周期内姿态变化对水深的影响分析

吴冬强，王晓明，卜宪海，于宗泽

（1.自然资源部海底矿产资源重点实验室 中国地质调查局广州海洋地质调查局，广东 广州 511458；2.中交星宇科技有限公司，北京 101399；3.山东科技大学测绘与空间信息学院，山东 青岛 266590）

多波束测深波束归位[1]计算过程涉及参数较多，同时受海洋复杂环境的影响，Ping 周期换能器姿态存在动态变化，进一步加剧了波束归位计算的复杂性，而姿态改正作为波束归位中的重要环节之一，其产生的影响对于后续多波束精细化处理至关重要。

对于多波束瞬时姿态影响，国内外学者进行了大量的研究。2001年，赵建虎等[2]分析了测船瞬时姿态各参数的受动因素，并给出各角度所带来误差的计算公式；2009年，阳凡林等[3]考虑到水下声线弯曲对波束归位的影响，提出瞬时波束向量是安装偏差和姿态影响的综合产物，并据此推导了顾及安装偏差角和姿态角影响的瞬时波束向量计算的数学模型；2015年，于家成等[4]基于载体姿态效应分别对位于水平海底和倾斜海底的波束脚印进行改正，最终得到精度更高的水深图；2019年，金绍华等[5]考虑姿态和声线弯曲对测量影响的耦合效应，推导了海底测深点位置和水深归算模型；陈若婷等[6]、肖元弼等[7]针对横摇变化导致测深数据误差问题，分别于2013年和2021年提出了基于横摇稳定和利用回波时间反演横摇角的方法，提高了波束脚印位置的计算精度；HARE R 等剖析了多波束测深过程中的各项误差源，推导了测深点水深及平面位置的误差估计模型，并提出了用于多波束测深不确定度计算的HGM（Hare-Godin-Mayer）模型[8-9]。然而，上述研究成果均将多波束发射和接收换能器近似看作一体（本文称之为收发同体模型），仅利用波束发射或接收时刻的单一姿态进行波束归位，未顾及Ping周期内的换能器姿态变化，此外，为保障海底全覆盖，纵摇和艏摇实时补偿技术也应用于多扇区多波束[10-11]系统，使得发射导向角成为波束入射向量的组成部分，在此影响下，收发换能器Ping 周期内姿态变化的影响进一步加剧。2004年，加拿大新布伦瑞克大学教授HUGHES CLARKE J E[12]利用波束传播过程中涉及的所有参数提出一种波束归位方法——虚拟同心（Virtual Concentric Array，VCCA）模型，模型将多波束收发换能器分开考虑，可更为精确地计算水深结果。

综合现有研究，正确分析Ping 周期内换能器姿态所产生的影响可为多波束数据精细化处理提供一定的参考，因此，本文依据多波束测深原理，并基于VCCA 模型，利用模拟数据和实测数据分析波束收发过程内姿态变化，以及在发射导向角共同作用下对波束点水深的影响。

1 瞬时姿态影响分析

波束发射时刻的姿态主要影响发射波束能量与海底平面的相交过程，导致其偏离理想的位置；波束接收时刻的姿态主要影响接收换能器对波束脚印回波信息的接收，导致信号接收时换能器理想状态被打破，进而使得测得的波束入射角存在误差。

对比收发同体模型和VCCA 模型可知，前者在计算波束入射向量时利用了收发换能器整体的安装偏差、波束入射角，以及接收时刻横摇和发射时刻纵摇、航向，而后者使用了收发换能器各自安装偏差角、收发时刻两换能器瞬时姿态及波束发射与波束入射角等参数。结合波束形成和波束导向原理[12]可知，发射时刻横摇和接收时刻纵摇对波束能量在海底投影影响微小，因此本节对发射时刻纵摇、航向和接收时刻横摇、航向，以及在发射导向角共同作用下其对波束入射向量计算产生的影响进行分析。

1.1 接收时刻横摇

若将发射和接收换能器看作整体，其换能器声学中心可假定位于发射换能器与接收换能器米尔斯交叉点附近[13-14]。如图1 所示，波束接收（Beam Receive，BR）时刻横摇会对接收波束能量产生明显偏转，当波束入射角增大时，波束在海底投影形成的曲线曲率增加，开口变窄[15]，在无其他角度影响时，其角度偏差大小为横摇值，波束脚印实际位置由a点变化为b 点；在发射导向角的共同影响下，波束脚印实际位置变化为c 点，且该误差随发射导向角和波束入射角的增大而逐渐扩大。

图1 接收时刻横摇影响示意图

结合两模型，此时，在横摇和发射导向角的共同作用下，单位波束入射向量计算偏差值[12，16]如下。

式中，r 为接收时刻横摇角；Tsteer为发射导向角；Rsteer为波束入射角。

1.2 发射时刻纵摇

波束发射（Beam Transmit，BT）时刻纵摇使得发射换能器绕换能器坐标系[16]Y 轴在XOZ 面内发生旋转，造成发射波束能量沿航迹线方向发生前后位移，进而产生大小为纵摇值的角度偏移。如图2 所示，受波束发射时刻纵摇影响，波束脚印实际位置由a 点变化至b 点，在发射导向角的共同作用下变化为c 点。

图2 发射时刻纵摇影响示意图

结合两模型，此时在纵摇和发射导向角的共同作用下，单位波束入射向量计算偏差值[12，16]如下。

式中，p 为接收时刻纵摇角。

1.3 发射时刻航向、接收时刻航向

受测量环境复杂因素影响，测船实际航向方向并不会与测线方向一致，且在Ping 周期内波束发射与接收存在一定差别，进而使得波束扇面绕换能器坐标系Z 轴在水平面上产生扭动[17]。如图3 所示，受波束发射时刻航向影响，发射波束能量产生大小约为航向值的角度偏转，波束脚印实际位置由a 点变化为b 点；受接收时刻航向影响，波束脚印位置由a 点变化为c 点；若同时顾及发射与接收时刻航向影响，波束脚印实际位置由a 点变化为d 点。同时可知，当存在发射导向角的共同作用时，上述两时刻航向产生的误差会随发射导向角增大而逐渐扩大。

图3 发射与接收时刻航向影响示意图

结合两模型，在收发时刻航向和发射导向角的共同影响下，单位波束入射向量计算偏差值[12，16]如下（为简化书写，部分表达式以A、B 代替）。

式中，h1、h2分别为发射时刻和接收时刻航向；δ 为瞬时发射向量和瞬时接收向量的夹角[12]；A、B及δ 计算公式如下。

综上，波束发射与接收时刻姿态对测深结果产生不可忽视的影响，尤其是两时刻的航向变化会对测深点X、Y、Z 坐标均产生影响，在发射导向的作用下姿态对测深结果的影响进一步扩大，随水深增加测深结果（尤其是边缘波束）极大可能会超出规范要求；同时也可知，对于收发同体模型，其与实际波束脚印位置间的计算误差来源于接收时刻航向、发射导向及各角度间可能存在的耦合误差。

2 Ping 周期内姿态变化影响分析

结合第1 节可知，波束发射与接收时刻的某一瞬时姿态会对入射向量产生影响且在存在发射导向角情况下影响进一步增大。因此，针对Ping 周期内姿态变化所产生的影响，本节使用收发同体和VCCA 两种模型，首先利用MATLAB 进行单一姿态角变化影响的模拟实验；然后选取实测数据，通过对比数据结果分析综合姿态变化，以及在发射导向作用下对水深计算结果的影响。

2.1 模拟实验分析

本节分别分析波束发射与接收过程中横摇、纵摇和航向变化，以及在发射导向角作用下对水深计算结果的影响。设置波束入射角为10°和60°分别代表中央波束与边缘波束，姿态角度在0°～3°内变化，以发射导向角0°和3°设置两组数据，同时为简化运算过程，除实验测试参数外，安装偏差角和其余姿态角均假设为0°，数据参数如表1 所示。

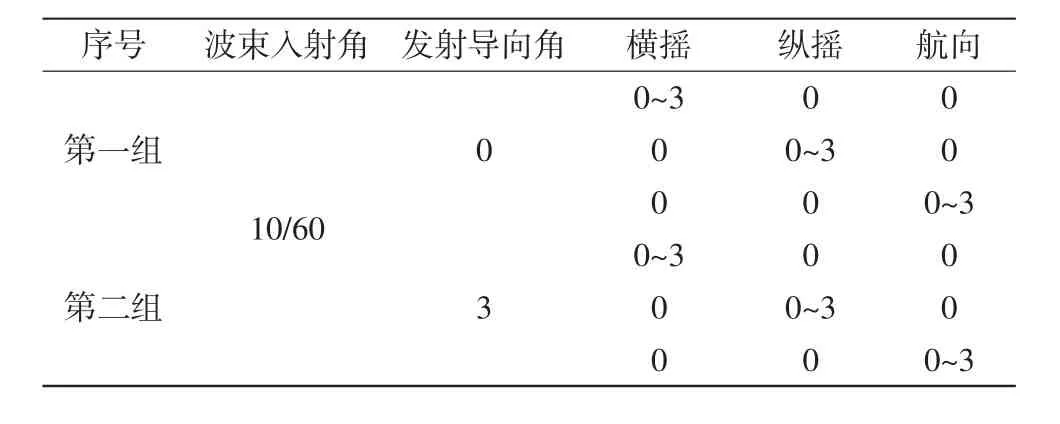
表1 模拟实验参数设置单位：（°）

利用VCCA 模型对表1 数据进行处理，计算水深相对变化，结果如图4 所示。其中，图4（a）和图4（b）分别表示发射导向角为0°和3°时各姿态角度变化所产生的水深相对变化。

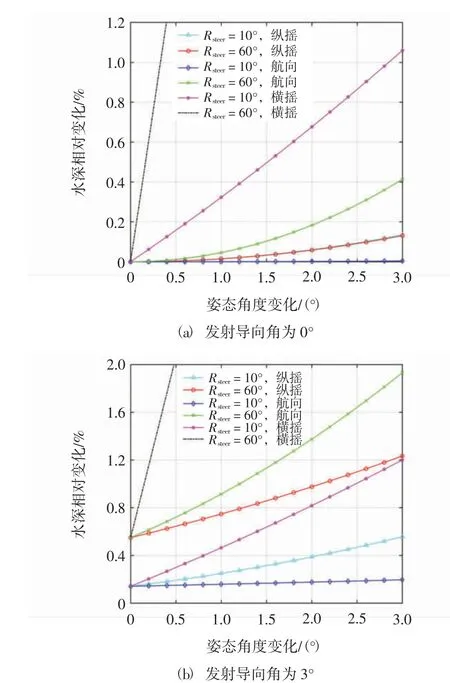
图4 姿态变化对水深的影响

从图4 可知，①相较于纵摇和航向变化，横摇变化对水深结果影响更大，且对边缘波束影响远大于中央波束，即便是微小的角度变化也会使得边缘波束易超出水深测量精度要求；②纵摇变化对中央波束和边缘波束影响近似，但随发射导向角数值而逐渐对边缘波束产生更大影响；③对于中央波束，除横摇变化外，其受纵摇变化影响较航向变化影响大，边缘波束则反之；④当存在发射导向角时，会加剧姿态变化对水深结果的影响，进一步影响测深精度；⑤由第1 节可知，收发同体模型误差来源于接收时刻航向及发射导向角，在两者共同影响下，中央波束和边缘波束的水深相对变化约为0.2%和1.9%，若同时顾及横摇影响，水深相对误差扩大为1.1%和9.2%。

2.2 实测数据分析

选取无发射导向作用的浅水数据、带发射导向作用的浅水数据和带发射导向作用的深水数据，三组数据信息如表2 所示。三组数据地形图如图5 所示。其中，图5（a）、图5（b）、图5（c）分别对应表2 中1、2、3 三组数据中用于计算结果比对的测线地形图，红框区域为用于精度评定的与检查测线重叠部分。

表2 实测数据参数

图5 选取测线数据光照地形图

利用收发同体模型和VCCA 模型对三组数据进行处理，统计两算法水深偏差，并利用Global Mapper软件提取部分中央波束与边缘波束的水深偏差，同时对交叉重叠部分数据进行精度评定，进一步说明姿态变化和发射导向角的影响。其中，对比1、2组数据可以分析在存在发射导向角的情况下姿态变化所产生的影响；对比2、3 组数据可以分析姿态变化随水深增加所产生的影响；对比1、3 组数据可以分析在发射导向角的作用下，姿态变化随水深增加而产生的影响。

2.2.1 无导向浅水数据

利用两模型对第1 组数据进行处理，计算两模型水深差值并提取部分中央波束和边缘波束结果，并对结果进行统计，如表3 和图6 所示（统计结果为差值的绝对值）。其中，图6（a）为两算法水深计算差值，图6（b）为提取的部分中央波束与边缘波束水深差值。

表3 无导向作用浅水区两种模型计算对比分析结果

图6 收发同体模型与VCCA 模型水深计算差值

结合表3 和图6 可知，对于无导向作用的浅水数据，两算法水深误差在0～0.54 m，均值约为0.01 m，约有98%误差分布在0.2 m 内；中央波束误差与边缘波束误差均值分别约为0.005 m 和0.007 m，误差相对较小。对测线重叠部分数据进行精度评定，并参照水运工程测量规范[18]中相关精度要求进行统计，结果如表4 所示，此时两模型精度结果近似，姿态变化产生的影响并不明显。

表4 无导向作用浅水区两种模型计算结果精度评定

2.2.2 带导向作用浅水数据

利用两模型对第2 组数据进行处理，计算两模型水深差值并提取部分中央波束和边缘波束结果，并对结果进行统计，如表5 和图7 所示（统计结果为差值的绝对值）。参照《水运工程测量规范》（JTS 131—2012） 中相关精度要求进行精度评定，结果如表6 所示。

表5 带导向作用浅水区两种模型计算对比分析结果

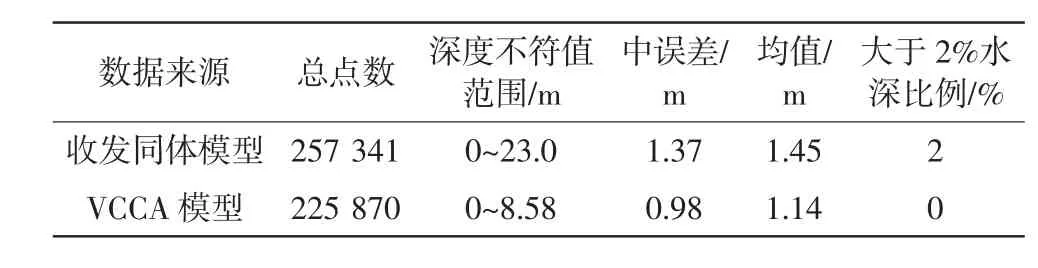
表6 有导向作用浅水区两种模型计算结果精度评定

图7 收发同体模型与VCCA 模型水深计算差值

对水深差值进行统计并结合图7 可知，对于带导向浅水数据，两算法水深误差在0～18.43 m，均值为0.47 m，约有89.3%数据误差分布在1.0 m 内，且存在部分较大误差的数据（约1.4%数据误差大于2.0 m）；选取的中央波束与边缘波束误差均值分别约为0.38 m 和0.57 m，水深误差在1.0 m 内的数据占比分别约为94.8%和83.6%。同时由表6 可知，收发同体模型深度不符值中误差及均值较VCCA 模型大，且存在部分超出2%水深精度的点。对比2.2.1 数据可知，第2 组数据姿态变化较第1 组较小，但在发射导向角的综合作用下，姿态变化所产生的影响凸显。

2.2.3 带导向作用深水数据

同样利用两模型对第3 组数据进行处理，计算两模型水深差值并提取部分中央波束和边缘波束结果，统计结果如表7 和图8 所示（统计结果为差值的绝对值）。对重叠区域进行精度评定，结果如表8所示。

表7 带导向作用深水区两种模型计算对比分析结果

表8 带导向作用深水区两种模型计算结果精度评定

图8 收发同体模型与VCCA 模型水深计算差值

对水深差值进行统计并结合图8 可知，对于带导向的深水数据，两算法水深误差在0～212.09 m，均值为9.23 m，约有77.4%误差分布在10.0 m 内，约13.0%数据误差大于20.0 m，且存在有极大误差的数据；中央波束误差与边缘波束误差均值分别约为1.39 m 和6.47 m，水深误差在10.0 m 内的数据占比分别约为99.2%和83.3%。由表8 可知，收发同体模型深度不符值中误差及均值远大于VCCA 模型，大于2%水深的超限点也进一步增多。对比本文2.2.1 节和2.2.2 节数据可知，随水深增加，姿态变化影响进一步明显并扩大，且在发射导向角的共同作用下，最终影响数据处理结果。

本文实测数据选用R2Sonic2024 和EM122 多波束系统采集数据，其标称测量结果符合IHO S-44特级精度要求，对应三组数据分别约为0.33 m、1.5 m、15 m。对比2.2 节可知，除无导向浅水区数据符合要求外，在发射导向和姿态的综合影响下，当水深大于200 m，存在部分数据超出标称精度要求的情况。

3 结论

本文从理论、模拟实验和实测数据三方面出发，对多波束Ping 周期内的姿态变化及其在发射导向角的共同作用下对测深点产生的影响进行了分析，结论如下。

（1） 姿态角度通过改变发射与接收时刻的波束能量来产生影响，其中，发射时刻纵摇、接收时刻横摇及两时刻的航向会对最终水深结果产生较大影响。

（2） 在单独考虑某一姿态角度变化下，横摇变化对水深结果的影响最大，且边缘波束受影响远大于中央波束，在横摇和发射导向的共同作用下，其水深相对误差可达到9.2%。

（3） 浅水环境下，对于集成安装的常规多波束测深仪（如R2Sonic2024、SeaBat7125 等）采集的数据，由于其Ping 率较高，姿态变化产生的影响可近似忽略，但当使用船体固定安装的深水或全海深型多波束进行浅水区作业、设备具有发射导向作用或水深相对较深（大于200 m）时应考虑其影响以得到更精细化的数据。

（4） 中深水及深水环境下，测量结果受姿态变化影响明显且迅速增大，此外，随着水深的增加和海况条件的影响，波束往返时间可达数秒甚至十数秒（特别对于深水或全海深型多波束系统，在不理想海况条件下千米水深Ping 周期也可能达十几秒），姿态变化明显的同时若存在发射导向角，则影响会更加明显，极易导致水深结果超出规范要求。

（5） 在数据采集过程中，应根据实际情况调整船速以及开角，当姿态变化明显时可适当降低船速，减小开角，以减少测点间距，同时保证航向和船艏向差别控制在小范围之内。