多源数据下的检测器布设及交通需求估计研究
陈 辉
(中交第二公路勘察设计研究院有限公司,江苏 南京 210012)
0 引言
交通需求是城市居民出行分布的集计,其准确性决定了城市交通规划与管理决策方案的科学性。当前城市交通系统可监测多源数据,这些多源数据给城市交通需求的准确估计带来了新的方向和挑战[1]。
近年来,学者们运用多种理论对交通需求进行估计。主要研究方法包括:广义最小二乘法[2]、指数平滑预测法[3]、贝叶斯估计方法[4]、基于公交卡数据预测法[5]、基于手机应用软件数据预测法[6]等。网络检测器布局问题作为交通需求的子问题,可以用来识别检测器布设位置,以确定唯一的未观测路段流量或者最优化待估交通需求的质量。为获得唯一的未观测路段流量,栾鑫等[7]利用成本和出行可靠性建立检测器布设模型;董春肖等[8]分析检测器布设位置对交通流量预测的影响;Fu等[9]提出多种类型检测器布设方案;Salari等[10]考虑检测器对交通需求估计的影响程度;孙超等[11]进一步提出了路径流量最大覆盖率准则。
尽管上述文献运用不同方法对检测器布局策略和交通需求估计进行了研究,但仍然存在一些不足:①已有文献没有使用多源数据融合技术进行交通需求估计。②对交通检测器布局的研究没有综合考虑路段和路径流量的覆盖信息。③缺乏从交通网络理论角度推导交通需求与流量之间的解析关系,该关系有助于建立最大似然交通需求估计模型。为此,该文提出检测器布局和最大似然交通需求估计整合模型。前者通过最大化路段和路径覆盖信息来计算最优检测器布局数量和位置,同时采用最小方差加权平均技术对检测的多源数据进行融合,从而运用最大似然法估计交通需求,并设计迭代算法求解模型。
1 检测器布设及交通需求估计
1.1 检测器布局模型
交通需求估计可被视为数学中的参数估计问题:观测部分样本(如道路流量、速度、密度、旅行时间等)来估计总体分布中的参数(即交通需求)。在既有预算下,观测哪些路段样本以估计出最可靠或最符合实际的交通需求,是该文需解决的前提性科学问题。
通过研究检测器布局模型来确定最优的检测器布设数量和位置,已有检测器布局模型单方面最大化路段覆盖信息或路径覆盖信息。该文在给定预算下,同时最大化路段和路径覆盖信息:
约束条件:
式中,W——路网OD对集;ω——其中的一个OD对;Kω——OD对ω之间所有路径的集合,k∈Kω;α——权重系数;——路段a上的先验流量;——OD对ω间路径k上的先验流量;——OD对ω间路径k上的覆盖系数,如果路径k上存在某个路段布设了检测器,该参数为1,否则为0;s——检测器数量;bs——检测器安装费用;bmax——总预算;za——路段a上的覆盖系数,如果路段a上布设了检测器,该参数为1,否则为0;A——路段集,a∈A;——在OD对ω间,如果路段a在路径k上,该参数为1,否则为0。
1.2 多源观测变量融合
观测检测器布设位置上的交通量、旅行时间、速度等数据,由于观测变量间的量纲不一致,采用交通流理论对观测变量间的量纲进行转换,从而统一化观测的多源路段信息。该文采用交通流三参数理论将多源观测变量统一为路段流量:
式中,va——路段a上的交通量;ta——路段a上估计的旅行时间;la——路段a的长度;Mj,a——路段a上的拥挤密度;Sf,a——路段a上最大行驶速度。
运用最小方差加权平均方法对多源数据进行融合:
1.3 最大似然交通需求估计模型
采用泊松分布描述随机交通需求qω:Pois(d ω),交通需求近似服从如下多元正态分布形式:
式中,d ——交通需求的均值向量形式,即d ={… ,dω,…}。该文假设交通需求之间相互独立,因此交通需求的协方差矩阵为 Λ= d iag (d)。在随机用户均衡模型中:
式中,——OD对ω间路径k上的流量;Pr(·)——概率算子;cω——路径旅行时间的向量形式,即对ω间路径k上出行用户路径选择概率:
式中,θ——出行者感知误差程度;——OD对ω间路径k上估计的路径旅行时间。因此路径流量也服从多元正态分布形式:
式中,V ——所有路段流量的向量形式,即V={… ,va,…},va——路段a上的交通流量;A表示路段集;Δ=()为路径 — 路段关联矩阵。
根据融合后的观测路段流量(式8)和路段流量与交通需求之间的解析关系(式13),建立交通需求的似然函数:
式中,g(·)——概率密度方程。由前面可知,路段流量V 的对数似然函数为:
基于融合技术,即式(8)获得的路段流量,运用双层规划理论建立最大似然交通需求估计模型,其中上层模型利用最大似然法求解交通需求,下层为SUE模型求解路径选择概率。
上层:
下层:用SUE模型(即式10)分配交通需求d,从而获得路径选择概率p 。
2 算法设计
在检测器布设过程中设计了逐次识别检测器算法,在求解最大似然交通需求估计模型时,运用迭代算法框架反复计算上层和下层模型。获得的检测器布设数量和位置,观测这些位置上的交通量、旅行时间、速度等,运用式(8)对这些观测变量进行融合,进而运用迭代算法估计交通需求。
步骤1 初始化:设置迭代步数n=0;收敛精度ε;交通需求的均值d(0),因此交通需求的协方差矩阵为Λ= d iag (d(0)),同时初始交通需求设为d(0);融合后的路段流量。
步骤2 求解下层模型:运用相继平均算法分配需求d(n),从而获得路径选择概率p(n)。
步骤3 求解上层模型:代入路径选择概率p(n),采用最速下降算法获得过渡交通需求。
3 算例分析
Nguyen-Dupuis城市路网[12]其拓扑结构、路段属性和交通需求量如图1、表1、表2所示,运用BRP函数来表示路段阻抗,其中ta——实际出行时间;——自由出行时间;xa——流量;Ca——通行能力;β=0.15和n=4为确定参数。
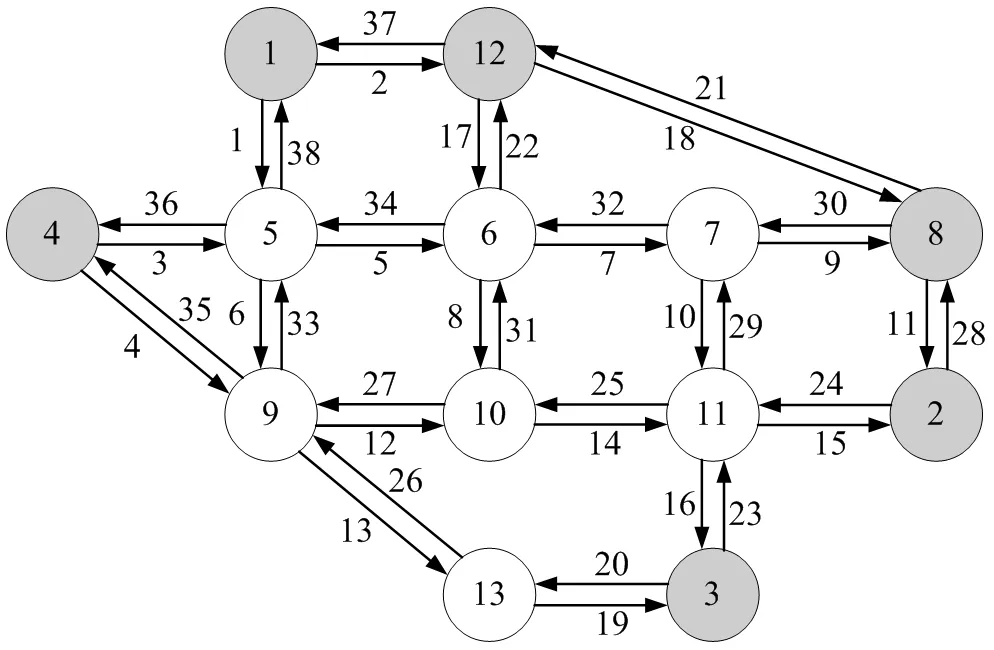
图1 Nguyen-Dupuis网络拓扑结构
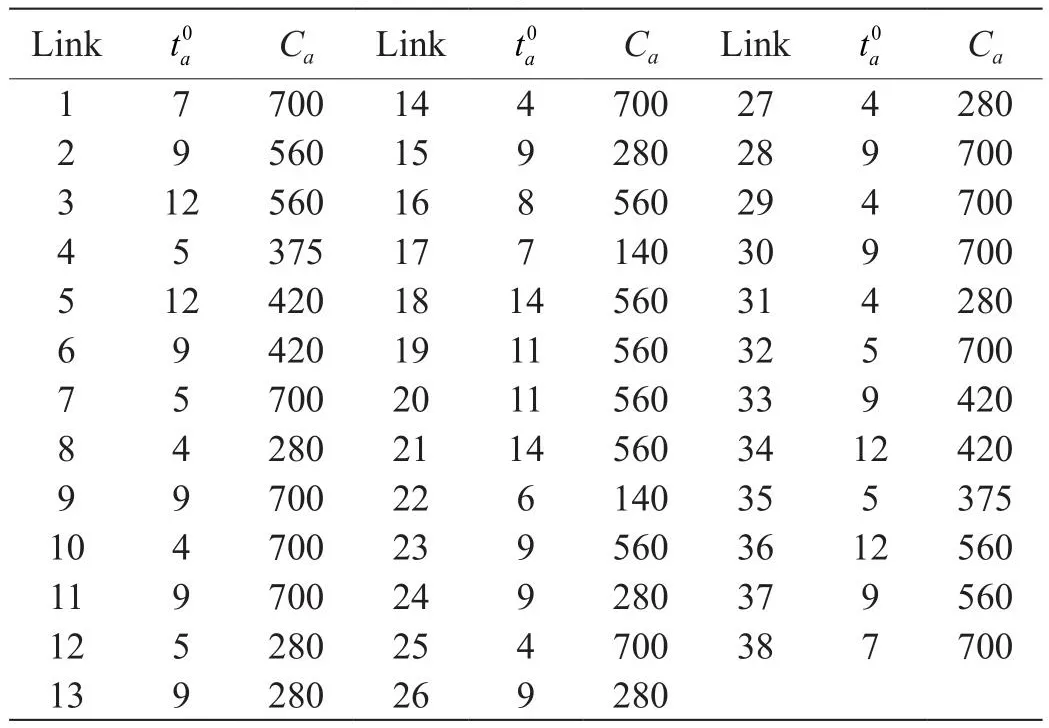
表1 Nguyen-Dupuis网络路段属性
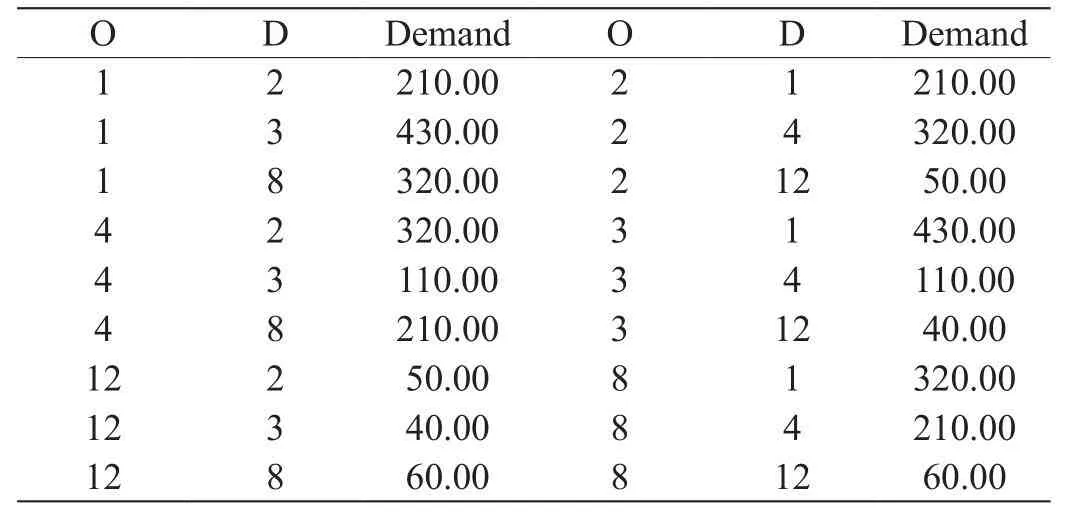
表2 Nguyen-Dupuis网络OD需求
权重系数设为α=0.5,路段检测器(路段速度)最大布设数量smax=6。图2描绘了随检测器布局位置逐一识别后,三种模型(目标函数仅考虑路段覆盖信息:;该文检测器布局模型;目标函数仅考虑路径覆盖信息:目标函数值的变化情况。从图中可以发现,三种模型下的目标函数值均随着检测器识别数量的增加而增加。与传统检测器布局模型相比,该文提出的检测器布局模型同时利用了路段和路径两方面的覆盖信息,可以获得可靠性更高的检测器布设方案。
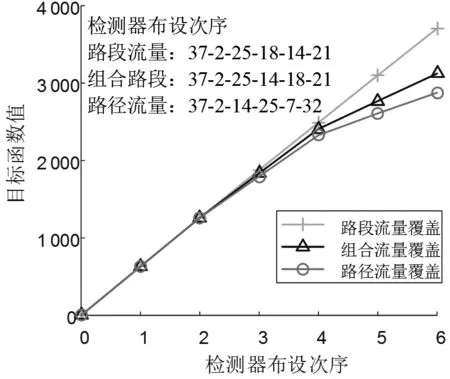
图2 目标函数值随检测器逐次识别变化图
根据图2中的检测器位置,观测路段37、2、25、14、18和21上的多源数据,其值为SUE模型分配交通需求均值所得,进一步根据式(8)对这些观测交通变量融合。从图3中可以发现当观测数据扰动都为0%时,交通需求的均方根误差接近0。且均方根误差随着观测数据扰动的增加而增大,这意味输入参数的扰动对交通需求的估计产生显著影响。
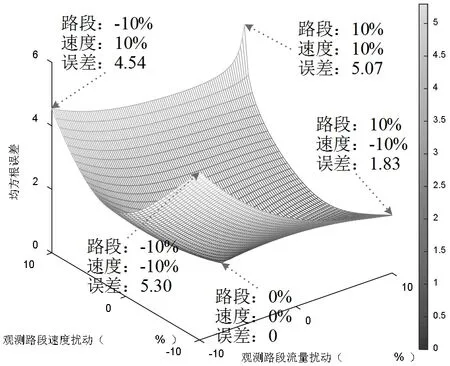
图3 观测数据对交通需求扰动分析
4 结语
为获取城市路网规划与交通管控的基础数据,利用现代信息技术观测的多源数据建立了检测器布局模型和最大似然交通需求估计模型,并设计了迭代算法求解建立的模型。
路网测试结果表明:同时考虑路段和路径两方面覆盖信息的检测器布局方案更具可靠性;输入参数的扰动对需求估计产生显著影响;设计的算法可以快速收敛于均衡解;多源数据融合下的交通需求估计方法通过充分挖掘观测数据信息,从而估计出与实际值相接近的交通需求。在后续研究中,将进行拥堵网络中动态交通需求估计,并进一步运用估计的交通需求对城市路网进行规划。

