宽转速范围下的航发主轴轴承故障诊断方法
张伟涛, 崔 丹, 刘 璐, 黄 菊
(1. 西安电子科技大学 电子工程学院, 西安 710071; 2. 中国航发贵阳发动机设计研究所, 贵阳 550081)
滚动轴承是旋转机械的重要组成部件之一,应用广泛。在旋转机械运行过程中,滚动轴承零部件会因众多原因出现不同程度的损伤,例如疲劳剥落、腐蚀磨损、塑性变形等。另外,滚动轴承在旋转机械中起连接作用,它的工作运转性能会随时间发生改变。由于滚动轴承在旋转机械中的核心地位,如果发生故障则会对机械设备造成灾难性的损害。对于旋转机械而言,30%的故障是由其核心部件轴承故障引起的。因此,轴承健康监测在现代工业中具有重要意义,而振动监测是预防灾难性损害最常见的手段之一[1-2]。
近年来,深度学习技术在图像和语音识别等领域都取得了巨大的成功,一些深度学习技术已经进入了机械健康监测系统[3]。目前机械健康监测主要是从振动信号的时域、频域和时频域三个方面与深度学习技术结合[4]。在时域方面,Zhang等[5]直接将原始振动信号作为卷积神经网络(convolution neural network, CNN)的输入,研究模型的抗噪性能。董绍江等[6]首先对原始振动信号采用SVD和EMD相结合的方法进行降噪,再通过卷积神经网络进行故障诊断。上述方法采用时域振动信号作为一维卷积神经网络的输入,而Lu等[7]将一维振动信号以时间序列重构后的二维矩阵与CNN结合应用于滚动轴承故障诊断,并验证了该方法在噪声环境下的鲁棒性。贺思艳等[8]利用时间序列构造二维样本,将其输入到卷积神经网络中进行故障诊断。利用时间序列构造的二维样本能够使网络提取信号相邻元素之间的特征。在时频域方面,刘炳集等[9]提出了一种基于时频图和CNN的滚动轴承故障诊断方法,在美国凯斯西储大学的公开数据集上能够达到97.63%的故障诊断正确率。Ma等[10]通过频率切片小波变换对原始振动信号进行时频分析,提出了TLCNN模型进行轴承故障诊断。肖雄等[11]提出了一种AMSGrad算法,用于二维卷积神经网络的优化,能够将故障诊断模型的诊断精度提高。上述方法虽然在故障诊断正确率上有一定的提高,但是仍存在较大的局限性,主要表现在如下两个方面。
(1) 现有的滚动轴承故障诊断方法大多数都是在美国凯斯西储大学的公开数据集上进行方法有效性及可行性的验证,然而该数据集的转速固定,仅包含30 Hz转频下的轴承振动信号,而航发主轴轴承正常工作时转速高达上万转,因此采用该数据集训练得到的网络模型并不适用于其它转速和载荷工况下的故障诊断,其应用具有很大的局限性。
(2) 轴承振动信号的采集对故障诊断起着至关重要的作用,现有方法使用的轴承振动信号均是在轴承座上采集得到的,然而这只是布置传感器的一种理想情况,实际情况下由于高温或机械结构的原因,传感器往往不能安装到轴承座上。因此,只能在发动机机匣或试验机保护壳体上采集振动信号,可能会导致振动信号故障特征不明显,故障诊断变得更加困难。
针对以上局限性,本文在振动信号采集,时频谱样本计算,以及故障分类神经网络构建等方面提出了新的方法。论文在航发轴承试验机上通过多个采集通道得到了几千组实验数据,实验数据对应的轴承转速和载荷范围分布广,更符合轴承故障诊断的实际情况。在时频谱样本表示方面,对原始的轴承振动信号先进行小波包重构,能消除振动信号采集过程中干扰分量的影响,使振动信号的故障特征更明显。在网络构建方面,通过跳跃连接建立具有深浅层特征融合特性的神经网络,可在网络参数量不变、计算量不增加的情况下,确保网络有足够的能力去处理更复杂的数据,解决转速时变、交变载荷工况下的轴承故障分类难题。
1 基于小波包重构的故障样本表示
1.1 轴承振动信号小波包重构
在实际工作过程中,轴承可能会由于润滑不良、载荷过大、异物侵入、锈蚀等原因,在轴承工作表面产生剥落、裂纹、腐蚀凹坑等缺陷。即使不出现上述故障情况,经过一段时间的运转,轴承也会出现疲劳剥落和磨损,最终导致轴承失效。其中,疲劳剥落是最常见的故障失效形式,主要是由于滚动体在内、外圈形成的滚道上承受交变载荷的作用,轴承使用到一定时间后,在接触表面会形成裂纹,随着不断的运转,裂纹会逐渐加深且面积逐渐增大,使得接触表面的金属呈片状脱落,形成缺陷。在轴承运转时,如果轴承的任一零件存在缺陷,滚动体不可避免的会与缺陷发生碰撞,产生冲击脉冲信号。该信号是典型的非平稳信号,且该冲击能量可能会引发轴承各零件的固有振动,成为与故障特征无关的干扰分量。
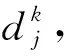

图1 3层小波包分解示意图Fig.1 Schematic diagram of three layer WPT decomposition
对于给定的轴承振动信号S(t),根据小波包变换可将S(t)利用小波系数重构为
(1)
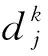
(2)
(3)
其中
(4)
式中:*表示共轭;〈·〉表示积分。至此,可通过式(3)实现小波包系数在相邻两层的递推求解。
论文在进行小波包变换时,选用Daubechies小波作为小波基函数,对轴承振动信号进行三层小波包分解,信号的总能量被分解到8个互不重叠的频率区间,然后计算第三层各节点小波包系数能量占该层总能量的比例
(5)

1.2 轴承振动信号时频分析
由于轴承振动信号的非平稳特性,使得时频分析成为轴承故障诊断的有力工具。论文采用最直观的短时傅里叶变换方法。短时傅里叶变换(short-time Fourier transform,STFT)的基本思想是采用固定长度的窗函数对时域信号进行截取并做傅里叶变换,得到时刻t附近很短时间段上的局部频谱。通过窗函数在整个时间轴上的平移,最终变换得到每一时间段上局部频谱的集合。基本变换公式如下

(6)
式中:f(t)为非平稳信号;g(t)为中心位于τ时刻的时间窗;STFTs(t,ω)大致反映了f(t)在t时刻,频率为ω“信号成分”的相对含量。
对于STFT,窗函数类型和窗口宽度是影响其变换效果的两个主要因素。选取合适的窗函数能有效减少频谱泄漏和谱间干扰。时频谱的相对分辨率会受窗口宽窄的影响,窗宽则频率分辨率高,窗窄则时间分辨率高。所以在对非平稳信号做STFT时,要根据信号特征合理的选择窗函数类型及其宽度。时频谱的频域和时域分辨率可由下列公式计算得到
(7)
(8)
P=F×T
(9)
P值大小决定了时频谱所包含的信息量。因此合理的F和T,能使时频谱包含的故障信息更加丰富,利于后期神经网络进行故障分类。
1.3 故障样本的时频表示
根据1.1节及1.2节的内容,首先对轴承振动信号进行小波包分解与重构,以达到消除采集过程中干扰分量的目的。然后,对重构后的信号做STFT,即可得到该振动信号的时频谱。基于小波包重构的故障样本计算如下(以轴承外圈故障振动信号为例):
步骤1轴承振动信号的采集。根据采集表,采集轴承在不同工况条件下五种故障状态的振动信号。
步骤2轴承振动信号的小波包分解。图2(a)是转速1 000 r/min,载荷4 kN的轴承外圈故障振动信号。将该振动信号进行三层小波包分解后,前5个分量重构后的信号如图2(b)所示。

(a) 轴承外圈故障振动信号
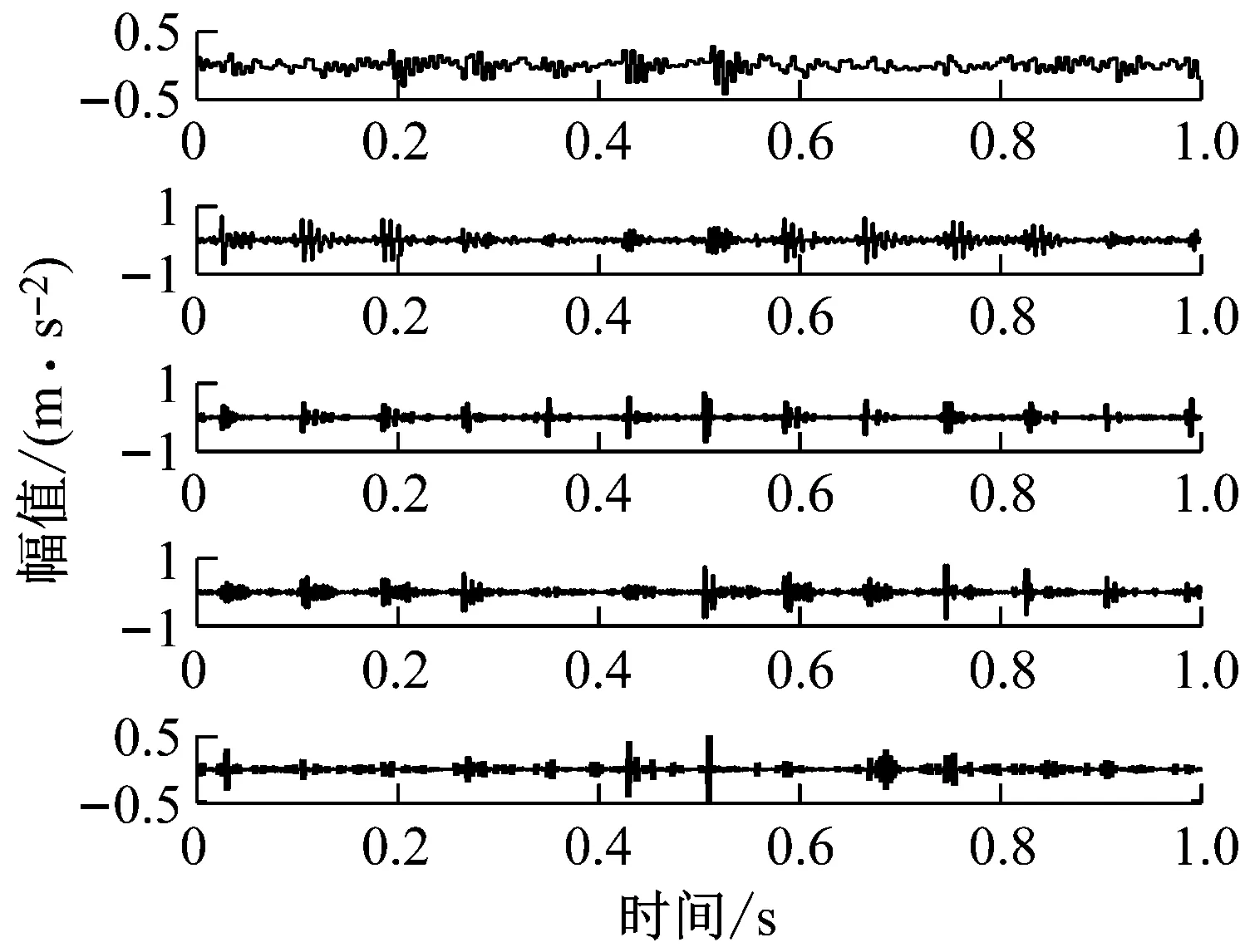
(b) WPT分解重构后前5个分量图2 轴承外圈故障振动信号的WPT分解与重构Fig.2 WPT decomposition and reconstruction of bearing outer fault vibration signal
步骤3有效故障信号分量的选择。由于轴承出现故障时会产生明显的冲击信号且容易被调制到高频共振带中,这些频段内通常包含着丰富的故障信息,论文通过计算小波包能量来选取有效故障信号分量以揭示故障信息。图3为轴承外圈故障振动信号WPT分解后第三层各节点的小波包能量值。

图3 第三层小波包能量值Fig.3 Energy value of third layer WPT decomposition
步骤4时频谱表示。将步骤3中获取的有效故障信号分量进行重构并做STFT计算,将各重构信号的STFT结果累加,即得到一个故障特征较为明显的时频谱样本,如图4所示。

(a) 滚动体

(b) 内圈

(c)外圈

(d) 正常图4 故障模式的时频谱Fig.4 TFR of bearing fault
2 深浅层特征融合网络训练与构建
卷积神经网络是一种前馈神经网络,近年来在图像识别和目标检测等方面有着出色的表现,能很好的处理过拟合问题,使更大规模的深度学习任务得以实现[12-13]。卷积神经网络通过改变相邻两层神经元之间的连接方式,引入权值共享,以达到降低网络参数量的目的,并以此来扩展网络结构。常用的基本单元有卷积层、池化层和全连接层。
2.1 故障分类网络的构建
论文中网络的输入是轴承故障振动信号的时频谱,经过深浅层特征融合神经网络进行故障特征提取及分类后,输出为故障类型,假设考虑的故障类型数为C。在实际工作环境中,由于交变载荷的影响,轴承中多个组件之间的相互作用具有时变特性,通常带有幅度、时间、频率等多个尺度的特征,基于单一尺度特征的故障分类网络难以有效地挖掘和利用其工作过程中数据所包含的多尺度信息。因此,论文提出新的网络架构以充分利用多尺度信息。
2.1.1 网络框架
论文提出的深浅层特征融合神经网络,结构如图5所示,主要由卷积层、残差模块、多尺度特征融合模块及全连接层组成。深浅层特征融合网络的特点在于残差模块和多尺度特征融合模块,模块中均使用跳跃连接。跳跃连接可使某个网络层激活后迅速反馈给另外一层甚至更深层,从而避免传统深度卷积神经网络在信息传递时产生的丢失和损耗问题。利用跳跃连接可以构建更深层的网络,在网络参数数量不变、计算量不增加的情况下,确保网络有足够的能力处理更复杂的数据。

图5 深浅层特征融合网络模型Fig.5 Deep and shallow feature fusion classification network
2.1.2 残差模块
有研究发现,随着构建的网络越深,网络越容易出现退化现象。残差连接能够有效解决网络退化的问题[14-15],论文采用的残差连接如图6所示。残差块包含两部分:直接映射和残差。网络某一层的输出通常可以看作y=H(x),而残差网络中一个残差块的输出可表示为H(x)=F(x)+x,F(x)表示残差块中卷积层的特征映射,残差即为预测值H(x)与观测值y=x的差值,F(x)=H(x)-x。所以残差网络的学习目标由H(x)变为F(x),网络只需要学习输入和输出差别的部分,从而降低学习难度。

图6 残差块示意图Fig.6 Residual block
残差块的输出为
xl+1=xl+F(xl,wl)
(10)
式中:xl+1为第l+1层的输出;xl为第l层的输入;F(xl,wl)为第l层的残差。
2.1.3 多尺度特征融合模块
论文中所采用的多尺度特征融合模块结构与残差模块基本一致,将残差块中两层特征图相加变为从深度上进行融合,具体如图5中的多尺度特征融合模块所示。卷积神经网络通过逐层抽象的方式来提取目标的特征。深层网络的目标特征信息表征能力强,但是特征图的分辨率较低,目标几何信息的表征能力弱。浅层网络的目标几何信息表征能力强,特征图的分辨率较高,但是其目标抽象表征能力弱。因此将深浅层特征图进行融合可以实现深浅层特征的优势互补,使网络同时挖掘到抽象的目标特征信息和高分辨率的目标几何信息,有利于提高网络的分类性能。
2.2 故障分类网络训练
深浅层特征融合网络的训练过程主要分为前向计算和基于误差反向传播的参数更新两部分。
2.2.1 网络前向计算
网络的前向计算过程主要分为三个部分:卷积层、批归一化层和全连接层,令网络的层数为L+1。
在卷积层上,用多个卷积核与输入时频谱样本进行卷积,加上偏置后通过激活函数即可得到一系列特征图,卷积过程表示为
(11)
(12)
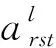

(13)
(14)
(15)
(16)

全连接层是将卷积层提取出的特征进行分类,其前向计算的过程为
(17)
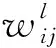
隐藏层激活函数为ReLU,即
a=f(z)=max{0,z}
(18)
式中:z表示激活函数的输入;a表示激活函数的输出。
输出层激活函数为Softmax,即
(19)
式中,qj为第j个神经元的输出。
2.2.2 基于误差反向传播的参数更新
对于一个具体的分类任务,网络训练的目标是使损失函数最小,因此选择一个合适的损失函数是十分重要的。论文采用交叉熵作为损失函数,其表达式为
(20)

在训练过程中,论文使用梯度下降法来最小化损失函数,以获得优化的参数。网络的参数更新公式为
(21)
式中,η为学习率,θ={w,b,γ,β}是网络所有待学习参数的集合。
2.2.2.1 全连接层参数梯度计算

(22)
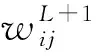
(23)
(24)

(25)
其中
(26)
(27)
(28)


(29)
(30)
至此,完成了全连接层参数的梯度计算。

(31)
令(r′,s′,t′)表示三阶张量神经元索引,则
p=(t′-1)RL-1SL-1+(s′-1)RL-1+r′
(32)
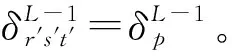
2.2.2.2 卷积与BN层参数的梯度计算

(33)
其中
(34)
(35)

(36)
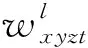
(37)
(38)
式中,x=0,…,n-1,y=0,…,n-1,z=0,…,Kl-1-1。
最后,计算损失函数E关于第l层中批归一化参数γ和β的导数
(39)
(40)
其中

(41)
至此,完成了网络中所有参数的梯度计算。
2.3 轴承故障诊断流程
基于深浅层特征融合的神经网络能够将信号预处理、故障特征提取和故障模式分类融合在一起,实现故障特征自适应提取及智能诊断,具体流程如图7所示。首先,对采集的轴承振动信号进行小波包重构成像,并将时频谱按工况条件进行划分,得到训练集和测试集。其次,将训练集输入到深浅层特征融合网络中进行参数学习,并利用梯度下降法更新网络的参数,直至网络的损失函数收敛为止,即可得到训练好的故障分类网络。最后,将训练好的网络模型应用于测试集,输出故障类型。

图7 基于深浅层特征融合网络的轴承故障诊断流程图Fig.7 Flowchart of bearing fault diagnosis based on deep and shallow feature fusion classification network
3 试验验证
3.1 数据集描述
试验共使用8个加速度传感器在SB25轴承试验机上采集轴承振动信号,采样率为20 kHz,轴承参数如表1所示。在轴承座外壳上布置了3个加速度传感器,如图8(a)所示,在试验机外壳上布置了5个加速度传感器,如图8(b)所示。共模拟了轴承的5种故障模式:正常、内圈缺陷、外圈缺陷、滚动体缺陷、保持架缺陷,模拟的缺陷情况如图9所示。

(a) 轴承座外壳

(b) 试验机外壳图8 传感器位置分布图Fig.8 Sensor location distribution

(a) 滚动体

(b) 外圈

(c) 保持架

(d) 内圈图9 四种故障模式Fig.9 Four bearing faults

表1 轴承尺寸参数Tab.1 Parameters of the bearing
试验采集的轴承振动信号转速范围:1 000~10 000 r/min,载荷范围:4~9 kN,共采集了5 568组数据,每组数据时长为10 s。论文将每个通道所采集的振动信号根据工况条件进行标记划分,得到每个通道的训练集和测试集,训练集共包含138种工况条件,测试集共包含135种工况条件,训练集和测试集的工况条件不同。将每个振动信号等分为100个样本,即每个通道的训练集共包含69 000个故障样本,测试集共包含67 500个故障样本。对每类故障标签采用“独热(one-hot)”的编码方式,即设置一个向量,其维数与故障类别数相同,除了某一位数字是1以外其余各维数字都是0。例如将正常状态的样本标签设置为4,则可编码成([0, 0, 0, 0, 1]),详细的数据描述如表2所示。

表2 试验数据集描述Tab.2 Experimental dataset
对重构后的轴承振动信号进行STFT,STFT的时间窗宽度为0.006 4 s(128个采样点),相邻两个时间窗重叠时间为0.004 95 s(99个采样点),傅里叶变换点数与窗口宽度一致,根据式(7)和(8)计算得到时频谱的分辨率为65×65,将分辨率修改为64×64,都圆整成2的倍数,能减少一定训练时间,且对最后的故障分类正确率影响不大。
3.2 试验结果分析
为了获取高精度的故障分类模型,需选取合适的超参数。在训练集上经过多次试验,最终将MiniBatchSize设置为100、学习率为0.001、MaxEpochs为10。
3.2.1 分类网络收敛特性
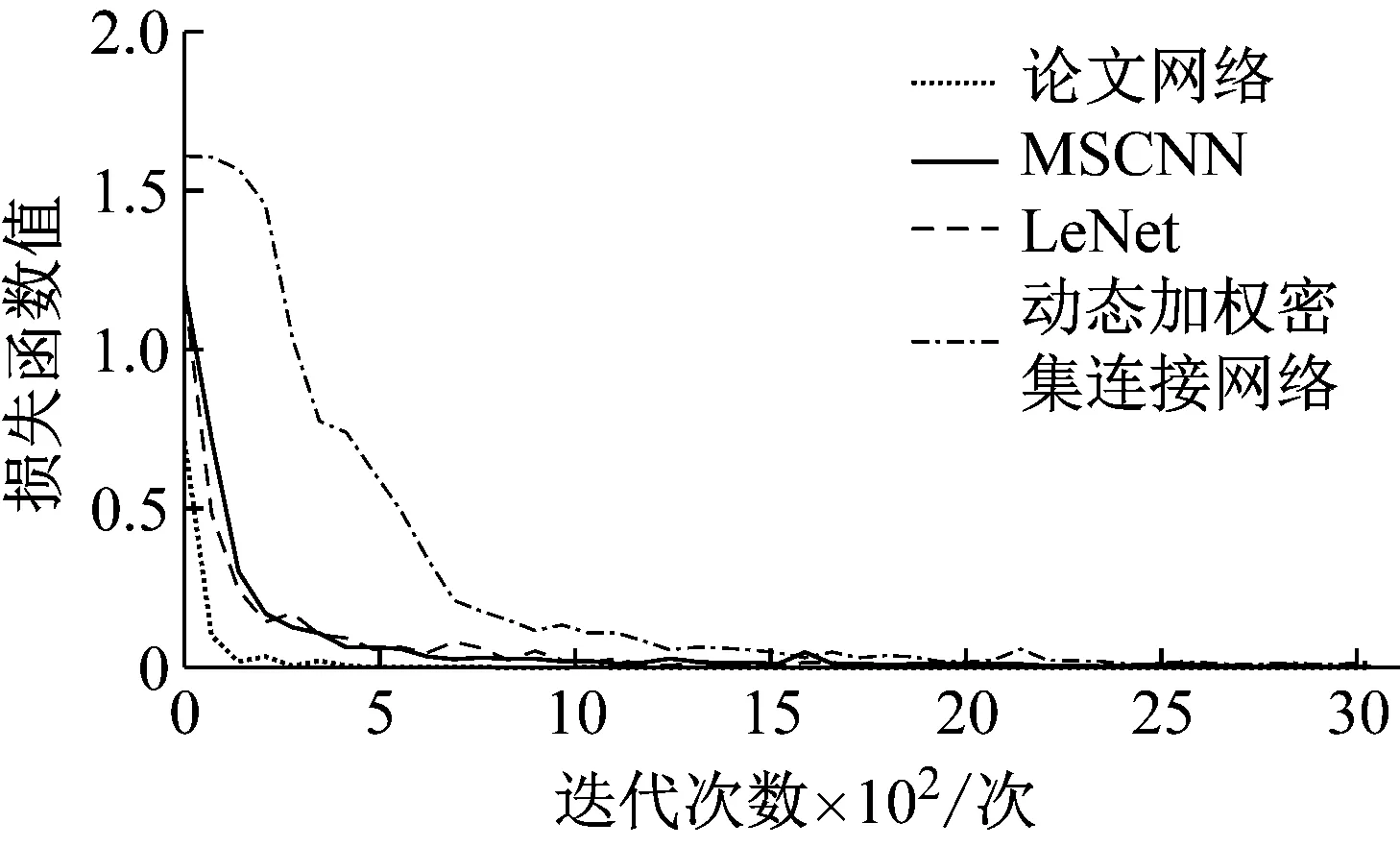
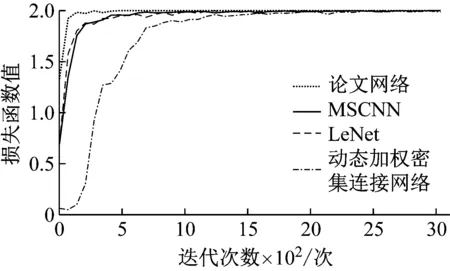
为了验证论文所提出的网络模型在转速时变、交变载荷工况下的收敛性能,与其他故障诊断方法所用的网络模型LeNet[17]、MSCNN[18]和动态加权密集连接网络[19]进行了对比,结果如图10所示。
(a) 损失函数下降曲线
(b) 故障识别正确率曲线图10 不同模型的收敛特性对比Fig.10 Comparison of convergence characteristics of different models
从图中可以看出论文所使用的深浅层特征融合网络故障分类正确率最高,且收敛过程稳定,收敛速度也有明显的提升,在迭代到第200次左右时,训练集上的故障分类正确率能达到100%。LeNet和MSCNN网络在迭代过程中会出现波动,动态加权密集连接网络的收敛速度最慢,稳定性最差。
3.2.2 不同时频分析方法性能对比
为验证短时傅里叶变换的优越性,与连续小波变换(continue wavelet transform,CWT)和魏格纳分布(wigner-ville distribution,WVD)进行对比。首先,将每个通道采集得到的振动信号经小波包重构,得到重构后的振动信号。其次,分别利用连续小波变换和魏格纳分布对每个通道重构后的信号进行时频分析,得到每个通道的训练集和测试集。然后,将不同时频分析方法得到的训练集输入到图5所示的网络中训练,得到训练好的模型。最后,将训练好的模型应用到对应的测试集上,输出故障分类结果。表3给出了采用不同时频分析方法与深浅层特征融合网络结合进行故障诊断的结果。

表3 利用不同时频分析方法后网络的分类结果Tab.3 The classification results of the network after using different time-frequency analysis methods
从表3中可以看出,经STFT处理后的数据集故障分类正确率最高。在通道0测试集上采用不同时频分析方法,STFT比CWT的故障分类正确率提高了3%,比WVD提高了6.2%。在通道2测试集上采用三种不同的时频分析方法,STFT比CWT的故障分类正确率提高了8.9%,比WVD提高了10.2%。由此可以验证,STFT方法在振动信号处理中的优越性,WVD由于交叉项的影响导致故障分类性能不佳。
3.2.3 网络分类性能测试
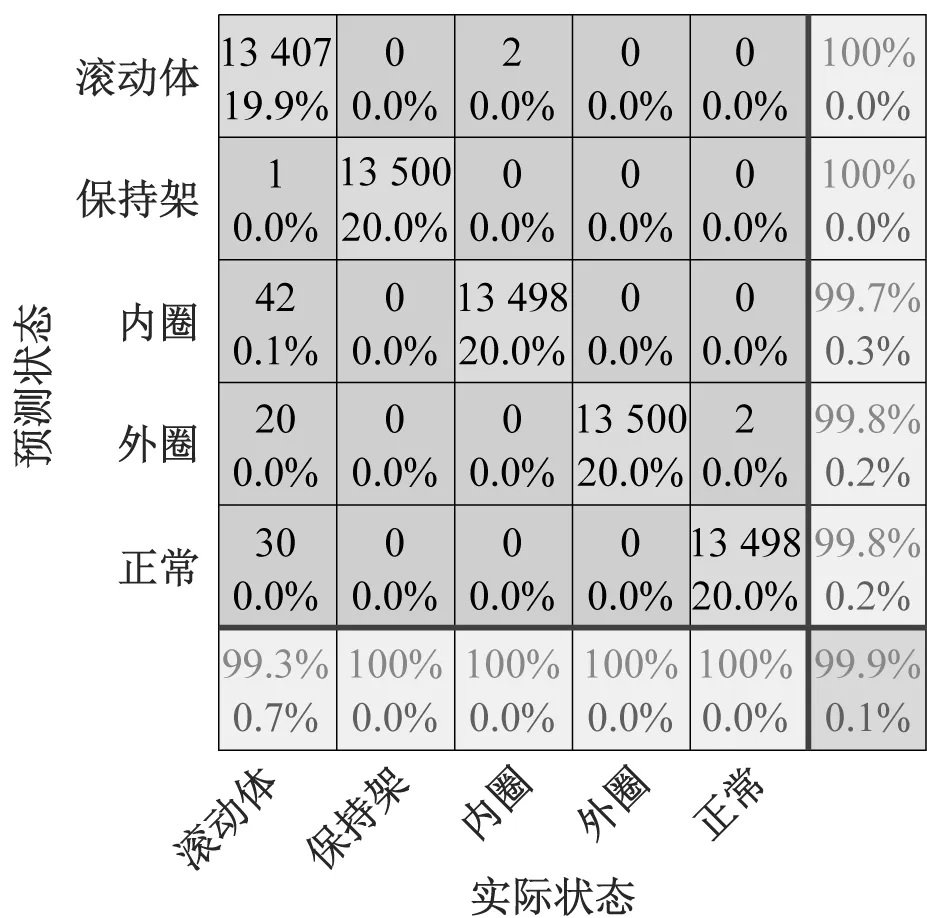
将八个通道的训练集分别输入到图5所示的深浅层特征融合网络中进行训练,将训练好的模型应用于测试集,得到八个通道的故障分类结果,在图11中给出了深浅层特征融合网络部分通道测试结果的混淆矩阵。并与LeNet、MSCNN和动态加权密集连接网络在相同数据集上进行分类性能的对比,对比结果如图12和表4所示。

(a) 通道0

(b) 通道1

(c) 通道2
(d) 通道7图11 部分通道测试结果的混淆矩阵Fig.11 Confusion matrix of partial channel test results

图12 不同网络结构的故障分类正确率Fig.12 Fault classification accuracy of different network
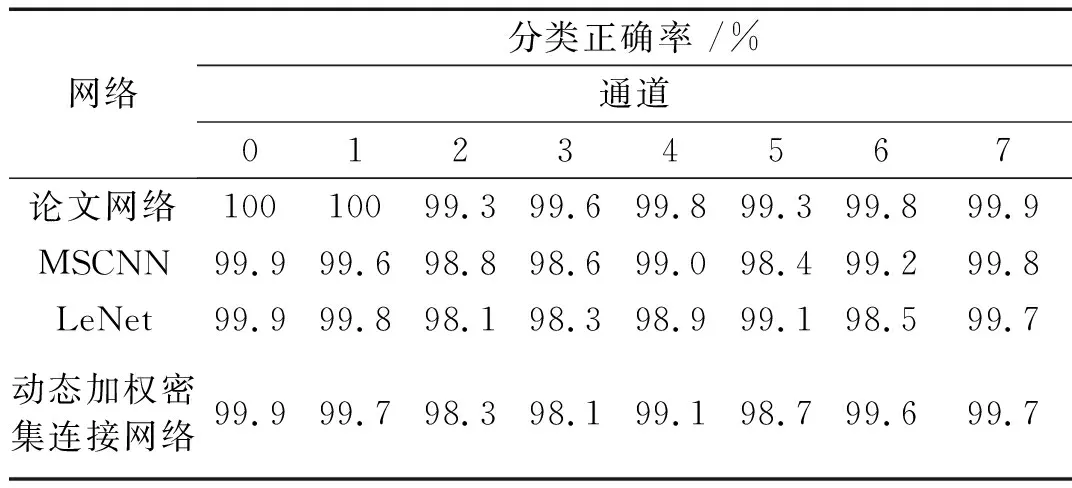
表4 八个通道测试集的识别正确率Tab.4 Accuracy of eight channel test sets
从图11中可以看出通道0、1和7对每种故障类型都能实现很高的故障分类正确率。从图11(c)通道2的混淆矩阵中可以看出,内圈故障一小部分样本会被错分为外圈故障,内圈故障的分类正确率为97.6%,其余故障的分类正确率均在99.7%以上。从两种故障类型的时频谱如图4(b)、(c)可以看出,两者的时频谱能量分布相似,所以在故障分类时容易产生混淆。
从图12和表4中可以看出,使用论文方法后通道0、1的故障分类正确率高达100%,且通道7的分类正确率也达到了99.9%,这是由于这三个通道相对应的传感器均放置在轴承座外壳上,相比放置在试验机外壳上的传感器,轴承座外壳处的传感器距离故障源更近,所以其对应传感器采集的振动信号故障特征最为明显,最有利于网络进行故障分类。传感器0、1水平放置在轴承座外壳上,而传感器7轴向吸附在轴承座外壳上,水平放置的传感器与轴承的振动方向基本一致,故其采集的振动信号相较于通道7更能揭示轴承的故障特征信息,所以其分类正确率能够达到100%。其余通道相对应的传感器均放置在试验机外壳上,距离故障源较远,所以故障分类正确率较低,但是也都达到了99.3%以上。
从表4可以看出,论文提出的网络模型在各个通道上的分类性能均优于其他模型,能够很好的识别不同故障类型,对于传感器3所采集的轴承振动信号,使用论文提出的网络模型相比LeNet能够将分类正确率从98.3%提高到99.6%,与MSCNN相比能够将分类正确率从98.6%提高到99.6%,相对于动态加权密集连接网络能够将分类正确率提高1.5%。而MSCNN与LeNet相比,由于其采用了多尺度网络模块,在大部分通道上其性能要优于LeNet。由此可见,多尺度模块能够挖掘数据的细节特征,提高网络的分类性能。而动态加权密集连接网络在分类层之前使用了全局平均池化,会导致丢失部分特征信息,对网络分类性能有所影响。经对比,验证了论文所提方法的有效性。
论文中的测试数据集共包含135种工况,图13为部分工况下八个通道的平均测试正确率,可以明显看出论文方法在高转速情况下故障分类正确率更高。在转速为9 100 r/min时,论文网络分类正确率为97.8%,而LeNet的分类正确率只有93.6%。在转速为8 500 r/min时,论文网络的分类正确率高达99.7%,相比其他三种网络分类正确率平均提高了3.4%。结果表明,论文网络在高转速情况下,能够很好的完成故障模式分类。
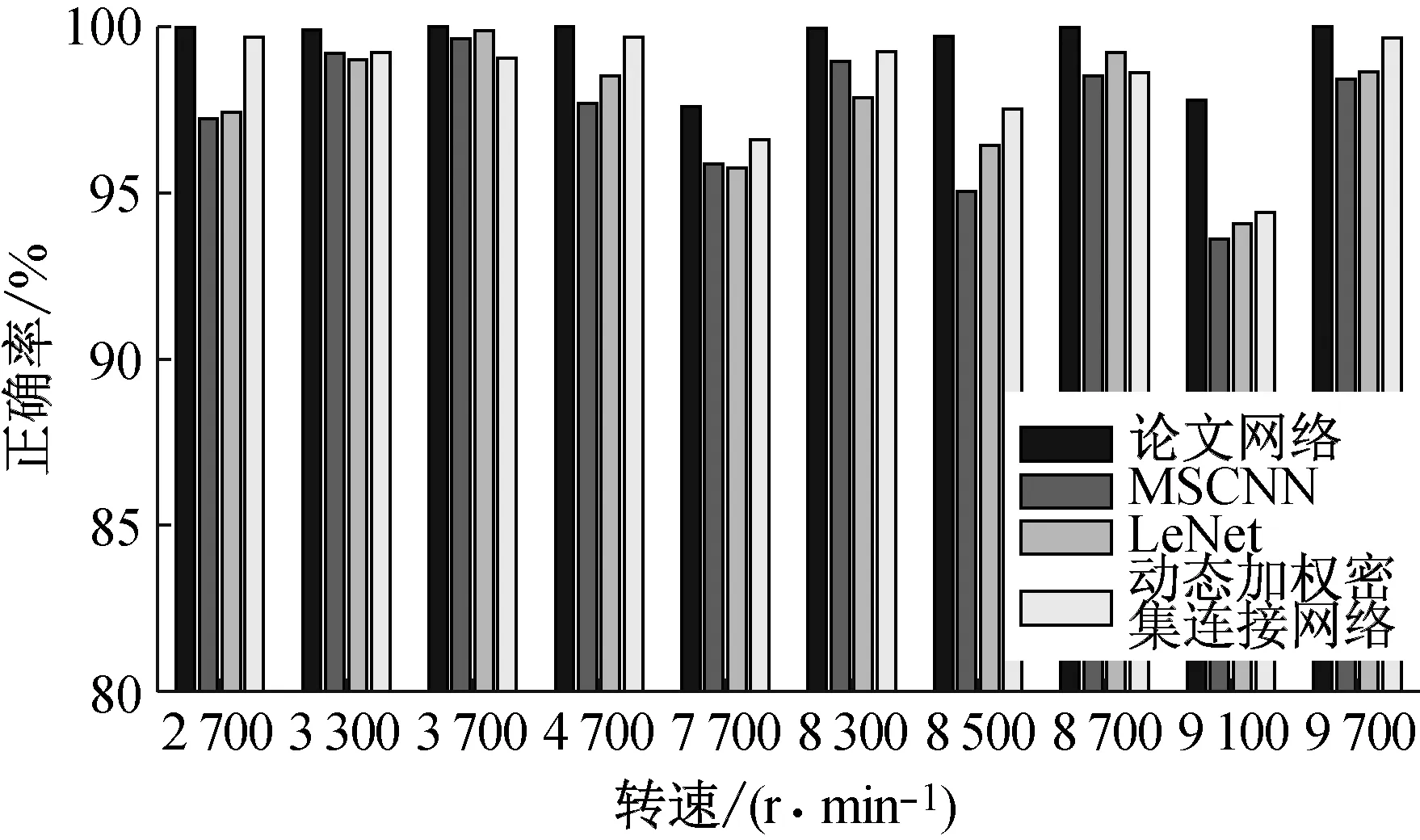
图13 部分转速下八个通道的平均测试正确率Fig.13 Average accuracy of eight channels at partial speeds
4 结 论
本文针对航空发动机主轴转速范围大导致的轴承故障诊断难题,提出了一种基于小波包重构成像与深浅层特征融合分类网络的故障诊断方法。首先,利用小波包分解提取滚动轴承振动信号中的有效成分,消除与故障特征无关的干扰分量。然后采用短时傅里叶变换对重构后的振动信号进行成像,得到时频谱样本。最后针对转速时变下的轴承故障分类问题,通过跳跃连接方式构建深浅层特征融合故障分类网络,实现对时频谱的特征提取,不仅降低了网络进行特征学习的难度,而且将浅层特征图的大量几何信息保留下来,与深层的特征图进行融合,提高了模型对输入的理解。相对于现有的轴承故障诊断方法,本文方法主要有以下优势:
(1) 构建的深浅层特征融合网络将特征提取与故障分类融为一体,对不同工况下的轴承故障在多个监测位置均有很好的诊断效果。
(2) 论文采集的轴承振动数据覆盖了更宽的转速范围,训练的网络能更好地胜任实际宽转速范围下的故障诊断需求。在训练集和测试集数据对应不同转速和载荷的情况下,网络的故障分类正确率依然能达到99%以上,泛化性能满足实际应用需要。

