超高层双子塔面对面与角对角布局的气动特性与抗风性能比较
秦玮峰, 杨肖悦, 石俊阳, 谢霁明
(浙江大学 建筑工程学院, 杭州 310058)
城市的快速发展和土地的稀缺,使得发展超高层建筑群成为一种趋势。其中,彼此相邻的双子塔是一种常见的建筑形式。一些双塔建筑已成为所在城市的新地标,例如307 m高的昆明西山双子塔与406 m高的贵阳花果园双子塔等。
矩形超高层双子塔设计中面对面与角对角是两种常见的布局方式,各有优点。例如上述的昆明西山双子塔是典型的面对面布局,而贵阳花果园双子塔则是典型的角对角布局。在概念设计阶段,面对面与角对角是两种常见的可选方案。由于风效应是超高层建筑设计中需要重点考虑的因素,选择对抗风较为有利的布局方式有助于提高设计的合理性与项目的经济性。但目前尚未见到比较明确的研究成果。
根据已有的研究结果[1],面对面双塔最不利的风向角分别为并联方向与串联方向,而角对角双塔最不利的风向角主要为斜角方向与串联方向。因此面对面与角对角布局的双塔在气动特性与抗风性能方面的差异是显而易见的。
国内外对高层建筑的干扰效应已开展了大量研究[2-4],主要分为两大类。第一类关注施扰建筑对受扰建筑的气动干扰,谢壮宁等[5-8]对双方柱在不同间距、不同高宽比、不同风场等参数下的干扰效应做了系列研究,得到了一系列线性拟合公式。这类研究的目的主要是为了评估周围建筑群对单独建筑物的风场影响。第二类关注双塔间的相互干扰,主要目的在于把握双子塔结构的气动性能并用于抗风设计。本文涉及的气动干扰问题属于这一类。
杜晓庆等[9]发现串列的面对面双塔的气动力相关性和立面风压的非高斯区域对双塔间距的变化十分敏感。石俊阳等[10]从时域和频域的角度研究了不同间距下面对面双塔气动力的相关性,发现主要呈负相关。Xie等[11]发现连体结构会导致双塔间的风荷载重新分布,串列的面对面双塔主要呈反相位运动。Song等[12-13]研究了面对面双塔层间风力系数的相关性以及双塔基底荷载的相关性。杜晓庆等[14]和Kim等[15]分别利用大涡模拟和粒子图像技术分析了串列双塔周围的流动状态及其对气动干扰的影响,探究了气动力系数相关性随双塔间距的变化规律。
目前双子塔气动特性研究主要针对面对面布局,相比而言针对角对角布局的研究则很少。Du等[16]研究了均匀流场下角对角双塔的气动力的风向特性,发现角对角双塔的气动特性与面对面双塔有显著不同。陈强等[17]研究了角对角布局双塔的局部体型系数和整体体型系数,提出采用角对角布局能够最大程度保证围护结构安全。Ni等[18]研究了角对角双塔与面对面双塔的平均气动力,发现角对角双塔的平均阻力系数小于面对面双塔。这些研究成果集中于对体型系数(或阻力系数)的讨论,但有关角对角双塔风致响应的研究尚未见到,无法满足超高层双子塔的工程需求。
为满足工程设计的实际需求,本文采用风洞试验方法对面对面与角对角两种布局下的双子塔的气动特性与抗风性能进行了对比研究。首先比较了两种布局方式的双塔在不同间距下的气动特性,然后以风振加速度与基底总荷载作为指标评估两种布局方式在不同设计条件下的相对优劣。所得结果可为双子塔的抗风设计方案优选提供技术参考。
1 比较研究方法
1.1 风洞试验方案设计
研究对象由两栋完全相同的方形超高层塔楼组成,塔楼的足尺高度为300 m,长度和宽度均为45 m。模型缩尺比取为1:300,相应的风洞试验模型高度为1 m,参见图1。风洞试验的采样频率为312.5 Hz,采样时长90 s。试验在浙江大学ZD-1边界层风洞实验室完成。

(a) 面对面布局双子塔

(b) 角对角布局双子塔图1 双子塔的同步测压模型Fig.1 Pressure models of twin towers
在风洞试验中,每座塔楼表面共布置240个测点,分为6个测点层,每层布置40个测点,两座塔楼共480个测点进行同步测压,典型层的测点布置见图2。为了提高测压点随高度的分布密度,在两栋楼上还另外设置了间距较近的6层共480个同步测压点,用于检验数据处理时测点加密技术的效果。

图2 典型层测点布置Fig.2 Layout of pressure taps on a typical floor
风洞试验的坐标系与风向角的定义如图3所示,其中左边定义为T1塔楼,右边定义为T2塔楼。从满足工程设计的实际需求考虑,统一采用各塔的结构坐标系统。
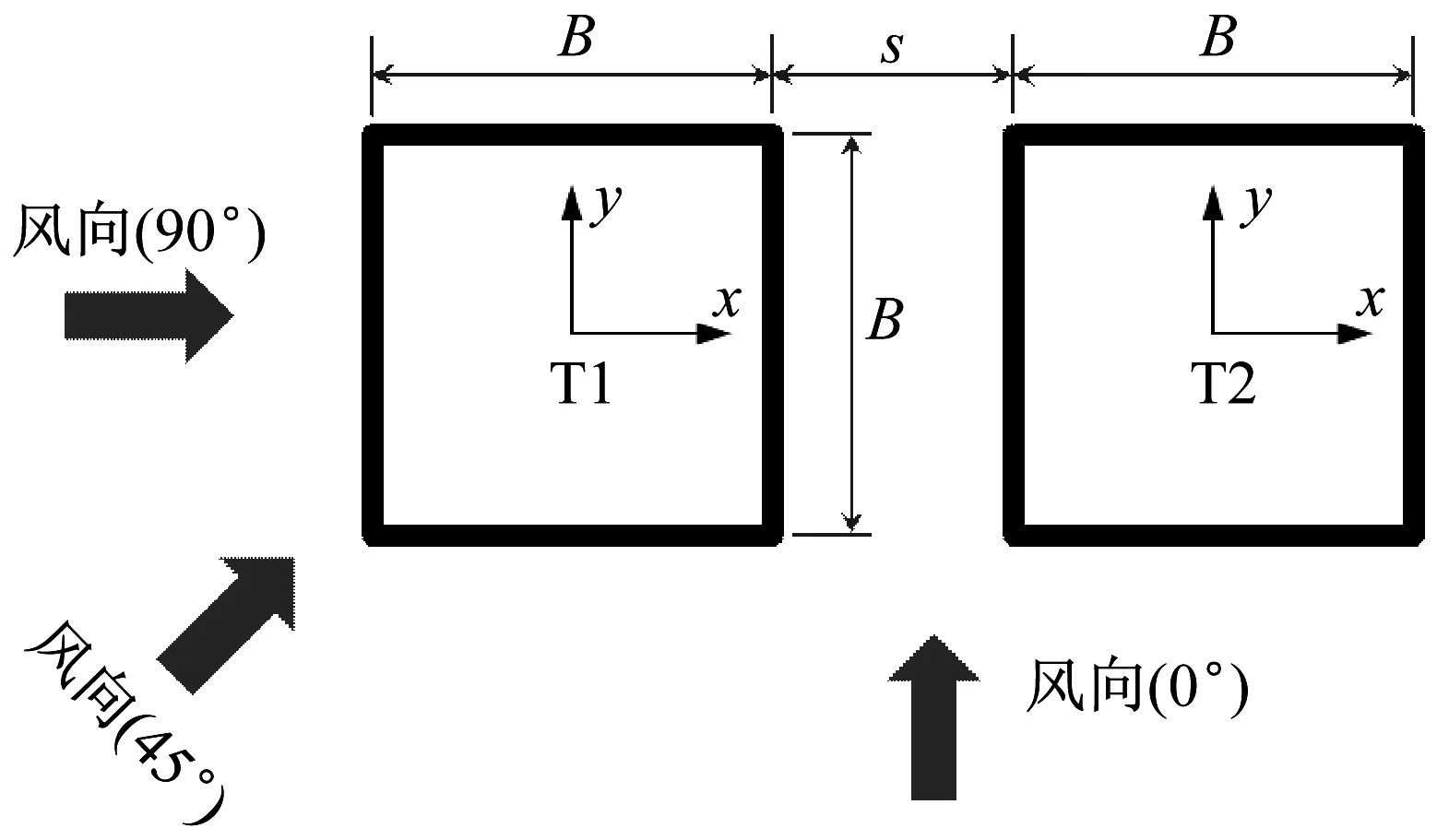
(a) 面对面布局双子塔

(b) 角对角布局双子塔图3 坐标系与风向角的定义Fig.3 Definition of coordinates and wind directions
根据以往的研究成果,面对面双塔的最不利风向角比较固定,分别为串联和并联方向(即0°和90°)。而角对角双塔的最不利风向角则分别出现在串联方向与对角线方向附近(即45°和90°附近),同时两栋塔上最不利的风向角略有差别。为此,除了测试0°、45°和90°风向角外,对角对角布局的双塔增加测试了45°和90°附近的风向角。
为方便表达,采用符号s/B(s为双塔间距,B为单塔的建筑宽度)来表示双塔相对间距。根据实际超高层双子塔常见的间距范围,设置了s/B为0.25、0.5、0.75、1.0、1.25、1.5、1.75、2.0一共8个不同的相对间距。此外作为参考,对其中一栋塔楼进行了单塔试验。
1.2 流场设置
风洞试验采用指数率风剖面,利用尖劈、粗糙元等模拟了地貌粗糙度指数0.15、缩尺比1∶300的B类地貌风场,参考点高度为1 m(=楼顶高度),参考点风速为10.8 m/s,1 m高度处的湍流度约为9%。图4为风洞平均风速剖面、湍流度剖面以及模型楼顶高度处的脉动风速功率谱。其中H0表示楼顶高度;U0表示楼顶高度平均风速;Iu表示湍流度。换算成足尺后的湍流积分尺度Lu为160 m。风洞试验的雷诺数为1.1×105,阻塞比小于5%。
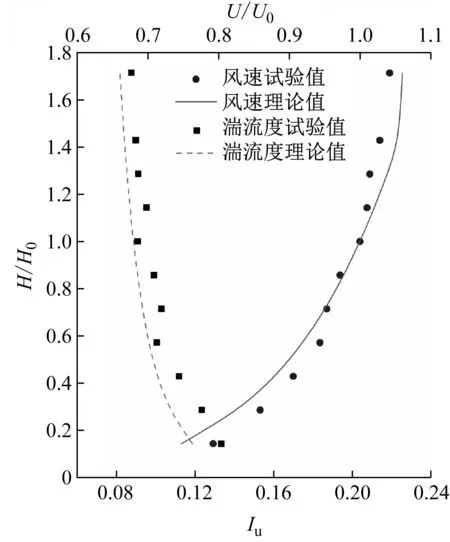
(a) 平均风速剖面与湍流度剖面

(b) 顺风向脉动风速功率谱图4 模拟的B类地貌风场参数Fig.4 Simulated wind parameters in terrain B
1.3 试验数据的分析方法
通过压力积分,计算出结构的整体气动力系数时程,包括基底剪力系数、基底倾覆力矩系数以及广义气动力系数。具体计算公式如下
基底剪力系数
(1)
基底倾覆力矩系数
(2)
广义气动力系数
(3)
式中:p(t)为模型表面的风压时程;dA表示与风压测点对应的参与面积,取与系数计算方向一致的的投影面积;z表示离基底的高度;Φj表示第j阶模态振型函数,本文研究中考虑沿x方向与沿y方向侧向振动的两阶基本模态;ρ表示空气密度,取ρ=1.25 kg/m3;UH为楼顶高度的参考风速;B和H分别为建筑的宽度和高度。
在求算式(1)~(3)的积分中,为了提高离散测压点的分辨率,采用本征正交分解(POD)方法进行测点加密处理[19-22]。这一方法保证了表面随机风压场的基本相关结构,其结果的准确性可通过加密层测点获得检验。由于相关的技术细节不是本文的主要内容,以下省略对这一方法的详细讨论。
将结构的运动方程以广义坐标的形式表达,结构风致响应可通过求解下列运动方程得到。
j=x,y
(4)
式中:ηj(t)为广义位移;ζ为结构阻尼比;ωj为对应模态的自振圆频率(ωj=2πfj);Pj为广义气动力;mj为广义质量。
为提高求解运动方程的可靠性,对式(4)分别进行了频域分析与时域分析以相互检验。采用频域分析时,第j阶广义加速度的均方根值可由下式得到
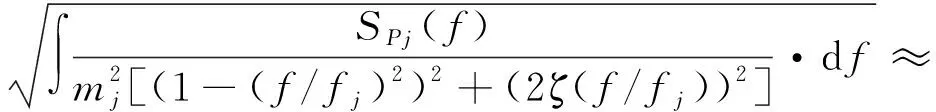
(5)
式中,SPj(f)为广义气动力的功率谱。
时域分析采用四阶Runge-Kutta法。根据相似原理,广义气动力时程的步长由下式确定
(6)
式中:λL为风洞试验模型的几何缩尺(λL=300),κ为风洞测压数据采样频率(κ=312.5 Hz);UH.Model为模型高度的风洞试验参考风速(UH.Model=10.8 m/s);UH.Full为相应建筑高度的足尺风速。
由频域分析与时域分析得到的结构风振的均方值响应基本一致,而时域分析结果可进一步用于检验基于高斯过程的峰值系数假定。因此,后续的结果展示全部基于时域法的计算结果。
风振响应计算中取结构自振周期8 s,结构阻尼比2%,典型结构层高4 m,楼层质量2 500 t,基本振型近似为(z/H)1.25。
为了使所得风振响应具有一般性意义,按抖振理论将结构响应进行如下无量纲约化处理。
约化加速度
(7)
用于结构设计的风荷载中应包括平均荷载、背景脉动荷载以及由风致振动导致的惯性荷载。因此可以采用包含这三个荷载分量的基底总荷载(即基底剪力与倾覆力矩)作为评估角对角双塔与面对面双塔抗风性能的指标。类似地,可以将基底总荷载以无量纲约化的形式表达。
约化基底剪力

j=x,y
(8)
约化倾覆力矩

j=x,y
(9)


(10)
式中:μ为标高z处的楼层质量;g为峰值系数。
2 不同间距下气动特性的比较
2.1 平均气动力的比较
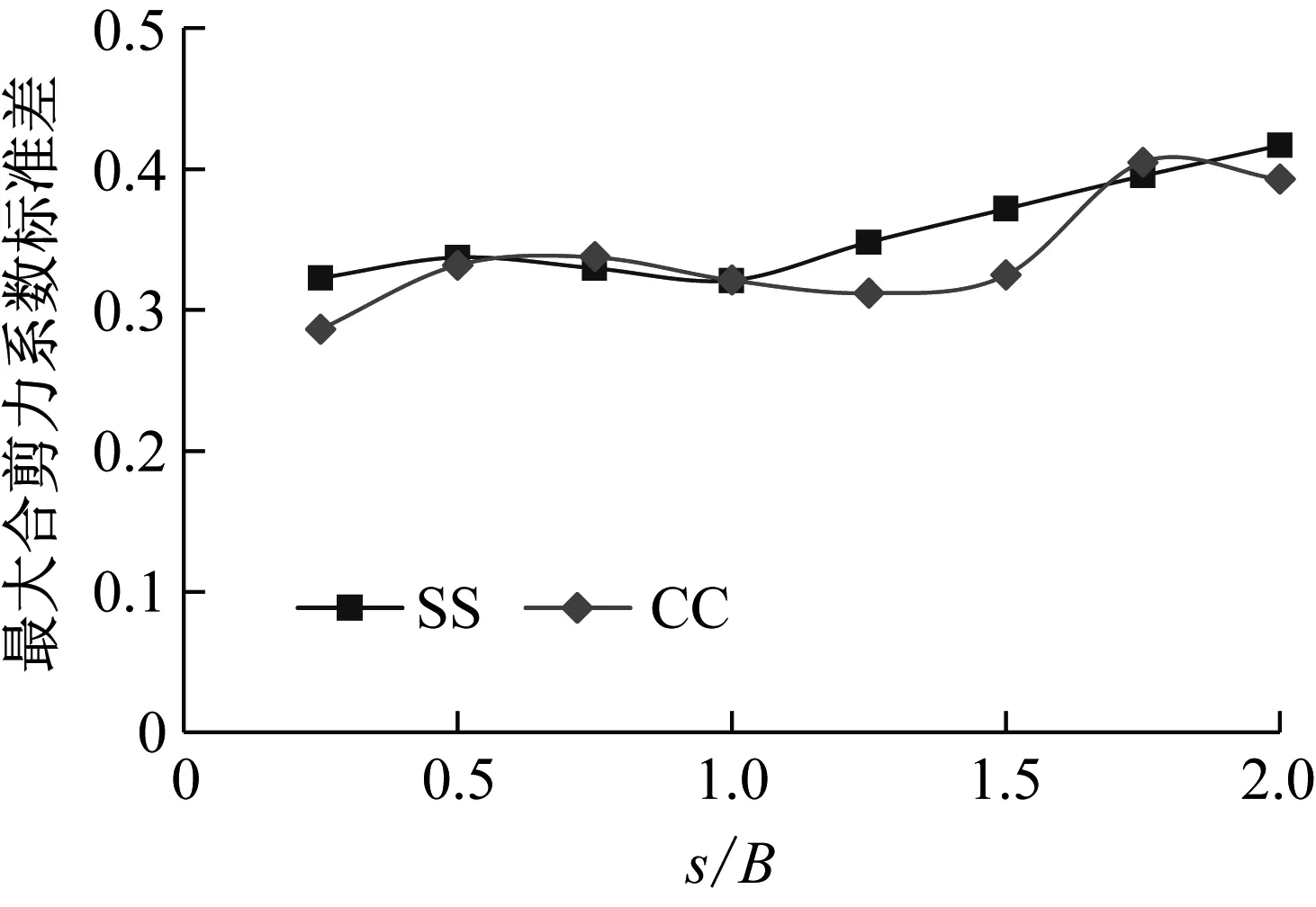
图5给出了在三个典型风向角下,面对面双塔与角对角双塔的合剪力系数平均值随双塔间距s/B的变化。图例中SS(side-by-side)代表面对面双塔,CC(corner-to-corner)代表角对角双塔。合剪力系数定义为x方向与y方向剪力系数的矢量和,主要由气动力的阻力作用组成。

(a)T1塔楼的合剪力系数平均值
在90°风向角下,T2塔楼受到上游T1塔楼的“遮挡效应”,面对面或角对角布局的双塔合平均气动力都大幅减小,这与谢壮宁等的结论一致。
考虑到实际工程项目中,双子塔中任一栋塔楼都可能成为上游塔或下游塔。因此从比较面对面与角对角布局的气动特性优劣而言,应当比较在所有风向角下两栋塔楼中的最大气动力数值。图6给出了这一结果。可以看出,当仅仅关心最大平均风荷载时,面对面布局与角对角布局在数值上并没有显著的区别。

(a)所有风向下双塔最大合剪力系数平均值
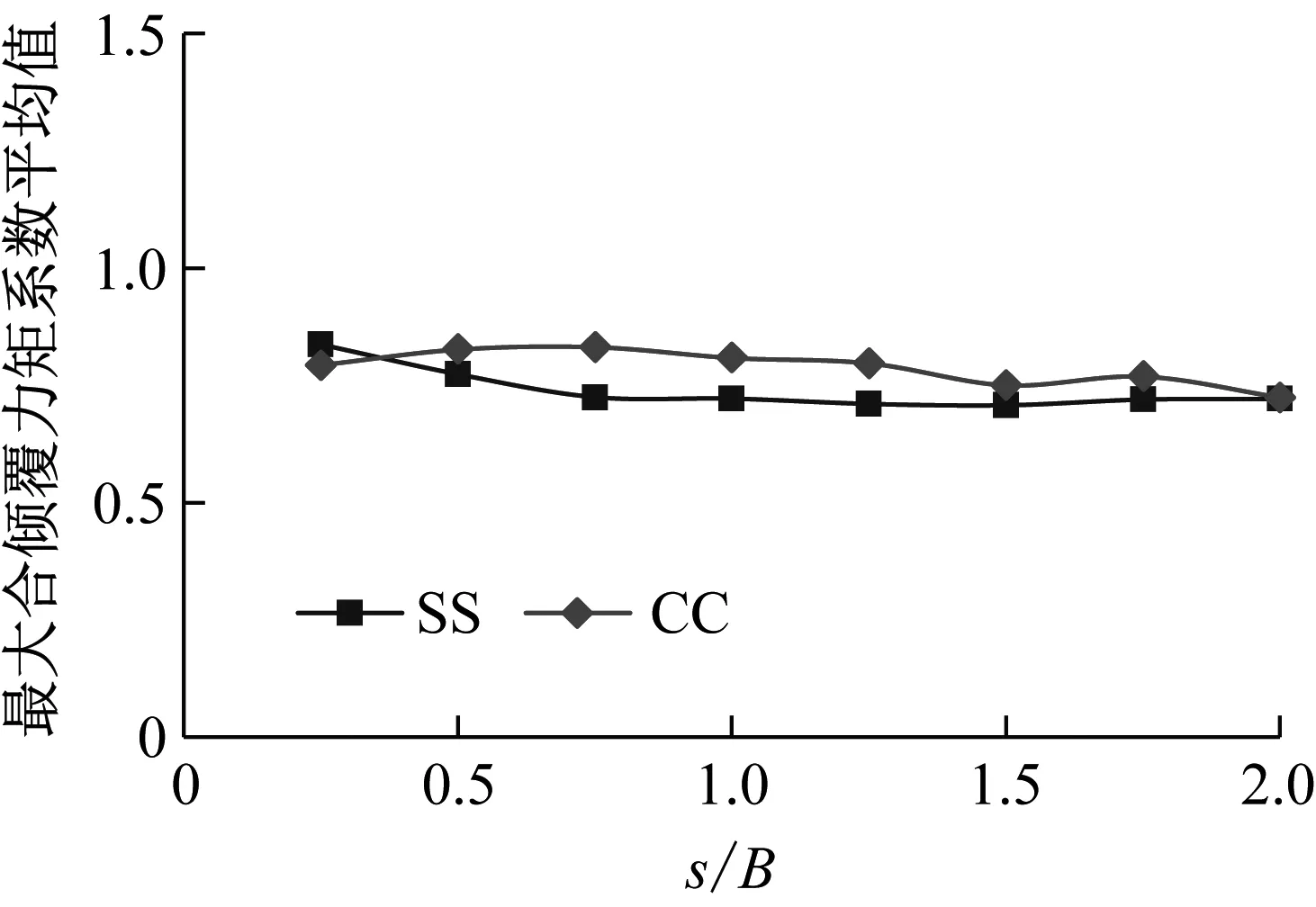
(b)所有风向下双塔最大合倾覆力矩系数平均值图6 最大平均气动力比较Fig.6 Comparisonofmaximumstaticforcecoefficients
2.2 脉动气动力的比较
图7给出代表气动力脉动分量的合剪力系数标准差随双塔间距的变化。可以看出,对于上游塔(T1),面对面布局的最大合剪力系数标准差依据双塔间距不同分别出现在0°与90°风向角下,而角对角布局的最大合剪力系数标准差则始终出现在45°风向角附近,并且在数值上明显小于面对面布局。对于下游塔(T2),面对面布局的最大合剪力系数标准差仍然出现在0°与90°风向角下,而角对角布局的最大合剪力系数标准差则依据双塔间距不同分别出现在45°与90°风向角下。就最大值而言,面对面布局与角对角布局对下游塔气动力脉动分量的影响不大。

(a)T1塔楼的合剪力系数标准差

(b)T2塔楼的合剪力系数标准差图7 脉动气动力系数的标准差Fig.7 Standarddeviationsoffluctuatingforcecoefficients
类似地,由图8可以看出当仅仅关心最大脉动标准差时,面对面布局与角对角布局在数值上并没有显著区别。
(a)所有风向下双塔最大合剪力系数标准差

(b)所有风向下双塔最大合倾覆力矩系数标准差图8 最大脉动气动力比较Fig.8 Comparisonofmaximumfluctuatingforcecoefficients
2.3 气动力的频谱特性比较
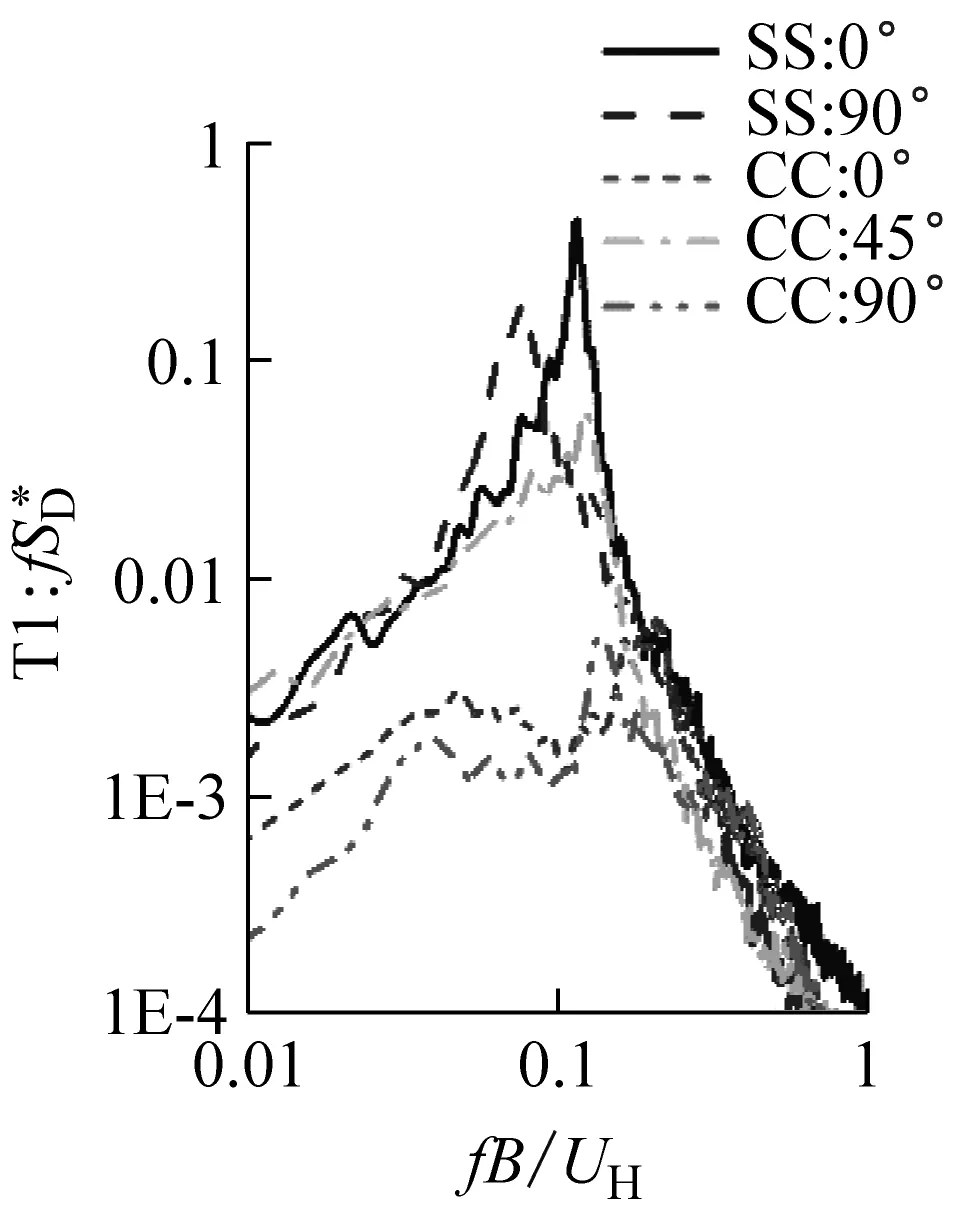
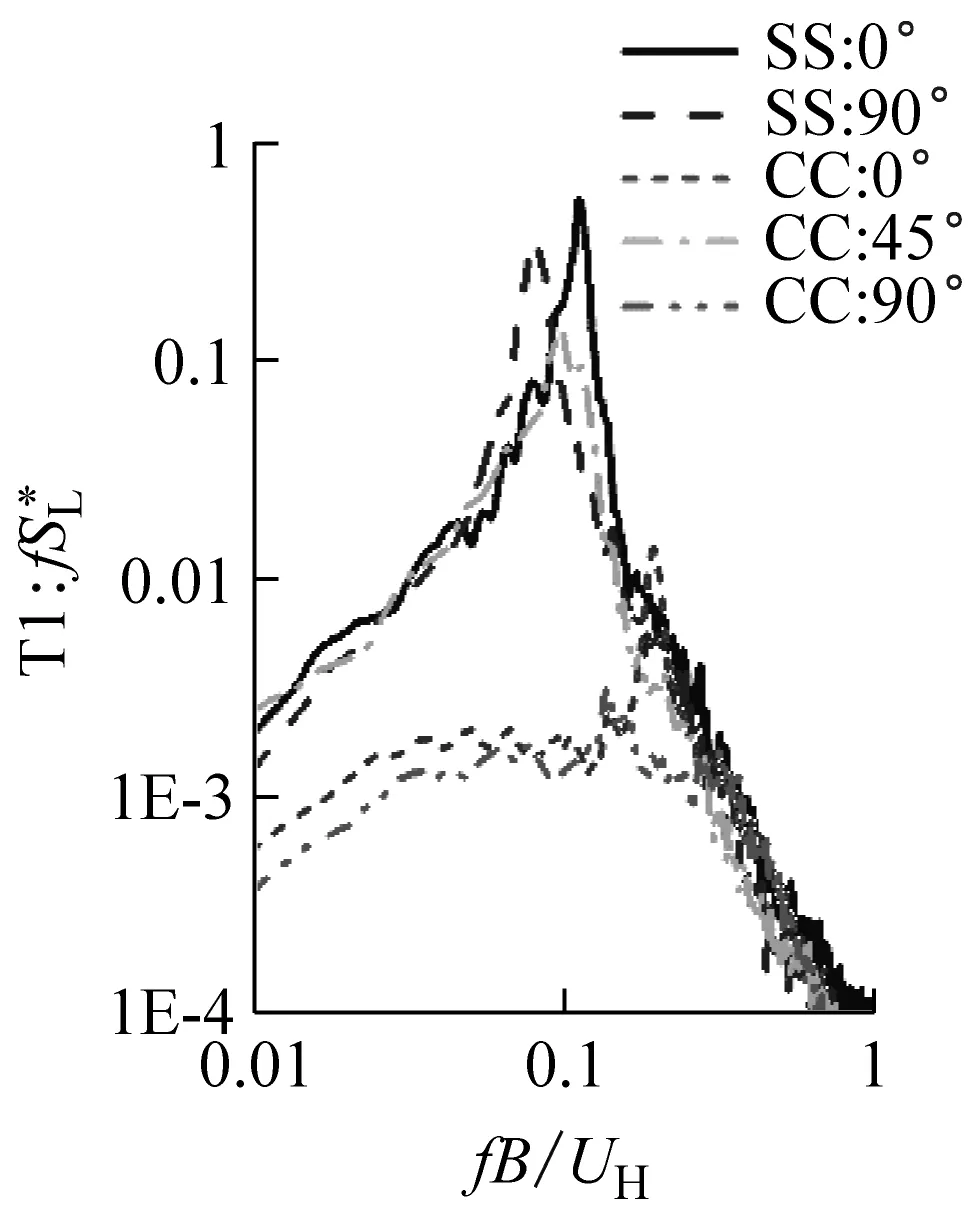
在评估结构的风振响应时,除了需要考虑气动力的脉动分量标准差大小外,还必须考虑脉动分量的频谱特性。气动力中的顺风向分量与横风向分量的产生机理有所不同,因此频谱特性也非常不同。为了从原理上对面对面双塔与角对角双塔在气动力频谱特性上进行比较,宜采用风向坐标,即顺风向坐标(记作D—阻力方向)和横风向坐标(记作L—升力方向)。选取面对面布局与角对角布局中最不利的典型风向角进行比较:
对比一,进行0°风向角时的面对面布局与45°和0°风向角下的角对角布局的对比。0°风向角时面对面布局下,顺风向气动力沿Y轴,而横风向气动力沿X轴;45°风向角时角对角布局下,顺风向气动力沿X轴,而横风向气动力沿Y轴;0°风向角时角对角布局下,顺风向和横风向气动力均与X轴和Y轴成45°夹角。
对比二,进行90°风向角时的面对面布局与同样90°风向角下的角对角布局的对比。90°风向角时面对面布局下,顺风向气动力沿X轴,而横风向气动力沿Y轴;90°风向角时角对角布局下,顺风向和横风向气动力均与X轴和Y轴成45°夹角。
这个事例说明了延迟满足法的局限性,自控力是内化的能力,就像它的名字一样,是“自己主动去控制”,而我们使用延迟满足法时,其实是用外在力量影响孩子。靠外力实现的自控,短期内有一定效果,但肯定不如孩子主动控制好。
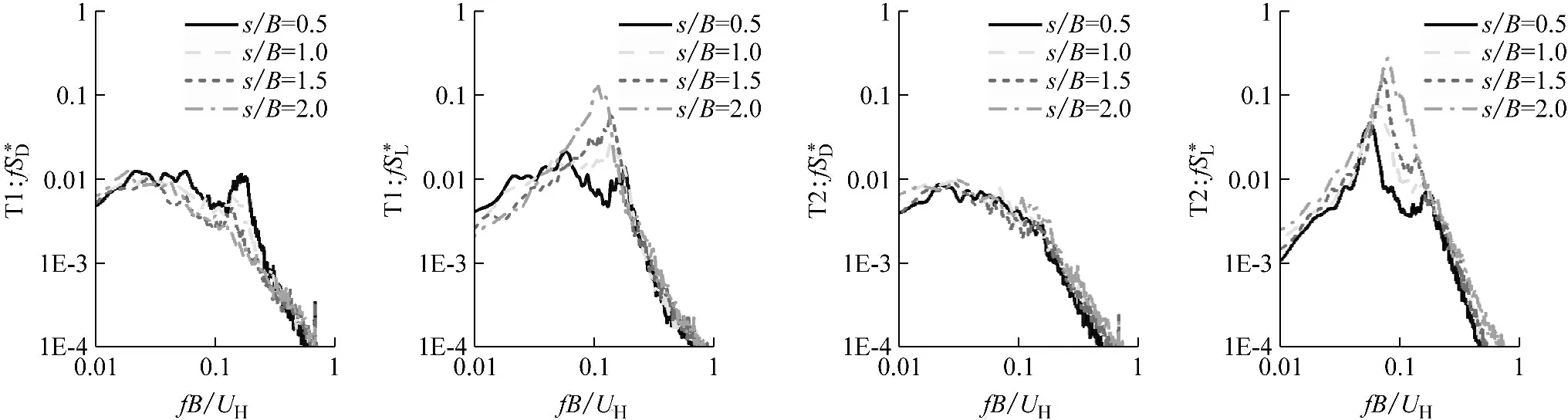
在4个典型间距(s/B=0.5、1.0、1.5和2.0)下两种布局的气动力功率谱分别见图9和图10。图9为对比一,重点考察两种布局下的横风向涡激气动力。图10为对比二,重点考察两种布局下的尾流激振力。

(a)面对面布局:0°风向角
(b) 角对角布局:45°风向角

(c) 角对角布局:0°风向角图9 面对面与角对角双塔的气动力功率谱对比一Fig.9 Comparison of spectra of force coefficients

(a) 面对面布局:90°风向角

(b)角对角布局:90°风向角图10 面对面与角对角双塔的气动力功率谱对比二Fig.10 Comparisonofspectraofforcecoefficients
由图9可见,虽然两种布局下横风向气动力功率谱的涡激峰值都随着双塔间距的减少而降低,但在类似间距下角对角布局45°风向角的功率谱峰值明显低于面对面布局。这表明在角对角布局下,即使双塔间距较大时也存在较大的双塔气动干扰作用(T2塔楼位于T1塔楼的左后方),从而影响并抑制了规律性的旋涡脱落。而在角对角布局0°风向角时,塔楼的气动外形较优,因此横风向涡激气动力始终很小。由此可见,就横风向涡激气动力而言,角对角布局优于面对面布局。
图10表明,面对面布局在90°风向角时上下游的塔楼都会受到较大的横风向气动力作用,气动力的大小随双塔间距的增加而增大。在双塔间距较小时,上游塔横风向气动力大于下游塔。随着双塔间距的增大,上下游塔楼的横风向气动力大小趋于接近。与此相比,角对角布局在90°风向角下的上游塔横风向气动力始终很小,但在下游塔上却观测到由尾流产生的数值很大的横风向气动力,其能量非常集中。而且间距越小,尾流激振力越大。由此可见,在角对角布局的双子塔抗风设计中需要对尾流激振问题予以特别关注。
为了更清楚地考察不同间距对两种布局下的气动特性差异的影响,图11按间距大小给出横风向气动力谱的比较。
由图11可以看出,当仅考虑最不利风向角时,所有间距下角对角布局的上游塔上的横风向气动力基本上均小于同样间距下的面对面布局。然而下游塔的情况则比较复杂。

(a)s/B=0.5,T1塔楼

(b)s/B=1.0,T1塔楼
(c)s/B=1.5,T1塔楼
(d)s/B=2.0,T1塔楼
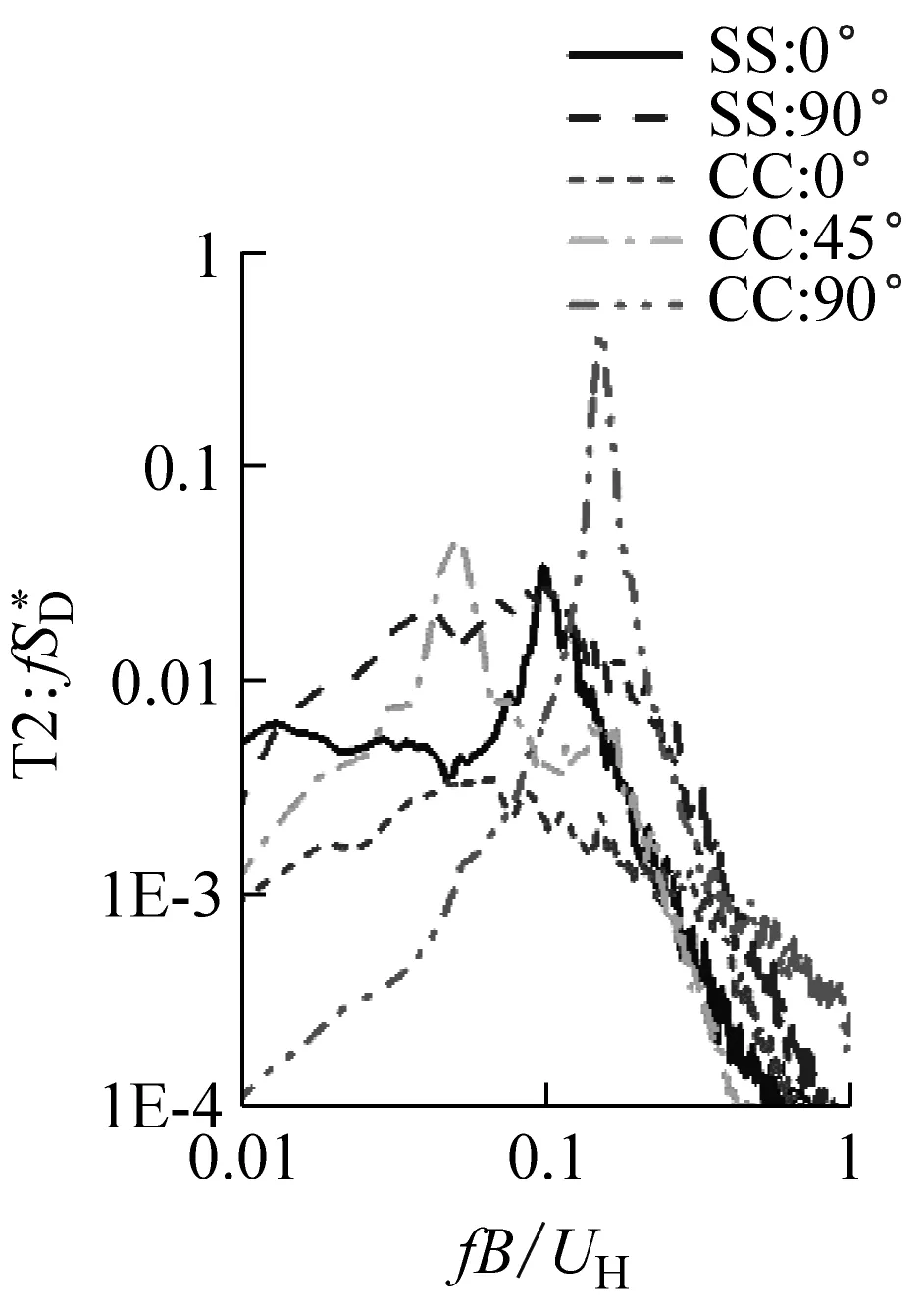
(e)s/B=0.5,T2塔楼

(f)s/B=1.0,T2塔楼

(g)s/B=1.5,T2塔楼
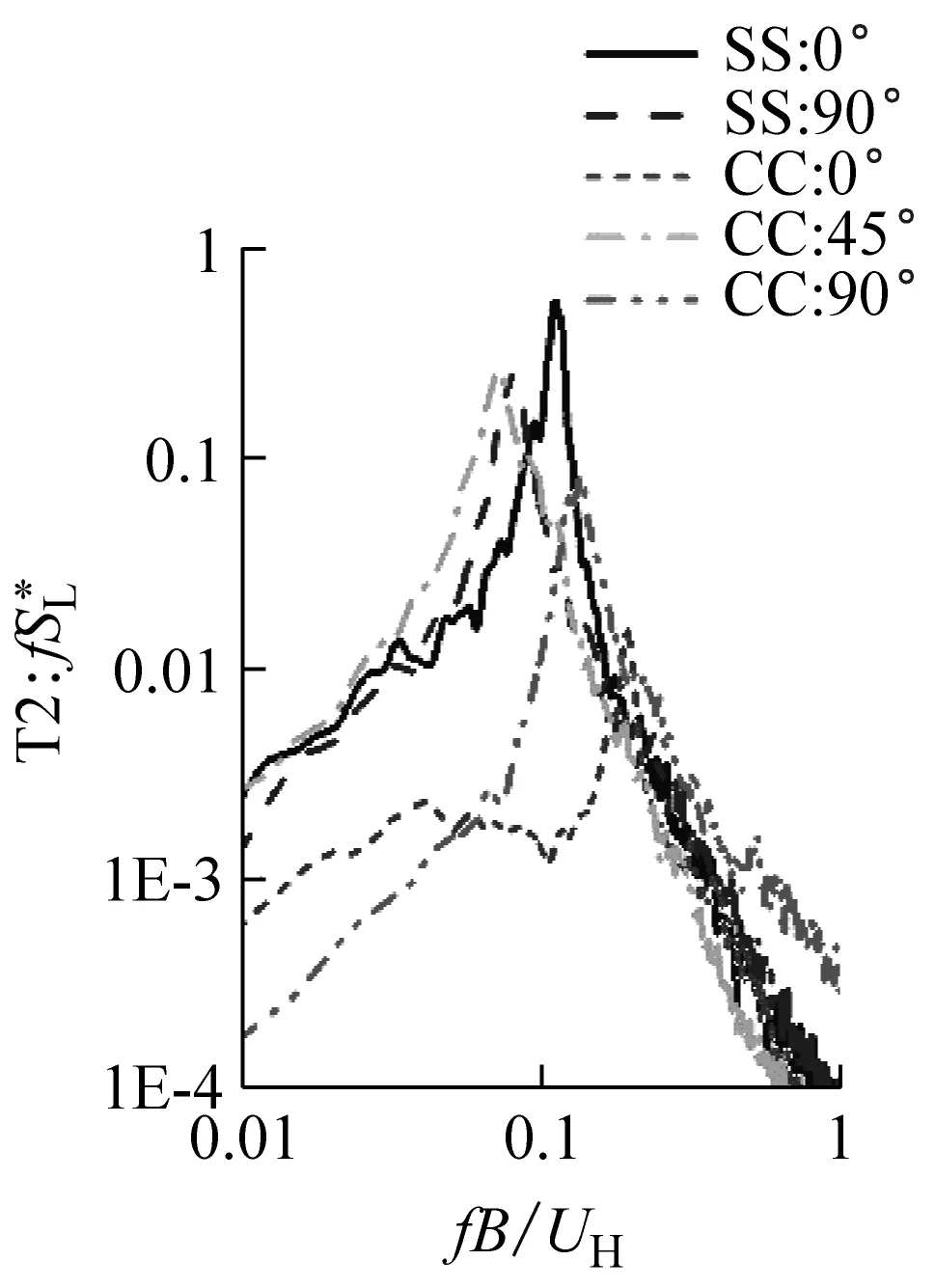
(h)s/B=2.0,T2塔楼图11 横风向气动力功率谱随间距的变化Fig.11 Variationofacross-windspectrawithspacing
在小间距时(s/B≤0.5),双塔间的气动干扰比较强烈,使得两种布局下的涡激力都受到有效地抑制。但尾流激励会使得角对角布局时下游塔受到能量非常集中的尾流激励,横向气动力大大高于面对面布局的情况。
在中等间距时(s/B=1.0),面对面布局和角对角布局的涡激气动力峰值比较接近,但两者的卓越频率(最大谱值对应的频率)并不相同。面对面布局的卓越频率在0.12附近,角对角布局的卓越频率在0.08附近。这说明角对角布局的涡激临界风速高于面对面布局。在这一间距下尾流激励仍然较大,但幅值已有所下降。
在大间距时(s/B处于1.5~2.0),角对角布局的横向气动力峰值小于面对面布局,同时峰值对应的临界风速也高于面对面布局。并且角对角布局的尾流激振力得到进一步削弱,其幅值已低于涡激气动力。
不同间距下的比较结果说明面对面和角对角布局所导致的气动力差异主要表现在频谱特性方面,而气动力平均值的差异其实很小。所以仅从体型系数是不能揭示这两种布局在风振响应与抗风性能方面的真正区别。而且对超高层双子塔,风振响应大小是评估抗风性能的主要指标。
3 不同间距下的结构风致响应比较
3.1 风振加速度的比较
在不同风向角下,上游塔和下游塔的风振加速度是非常不同的。图12所示为双塔间距为1.0时两种布局下按式(7)得到的楼顶风振加速度标准差。
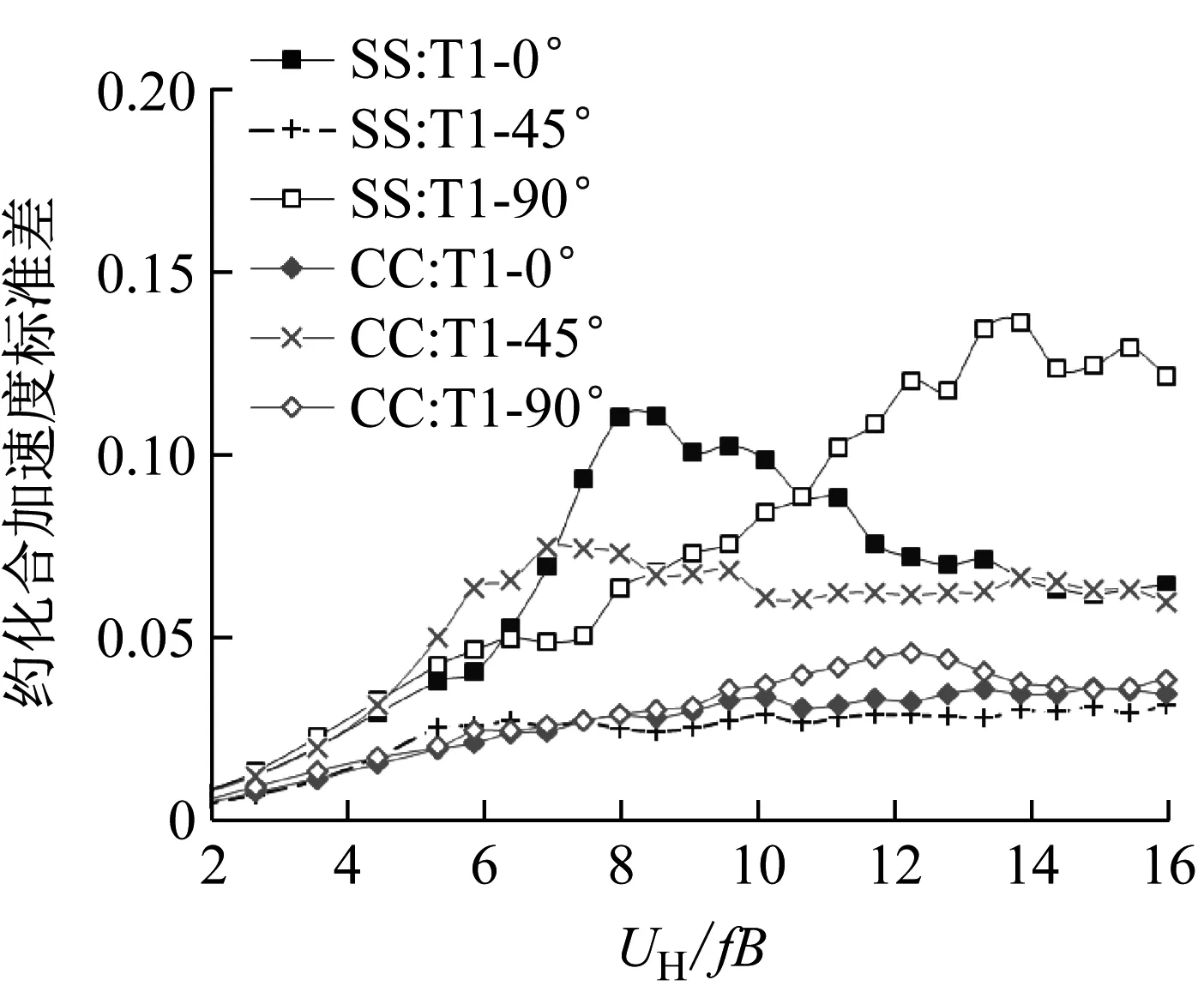
(a)T1塔楼
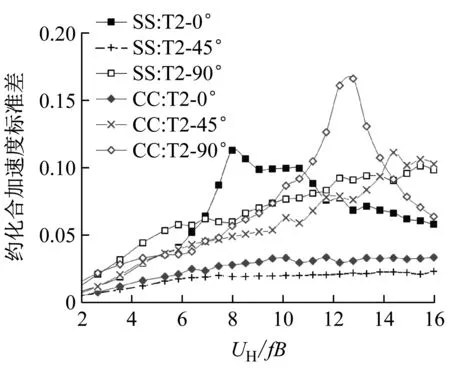
(b)T2塔楼图12 间距s/B=1.0时双塔风振加速度随约化风速的变化Fig.12 Variationofwind-inducedresultantaccelerationwithreducedwindspeedatspacings/B=1.0
从工程实际考虑,抗风设计需要控制的是所有风向下两栋塔楼中的最大风振加速度。根据以往的研究成果,面对面双塔出现最大风振加速度的最不利风向角比较固定,分别为0°和90°。而角对角双塔的最大风振加速度则在45°和90°附近有一定波动。因此需要在这两个风向角附近进行敏感性分析。同样以双塔间距1.0为例,图13给出角对角双塔在45°和90°风向角附近的风振加速度变化。
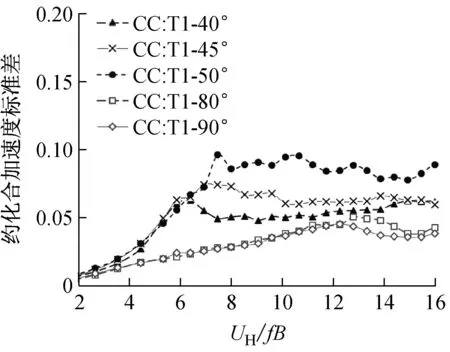
(a)T1塔楼
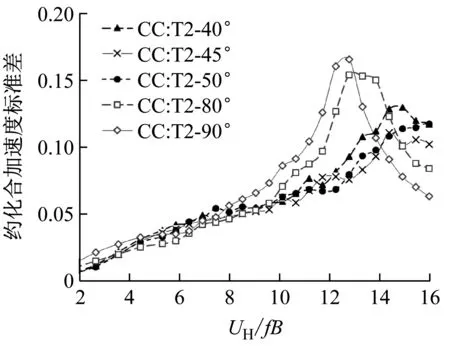
(b)T2塔楼图13 间距s/B=1.0时双塔风振加速度对风向角的敏感度Fig.13 Sensitivityofwind-inducedresultantaccelerationtowinddirectionatspacings/B=1.0
如图13所示,当风速较小时(UH/fB≤7),角对角布局的风振加速度对风向角的变化不敏感,但风速较大时,当风向角从45°转到50°时,上游塔的加速度会有明显增加,但下游塔的加速度会略有减少。当风向角从90°偏转后,虽然仍然出现较大的尾流激振,但出现峰值的约化风速会有所提高。
考虑所有风向角后,可以对不同间距下双子塔两种布局方式的最大风振加速度进行比较,见图14。作为比较,图中还给出对应独塔的风振加速度值。

(a)s/B=0.5
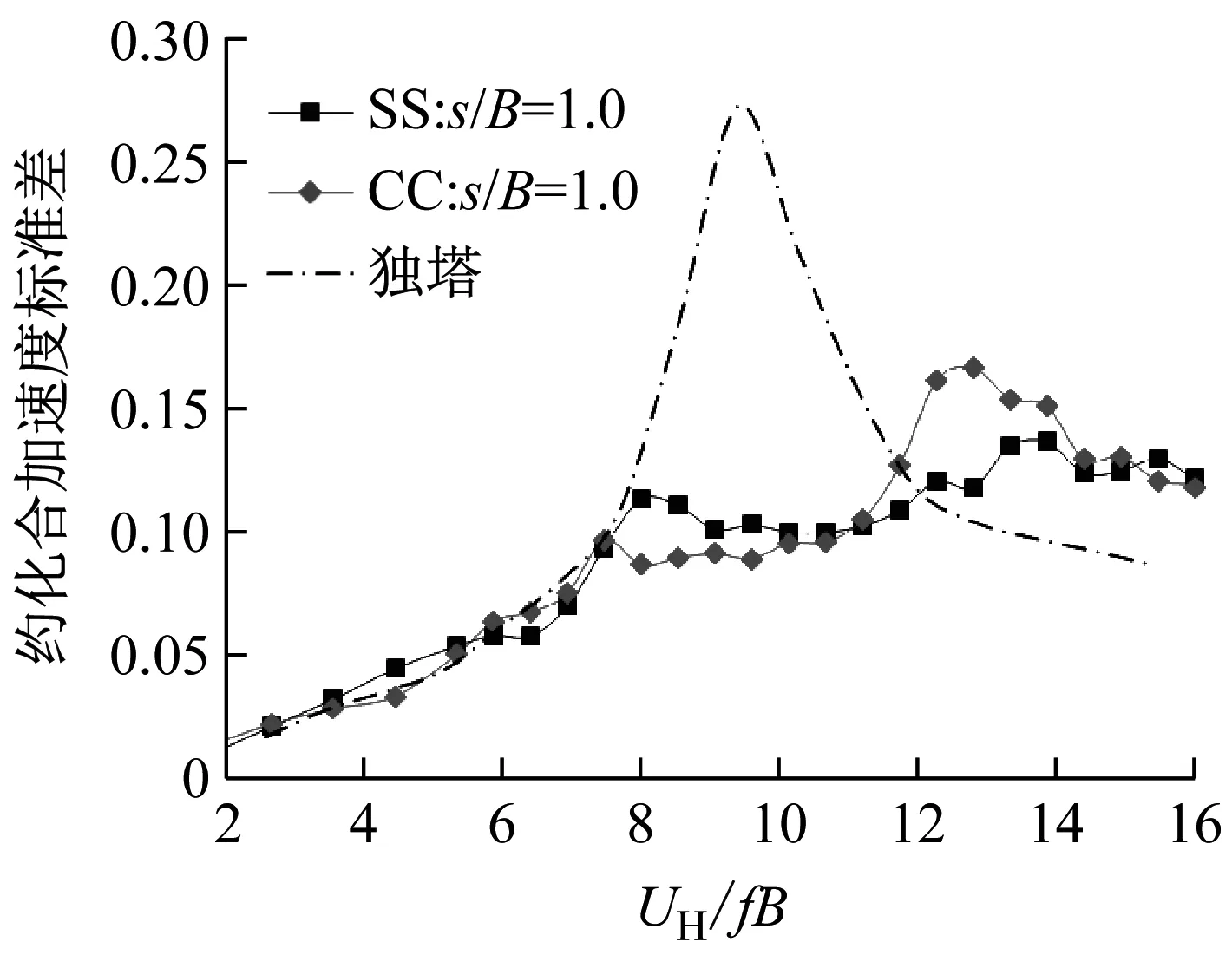
(b)s/B=1.0

(c)s/B=1.5

(d)s/B=2.0图14 不同间距下双塔最大风振加速度比较Fig.14 Comparisonofmaximumwind-inducedaccelerationatvariousspacing
由图14可见,在约化风速较小时(UH/fB≤7),面对面布局和角对角布局的风振加速度比较接近,没有明显的优劣之分。但当约化风速较大时,面对面布局和角对角布局下的加速度相对大小就会受到双塔相对间距的不同影响。
在小间距时(s/B≤0.5),双塔间的气动干扰比较强烈,使得两种布局下的涡激振动都受到有效抑制。但角对角布局时下游塔会出现强烈的尾流激振(对应约化风速12),但面对面布局时则没有发现类似振动。
在中等间距时(s/B=1.0),面对面布局下开始出现一定的涡激振动(对应约化风速8),而角对角布局时仍然存在尾流激振,但振幅已大大降低。
在大间距时(s/B为1.5到2.0之间),两种布局都出现涡激振动和尾流激振。但角对角布局时的涡激振动幅值明显低于面对面布局。当间距达到2.0时,面对面布局下横风向涡激振动幅值已与独塔情况相当,而且尾流激振幅值也大于角对角布局。
根据风洞试验结果可以看出双塔间的气动干扰作用主要与尾流效应和狭道效应有关。
当双塔串列布置时,气动干扰作用主要由尾流效应造成。表现为上游塔的尾流对下游塔周期性涡脱的干扰,以及下游塔对上游塔涡漩发育的干扰。因此在90°风向角下的面对面布局和45°风向角下的角对角布局下,涡激振动均得到非常显著的抑制。
当双塔并列布置时,气动干扰作用主要由狭道效应造成。气流通过双塔间的狭道,形成加速区,影响双塔内侧的气流分离。这一气动干扰作用对抑制涡激振动的效果不如尾流效应作用明显,而且随着双塔间距增大,狭道效应作用迅速弱化。因此面对面双塔的涡激响应往往由0°风向角控制。与此相比,角对角双塔的最不利风向角在45°左右,能始终得益于上下游形成的气动干扰作用。
综合以上分析,从风致振动方面考虑可以认为当双塔间距很小时(s/B为0.5左右或更小),面对面布局比较有利;而当双塔间距较大时(s/B为1.5~2.0),角对角布局比较有利。在中等间距时(s/B在1.0左右),则需要结合设计风速来决定两种布局的优劣。如果设计风速对应的约化风速达到12,则面对面布局较优,反之则以角对角布局为优。考虑到在结构设计中,风振加速度主要用于验算居住舒适性等性能化指标,对应十年回归期以下较低的参考风速,所以在绝大多数情况下,中等间距双子塔仍以角对角布局为优。
3.2 基底总风荷载的比较
与风振加速度不同,在比较两种布局下的设计风荷载时还必须考虑风荷载平均分量(即风荷载的定常分量)的影响。
以所有风向下两栋塔楼中的最大倾覆力矩为比较指标,图15给出不同间距下的结果。

(a)s/B=0.5
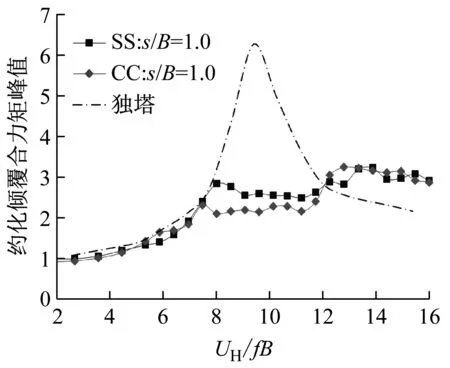
(b)s/B=1.0

(c) s/B=1.5

(d) s/B=2.0图15 不同间距下双塔最大倾覆力矩比较Fig.15 Comparison of maximum overturning moment at various spacing
由图15可见,不同间距下两种布局的风荷载随风速的变化规律与加速度情况基本相似,差别仅出现在较低约化风速范围内。这是因为在较低约化风速范围内,最不利风荷载工况由顺风向响应控制,其中定常分量占比较大。而在较高约化风速时,最不利风荷载工况由横风向响应控制,相应的变化规律与横风向风振加速度基本一致。
值得指出,由于双塔间的气动干扰作用(包括尾流效应与狭道效应),双子塔涡激振动的振幅一般不大于相应独塔的情况。只有当双塔间距较大时(例如相对间距s/B=2.0),双子塔涡激振动的振幅才会接近独塔情况,见图15(d)。
以间距s/B=1.0为例,图16分别给出面对面布局在约化风速为8和角对角布局在约化风速为12时的基底倾覆力矩的时程。可以看出面对面布局不利工况反映了0°风向角时横风向振动荷载为主的荷载情况,其中顺风向荷载以定常分量为主。而角对角布局不利工况反映了90°风向角时下游塔横风向荷载为主的荷载情况,其中下游塔的顺风向荷载几乎可以忽略。上游塔的顺风向荷载虽然较大,但横风向荷载很小。这反映了典型的尾流激振荷载情况。

(a)面对面布局双塔s/B=1.0;风向角=0°;UH/fB=8
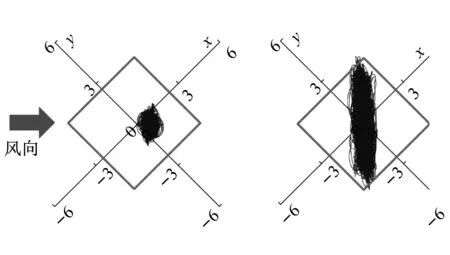
(b)角对角布局双塔s/B=1.0;风向角=90°;UH/fB=12图16 两种布局下典型的约化倾覆力矩时程轨迹Fig.16 TypicaltrajectoriesofreducedoverturningmomentsfortwoexaminedconFigurations
4 结 论
采用风洞试验方法对面对面与角对角两种布局下的双子塔的气动特性与抗风性能进行了对比研究,主要得到如下结论:
(1) 由于双子塔面对面布局和角对角布局所产生的气动干扰有所不同,因此相应的气动力频谱特性之间存在明显差异。
(2) 在约化风速较小时(UH/fB小于7左右),面对面布局和角对角布局的风振加速度和整体风荷载比较接近,没有明显的优劣之分。但当约化风速较大时,面对面布局和角对角布局下的风致响应将会受到双塔相对间距的不同影响,造成抗风性能方面的差异。
(3) 在小间距时(相对间距s/B为0.5左右或更小),双塔间的气动干扰比较强烈,使得两种布局下的涡激振动都受到有效抑制。但角对角布局时下游塔会出现强烈的尾流激振(对应约化风速12左右),但面对面布局时则没有发现类似振动。在这种情况下可以认为面对面布局对抗风设计比较有利。
(4) 在中等间距时(相对间距s/B在1.0左右),面对面布局下开始出现一定的涡激振动(对应约化风速8左右),而角对角布局的涡激振动幅值则很小。虽然当风沿双塔串联方向时,角对角布局的风振加速度略高于面对面布局,但两者的风荷载相差不多。因此可以认为角对角布局对抗风设计比较有利。
(5) 在大间距时(相对间距s/B为1.5~2.0),两种布局时都出现涡激振动和尾流激振。但角对角布局时的风振加速度和整体风荷载幅值均明显低于相应的面对面布局。当间距达到2.0时,面对面布局下横向涡激振动幅值已与独塔情况相当,但角对角布局时双塔间的气动干扰仍然发挥着有利的作用。角对角布局在涡激临界风速附近的结构风荷载只有面对面布局的60%左右。

