高速铁路车轮扁疤智能识别算法的曲线适应性
刘旭麒, 和振兴, 杨丽蓉
(兰州交通大学 机电工程学院, 兰州 730070)
存在扁疤故障的列车在运行过程中会产生周期性的冲击,影响乘坐舒适性甚至危害行车安全。对车轮扁疤准确识别、跟踪其发展、实现车轮扁疤维修从计划修到状态修转变,是智能故障检测的发展目标。
目前我国动车组大都采用计划修,定期探伤检测来识别和处理车轮病害。为了保证运行安全性往往要制定较短的维修周期,因此会增加维修成本和不必要的停机时间,如果能够在正常运行过程中通过智能监测跟踪车轮扁疤的变化,将会大大降低维修成本。因此,在运行过程中实现智能监测以及采用一种线性化的指标对车轮扁疤进行评估是尤为重要的。
由于高速铁路运行过程中存在大量的曲线线路,智能识别算法在曲线地段的适应性是实现对车轮扁疤全线不间断识别跟踪的前提。高速铁路曲线地段轮轨之间的动力相互作用复杂,曲线线路与直线线路轮轨力差异显著,研究曲线线路条件下车轮扁疤智能识别算法的识别效果是尤为重要的。
Marijonas等[1]采用了一种确定车轮扁疤与轨道相互作用下车轮垂直冲击力的简化方法,得出扁疤冲击力大小取决于扁疤尺寸、车轮直径和车速。凌亮等[2]分析了车轮擦伤对轮轨法向作用力及轮对垂向振动加速度的影响。敬霖等[3]从多方面分析了车轮扁疤损伤对列车动力学的影响。上述研究重点关注了直线线路车轮扁疤损伤对车辆和轨道系统的动力学影响以及相关特性,但很少有在曲线线路下研究车轮扁疤的动力学响应。
针对车轮扁疤故障的识别,Liang等[4]利用轴箱加速度和信号处理算法检测车轮扁疤,此方法虽然能实时检测车轮扁疤,但所需传感器数目太多,数据处理量太大;Chen等[5]提出了一种用于车轮扁疤检测的两级自适应线性调频模式分解(ACMD)方法。Bosso等[6]通过轴箱振动加速度来识别车轮扁疤。Li等[7]提出了一种自适应多尺度形态滤波(AMMF)算法来检测车轮扁疤。李奕璠等[8]利用改进的经验模态分解和Hilbert-Huang变换,对轴箱垂向振动特征进行扁疤识别,但此方法只能判断车轮是否产生故障,不能对扁疤长度进行识别。田丽丽等[9]利用剥离和擦伤的定位方法对货车车轮擦伤进行识别,研究得出擦伤定位准确率达到97.8%。史红梅等[10]对钢轨振动响应进行高阶谱分析,研究得出高阶谱分析能够定量判断扁疤深度,且识别能力不受轨道不平顺及列车速度的影响。宋颖等[11]利用连续小波变换系数模极大值来处理扁疤轴箱振动加速度信号。以上研究重点关注了车轮扁疤的识别,但其考虑的线路条件均为直线线路。由于高速铁路存在大量的曲线地段,所以研究车轮扁疤智能识别算法在曲线地段的适应性是非常必要的。
本文提出了一种基于变分模态分解的高速铁路车轮扁疤智能识别算法,通过建立车辆—轨道耦合动力学模型,对仿真计算得到的轮轨力采用变分模态分解并进行信号重构和包络谱分析。该算法在直线地段可以准确识别不同速度对应的扁疤冲击频率及其倍频,包络谱前4阶倍频对应幅值的均值与扁疤长度之间存在线性关系,可以对扁疤长度进行准确识别。本文重点研究曲线地段使用该算法识别车轮扁疤的适应性。
1 车辆-轨道耦合动力学模型
1.1 车辆系统动力学模型
采用车辆-轨道耦合动力学理论,建立了CRH380B型车的动力学模型,由车体、转向架、轴箱、轮对等部件组成,其中弹性元件均采用力元表示。模型中考虑了悬挂系统以及轮轨接触的非线性,车辆系统振动响应微分方程为
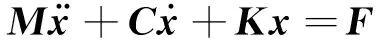
(1)

轨道模型采用柔性轨道,轨道随机不平顺选用德国低干扰谱,曲线线路参考《高速铁路设计规范》[12],具体参数如表1所示。

表1 曲线线路参数Tab.1 Curve line parameters
1.2 高速车轮扁疤冲击机理及模型
在运行过程中由于制动或空转打滑,车轮踏面容易出现局部擦伤和剥离,造成车轮扁疤,图2为列车高速运行时扁疤车轮的运动示意图。
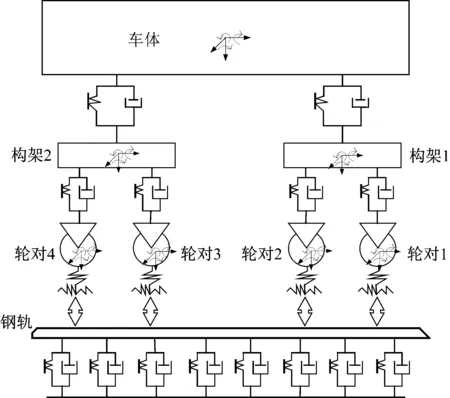
图1 车辆-轨道耦合动力学模型Fig.1 Vehicle-track coupling dynamics model

图2 扁疤车轮运动示意图Fig.2 Motion diagram of flat wheel
由图2可以看出当列车高速运行时,车轮滚至A点后在惯性的作用下使车轮悬空,同时向下跌落,最终在B点接触轨面并产生冲击。
文献[13]对高速车轮扁疤冲击机理做了详细的论述,高速时的车轮冲击速度为
(2)
式中:L为扁疤长度;R为车轮半径;v为车速;γ为车轮旋转惯量转换为往复惯量的系数;μ为车轮向下跌落的加速度,其满足
μ=(M1+M2)/(M2g)
(3)
式中:M1、M2分别为车辆一系簧上、簧下质量;g为重力加速度。
车轮扁疤模型如图3所示。

图3 车轮扁疤模型Fig.3 Wheel flat model
2 VMD分解及包络谱理论
2.1 VMD分解基本理论
变分模态分解(variational modal decomposition, VMD)是基于傅里叶分解的一种新型对非平稳信号的分解方法,其利用变分分解框架能够很好地弥补经验模态分解(empirical mode decomposition, EMD)模态混淆及端点效应等不足,可以人为的指定分解个数且具有较高的分解精度。
VMD是将一个原始信号f(t)分解成k个模态分量,每个模态分量以中心频率ωk进行分解,其约束条件是所有模态函数和等于原始信号f(t)[14]
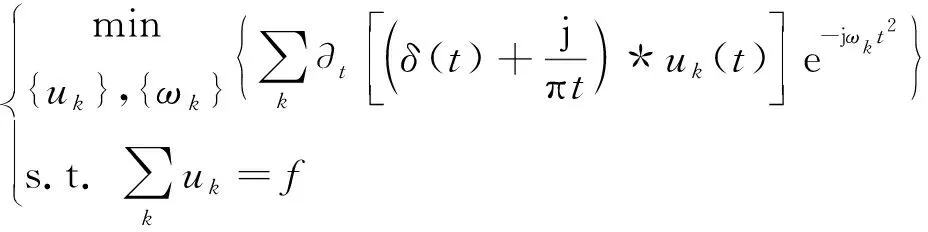
(4)
式中:{uk}={u1,…,uk}为分解后的K个模态分量;{ωk}={ω1,…ωk}为分解后对应每个模态分量的中心频率。
为了求解式(4),通过引入拉格朗日乘子λ(t)和二次惩罚因子α,将约束变分问题变为非约束变分问题,延伸后的拉格朗日表达式如下

(5)
通过采用乘法算子交替方向法来解决式(5)的非约束性问题,从两个方向交替更新uk和ωk完成VMD分解
(6)
(7)
VMD分解具体过程如下:
(2) 重复n←n+1;
(3) 分解个数从 1~k对所有的ω≥0,更新uk,ωk,直到满足迭代终止条件
(8)
式中,ε为判别精度,ε>0。
2.2 包络谱基本理论
包络谱对冲击故障比较敏感,同时剔除了不必要的频率干扰,更能凸显故障特征频率。包络谱分析的步骤为:
(1) 对信号进行Hilbert变换,即:
(9)
(2) 构造信号z(t)
z(t)=x(t)+jh[x(t)]
(10)
(3) 求信号的包络:
(11)
(4) 对包络信号做谱分析得到包络谱
2.3 扁疤识别流程
本文以VMD分解作为基础,以包络谱分析作为核心进行车轮扁疤故障识别,首先通过上述多体动力学模型计算得到轮轨力信号;然后通过VMD分解得到各IMF分量;再筛选特定的IMF分量并将其进行重构;最后通过包络谱识别扁疤冲击倍频,其流程如图4所示。
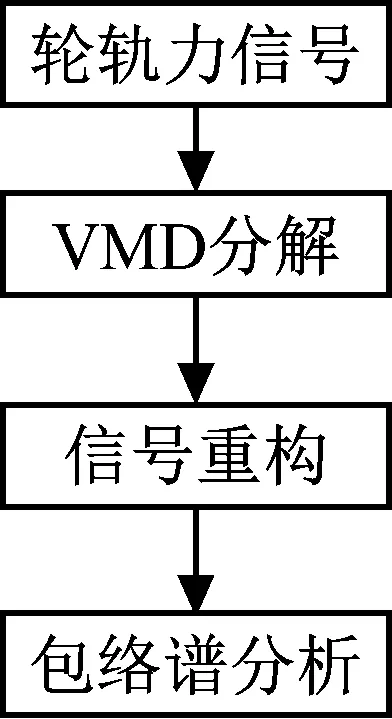
图4 扁疤识别流程图Fig.4 Flat recognition flow chart
3 信号的VMD分解与重构
3.1 轮轨力的时域信号
为了校验模型的准确性,对比了实测轮轨力信号和仿真计算得到的轮轨力信号。图5为国内某线路350 km/h速度下实测外轨曲线轮轨力,图6为350 km/h速度下仿真计算得到的外轨曲线轮轨力,可以看出仿真计算得到的轮轨力与实测轮轨力变化趋势基本一致。
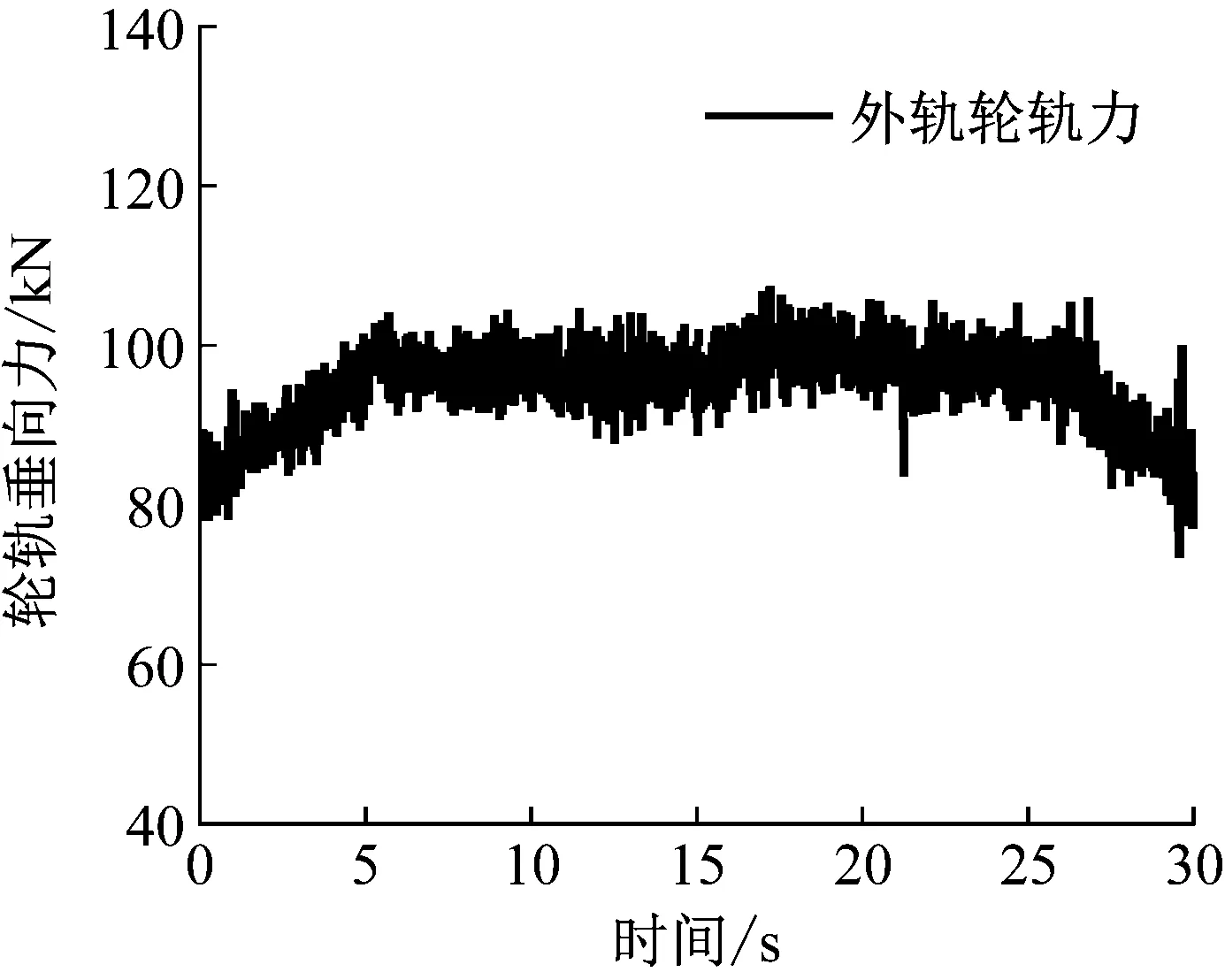
图5 实测外轨曲线轮轨力Fig.5 Measured outside rail curve wheel-rail force
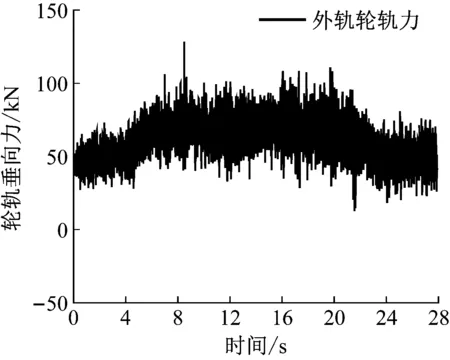
图6 仿真外轨曲线轮轨力Fig.6 Simulation of outside rail curve wheel-rail force
图7和图8为350 km/h速度下通过理论计算得到的外轨侧轮轨力信号,为了方便观察只截取了部分信号。图7为无故障情况下对应的轮轨力,图8为存在10 mm长度车轮扁疤时对应的轮轨力。

图7 无故障工况下的轮轨力Fig.7 Wheel-rail force in fault-free condition
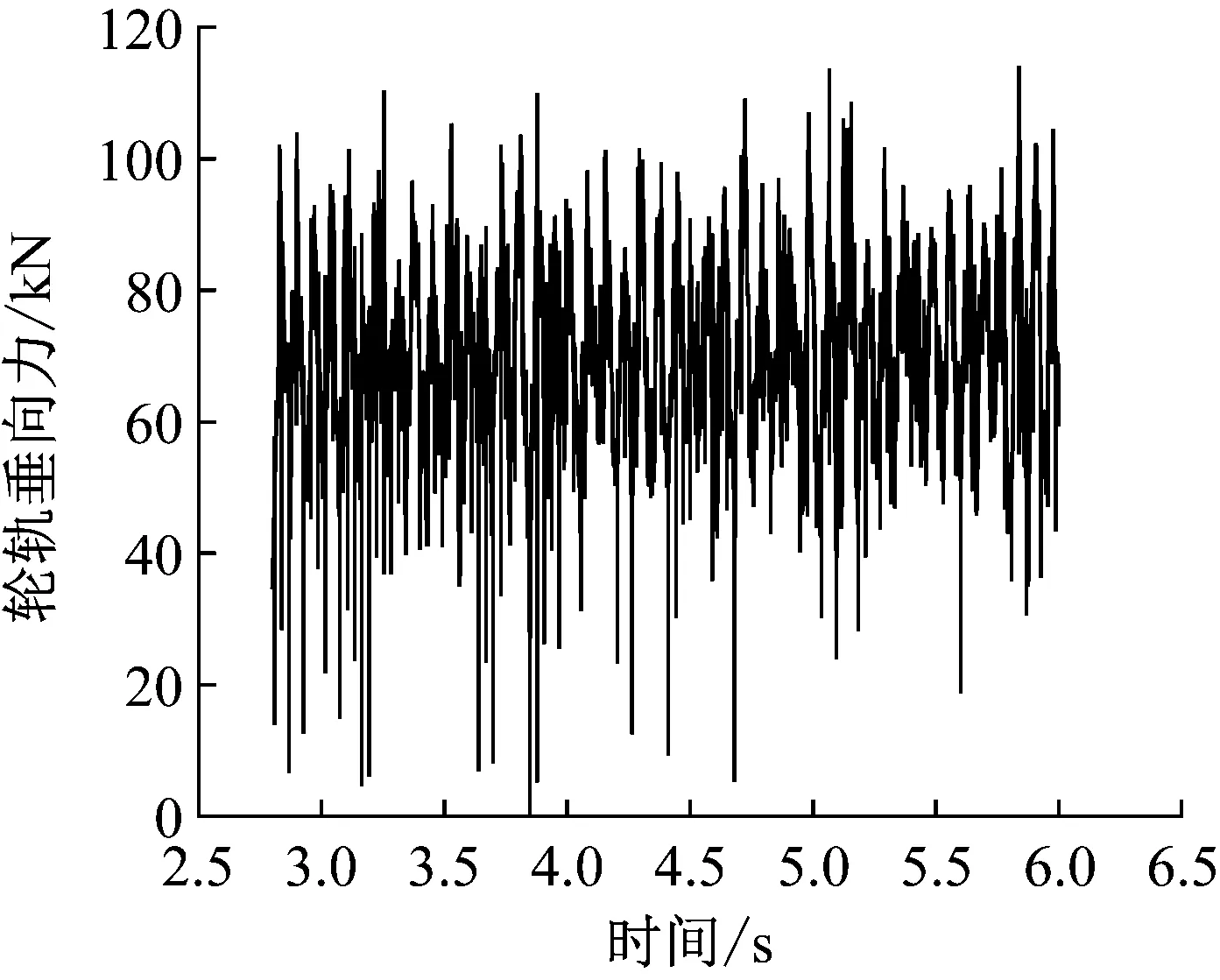
图8 10 mm扁疤对应的轮轨力Fig.8 Wheel-rail force under 10 mm wheel flat
从图7和图8中可以看出当扁疤长度较低时,在时域中由于存在随机信号的干扰难以观测出扁疤冲击,同时无法根据幅值大小准确衡量扁疤长度。因此,在时域信号中难以对车轮扁疤长度进行识别。
3.2 轮轨力的分解与重构
考虑曲线线路特性,本文分别提取缓和曲线和圆曲线对应300 m长度的轮轨力信号进行分析。
对缓和曲线和圆曲线线路下的轮轨力分别进行VMD分解,首先需要确定分解层数K和平衡约束参数α。当K取值过小时VMD分解会出现模态混叠,反之信号会出现过分解。本文根据EMD分解结果确定VMD分解阶数,以EMD分解得到的阶数作为VMD分解阶数。因此设置分解层数K=10,平衡约束参数α取默认值2 000,图9为350 km/h速度下,外轨侧存在10 mm长度扁疤轮轨力的变分模态分解结果,图9(a)为缓和曲线线路下的分解结果,图9(b)为圆曲线线路下的分解结果。
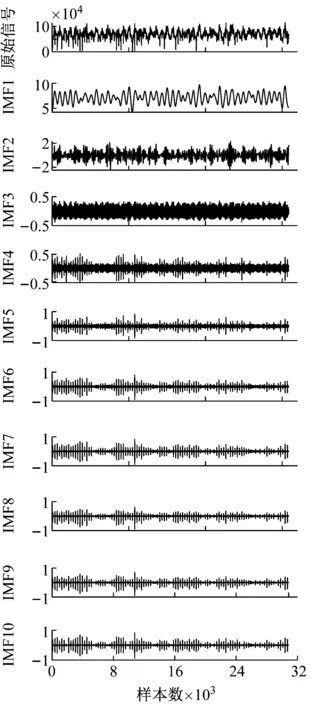
(a) 缓和曲线上的VMD分解
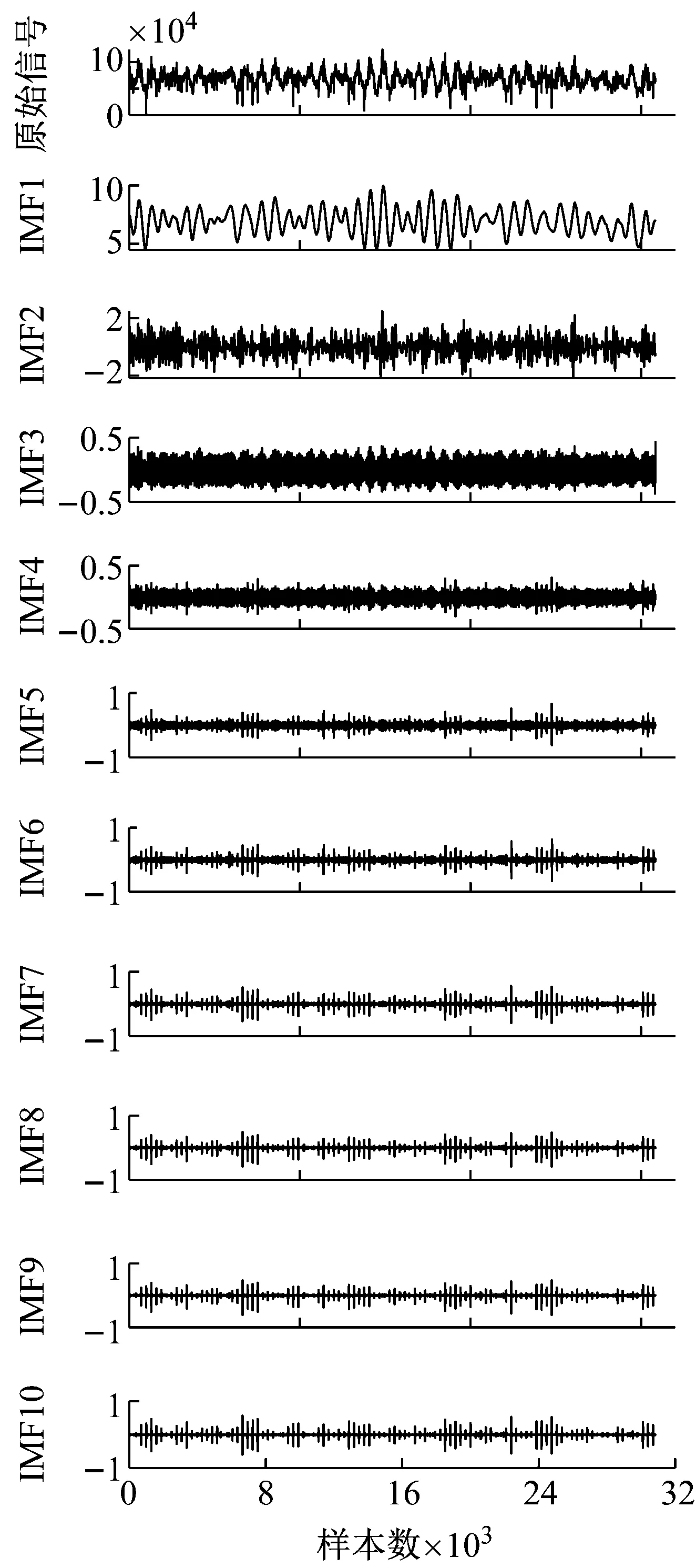
(b) 圆曲线上的VMD分解图9 曲线外轨侧轮轨力的VMD分解Fig.9 VMD decomposition of outside rail curve wheel-rail force
图9表明,无论在圆曲线上还是在缓和曲线上,各IMF分量中IMF1 ~ IMF3信号的周期性冲击特征不明显,对扁疤冲击的反映能力低。IMF4 ~ IMF10中周期性的冲击特征明显,反映的就是扁疤冲击。为了更准确地提取扁疤冲击信号,将图9中的IMF4 ~ IMF10进行信号重构,重构信号如图10所示。

图10 不同扁疤长度对应的轮轨力重构信号Fig.10 Wheel-rail force reconstruction signals under different wheel flat lengths
由于篇幅原因,本文只展示了外轨侧缓和曲线的轮轨力重构信号,从图10中可以看出重构信号更直观地反映了扁疤冲击,剔除了与扁疤冲击无关的成分,更适合进行故障诊断。随着扁疤长度的增大,重构信号的幅值也随之增大。
4 扁疤冲击频率特性及识别
为了能够准确识别扁疤冲击频率特性,本文采用包络谱分别对不同轨侧、不同曲线线路的重构信号进行分析。
4.1 350 km/h速度下曲线线路的包络谱
4.1.1 外轨缓和曲线地段的包络谱
对重构信号进行包络谱分析,结果如图11所示。图11(a)为无故障工况下重构信号的包络谱,图11(b)~ 图11(f)为不同扁疤长度下重构信号的包络谱,分析频率范围为0~ 600 Hz。
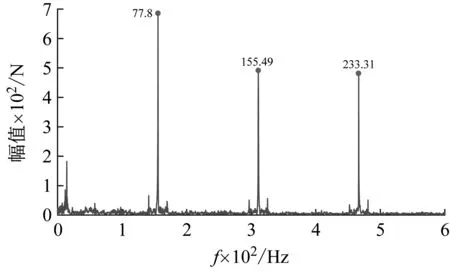
(a) 无故障工况下的包络谱
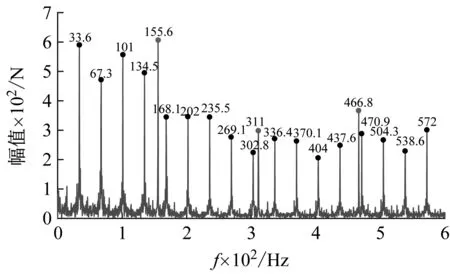
(b) 10 mm扁疤工况下的包络谱
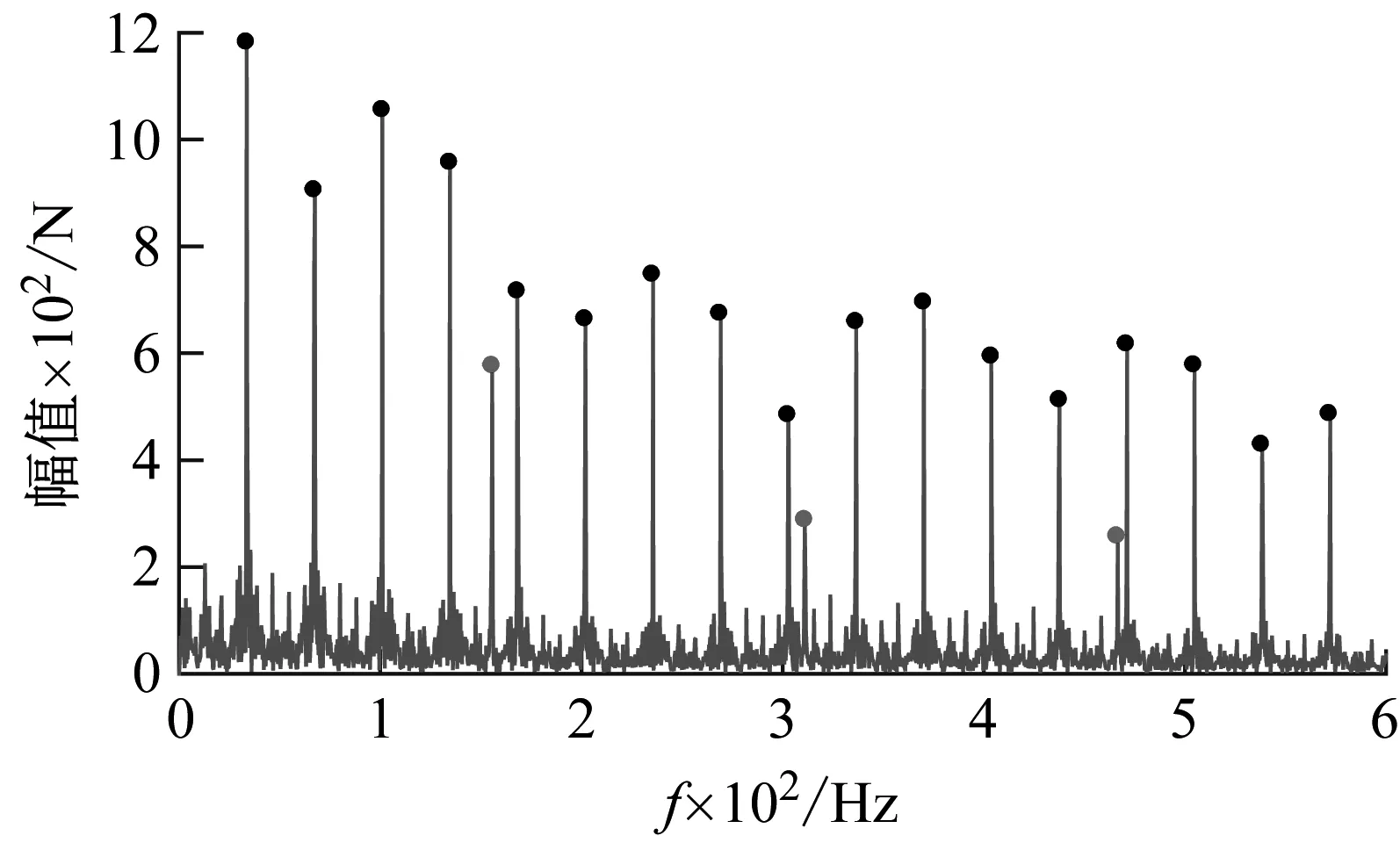
(c) 20 mm扁疤工况下的包络谱
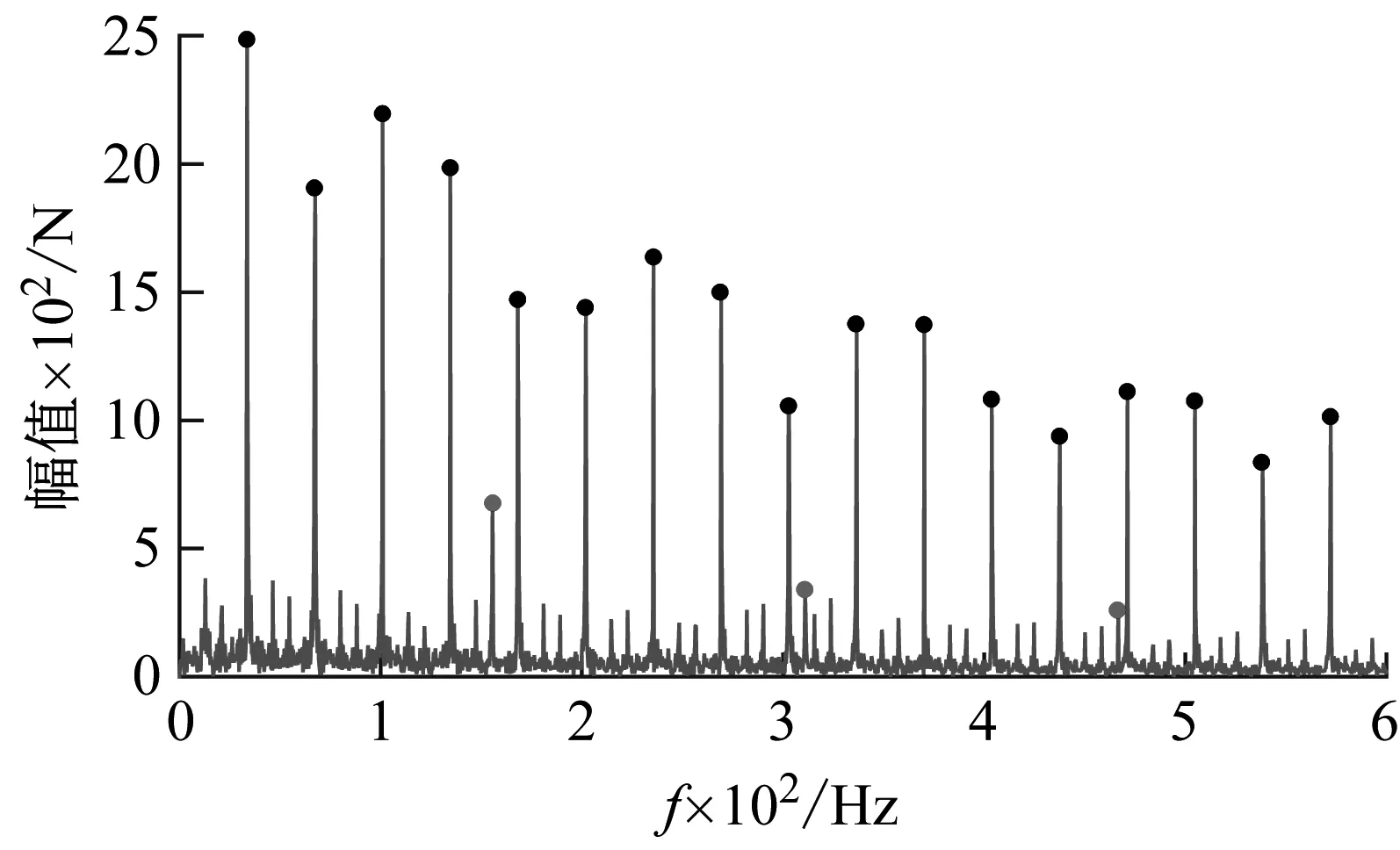
(d) 30 mm扁疤工况下的包络谱
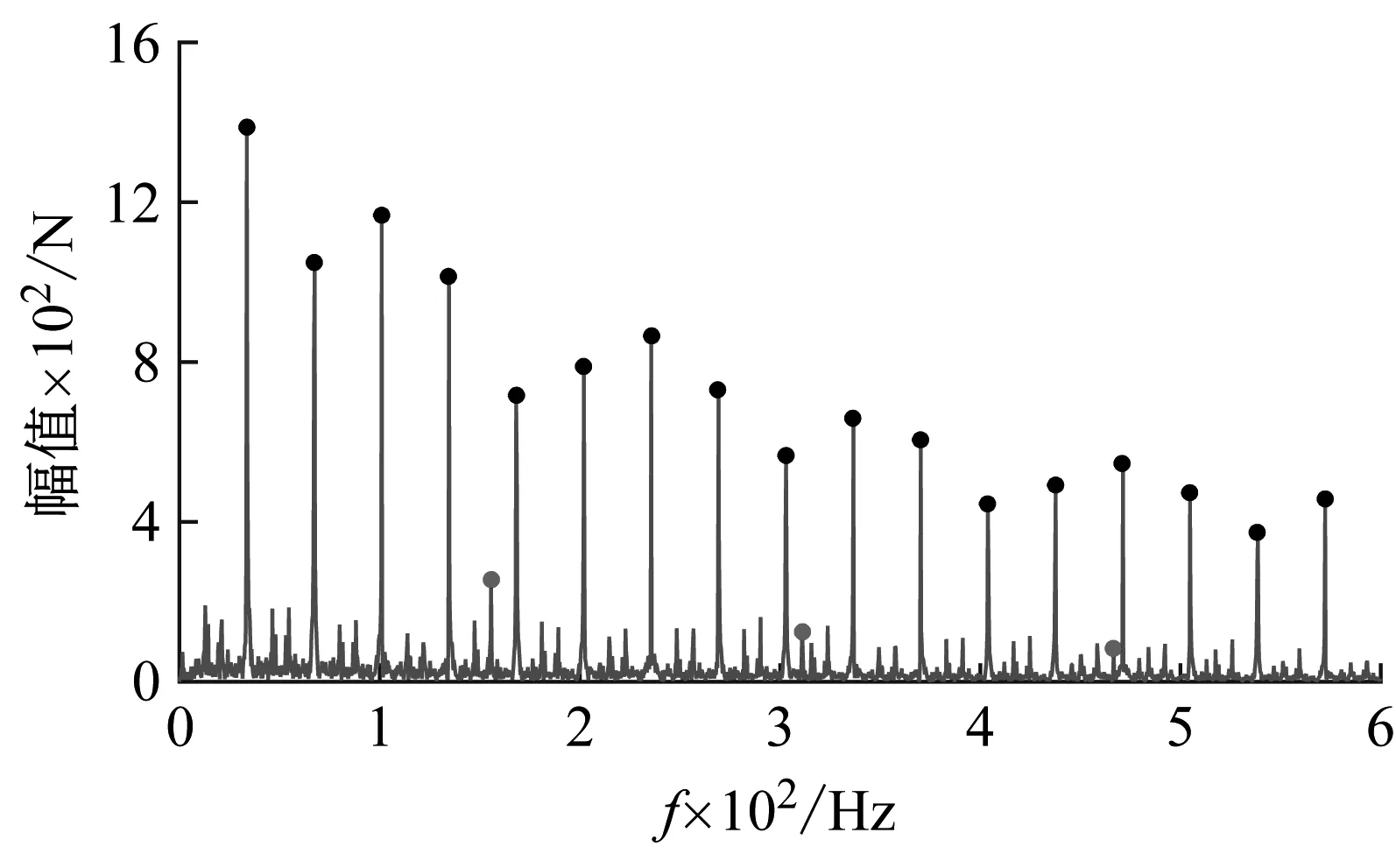
(e) 40 mm扁疤工况下的包络谱

(f) 50 mm扁疤工况下的包络谱图11 外轨缓和曲线包络谱Fig.11 Envelope spectrum of outside rail on transition curve
图11中黑色圆点标记代表扁疤冲击频率及其倍频,其与列车运行速度的关系为
(12)
式中:v为列车运行速度;R为轮径。
根据式(12),对应于350 km/h列车速度扁疤冲击频率为33.6 Hz及其倍频,这与图11(b)~ 图11(f)中对应的扁疤冲击频率一致。
图11中圆点标记是与扁疤冲击无关的干扰信号,且具有倍频特征。根据扣件支撑间距与行车速度之间的关系
(13)
式中:v为列车运行速度;L为扣件支撑间距。
可以得出,扣件支撑频率为155.6 Hz及其倍频,与图11中圆点标记代表的干扰信号的频率一致。
图11(a)表明,当不存在车轮扁疤时,轮轨力重构信号的包络谱中主要存在的频率成分为扣件支撑频率及其倍频。
由图11(b)可以看出,当车轮踏面存在10 mm长度的车轮扁疤时,轮轨力重构信号的包络谱中同时出现车轮扁疤冲击倍频和扣件支撑倍频,扣件支撑倍频对应的幅值略大于扁疤冲击倍频对应的幅值。如果将扣件支撑频率从包络谱中剔除,就可以准确识别出扁疤冲击频率。
从图11(c)~ 图11(f)可以看出,当扁疤长度在20 mm以上时,扁疤冲击倍频为轮轨力重构信号包络谱中的主要成分,扣件支撑倍频对应的幅值远小于扁疤冲击倍频对应的幅值,不对识别产生影响,可以直接进行识别。
4.1.2 外轨圆曲线地段的包络谱
图12(a)为无故障工况下重构信号的包络谱,图12(b)~ 图12(f)为不同扁疤长度下重构信号的包络谱。
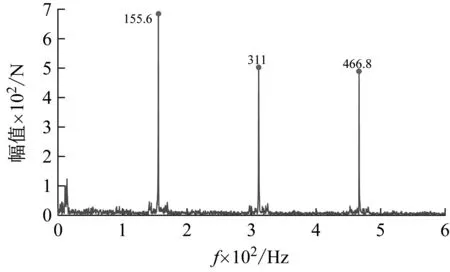
(a) 无故障工况下的包络谱

(b) 10 mm扁疤工况下的包络谱
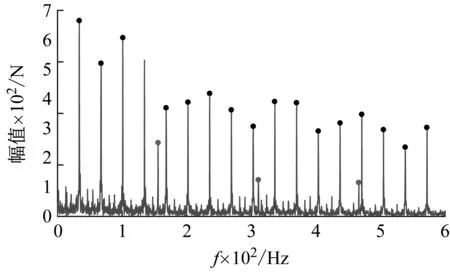
(c) 20 mm扁疤工况下的包络谱

(d) 30 mm扁疤工况下的包络谱

(e) 40 mm扁疤工况下的包络谱

(f) 50 mm扁疤工况下的包络谱图12 外轨圆曲线包络谱Fig.12 Envelope spectrum of outside rail on circular curve
从图12可以看出除了在幅值大小上有所区别外,圆曲线各扁疤长度的包络谱与缓和曲线包络谱变化规律及相关特征基本一致。
4.1.3 内轨曲线包络谱
内轨缓和曲线和圆曲线车轮扁疤对应的包络谱分别与图11、图12的规律一致,由于篇幅原因本文不再详细给出。
4.2 250 km/h速度下的曲线线路的包络谱
为了验证该算法在不同速度下的适用性,计算了列车以250 km/h速度通过上述曲线时不同车轮扁疤对应的包络谱,其规律与上述350 km/h速度下的基本一致。由于篇幅原因给出部分外轨缓和曲线的包络谱,如图13所示。
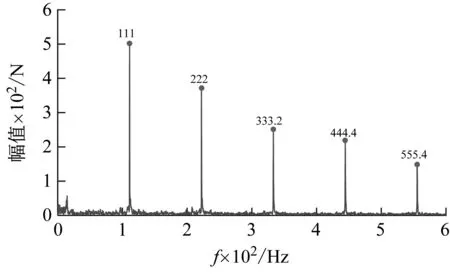
(a) 无故障工况下的包络谱
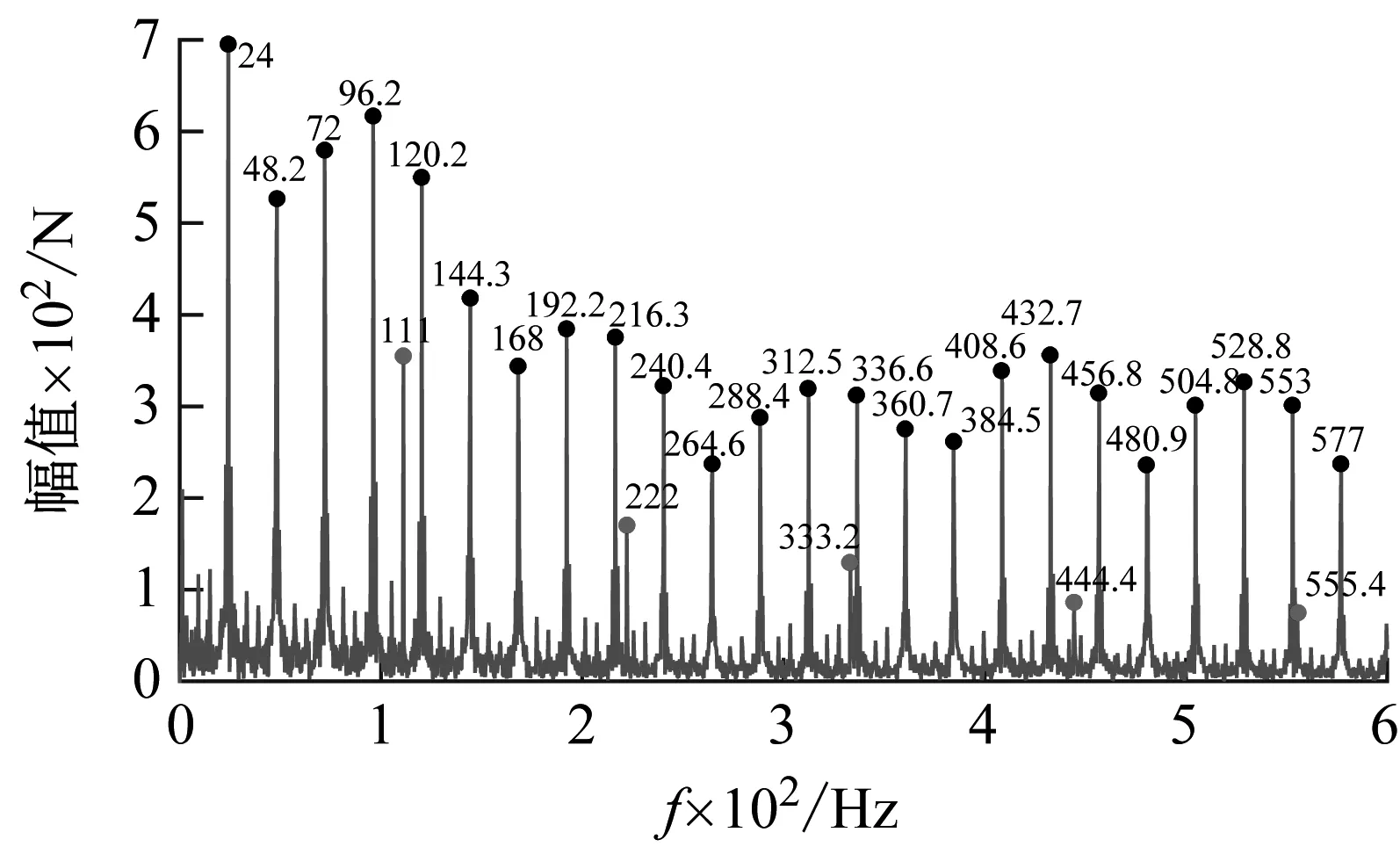
(b) 10 mm扁疤工况下的包络谱
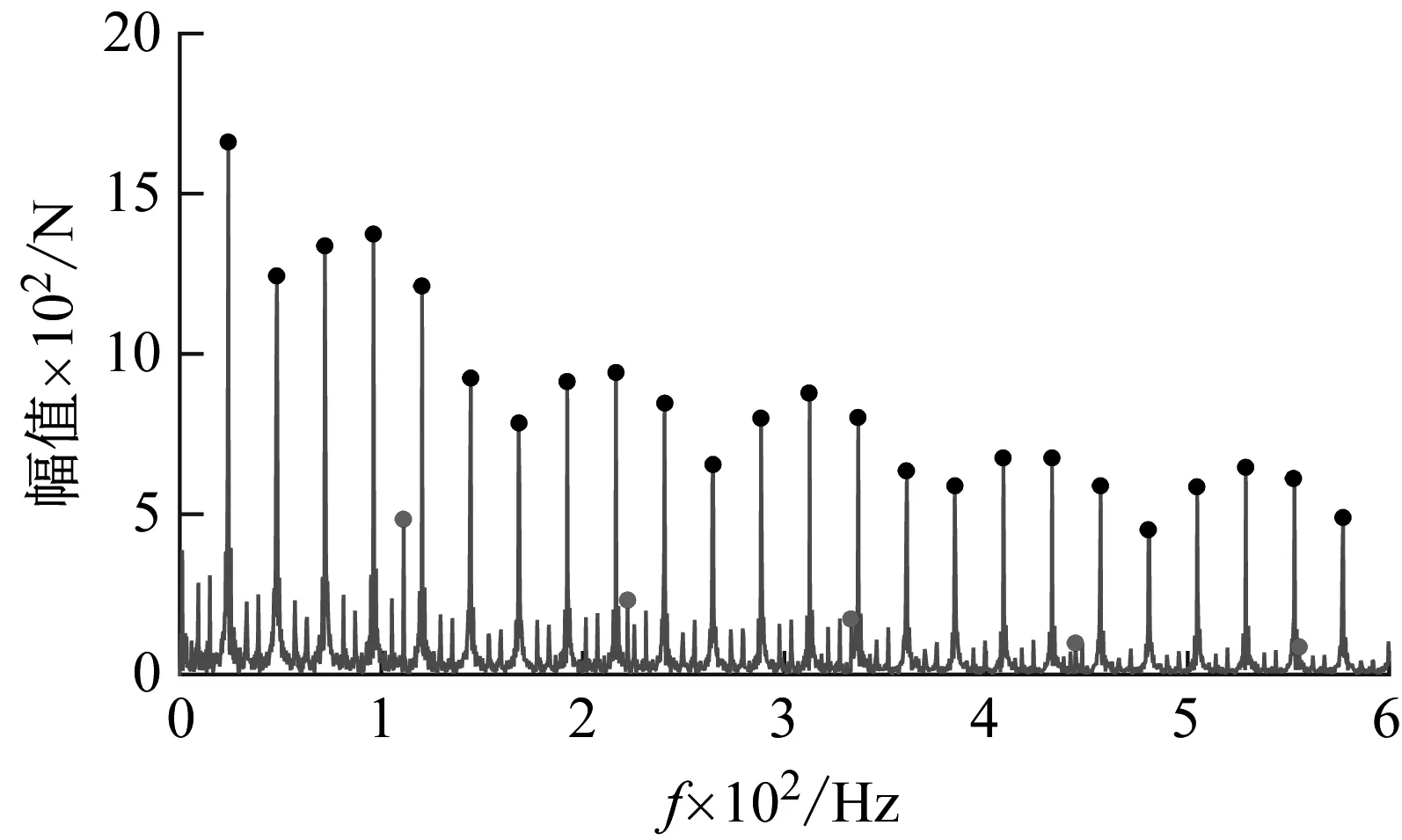
(c) 20 mm扁疤工况下的包络谱图13 外轨缓和曲线包络谱Fig.13 Envelope spectrum of outside rail on transition curve
图13为部分扁疤长度下的外轨缓和曲线包络谱。经计算250 km/h速度下扁疤冲击频率和扣件支撑频率分别为24 Hz和111 Hz,可以看出重构信号包络谱中各扁疤冲击频率对应幅值的变化规律与上文基本一致,倍频关系明显。
综上所述,在曲线线路的不同地段上,不同速度、不同轨侧各扁疤长度对应重构信号的包络谱具有一致规律,倍频特征明显。因此,在曲线线路上,该算法可以通过冲击频率及其对应的峰值判断车轮是否存在扁疤。
4.3 扁疤冲击频率的识别误差
根据包络谱识别出的扁疤冲击频率与理论冲击频率的误差如表2所示,扣件支撑频率与理论冲击频率的误差如表3所示,由于篇幅原因只列出了幅值较大的前4阶倍频。

表2 扁疤冲击频率误差Tab.2 Impact frequency error of wheel flat

表3 扣件支撑频率误差Tab.3 Impact frequency error of fastener support
从表2、表3可以看出包络谱识别出的扁疤冲击频率与理论计算得到的冲击频率误差小,前4阶倍频误差最大仅为0.4 %;扣件支撑频率与理论冲击频率的误差最大仅为0.09 %。因此该算法可以准确判定扁疤冲击倍频和扣件支撑倍频,其对车轮扁疤的识别精确度高。
5 扁疤长度的识别
从上文可以看出,250 km/h、300 km/h和350 km/h速度下包络谱幅值较大的成分主要集中于前4阶倍频。因此本文选取前4阶倍频对应的幅值并取其均值,其与扁疤长度之间的关系如图14到图17所示,其中图14为不同速度下直线线路对应的前4阶包络谱均值;图15~图17为直线与曲线线路不同地段对应前4阶包络谱均值的对比。
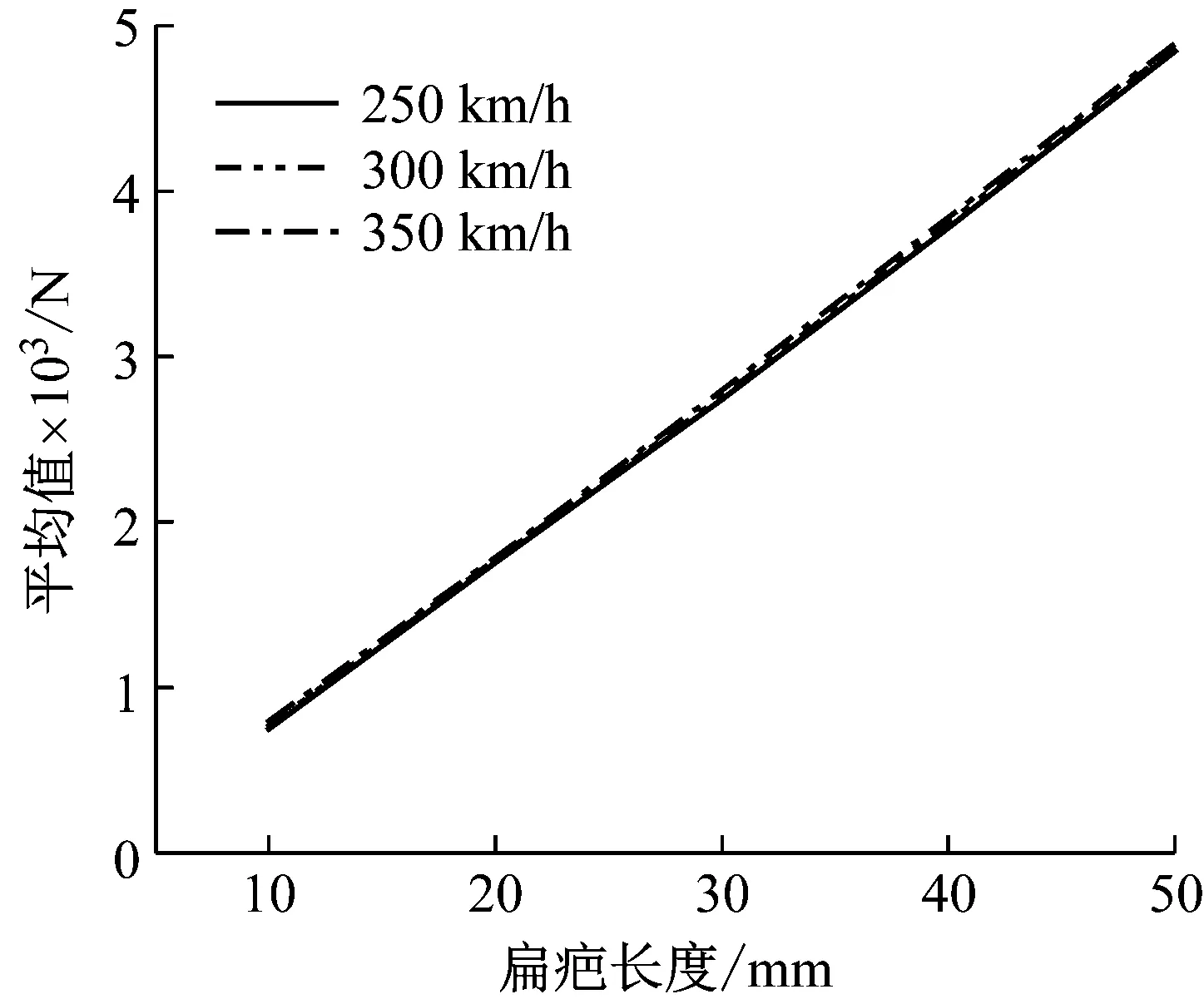
图14 直线线路前4阶包络谱均值Fig.14 The mean value of the first 4 order envelope spectrum on straight line

图15 250 km/h速度下包络谱均值的对比Fig.15 Comparison of envelope spectrum mean values at 250 km/h
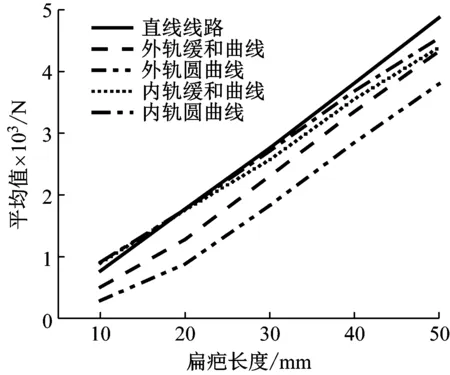
图16 300 km/h速度下包络谱均值的对比Fig.16 Comparison of envelope spectrum mean values at 300 km/h
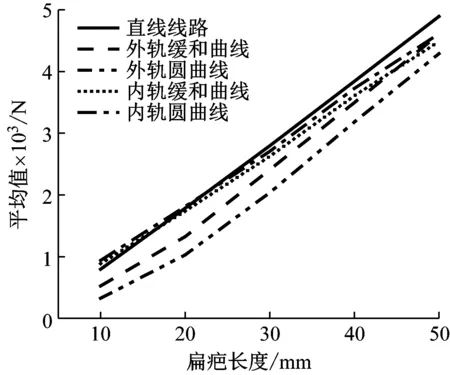
图17 350 km/h速度下包络谱均值的对比Fig.17 Comparison of envelope spectrum mean values at 350 km/h
从图14可以看出在直线线路中,不同速度对应的前4阶包络谱均值与扁疤长度之间呈线性关系,可以通过包络谱均值直接识别扁疤的长度。列车运行速度对扁疤长度识别准确性的影响可以忽略,说明本文提出的基于变分模态分解的智能识别方法在直线线路可以对车轮扁疤的长度进行准确识别。因此以直线线路包络谱均值与扁疤长度之间的线性关系为基准,研究该方法在曲线地段识别车轮扁疤长度的可行性。
图15~图17是列车分别以250 km/h、300 km/h和350 km/h速度通过上文所述半径为7 000 m的曲线时,曲线线路不同地段前4阶包络谱均值与扁疤长度之间的关系。其中图15对应的是列车以过超高状态通过曲线;图16对应的是列车以理论超高状态通过曲线;图17对应的是列车以欠超高状态通过曲线。
图15~图17表明,曲线线路不同地段前4阶包络谱均值与扁疤长度之间也呈线性关系,其斜率与直线线路的相近。但相同包络谱均值对应的扁疤长度与直线线路对应的扁疤长度之间存在偏差, 其主要是由于线路工况导致的。相较于直线线路,曲线线路轮轨之间的动力作用关系更加复杂,轮轨力存在着较大差别,因此在识别过程中会与直线线路上的识别结果存在一定偏差。同时曲线线路本身也较为复杂,缓和曲线与圆曲线的曲率、长度以及超高等因素都会导致识别偏差的产生。因此应对曲线地段识别的扁疤长度进行修正。
内轨侧缓和曲线和圆曲线处识别的扁疤长度与直线线路的偏差较小,而外轨侧偏差较大。其中,外轨侧圆曲线地段的识别偏差最大。因此对车轮扁疤进行全线不间断识别监测时,只需对曲线外轨侧进行修正。表4为由图15到图17得出的外轨缓和曲线和圆曲线车轮扁疤识别偏差。

表4 曲线外轨侧车轮扁疤识别偏差Tab.4 Outside rail curve wheel flat recognition deviation
由表4可以看出,无论是在欠超高、理论超高还是过超高地段,外轨缓和曲线线路识别的扁疤长度比基准大3~4 mm;外轨圆曲线线路识别的扁疤长度比基准大7~10 mm。因此当列车通过曲线地段时,对外轨缓和曲线地段应减去3~4 mm,对外轨圆曲线地段应减去7~10 mm进行修正。
6 结 论
本文提出了一种采用变分模态分解(VMD)的高速铁路车轮扁疤智能识别算法。通过车辆—轨道耦合动力学模型模拟得到不同车速、不同曲线线路的轮轨力随机响应,通过VMD分解后对IMF4 ~ IMF10进行重构和包络谱分析,研究了曲线地段使用该算法识别车轮扁疤的适应性,得到以下主要结论:
(1) 与传统扁疤识别方法相比,通过VMD分解并重构后的信号剔除了与扁疤冲击无关的分量,更直观地反映了冲击。
(2) 重构后信号的包络谱显示,不同列车速度对应的扁疤冲击倍频与包络谱各峰值处频率相一致,误差率不超过0.4 %;扣件支撑倍频与理论冲击频率误差率不超过0.09 %,说明本算法具有较高的识别精度。
(3) 不同列车速度、不同曲线线路下,正常车轮与扁疤车轮对应的包络谱差异明显,对10 mm以上的车轮扁疤可以准确识别。
(4) 为了对车轮扁疤进行全线不间断识别监测,应以直线地段包络谱均值与扁疤长度之间的线性关系为基准,对曲线外轨侧识别的扁疤长度进行修正:外轨缓和曲线地段应减去3~4 mm,外轨圆曲线地段应减去7~10 mm。对于不同速度、不同轨侧和不同曲线线路条件下的车轮扁疤,可以通过该线性规律判别出扁疤的长度,实时跟踪、预测扁疤长度的变化过程。

