一类考虑温度效应的截面插值梁模型

潘成浩， 陈国平,2， 何 欢,2

(1. 南京航空航天大学 机械结构力学及控制国家重点实验室， 南京 210016；2. 南京航空航天大学 振动工程研究所， 南京 210016)

承受横向载荷而受弯的构件称为梁。它是生产生活中常见的结构之一，也是工程实际中广泛采用的基本构件之一。常见的梁结构可以分为实体梁和薄壁梁两大类：实体梁变形以弯曲为主，薄壁梁变形以弯曲和扭转为主。传统的梁理论本质上是将三维的实际梁结构基于一定的假设，通过对梁的轴线和截面分别进行一定的处理，最终转化为一维问题，以此简化计算。由此建立的梁理论有经典梁理论(Euler-Bernoulli梁理论)、一阶剪切变形理论(Timoshenko梁理论)[1]以及高阶剪切变形理论(Reddy三阶梁理论)等。这些梁理论只适用于一定的范围，有一定的局限性。如Euler-Bernoulli梁理论适用于受剪切变形影响较小的细长梁的求解问题，但其忽略了横向剪应力和横向剪应变的影响，不适用于短梁、复合材料梁、夹层结构以及梁的振动等问题。Timoshenko梁理论[2]考虑了梁的弯曲变形引起的转动惯量和梁的剪切变形，适用于短深梁，但仍存在能量不自洽、剪切自锁等问题。许多学者对于上述三种理论进行了深入研究：Newmark[3]、Levinson[4]、Li[5]、周倩南[6]、何欢等[7]、Wan等[8]针对这些局限性，考虑剪切滑移、横截面翘曲，提出了多种新的梁模型。经典梁理论由于采用了平截面假设，所以在截面变形的描述上有很大的不足，例如机翼在复杂载荷作用下翘曲变形较大，传统的梁理论不能反映复杂的截面变形。此外，针对复杂截面而言，传统的梁理论不能精确地描述截面的几何形状，由此对力学特性的描述就不够精确。商业有限元软件在处理复杂截面、复杂工况的梁结构时推荐采用实体单元，但是这又带来自由度增加计算规模增大的问题。

为此，本文提出一种基于截面插值的考虑温度效应和截面形状的梁的有限元单元模型。该模型摒弃之前梁理论的刚性轴假设和中性轴假设，将梁单元分为在截面上的截面特征点和沿轴向的单元节点，如此就可以由轴向单元节点的位移经插值得到任意一个截面上截面特征点的位移，再由截面特征点的位移插值得到该截面内任意一点的位移，这样就得到了截面插值梁模型的位移场。经过这种方法得到的位移场能够很轻易地描述截面的形状，同时在面对温度梯度时，也能很好地反映不同温度带来的不同变形。再基于虚功原理得到单元刚度矩阵、温度刚度矩阵和质量矩阵，对结构进行静力分析和模态分析。

另外，热模态分析是研究结构的热振动和热颤振的基础。分析热模态关键是分析温度变化对结构的影响。而温度变化对结构的影响主要体现在两方面，一是温度变化影响材料的特性，例如在高温情况下某些金属材料的弹性模量会降低，影响结构的整体刚度。二是温度变化产生的热应力会形成初应力刚度，影响结构的刚度。国内外学者在这方面进行了大量的研究。吴晓等[9-12]研究了材料特性随温度变化后对结构振动的影响；Snyder等[13-15]则研究了热应力对结构振动的影响。Kehoe等[16-19]研究对比了这两方面各自对结构振动的影响。

针对提出的考虑温度效应的截面插值梁模型，本文同样研究了其热模态的计算，并与Nastran实体单元计算结果比较，验证模型的可靠性。

1 位移场的构造

本文中梁位移场的构造需要进行两步插值：第一步在截面特征点之间进行插值，第二步要在轴向节点之间进行插值。本文采用的插值方法均为拉格朗日多项式插值。

对于第一步插值采用二元拉格朗日多项式进行插值。根据在自身处二元拉格朗日插值多项式取值为1，在其他点处多项式取值0，并且所有插值多项式的和恒为1这个特点，可以很轻易地构造出插值函数。本文的插值函数也对应于传统单元的插值函数：三节点插值多项式对应于三节点三角形单元的形函数，四节点则对应于四节点矩形单元，九节点则对应于九节点矩形单元。图1为局部坐标系下的标准拉格朗日单元。

(a) L3

(b) L4

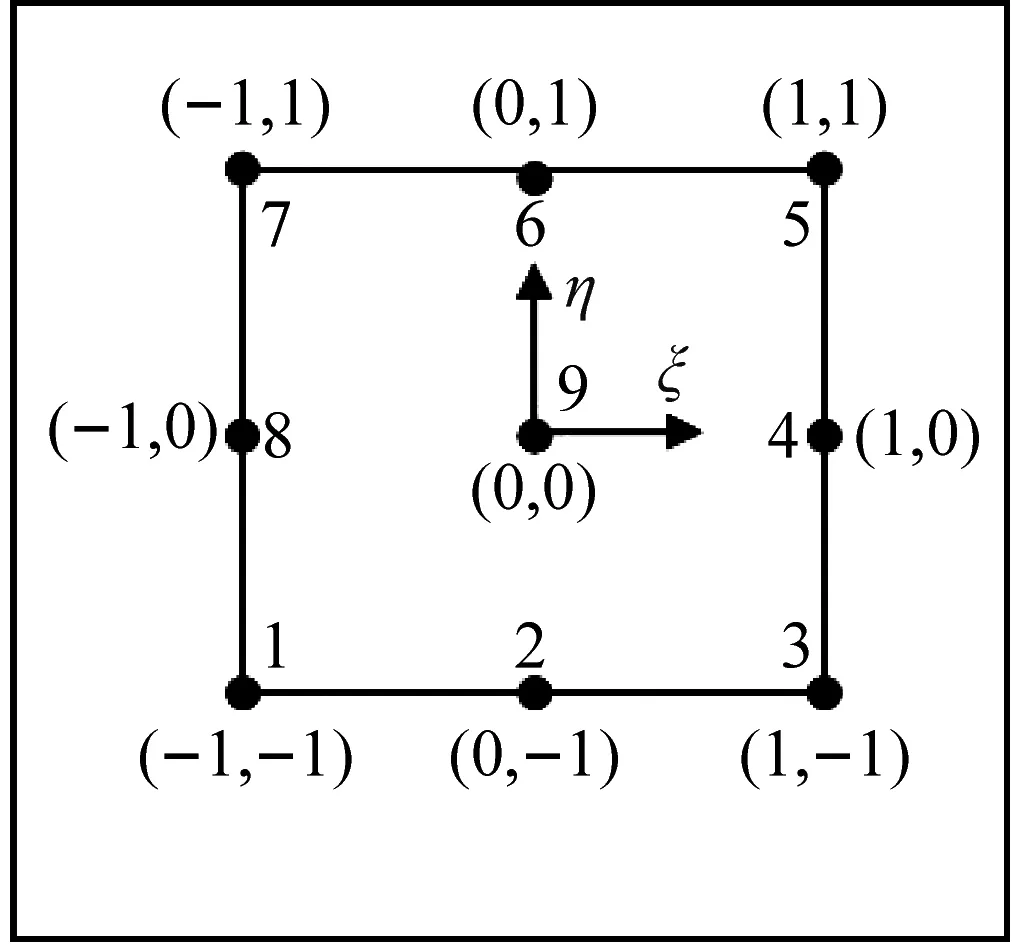
(c) L9图1 局部坐标系下的标准拉格朗日单元Fig.1 Standard Lagrange element in local coordinate system

由此可以得到对应的拉格朗日插值多项式

F1=1-ξ-η

L3:F2=ξ

(1)

F3=η

(2)

(3)

式中，ξk，ηk为截面特征点k的坐标。

对于第二步的插值直接采用一维拉格朗日插值多项式，对于n个节点的一维单元，Ni(y)可采用n-1次拉格朗日插值多项式，即

(4)

式中：n是单元轴向的节点数；y1,y2,…,yn是n个节点的坐标。

利用拉格朗日插值函数可以得到梁单元的位移场

u=FkNiuki,k=1,2,…,m,i=1,2,…,n

(5)

式中：u为单元内任意一点的位移向量；m为截面特征点数；n为轴向节点数；uki为轴向节点i所在截面内第k个截面特征点的位移向量

uki=[ukix,ukiy,ukiz]T

(6)

用矩阵来表示就是

u=FN·u′

(7)

其中：

(8)

(9)

在之后的计算中还需要根据已知的节点温度来插值得到单元中任意一点的温度，采用的插值方法和位移场的构建方法相同，故可以得到单元内任意一点的温度为

T=FkNiTki

(10)

式中，Tki为轴向节点i所在截面内第k个截面特征点的温度。同样可以用矩阵表示

T=FN′·T′

(11)

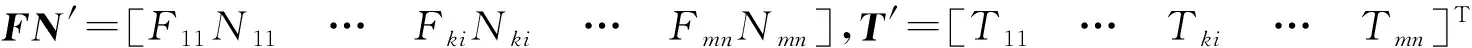
2 有限元分析

2.1 应变和应力

将式(7)代入几何方程，可以导出单元总应变与单元节点位移的关系，即

ε=Lu=L·FN·u′

(12)

式中，L为微分算子矩阵

(13)

温度变化在单元内产生的应变，即初应变为

(14)

式中，α为线膨胀系数。

将式(12)和式(14)代入热弹性理论下的物理方程，可以导出单元应力与单元节点位移、单元节点温度的关系，即

σ=D-1(ε-εT)=D-1(L·FN·u′-αFN′·

T′·a)

(15)

式中：ε为总应变，是弹性体在外载荷作用下产生的弹性应变和初应变εT两者之和；D为弹性矩阵

(16)

式中：ν为泊松比；E为弹性模量；G为剪切模量。

2.2 单元刚度矩阵和质量矩阵

假设单元发生虚位移，则虚位移和相应的虚应变为

δu=FN·δu′

(17)

δε=Lδu=L·FN·δu′

(18)

故由虚功原理可知，单元中内力所做的虚功与外力所做的虚功总和为零

δWI+δWE=0

(19)

单元中内力所做的虚功为

(20)

单元中外力所做的虚功为

δWE=δWext+δWine

(21)

式中：δWext为外力(除去惯性力)所做虚功；δWine为惯性力所做虚功

(22)

(23)

式中：PV为作用在单元上的体积力；PS为作用在单元上的面力；PP则为集中力；ρ为单元体的密度。

令

(24)

整理式(17)至式(24)，可得

(25)

化简可得

(26)

通过上式可计算出热应力。

2.3 单元组集

对于截面插值梁单元的单元组集过程和传统有限元计算的过程大致相同，都是将矩阵中的各元素按照结构节点自由度排列顺序“对号入座”叠加而成。但与传统梁单元不同的是，截面插值梁单元不仅能在梁的轴向方向上组集，还能在截面内通过共用特征点的方式组集。这能很准确地描述复杂的截面形状，同时也能通过局部增加截面插值梁单元的密度来提高有限元计算的精度。

2.4 求解热模态

利用计算得到的热应力推导热模态的计算公式，这需要更新刚度矩阵，把热应力的影响考虑进去。考虑在实际情况下，梁模型在受热后主要受力为轴向的热应力σaxial，故类比于受轴力作用的梁，受热梁振动时的内力虚功包括微小振动带来的虚功和考虑由轴向热应力引起的横向剪切力在对应剪应变上做的虚功。而由轴向热应力引起的横向剪切力为：σaxial·usec1,y和σaxial·usec3,y对应的剪应变为δusec1,y和δusec3,y。其中下标“sec1”，“sec3”表示截面内的两个坐标轴方向，下标“,y”表示对y求偏导。则内力虚功变为：

FNsec3,ydV)u

(27)

则更新后的刚度矩阵为

(28)

最后利用更新后的刚度矩阵和质量矩阵就可计算得到热模态。

3 算例1

考察如图2所示的矩形截面梁，其尺寸为：a=20 mm，b=100 mm，长度L=2 000 mm。弹性模量E=200 GPa，泊松比ν=0.25，材料密度ρ=2 700 kg/m3，热膨胀系数α=11×10-6。该梁的约束情况为一端固支一端自由。

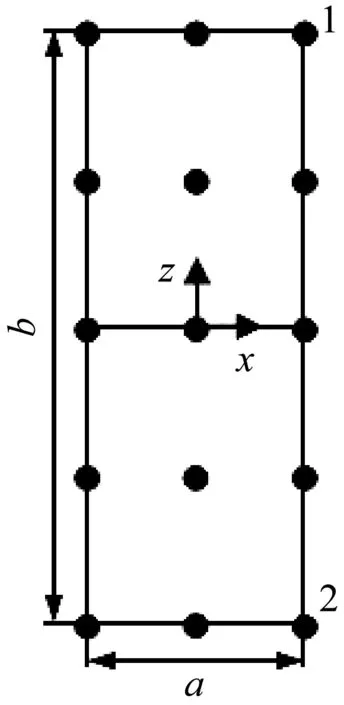
图2 矩形截面梁Fig.2 Diagram of rectangular section beam

对矩形截面梁进行单元划分，在截面上划分两个单元，每个单元截面采用九点插值(L9),轴向取四个节点。同时在矩形截面梁上作用一个温度梯度T=180(20z+1)℃。利用上面的公式进行单元分析，将得到的结果与Nastran软件中的Solid单元计算结果进行比对分析，注意Solid单元在每个特征点处均有节点，以此保证截面插值梁单元与Solid单元有相同的自由度。

图3给出了随着轴向单元数的增加，截面插值梁单元2L9与Solid单元自由端挠度的变化。从图中可以看出，截面插值梁单元的挠度计算结果比Solid单元的挠度计算结果更快收敛。由此可以看出截面插值梁模型在计算细长梁时比Solid单元更快捷，更有优势。

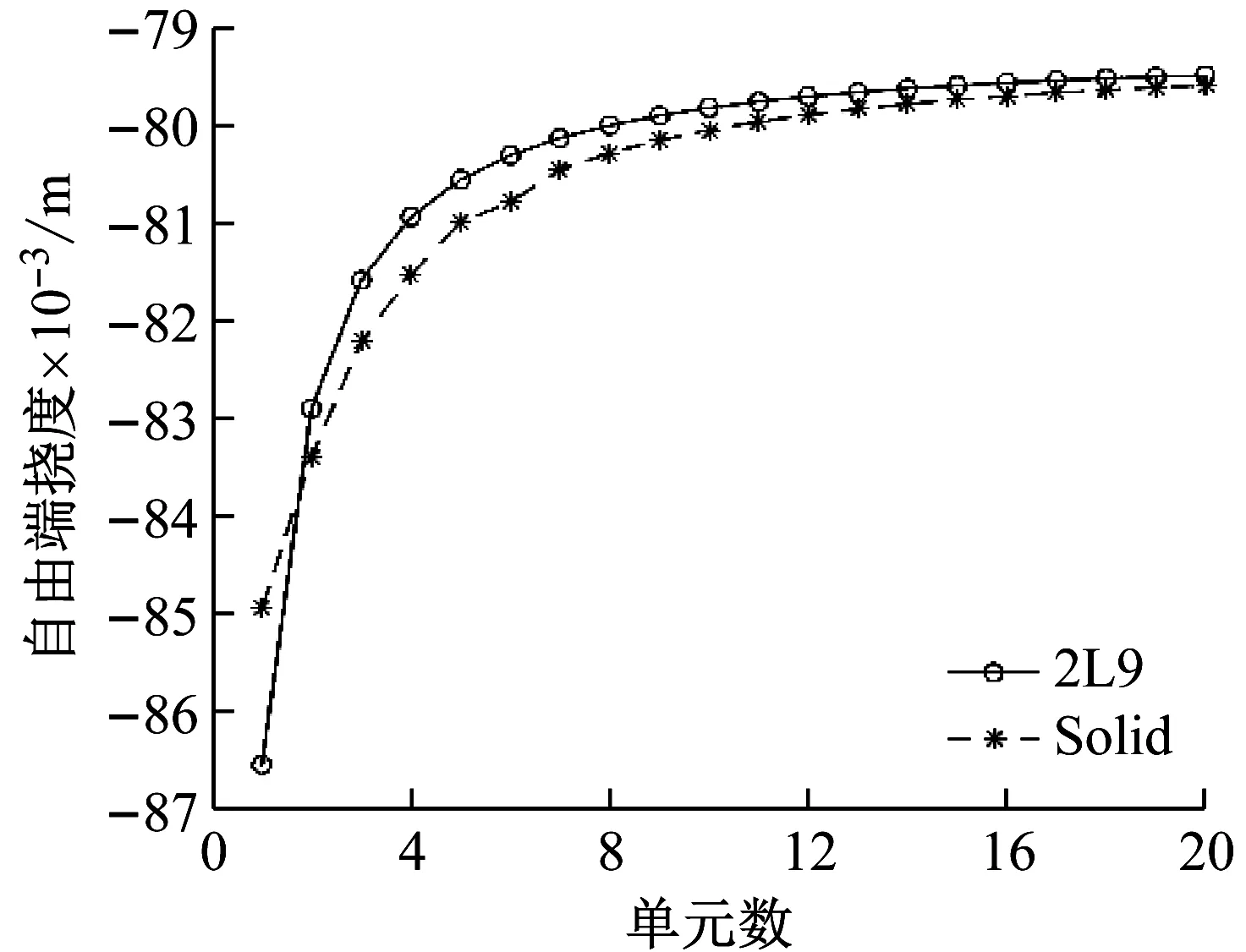
图3 自由端挠度随轴向单元数变化曲线Fig.3 Deflection varies with axial element number

4 算例2

为验证截面插值梁模型对复杂截面的处理的准确性，以图4所示的工字梁为例进行计算。其尺寸为：W=100 mm，H=100 mm，t1=8 mm，t2=5 mm，长度L=1 000 mm。材料的弹性模量E=210 GPa，泊松比ν=0.29，密度ρ=2 700 kg/m3，热膨胀系数α=11×10-6。

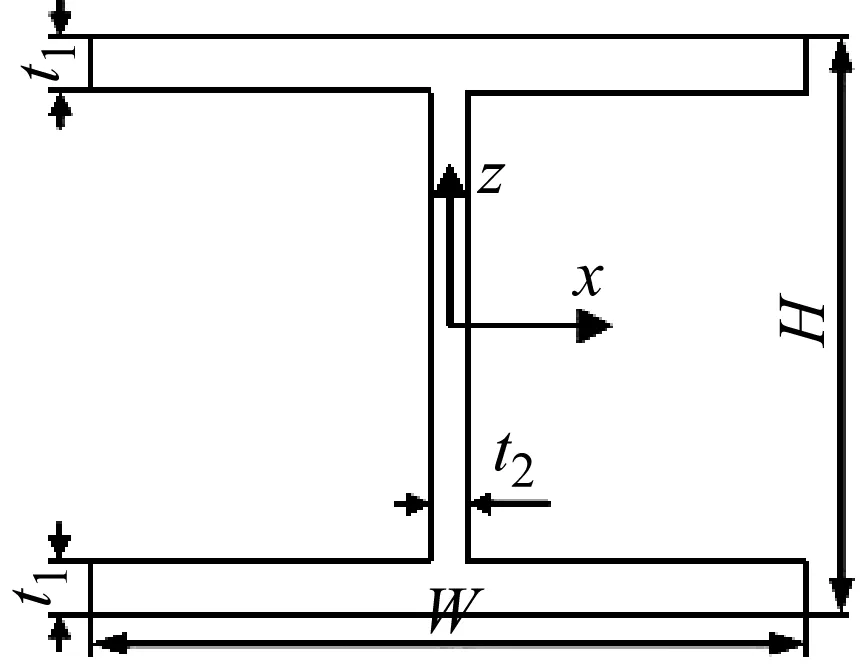
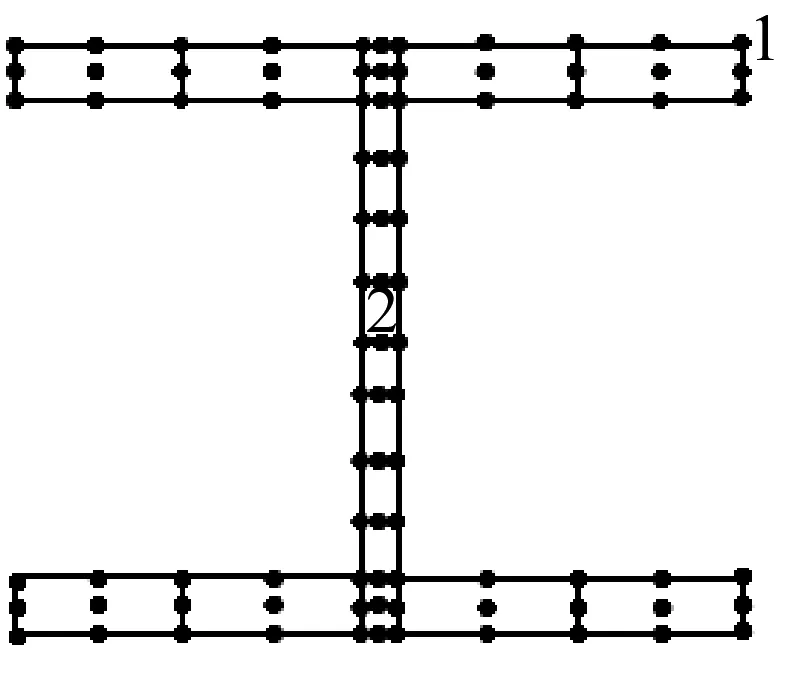
图4 工字梁截面Fig.4 I-shaped profile diagram

对工字型截面采取如图4的单元划分形式，共划分14个单元，每个单元的截面都采用九点插值(L9)，同时在轴向上划分20个单元，每个单元轴向取四个节点。该梁的约束情况为两端固支。

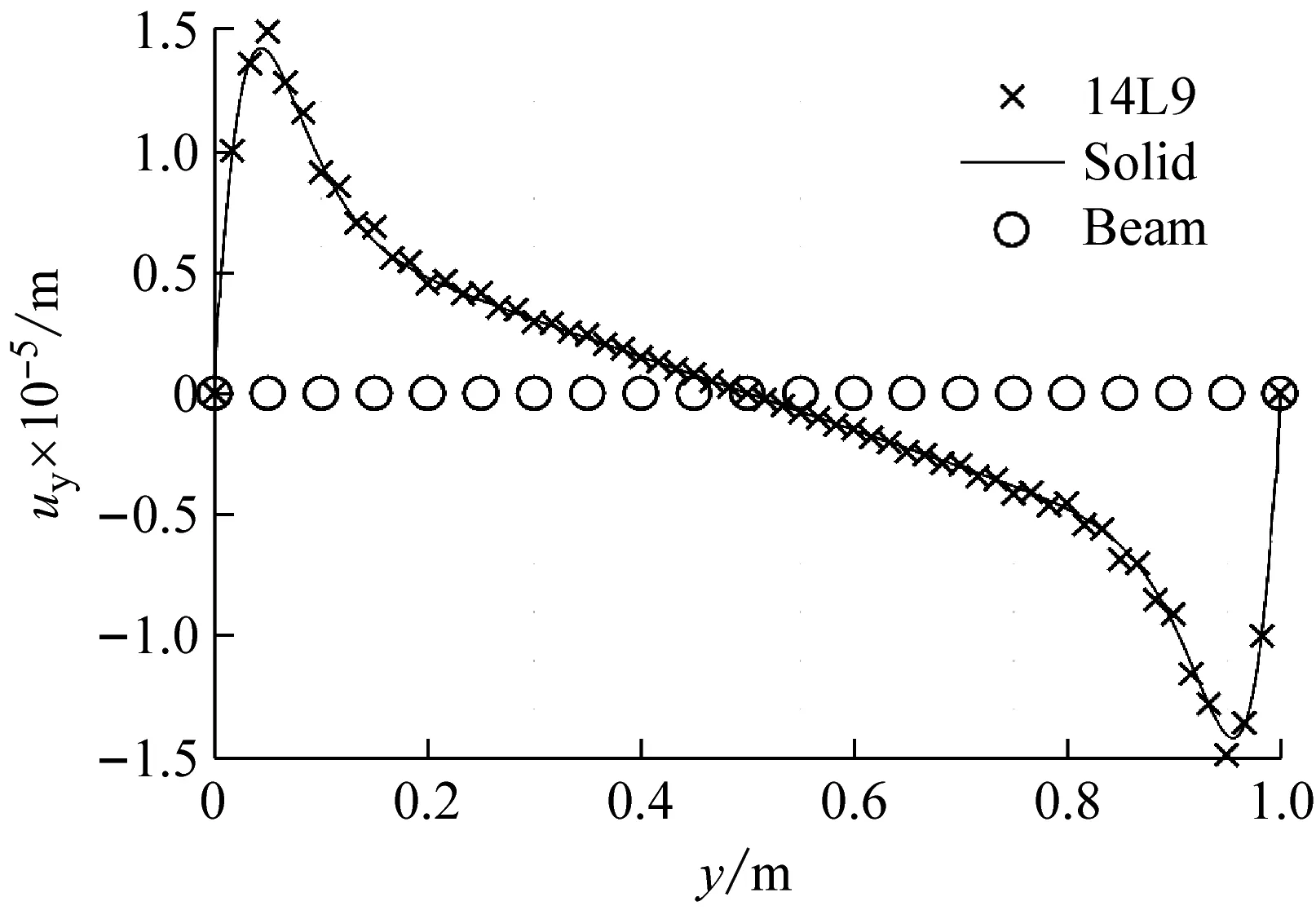
图5(a)是在工字梁上作用均匀温度场T=10 ℃的截面变形图(变形放大1 000倍)。图5(b)是在T=100 ℃时的截面变形图(变形放大100倍)。图5(c)是在T=1 200z+60 ℃时的截面变形图(变形放大100倍)。图6(a)和(c)分别是均匀温度场T=100 ℃和非均匀温度场T=1 200z+60 ℃下点1(0.05,0,0.05)所在轴线的x向挠度，图6(b)和(d)分别是均匀温度场和非均匀温度场下点2(0,0,0)所在轴线的y向位移。均匀温度场下比较了截面插值梁模型(14L9)、Nastran的Solid单元和Beam单元的计算结果；而由经典梁理论导出计算的Beam单元无法施加非均匀温度场T=1 200z+60 ℃，所以非均匀温度场下只比较了截面插值梁模型(14L9)和Nastran的Solid单元的计算结果。从图中可以看出无论是作用均匀温度场还是非均匀温度场，截面插值梁模型的计算结果与Solid单元计算结果一致，精度很高，与Beam单元相比，截面插值梁模型能更好地反映梁截面上的变形。

(a) T=10 ℃

(b) T=100 ℃

(c) T=1 200z+60 ℃图5 截面变形图Fig.5 Cross-section deformation

(a) 点1，T=100 ℃

(b) 点2，T=100 ℃

(c) 点1，T=1 200z+60 ℃

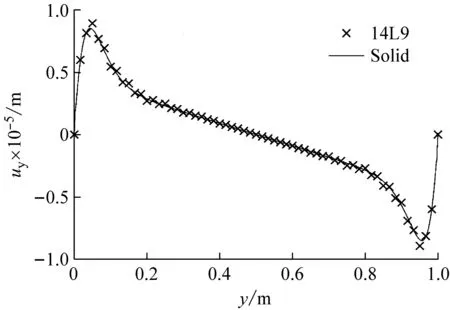
(d) 点2，T=1 200z+60 ℃图6 各向位移曲线图Fig.6 The displacement curve

5 算例3

同样考虑算例1的矩形截面梁，梁长度改为L=1 000 mm，在截面上还是划分两个单元，在轴向上划分20个单元。约束情况改为两端固支。另外用商业有限元软件Nastran里的Solid单元和Beam单元进行建模，建模中轴向取相同的节点数。

5.1 静力学分析

静力学分析中考察的情况是在矩形截面梁上作用温度载荷，分为两种工况，第一种是均匀温度场T=100 ℃，第二种是非均匀温度场T=1 800z+90 ℃。图7是点1(0.01,0.05,0.467)(即截面右上角顶点)所在截面的变形图对比(变形放大100倍)。图8是点1和点2(0.01,0,-0.05)(即截面右下角顶点)所在轴线的轴向应力对比。表1是两种温度场下不同建模方法计算的点1的位移和应力值，从图中可以看出截面插值梁模型不仅准确地描述了截面变形，也能准确地计算轴向应力，尤其是在两端约束处的应力激增位置，截面插值梁模型仍可以准确反映这种变化。

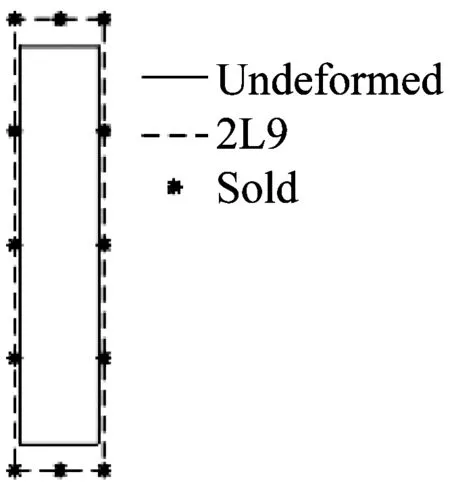
(a) T=100 ℃

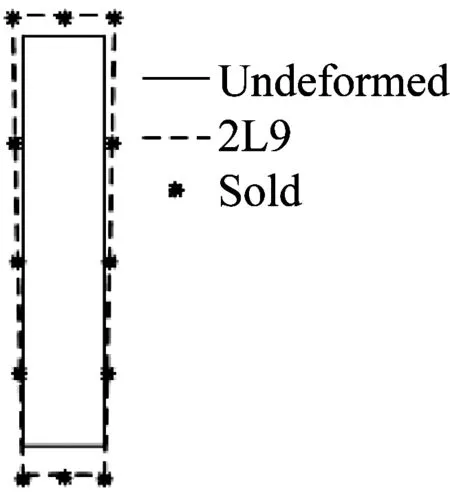
(b) T=1 800z+90 ℃图7 截面变形图Fig.7 Cross-section deformation

(a) T=100 ℃

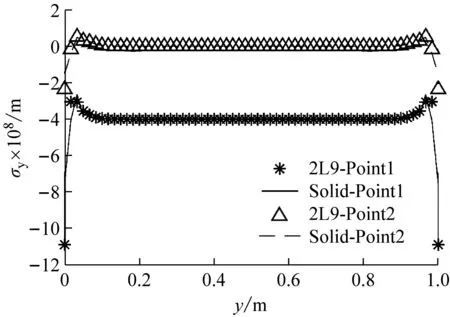
(b) T=1 800z+90 ℃图8 不同温度下正应力分布曲线Fig.8 Positive stress distribution curves under different temperatures

表1 点1位移和应力结果Tab.1 Displacement and stress result of Point 1

5.2 动力学分析

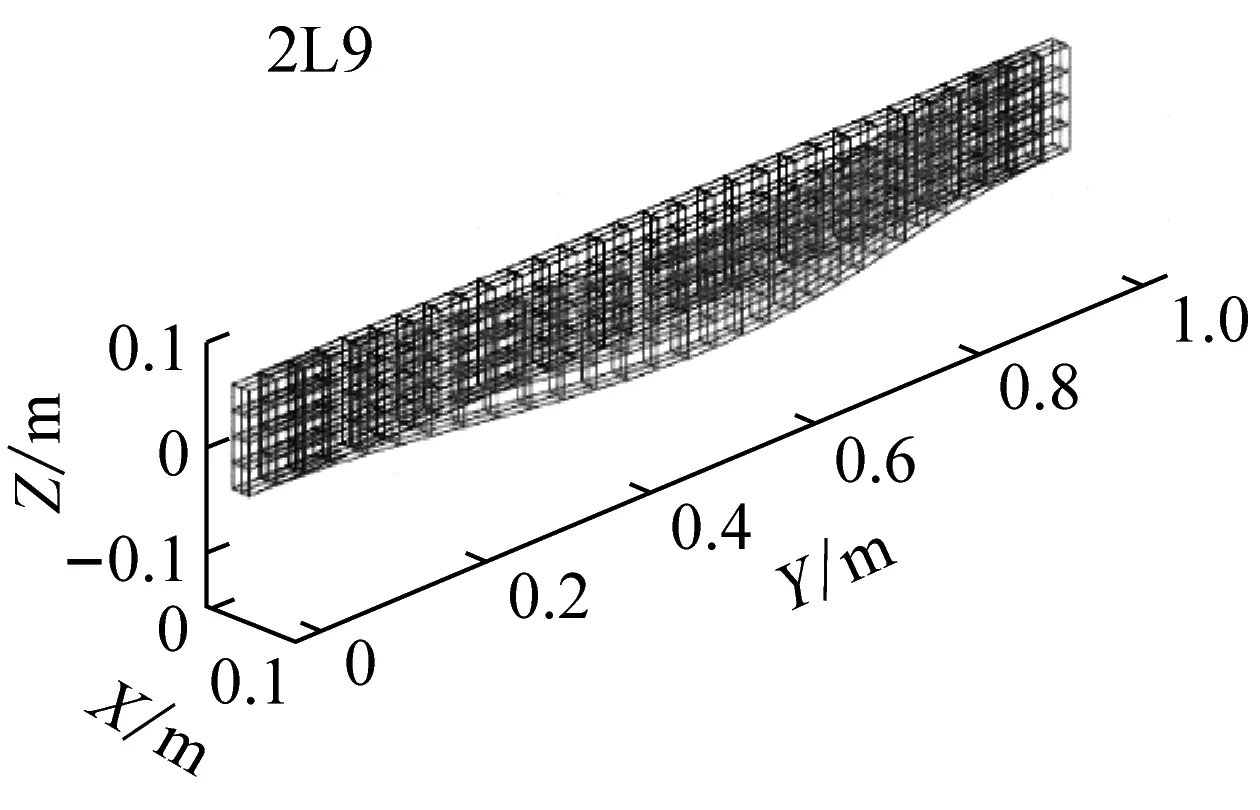
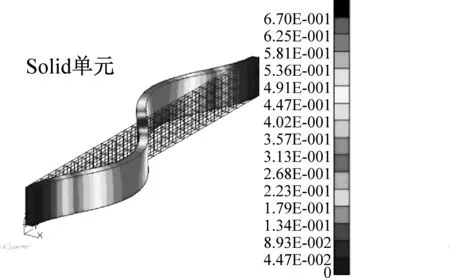
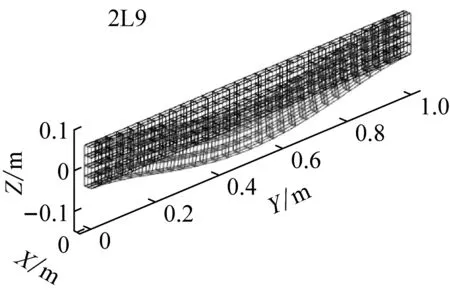
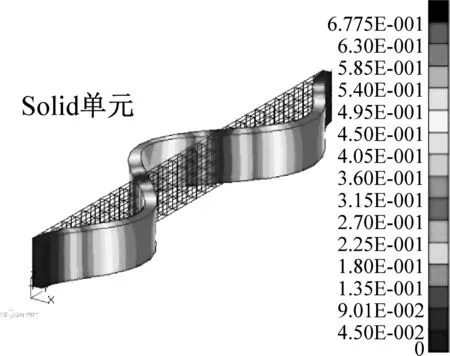
对矩形截面梁进行模态分析，表2是不考虑温度的模态对比。表3是考虑均匀温度场的模态对比。表4是考虑非均匀温度场的模态对比。从表中可以看出，Beam单元无法得到扭转模态。而截面插值梁单元则不会缺失扭转模态，而且其余模态的精度相对更高。图9给出了Solid单元和截面插值梁单元的模态振型对比(考虑非均匀温度场)，通过振型比较可以发现，两种方法的模态振型是一致的。图10是对应的MAC置信度柱状图，对角线上前10阶的模态置信度均大于0.99，说明截面插值梁单元的模态计算结果与Solid单元的计算结果吻合程度很好。

(a) 第1阶

(b) 第2阶

(c) 第3阶

(d) 第4阶

(e) 第5阶

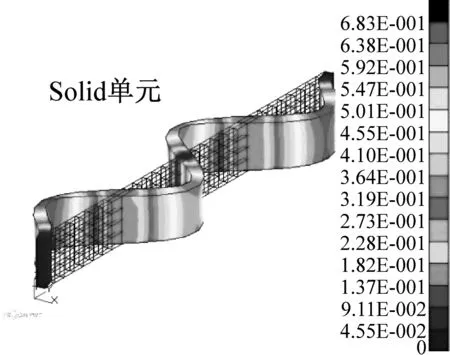
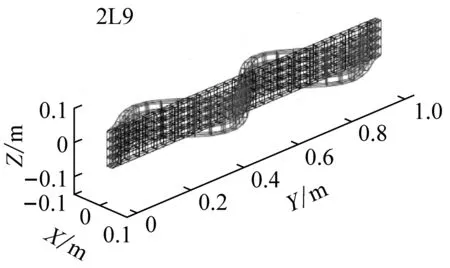
(f) 第6阶图9 非均匀温度场下模态振型对比Fig.9 Comparison of mode shapes under non-uniform temperature

图10 非均匀温度下MAC柱状图Fig.10 MAC histogram under non-uniform temperature

表2 不考虑温度的模态结果Tab.2 Modal results regardless of temperature

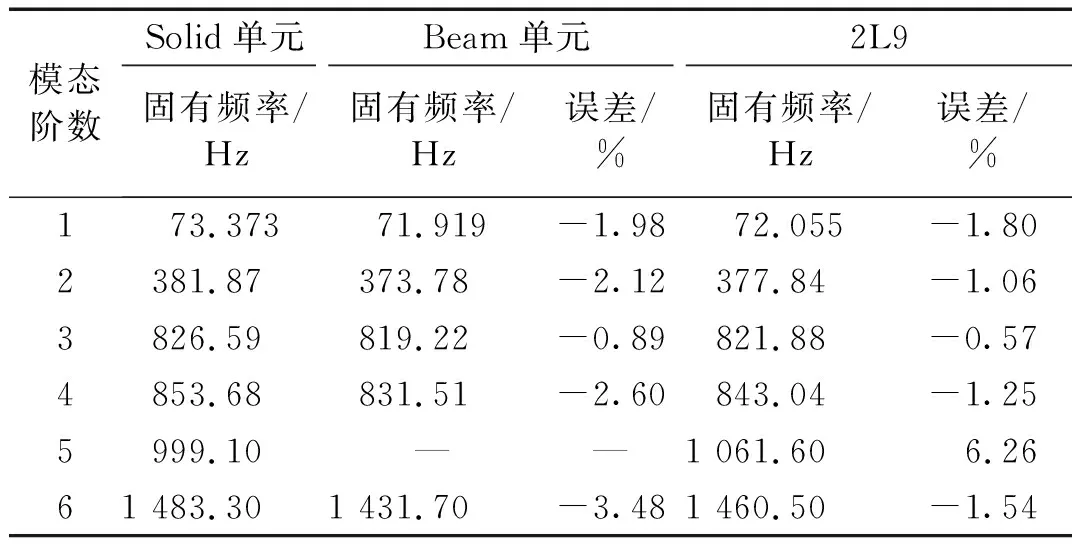
表3 均匀温度场下模态结果Tab.3 Modal results under uniform temperature

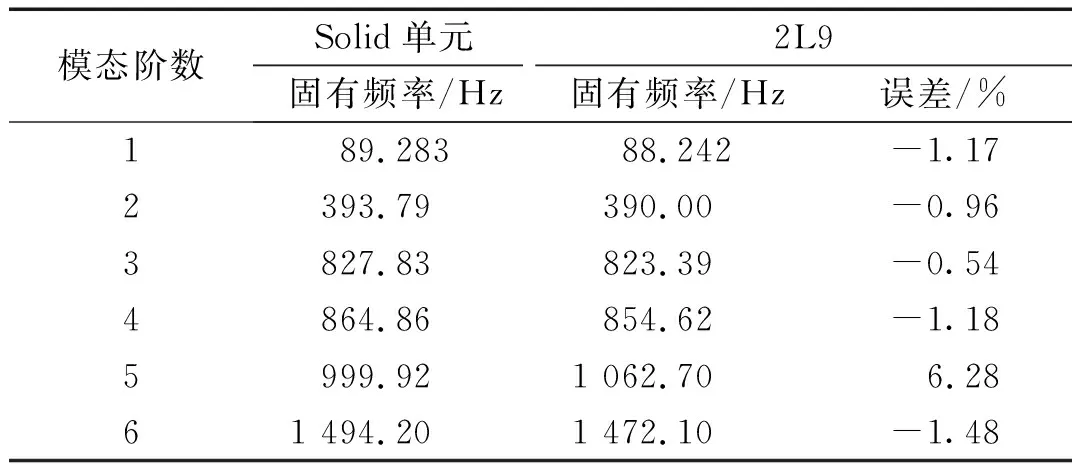
表4 非均匀温度场下模态结果Tab.4 Modal results under non-uniform temperature

从静力学分析与动力学分析结果来看，截面插值梁模型可以很好地应用于复杂截面梁在复杂温度情况下的响应分析。

6 结 论

本文提出了一种基于截面插值的空间梁模型，并研究了在考虑温度效应的情况下模型的运用。与传统梁模型相比，截面插值梁模型能很好地反映截面内的各种情况，比如截面的变形、截面内的温度梯度、截面的复杂形状，有着更高的计算精度。另外与Solid单元相比，在处理细长结构上，截面插值梁模型需要更少的节点，更少的自由度，同时能保证计算结果的精度与可靠性。