大跨度悬索桥吊索风致振动多重调谐阻尼减振技术研究

柴小鹏， 荆国强， 吴肖波

(1.桥梁结构健康与安全国家重点实验室，武汉 430034; 2.中铁大桥科学研究院有限公司，武汉 430034)

大跨度悬索桥吊索长细比大、阻尼小、基频低，在复杂风荷载激励下容易发生复杂的多模态振动问题，而且随着跨度的增加愈加明显。已建成的明石海峡大桥、英国塞文桥、丹麦大贝尔特东桥、我国的西堠门大桥、南沙大桥的坭洲水道桥和大沙水道桥均出现过风致振动问题。其中，西堠门大桥主跨为1 650 m，吊索为骑跨式钢丝绳吊索，其振动形式主要为低阶大幅振动、甚至出现过碰索现象，通过安装刚性分割器控制了低频大幅振动，但高频微幅振动仍有出现[1-2]。南沙大桥吊索为销铰式高强钢丝吊索，施工期吊索主要表现为中高频的振动，通过综合采用摆式杠杆阻尼器、冲击阻尼器、MTMD进行控制，减振效果明显[3-4]。由于MTMD无需与桥面连接，通过频率调谐使惯性质量响应放大，减振效果明显，具有广泛的推广价值[5-8]。

在建的主跨1 666 m的深中通道伶仃洋大桥[9]、主跨为1 760 m的南京仙新路长江大桥[10]，主跨2 023 m的土耳其1915恰纳卡莱大桥[11]，跨度更大、吊索更长，且风环境复杂，其减振要求更加严格。另外悬索桥吊索实际振动模态复杂多样，MTMD虽然已有实践应用，但是MTMD的设计参数优化、吊索安装位置优化、不同主频的振型参与系数影响等因素都需要进一步研究。

为此，本文以南沙大桥为工程背景，通过分析吊索实际发生振动的频率分布、振型等振动特性，确定阻尼减振目标，建立吊索-MTMD理论分析模型，优化TMD的参数，分析TMD对吊索多主频的阻尼减振效果，利用MTMD实现对吊索多主频的全覆盖，最后考虑MTMD的振型参与系数，对MTMD的安装位置进行优化，达到吊索风致振动的减振目标。

1 大跨度悬索桥吊索振动特性实测分析

南沙大桥包括两座主航道桥，分别为主跨1 688 m的坭洲水道桥和主跨1 200 m的大沙水道桥，大桥整体布置如图1所示。施工期间60 m以上的长吊索均发生了明显的振动，通过实测分析，其主要特征为：

图1 坭洲水道桥和大沙水道桥总体布置Fig.1 Overall arrangement of Nizhou Waterway Bridge and Dasha Waterway Bridge

(1) 吊索的振动以中高频为主，不同吊索实测频率覆盖范围为5～20 Hz，表1为典型吊索的振动频率、对应阶次及振动加速度幅值统计表。

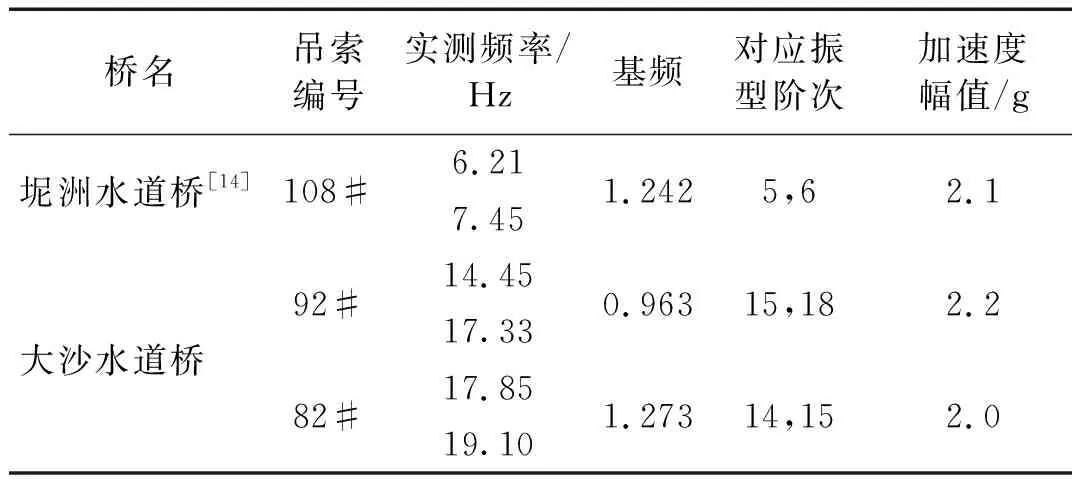
表1 南沙大桥吊索实测振动响应Tab.1 Hanger cables vibration response of Nansha Bridge

(2) 每个吊点并列双(三)吊索的振型组合复杂，每隔40 m加设一道刚性减振架后，吊索仍出现了顺桥向的同步振动[12]、异步振动，和横桥向的同步和异步振动。

(3) 吊索竖直布置，其风致振动的主要表现为涡激振动，根据汪正兴[13]的研究，控制涡激振动所需的阻尼对数衰减率δ达到1%～1.5%。

由于每个吊点有并列双索或者三索，组合之后模态复杂。如果专注于将单根吊索独立控制，并列索的组合振型亦会得到控制，因此将南沙大桥吊索阻尼减振目标确定为：通过安装MTMD，使单根吊索5～20 Hz振动的模态对数衰减率δ大于1.5%。

2 吊索-MTMD理论分析模型

吊索设置n个TMD的多重质量调谐阻尼器振动系统简化模型如图2所示。

(a) 构造图

(b) 力学简图图2 吊索-MTMD模型Fig.2 Hanger cable-MTMD model

吊索-MTMD系统动力学方程为

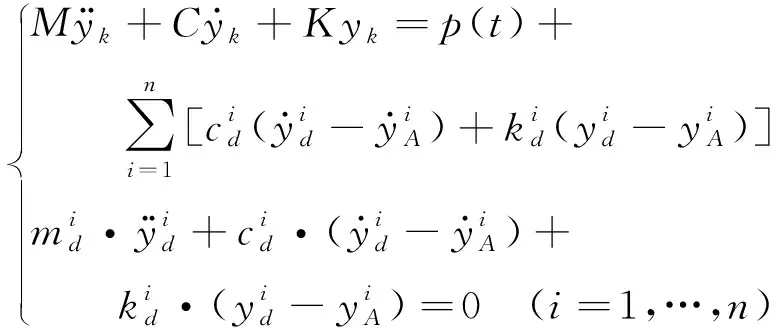
(1)

利用文献[13]的多目标满意度优化理论，可以对TMD阻尼器各参数进行优化。确定TMD的设计参数后，用式(2)评估吊索第k阶的模态阻尼对数衰减率δk

(2)

式中，Dk,max为共振时吊索第k阶的动力放大系数，其计算公式见式(3)。

(3)

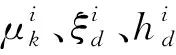
(4)

当MTMD处于k阶振型最大处时，振型参与系数为1，为了更好的发挥作用，阻尼器应尽量安装在各阶振型最大处，但对于吊索的振型特点而言，同一位置处对应不同振型阶次的振型参与系数是不同的。

3 MTMD阻尼器设计参数分析及优化

选取大沙水道桥92#吊索的单索为分析对象，其基本参数如表2所示。

表2 92#吊索单索参数Tab.2 92# Cable parameters

MTMD是由多个TMD组成，因此首先对单个TMD的参数进行优化，然后分析单个TMD对吊索多个振动主频的控制效果，优选出单个TMD的设计参数后，分析MTMD对吊索多个主频振动的控制效果，最后考虑吊索的初始阻尼和实际的振型参与系数，分析吊索安装MTMD后实际的阻尼参数。

3.1 TMD的参数优化分析

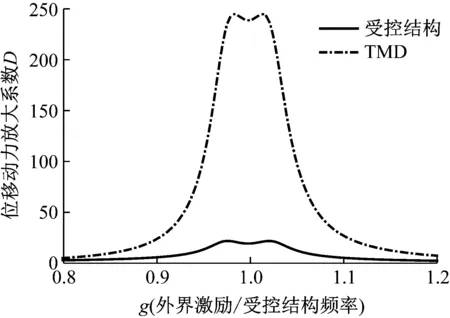
图3 吊索-TMD动力放大系数Fig.3 Cable-TMD dynamic magnification factor

从图3可知，优化后的最优阻尼比ξopt=4%，最优频率为17.3 Hz，在此最优参数下，吊索受控目标出现两个相等的动力放大系数峰值为21.8，TMD出现两个相等的动力放大系数峰值为244.8，根据式(2)计算得到吊索第18阶主频的附加阻尼参数δ=14.4%。

吊索实际的振动为多个主频，在上述TMD最优参数下，利用式(2)和式(3)，求解92#吊索5～20 Hz范围内的附加阻尼对数衰减率δ如图4所示，由于吊索有多个主频振动，需要提高单个TMD对多个主频的控制效果，图4中还列举了最优阻尼比和阻尼比增大后控制效果对比曲线。

图4 TMD不同阻尼比下吊索各主频附加阻尼参数Fig.4 Each main frequencies damping parameter for hanger cable under TMD different damping ratios

从图4可以看出，采用吊索单一受控频率下位移最小为优化目标的最优阻尼比ξ=0.04时，阻尼器对吊索17.33 Hz主频的附加阻尼效果最好，但对相邻主频的附加阻尼效果减小很快，其有效控制频率范围较窄；而将阻尼比提高至10%后，TMD对17.33 Hz振动的附加阻尼效果降低，而对相邻主频附加阻尼效果提高，有效控制范围变宽；当阻尼比从10%提高至15%时，依然具有上述变化趋势，但对受控主频的削弱较多，而对相邻频率的提升不明显，考虑TMD实际构造中钢绞线提供的阻尼比大约为10%，因此选择10%作为控制吊索用TMD的最优阻尼比。另外，单个TMD的频率覆盖范围有限，为了对5～20 Hz振动进行全覆盖控制，需要采取多个主频的MTMD方案。

3.2 MTMD对吊索多主频振动控制分析

采用MTMD实现吊索振动主频的全覆盖，是在不同主频各自覆盖一定频率范围的基础上，协同工作实现对吊索主频振动的覆盖。通过多次试算，为了有效抑制单根吊索5～20 Hz振动，需要4组不同主频的MTMD(实桥安装效果如图5所示)，其频率分别为f1=6.5 Hz、f2=9.5 Hz、f3=13.5 Hz和f4=18 Hz，4个TMD的单一效果和协同工作提供给吊索各主频振动的阻尼对数衰减率δ如图6所示。

图5 MTMD实桥安装效果Fig.5 Installation effect of MTMD in real bridge

图6 MTMD对吊索各主频阻尼参数Fig.6 Cable main frequencies damping parameter by MTMD

从图6可以看出，单一频率TMD的频率覆盖范围具有高阶宽、低阶窄的特点，通过4个TMD的协同工作方案，实现了吊索多模态振动覆盖的目的。

3.3 考虑实际振型参与系数的MTMD安装位置优化

在实际吊索阻尼减振中，阻尼器安装在某个固定位置，对各阶振型的振型参与系数是不同的，式(4)给出了吊索各阶振型参与系数的计算方法，根据现场实测，吊索初始阻尼参数δ=0.6%，安装4个主频的MTMD后，92#吊索的5～20 Hz阻尼对数衰减率δ变化趋势如图7所示。

图7(a)中MTMD安装在同一位移，其安装位置比分别为2.5%、3.8%、5%，对应的最大振型参与系数最大值出现在19.6 Hz(第20阶)、12.7 Hz(第13阶)和9.6 Hz(第10阶)，三种布置方案表现为：

(a) 统一安装位置对比

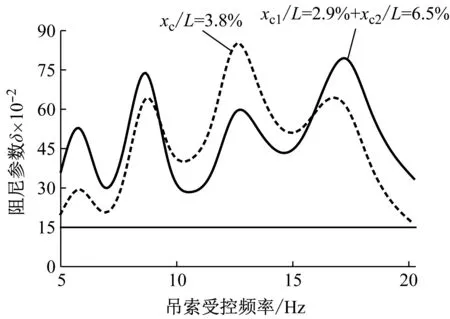
(b) 不同安装位置对比图7 不同安装位置比下MTMD对吊索各主频阻尼参数Fig.7 Each main frequencies damping parameter for hanger cable by MTMD under different installation position ratio

(1) 2.5%的安装位置比下，高频部分的效果更好、中低阶变差，5～7 Hz低于0.015的目标值，不满足要求；

(2) 5%的安装位置比下，中低频率的效果更好，16～20 Hz低于0.015的目标值，不满足要求。

(3) 3.8%的安装位置比下，中间频率范围的阻尼参数更好，低频和高频的效果变差，但均能满足0.015的目标值要求。

图7(b)中，将6.5 Hz和9.5 Hz的MTMD安装在位置比6.5%处，13.5 Hz和18 Hz的MTMD安装在位置比2.9%处，组合形成DMTMD，各阶频率对应的阻尼参数δ大于0.03，各阶综合性能优于将4个主频安装在同一位置处的效果。

3.4 不同长度的吊索MTMD

悬索桥的吊索，除过靠近桥塔最长的几根吊索外，其余吊索型号一致，索力也基本差不多，差别仅在于索长不同，对于不同索长的MTMD参数设计，需要研究上述理论分析的适用范围，是否每根吊索都需要单独进行优化分析。

吊索的第k阶频率见式(5)

(5)

定义Lk为吊索的第k阶模态有效索长，其物理意义如图8所示。

图8 吊索第k阶的模态有效索长Lk示意图Fig.8 Modal effective cable length Lk schematic diagram

将式(5)变换为关于Lk的表达式，为

(6)

从式(6)可知，当不同长度吊索的型号相同，索力接近，受控频率范围相同时，其模态有效长度接近，则MTMD的安装位置xc也接近。所以，悬索桥吊索采用MTMD减振时，目标控制频率范围相同的前提下，可以采用同类型号的MTMD，设计及参数及安装位置可统一设计。

4 结 论

采用数值方法，建立吊索-MTMD减振系统，研究MTMD控制吊索多模态振动的设计参数优化、安装位置优化，得到了如下主要结论：

(1) 以单一主频控制效果最优为目标的TMD优化阻尼比为4%，对临近主频的覆盖范围较窄，不适用吊索的多模态控制；将阻尼器提高至10%后，频率覆盖范围增加，而继续增加阻尼比，综合效果不明显；优选4个主频的MTMD，实现吊索5～20 Hz受控主频的全覆盖。

(2) 将6.5 Hz和9.5 Hz安装在位置比6.5%处，13.5 Hz和18 Hz安装在位置比2.9%处，各阶频率对应的阻尼参数δ大于0.03，各阶综合性能优于将4个主频安装在同一位置处的效果。

(3) 针对不同长度吊索，其索力、型号、受控频率范围接近时，MTMD的设计参数和安装位置可统一采用。