基于一维卷积神经网络的超声导波管道裂纹识别方法

唐若笠， 张尚煜， 伍文君

(武汉理工大学 船海与能源动力工程学院，武汉 430063)

在船舶运输、石油化工等工程现场，各类工业管道往往服役环境复杂，在运行过程中不可避免地会产生不同程度和类型的损伤失效。其中，管道表面裂纹是最为常见的损伤形式之一[1]。这种损伤一旦加剧便会引起管道的泄露甚至断裂，这不仅危害到整个工业自动化系统的安全、稳定运行，甚至会造成生态环境污染等严重后果。为此，及时、准确地发现管道的裂纹缺陷，对管道的安全运行起着决定性作用[2]。在许多情况下，传统的目视检查无法在缺陷形成的初始阶段检测到形态细微的各类缺陷[3]。相比之下，超声导波由于具有易激发、可长距离传输、可大面积扫描，以及对细微缺陷敏感等优点[4]，被认为是最可行的缺陷检测方法之一。然而，由于超声导波具有多模态以及频散等复杂特性[5]，基于人工方法对导波的缺陷回波信号进行分类诊断同样具有较大的复杂性。为此，基于数据驱动的超声导波缺陷识别方法在管道结构健康监测领域引起了国内外学者的广泛关注。

主流的缺陷识别方法是将原始数据进行特征提取以得到多维特征参数，随后采用基于数据驱动的方法达到预期的分类结果。Cruz等[6]采用离散傅里叶变换(discrete Fourier transform, DFT)、离散余弦变换(discrete cosine transform, DCT)和离散小波变换(discrete wavelet transform, DWT)进行特征提取，以多层感知器(multi-layer perception, MLP)神经网络作为机器学习(machine learning, ML)学习分类器对钢板进行焊接缺陷分类。Li等[7]采用希尔伯特变换(Hilbert transform, HT)、功率谱密度(power spectral density, PSD)、快速傅里叶变换(fast Fourier transform, FFT)和小波分维(wavelet fractal dimension, WFD)进行特征提取，以支持向量机(support vector machine, SVM)作为机器学习方法识别钢板缺陷类型。Liu等[8]采用时频分析(time-frequency analysis, TFA)工具箱和5种熵值进行特征提取，利用二进制粒子群优化算法选择最佳特征子集，基于最小二乘支持向量机(least squares support vector machine, LS-SVM)构建分类模型。近年来，随着深度学习技术的兴起，传统机器学习方法正逐渐被深度学习算法所取代，虽然经典的机器学习方法只需要较少的数据集和较低的计算成本[9]，但深度学习算法在不需要数据预处理的情况下实现了更高的预测精度。

近年来，国内外学者对不同管道缺陷的分类开展了大量研究，分类对象主要集中于腐蚀、凹坑、裂纹、焊接这4类缺陷。相比之下，已有研究对管道表面裂纹疲劳扩展程度的关注较少。本文将管道裂纹缺陷量化为5个等级指标，提出一种基于多尺度一维卷积神经网络(multi-scale one-dimensional convolutional neural network, MS-1DCNN)的管道裂纹缺陷等级分类方法。该方法可以直接将原始波形信号作为模型输入，无需任何针对波形信号的特征提取、预处理或后处理等额外操作，最大限度地减少原始波形信号中信息的损失，进而能够快速、准确地实现管道裂纹等级分类，从而对含缺陷管道进行准确的安全评估。

1 卷积神经网络

卷积神经网络(convolutional neural network, CNN)是一种著名的深度学习架构，其灵感来自于生物的自然视觉感知机制，最早被应用在图像分类中[10]。CNN与传统的神经网络相似，都是由输入层、隐藏层和输出层所组成。但不同的是，CNN的隐藏层包括卷积层、池化层和全连接层。卷积层是CNN网络的核心，在卷积层中引入局部感受野概念，通过设置不同维数和步长的卷积核(Kernel)，就可以对输入进行不同特征和尺度的特征扫描，进而实现从输入数据中直接提取特征[11]。卷积层之后通常为激活层，主要作用是将卷积层输出结果进行非线性映射，从而提高模型的泛化能力。池化层通常位于两个卷积层之间，可以进行不同形式的下采样，降低特征分辨率，得到抽象化的特征，从而减少模型中的参数量和计算量，并在一定程度上保留重要信息[12]。全连接层通常将各层的每一神经元通过一定的连接权逐一相连[13]。综上所述，卷积神经网络的具体框架结构如图1所示。

图1 卷积神经网络结构Fig.1 Convolutional neural network structure diagram

在过去的几年里，CNN在诸多工程技术领域都得到了广泛而成功的应用。其中，一维卷积神经网络(one-dimensional convolutional neural network, 1DCNN)通常用于分析一段固定长度的信号数据，其优点之一是可以使用大窗口尺寸的过滤器来提取更多的数据信息。1DCNN不需要繁琐的数据预处理，可直接将原始信号用作为模型输入，并能够在各种环境下保持较高的预测精度。Janssens等[14]基于卷积神经网络模型进行轴承故障诊断，与传统的人工特征提取方法相比，其故障诊断模型的建立无需依赖过多的专业知识，且故障分类精度提高了约6%。Ince等[15]基于一维卷积神经网络提出一种新的电机状态监测系统，该系统可通过适当的训练提取最优特征，并能够实现高于97%的故障检测精度。Abdeljaber等[16]提出一种基于一维卷积神经网络自适应实现的缺陷检测方法，并通过看台模拟器主钢架的监测试验验证了其方法的有效性。试验结果表明，该方法在实时结构缺陷检测过程中具有较高的性能。Pandey等[17]利用超声导波对铝板的缺陷进行自动检测，通过建立一维卷积神经网络的缺陷分类模型，实现了接近100%的识别准确率。如上所述，已有研究中针对一维信号采用的均为单一尺度的特征提取，并未充分发挥CNN提取一维信号特征的能力，特征提取效果仍有较大提升空间。为此，本文研究并提出了基于改进一维卷积神经网络的管道缺陷识别方法，设计了多尺度特征提取模块，能够有效挖掘故障数据中的特征信息。

2 裂纹缺陷有限元仿真建模

本文基于商业有限元分析软件(COMSOL Multiphysics 5.6)建立三维直管模型，并基于该模型进行仿真试验分析。所建立模型的实物对象为某舰船上长度2.0 m，外径114.0 mm，壁厚7.2 mm的铜合金管，具体材料特性如表1所示。

表1 铜合金管材料特性Tab.1 Properties of copper alloy pipe materials

基于目前的导波检测水平，可以检测运行管道中最低1%横截面积的缺陷[18]。考虑到在管道中一旦产生裂纹，那么随着时间的推移，裂纹将逐渐形成动态的无序扩展[19]。为此，在仿真模型中将最小截面缺损率设置为4%。此外，令不同等级之间的截面缺损率区间值逐步增加，直至裂纹扩展至1/4管道圆周，具体数值设置如表2所示。

表2 裂纹仿真尺寸Tab.2 Crack simulation size

考虑到超声导波的多模态和频散特性，本文选取导波模态为T(0,1)，并调制10个周期的汉宁窗函数作为激励信号。根据图2所示的铜合金管群速度频散曲线，选择40 kHz作为激励信号的频率。此外，选取距离激发端0.1 m等间距的36个外部节点作为反射信号接收端。在仿真建模中，模型的裂纹缺陷设置为缺口状、边缘均匀。网格划分是决定仿真模型计算精度的重要步骤，网格的密度越高，计算精度越准确，但计算所需的时间也会越多。为优化有限元模型的整体网格节点数量，减少计算时间，本文采用分割域的方式将管道裂纹区域与无缺陷区域划分开来。其中，无缺陷区域网格为映射扫掠，具体为管道端面径向2个单元格，圆周方向48个单元格，轴向网格间距设置为2.0 mm，从而确保网格单元尺寸小于模型中最小波长的1/10[20]；有缺陷区域为自由四面体网格加密处理，最小单元0.4 mm。综上所述，本文所建立的有限元仿真模型结构如图3所示。5种裂纹等级的缺陷回波信号如图4所示。

图2 群速度频散曲线Fig.2 Group velocity dispersion curves

图3 缺陷仿真示意图Fig.3 Defect simulation diagram

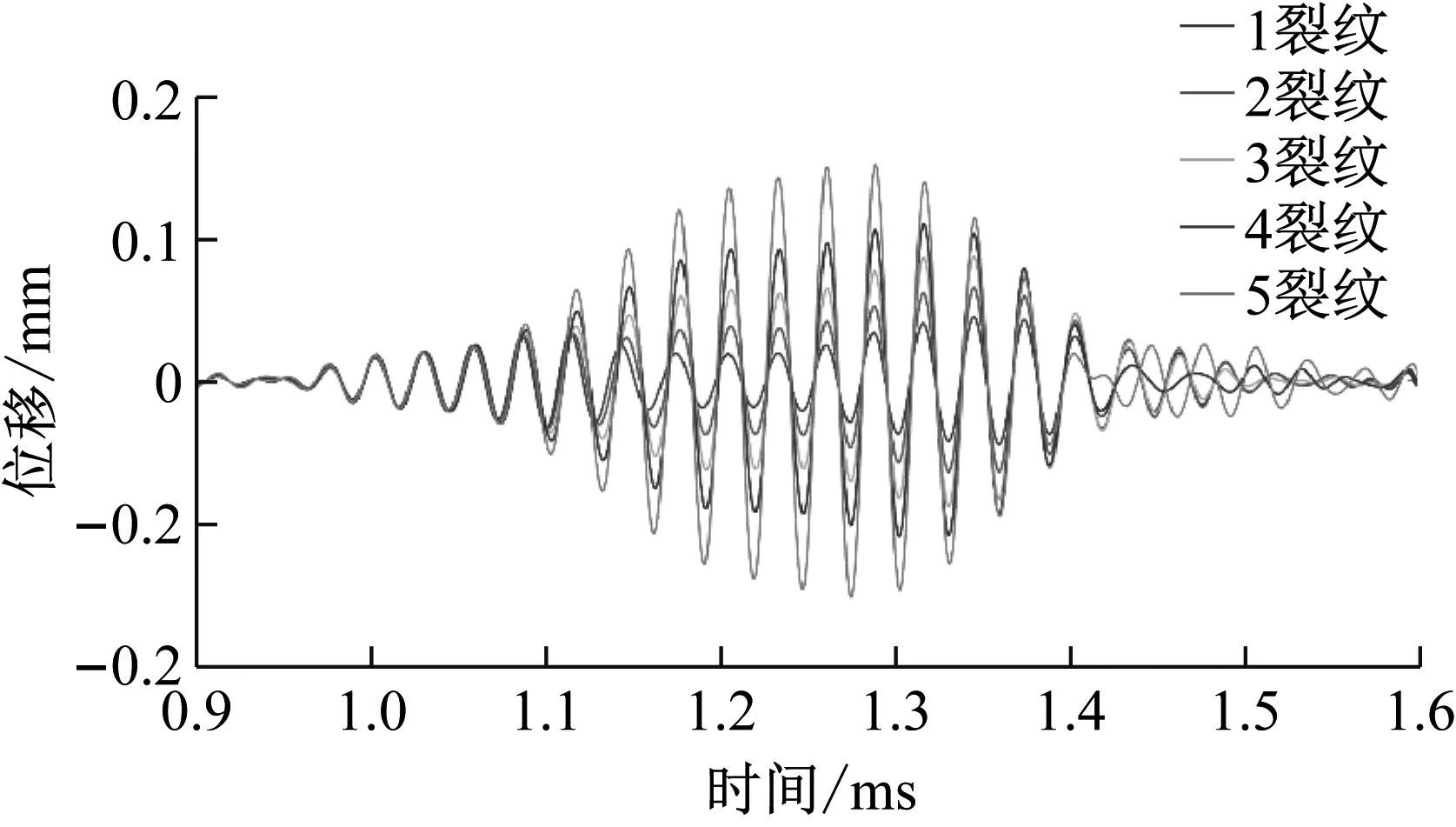
图4 不同裂纹等级的回波信号Fig.4 Echo signals of different crack grades

3 基于1DCNN的裂纹等级分类模型

基于上述设置，通过有限元仿真生成共计1 100个数据样本作为输入，每个数据样本由1 400个标量点组成。在此基础上，将随机880个仿真数据样本用作为训练集，剩余220个仿真数据样本用作为验证集。

3.1 环境配置及模型结构

本文研究所采用的1DCNN基于Tensorflow(2.4.0)版本中的Keras(1.1.2)框架予以实现，试验平台硬件配置为：I7-10875H型CPU，1650型GPU，内存为16 G。为提高分类精度，本文对基础的1DCNN模型结构及相关参数进行了反复的优化试验最终确定1DCNN模型结构为多尺度一维卷积神经网络(MS-1DCNN)，采用并行多分支结构，每个分支包含3个卷积层、3个激活层、3个池化层。此外，上述3个分支对输入分别进行特征提取后再进行特征融合。通过三种不同感受野的卷积核来获取更有效的缺陷信息，大小分别为3、5、7。Strides值设置为1，Padding设置为Same，采用整流线性单元(ReLU)作为每个卷积层的激活函数。此外，为减少网络中的参数量和计算量，在第三个卷积层之后进行池化操作。Maxpooling尺寸设置为2.0，Dropout参数设置为0.2，添加Flatten层将多维数据展平，在全连接层的输出层中使用Softmax作为激活函数。具体模型结构如图5所示。

图5 MS-1DCNN 网络结构Fig.5 MS-1DCNN network structure

基于上述试验设置，经仿真数据训练后的MS-1DCNN模型学习曲线如图6所示。由图6可见，随着迭代次数的增加，训练集和验证集的准确率逐步提高、损失率逐步下降。当迭代次数达到100次左右时，准确率和损失率的曲线变化幅度趋于平缓，且验证集的准确率曲线高于训练集的准确率曲线，验证集的损失率曲线低于训练集的准确率曲线。由此可见，所建立的MS-1DCNN模型拟合情况良好。

图6 MS-1DCNN模型训练学习曲线Fig.6 MS-1DCNN model training learning curve

3.2 对比方法

为验证本文所提出的基于MS-1DCNN的管道裂纹等级识别模型的分类能力，引入5种具有代表性的机器学习分类模型进行对比试验，具体包括：以BP神经网络(back-propagation, BP)为代表的黑盒模型、以支持向量机(SVM)为代表的单分类器模型、以XGBoost为代表的多分类器组合的集成学习模型、以及以1DCNN为代表的深度学习模型。为确保用作为对比试验的各机器学习模型具有较好的识别结果，在多次调参试验后，确定各机器学习模型的参数设置如下：BP神经网络迭代次数为20 000，隐含层数为7；SVM采用二次核函数；XGBoost采用5折交叉验证，子树数量(estimators)设置为100；1DCNN设置为3个卷积层、1个池化层以及1个全连接层，各卷积层均采用16个大小为15的卷积核。

由于试验采用了10个周期、40 kHz的低频导波信号，故其在频域上包含的缺陷信息相对较少，频域特征参数不能准确地区分不同裂纹等级之间的细微变化。此外，考虑到导波检测中激励信号与缺陷反射信号都具有明显的时域特征信息，为此，本文采用时域分析法进行特征提取。具体地，定义如下特征指标以实现对缺陷反射信号的时域特征提取：峰峰值、方差、均方根、标准偏差、平均值、偏度、峰度、离散系数、峰值因子、波形因子、脉冲因子、裕度因子、峰度因子(分别标记为TD1-TD13)。各特征指标的具体定义式如表3所示。

表3 时域特征参数定义Tab.3 Definition of time-domain characteristic parameters

3.3 试验设计及结果分析

考虑到在实际中受试验环境和硬件设备的影响，试验中采集到的数据往往被噪声污染。因此，通过有限元模型生成的仿真数据与试验数据之间势必存在一定差异。为使仿真数据更好地模拟试验中的真实数据，将具有不同等级信噪比(SNR)的高斯白噪声叠加到仿真数据，以生成不同等级的含噪数据样本。具体地，噪声区间设置为[2,20]dB，步长设置为2 dB。在此基础上，将上述共计10个等级的含噪数据与无噪声仿真数据分别放入各模型中进行10次独立重复试验，通过对比各模型的正确识别率，从而检验本文所提出的MS-1DCNN模型在噪声环境下的鲁棒性。各模型在不同噪声等级下的平均正确识别率如图7所示。

图7 各模型基于不同信噪比的含噪数据的识别精度对比Fig.7 Comparison of recognition accuracy of noise-containing data based on different SNRs of each model

由图7可以看出，在无噪声情况下，几乎所有模型都能达到100%的准确率。然而，随着噪声数据中SNR值的逐渐降低，各模型的正确识别率随之下降。当SNR=20 dB时，BP和SVM的正确识别率出现大幅度下降，正确识别率低至50%以下，已然不具备较准确的识别能力；相比之下，MS-1DCNN和1DCNN的正确识别率能够依然保持100%；XGBoost的正确识别率虽略有降低，但能够稳定在90%以上。当12 dB≤SNR<20 dB时，MS-1DCNN和1DCNN的正确识别率相差较小，且始终保持在较高水平。然而，XGBoost的正确识别率下降明显。当2 dB≤SNR<12 dB时，MS-1DCNN的正确识别率最高，显著优于1DCNN、XGBoost、SVM、BP等模型。由上述分析可见，本文所提出的MS-1DCNN模型对噪声具有较强的鲁棒性。

4 实例验证

为进一步验证本文所提方法在实际应用中的有效性，搭建基于磁致伸缩效应的超声导波检测系统对第2节所述含裂纹缺陷的铜合金管进行试验验证。所搭建的具体试验装置如图8所示。在试验过程中，由信号发生器产生10个周期的40 kHz脉冲信号，该信号经由功率放大器放大后被加载到条带传感器上。其中，发射端与接收端的条带传感器均放置在待检管道的同一端。在管道沿圆周方向通过环氧树脂粘贴铁钴条带并用永磁铁磁化，条带传感器在管道中激励出T(0,1)模态导波耦合到管道中沿长度方向传播。当导波信号遇到缺陷时发生反射和透射，接收传感器感应到微弱回波信号后经由前置放大器和高通滤波器处理，并进一步通过数据采集系统采集回上位机端。

图8 试验装置Fig.8 Test installation

考虑到实船退役铜合金管的稀缺性和较高的实际成本，本文在试验中对已获取的单根铜合金管以机械加工的方式制作弧长为80 mm，宽度2 mm，深度3 mm的裂纹缺陷。所制缺陷对应第2章中仿真裂纹模型的第5等级，具体如图9所示。

(a) 仿真模型裂纹

(b) 试验管道裂纹图9 裂纹缺陷示意图Fig.9 Crack defect schematic diagram

基于所搭建的磁致伸缩超声导波检测系统，经多次重复试验获取图9所示裂纹缺陷的样本数据库，并将其用作为MS-1DCNN模型的测试集。采用第3章中建立并训练完备的MS-1DCNN模型对实管测试集样本进行识别，各信噪比下10次独立试验的平均正确识别率如图10所示。

图10 不同信噪比下MS-1DCNN的准确度Fig.10 Accuracy of MS-1DCNN under different SNR

由图10可见，当SNR从2 dB上升至14 dB时，MS-1DCNN对实管缺陷的正确识别率逐渐升高；当SNR=14 dB时，MS-1DCNN的实管缺陷正确识别率达到88.9%；当SNR>14 dB时，MS-1DCNN对实管缺陷的正确识别率开始逐渐下降。由此可见，14 dB的噪声数据与试验数据在MS-1DCNN中提取的特征最为接近。

考虑到试验过程中引入噪声信号的随机性，带有裂纹缺陷的铜合金管在不同时刻、不同工况下所采集到的试验数据并非完全一致。为确保用于模型训练的仿真数据更接近实际数据，本文进一步将包含不同信噪比的噪声数据按区间进行组合并用于模型训练，以求获取鲁棒性更强的MS-1DCNN模型用于实管缺陷的检测识别。具体地，将SNR=1、SNR=2、SNR=3的仿真数据归为一组，将SNR=4、SNR=5、SNR=6的仿真数据归为一组，以此类推共得到7个信噪比区段的数据组并完成对各自MS-1DCNN模型的训练。各信噪比区段对应的MS-1DCNN模型对实管缺陷的正确识别率如图11所示。

图11 不同信噪比组合下MS-1DCNN的准确度Fig.11 Accuracy of MS-1DCNN under different SNR combinations

由图11可见，在测试集不变的情况下，基于噪声数据组合训练的MS-1DCNN具有更高的正确识别率。其中，13～15 dB噪声区段训练的模型对实管缺陷有着最高90.1%的正确识别率，相比于单噪声数据训练的MS-1DCNN模型有所提升。从整体来看，无论MS-1DCNN输入的是单噪声数据还是噪声区段数据，其对实管缺陷的正确识别率均存在峰值点，且正确识别率曲线近似服从正态分布。由此可见，对仿真数据添加噪声的方法在一定程度上可以更好地逼近物理试验数据，基于融合噪声数据训练的MS-1DCNN相比于单纯仿真数据训练的MS-1DCNN而言，对实际物理系统的缺陷数据有更强的识别分类能力，而通过噪声区段组合数据训练得到的MS-1DCNN模型对于实管缺陷的识别结果有着更进一步的提升。

5 结 论

本文提出一种基于多尺度一维卷积神经网络的超声导波管道结构健康监测模型，以实现对管道裂纹不同扩展等级的准确分类。一方面，本文对管道裂纹有限元模型获得的仿真数据进行不同程度的加噪处理，并通过与BP、SVM、XGBoost、1DCNN等模型的对比分析，验证了本文所提出的MS-1DCNN模型在不同噪声等级情况下都能够保持较高的分类精度，具有较强的鲁棒性。另一方面，通过搭建基于铜合金管的物理试验平台并开展超声导波检测试验，实现了有限元仿真数据样本与物理系统试验样本的相互融合，进一步验证了本文方法在工程实际背景下能够有效地检测出管道裂纹缺陷并给出缺陷的量化评级。

本文所提出的基于MS-1DCNN的裂纹等级识别方法可直接处理原始导波信号，无需复杂的人工特征提取过程和过多的专家经验，且对环境噪声具有较强的特征提取能力。在实际工程中可利用有限元仿真和机器学习方法相结合以构建被检管道的缺陷识别模型，通过模拟多类别的结构损伤为管道的结构健康监测提供新的解决方案，具有良好的应用前景。