基于CEEMDAN多尺度排列熵和SO-RELM的高压隔膜泵单向阀故障诊断
李 瑞, 范玉刚
(1.昆明理工大学 信息工程与自动化学院,昆明 650500;2.云南省人工智能重点实验室,昆明 650500)
高压隔膜泵作为一种新型物料输送设备,广泛应用于精细化工、冶金铸造和废水处理等领域[1]。单向阀作为高压隔膜泵组件中的关键设备,是最易发生故障的部件之一,其工作状态直接影响高压隔膜泵能否正常运行[2-3]。因此,针对高压隔膜泵单向阀进行故障诊断研究具有重要意义。
单向阀振动信号中蕴含着运行状态信息,对振动信号进行特征提取,是单向阀故障检测的关键。高压隔膜泵结构复杂,运行工况多样。例如,高压隔膜泵的压力和转速随负荷变化而波动,矿浆粒径、浓度和流速随物料变换而变化,这些因素共同作用下,导致单向阀振动信号具有非线性、非平稳特点。经验模态分解(empirical mode decomposition, EMD)[4]方法对于非线性、非平稳信号的分析效果较好,但EMD方法分解的IMFs存在模态混叠现象。集合经验模态分解(ensemble empirical mode decomposition,EEMD)[5]方通过在待分析信号中加入相互独立的白噪声,解决EMD方法的模态混叠问题,但是由于加入白噪声,计算量增加,分解过程中仍会存在残余的白噪声[6]。互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)[7]方法在原始信号中加入互为相反数的正负白噪声,解决了EEMD方法分解后信号中有残余白噪声的问题,同时减少分解时迭代次数,降低计算量。自适应噪声完备经验模态分解(complementary ensemble empirical mode decomposition with adaptive noise, CEEMDAN)[8]方法对CEEMD方法进行了改进,通过自适应加入白噪声,消除虚假的IMF分量,重构误差几乎为0,完备性较好[9]。
单向阀振动信号经CEEMDAN方法分解得到的IMFs内含丰富的单向阀故障特征信息,通过熵理论对IMFs特征信息进行精确表征。排列熵(permutation entropy, PE)[10]算法能够准确、快速找到振动信号的突变信息进行放大,其抗干扰性强[11]。但由于高压隔膜泵单向阀振动信号的非平稳、时变特性,其故障特征信息内含于多尺度时间序列中,单一尺度排列熵提取信息有限。多尺度排列熵(MPE)[12]针对复杂振动信号依照时间序列进行多尺度特征提取,全面表征振动信号内部信息。谭鸿创等[13]提出将MPE与LPP相结合的方法对螺旋锥齿轮振动信号进行特征提取,并建立基于ELM (extreme learning machine)的故障诊断模型。董治麟等[14]通过MPE表征滚动轴承振动信号的故障特征,并输入ELM模型进行故障诊断,提升滚动轴承故障识别精度。因此,ELM是建立故障诊断模型的有效方法。然而,ELM在训练过程中存在输出层权值矩阵较大等问题[15-16],不利于建立稳定的识别模型。正则化极限学习机(regularized extreme learning machine,RELM)[17]通过引入正则项对输出权值范围进行控制,可有效克服ELM模型过拟合问题,提升模型的泛化性能。但是RELM模型同ELM一样,输入层权值和隐含层偏置都是随机给定的[18],影响RELM模型的稳定性和分类精度。为此,本文提出结构优化正则化极限学习机(SO-RELM)算法,利用K-means算法[19]和轮廓系数法[20]优化RELM结构,提高模型识别精确度及稳定性。
本文针对高压隔膜泵单向阀振动信号非平稳、非线性的特点,提取CEEMDAN分量的多尺度排列熵特征,用于表征单向阀运行状态的非线性动力学特征。并基于多尺度排列熵,提出了结构优化正则化极限学习机故障诊断模型,提高RELM模型识别精确度及稳定性。
1 信号特征提取
1.1 自适应噪声完备经验模态分解
CEEMDAN通过向振动信号加入有限次的自适应高斯白噪声来辅助分解,以减小重构误差和提高分解效率,可以有效解决EMD中的模态混叠缺陷以及EEMD中计算复杂度高和虚假IMFs多的问题。CEEMDAN信号分解步骤如下:
(1) 对原始振动信号x(n)添加高斯白噪声ωi(n)得到xi(n)=x(n)+γ0ωi(n),其中,γ0为噪声标准差。利用EMD对xi(n)进行N次分解得到CEEMDAN的IMF1为
(1)
(2) 计算第1阶段的残余序列r1(n)。
r1(n)=x(n)-IMF1(n)
(2)
(3) 对r1(n)+γ1IMF1(ωi(n))进行EMD信号分解得到CEEMDAN第2阶段的IMF2为
(3)
(4) 以此类推计算至k+1阶段,得到第k阶段的残余序列rk(n)和第k+1个模态分量IMFk+1。
rk(n)=rk-1(n)-IMFk(n)
(4)
(5)
(5) 重复执行步骤(4)直到残余序列的极值点个数≤2,则停止进行EMD信号分解。CEEMDAN最终得到残余序列R(n)和固有模态分量IMFK,原始振动信号x(n)可表示为
(6)
1.2 相关系数法
CEEMDAN对单向阀振动信号进行分解得到的若干IMFs中,部分IMFs含有原始振动信号的故障信息,剩余IMFs则是因为分解时迭代误差、现场噪声影响产生的干扰分量。为了有效提取振动信号的故障信息,需要剔除故障无关和干扰IMFs,来提高故障识别的准确率。本文利用相关系数法选择有效IMFs。
相关系数反映出IMFs与原始振动信号的相关程度。包含主要故障信息的IMFs与原始振动信号具有较高的相关性,虚假IMFs的相关性较低。原始振动信号x(t)与其经CEEMDAN分解后的IMFs,h1(t),h2(t),…,hn(t)的相关系数ρi计算公式为
(7)
设置门限阈值Th为相关系数的标准差,即
(8)
如果ρi>Th则保留第i个IMF,否则剔除第i个IMF。
本文计算IMFs的相关系数并选取相关系数大于阈值的IMFs作为敏感IMFs。
1.3 多尺度排列熵
排列熵能够表征复杂时间序列振动信号的随机性,精准捕捉数据的动态变化,但其只能反映单一尺度下信号的突变信息。多尺度排列熵(MPE)通过将时间序列振动信号进行多尺度粗粒并计算其排列熵值。多尺度排列熵算法原理如下:
给定一个时间序列长度为N的机械振动信号X={xi,i=1,2,…,N},粗粒化处理后序列为
(9)
式中:s为尺度因子;[N/s]为N/s取整。

(10)
式中:m为嵌入维数;τ为延迟时间;l为第l个重构分量,l=1,2,…,N-(m-1)τ。对重构分量中的元素进行升序排列,并取元素位置的列索引组成的一组位置序列为
S(r)=(l1,l2,…,lm)
(11)
式中,r=1,2,…,R,且R≤m!。位置序列存在m!种排列的可能性,计算每一种位置序列在Y中出现的可能性{P1,P2,…,Pr}。时间序列振动信号的排列熵公式为
(12)

(13)
本章节对高压隔膜泵单向阀振动信号进行CEEMDAN分解得到若干IMFs,以相关系数方法为度量指标对IMFs进行筛选,计算优选出的IMFs多尺度排列熵,提取单向阀非线性动力学特征,为下一步故障诊断做准备。
2 结构优化正则化极限学习机
RELM虽降低了ELM模型中过拟合现象,但RELM与ELM中输入层与隐含层之间的权值以及隐含层节点的阈值都是随机给定的,这些参数并不是最优组合,会影响RELM模型的稳定性和故障诊断精度。对此,本文采用K-means聚类算法和轮廓系数法优化RELM结构中神经元个数、激活函数数据中心和拓展宽度。从而达到优化RELM的网络结构,提高模型识别精度的目的。
2.1 正则化极限学习机
为了提高ELM模型的泛化能力,RELM通过引入正则项,控制权值矩阵β的范数值,获得最小训练误差和输出权重。RELM所要求解的目标函数为
(14)

通过目标函数构建Lagrange方程
αT(Hβ-T-ε)
(15)
式中,αi∈R(i=1,2,3,…,N)为拉格朗日算子。分别对式(15)中变量求偏导并令各式等于零,可得

(16)
对式(16)用最小二乘法计算,得到输出权值矩阵
(17)
综上,对于给定SO-RELM神经网络的一个输入x,预测输出y可表示为
(18)
2.2 K-means确定SO-RELM隐含层节点的数据中心Cj和拓展宽度δj
K-means聚类算法按照数据样本之间的相似性进行聚类划分,通过距离函数计算样本相似度,并把相似度高的样本划分至同一簇类。K-means聚类算法流程如下:
(1) 对于训练样本集D={x1,x2,…,xm},设定k个聚类空集簇P={P1,P2,…,Pk}和最大迭代次数N。
(2) 在训练样本集D内任意选择k个数据样本为质心向量:{C1,C2,…,Ck}。
(3) 计算数据样本xi(i=1,2,…,m)与质心向量Cj(j=1,2,…,k)的欧氏距离
dij=xi-Cj2
(19)
把xi标记为dij最小的Cj所对应的类别λj,并更新Pλj=Pλj∪{xi}。
(4) 对任意簇Pj(j=1,2,…,k)中全部样本点重新计算质心
(20)
(5) 重复步骤(3)和(4),直至所有质心C位置均不变或达到最大迭代次数N。
2.3 轮廓系数法确定SO-RELM隐含层神经元个数
K-means聚类算法中质心数目k值对聚类效果有较大影响,k值还决定着RELM中隐含层神经元个数。在实际应用中,质心数目k值是凭借经验获得的,需要投入大量的精力和时间对模型进行训练。因此,为了更加快速高效地确定SO-RELM隐含层神经元的个数,本文利用轮廓系数法确定质心数目k。
轮廓系数法通过计算簇内的聚合度和簇间的分离度来评估聚类的效果,确定最佳质心数目k。簇内聚合度是衡量同一簇内样本差别的参数。对于样本集D={x1,x2,…,xm},轮廓系数法中聚合度计算公式为
(21)
聚合度a为数据样本xi到同一簇类其他全部样本的平均距离。轮廓系数法中分离度计算公式为
(22)
分离度b为簇内数据样本xi到距离最近簇所含全部样本的平均距离。则簇内数据样本xi的轮廓系数可以表示为
(23)

(24)

轮廓系数法和K-means聚类算法确定的k值作为RELM隐含层节点神经元的个数、将确定的聚类中心Cj作为隐含层节点的数据中心、将聚类半径ri作为各神经元第j个隐含层节点的拓展宽度δj。
3 基于CEEMDAN分量排列熵和SO-RELM的高压隔膜泵单向阀故障诊断
单向阀在高压隔膜泵中需要保持频繁的周期性运动,故障信号呈非线性非平稳特性,通过CEEMDAN算法分解得到IMFs的多尺度排列熵值作为故障特征,以SO-RELM模型对单向阀进行故障识别。基于CEEMDAN多尺度排列熵和SO-RELM的高压隔膜泵单向阀故障诊断方法步骤如下:
(1) 使用加速度传感器采集高压隔膜泵单向阀正常、卡阀、磨损三种状态下的振动信号。
(2) 利用CEEMDAN信号分解方法将单向阀振动信号分解为一系列IMFs。
(3) 计算IMFs与原始振动信号之间的相关系数,并以每种状态IMFs的标准差作为阈值对该状态IMFs进行筛选。
(4) 计算优选出的IMFs的多尺度排列熵并采用KPCA对其降维,组成新的故障特征样本集。
(5) 将步骤(4)得到的故障特征样本集划分为训练样本和测试样本。
(6) 对训练样本进行K-means聚类,得到k个聚类中心,将其设置为RELM模型中数据中心Cj(j=1,2,…,k)。
(7) 计算各簇所有样本点xi到所有聚类中心Cj的欧式距离dl,欧式距离的最大值即为此类样本的聚类半径ri,并将确定的各簇的聚类半径ri作为RELM隐含层节点的拓展宽度δj。
(8) 由轮廓系数法得到质心数目k即为RELM中隐含层神经元的个数。
(9) 最后由轮廓系数法和K-means聚类算法确定最佳质心数目k、聚类中心Cj和聚类半径ri,即为RELM中隐含层神经元的个数、数据中心和拓展宽度。
(10) 求解SO-RELM中隐含层神经元与输出层之间的权值矩阵β。
(11) 将训练得到的参数作为测试样本的输入参数,再把测试样本输入SO-RELM模型,进行故障状态识别,完成单向阀故障诊断。
基于CEEMDAN排列熵-SO-RELM模型的单向阀故障诊断方法流程图如图1所示。
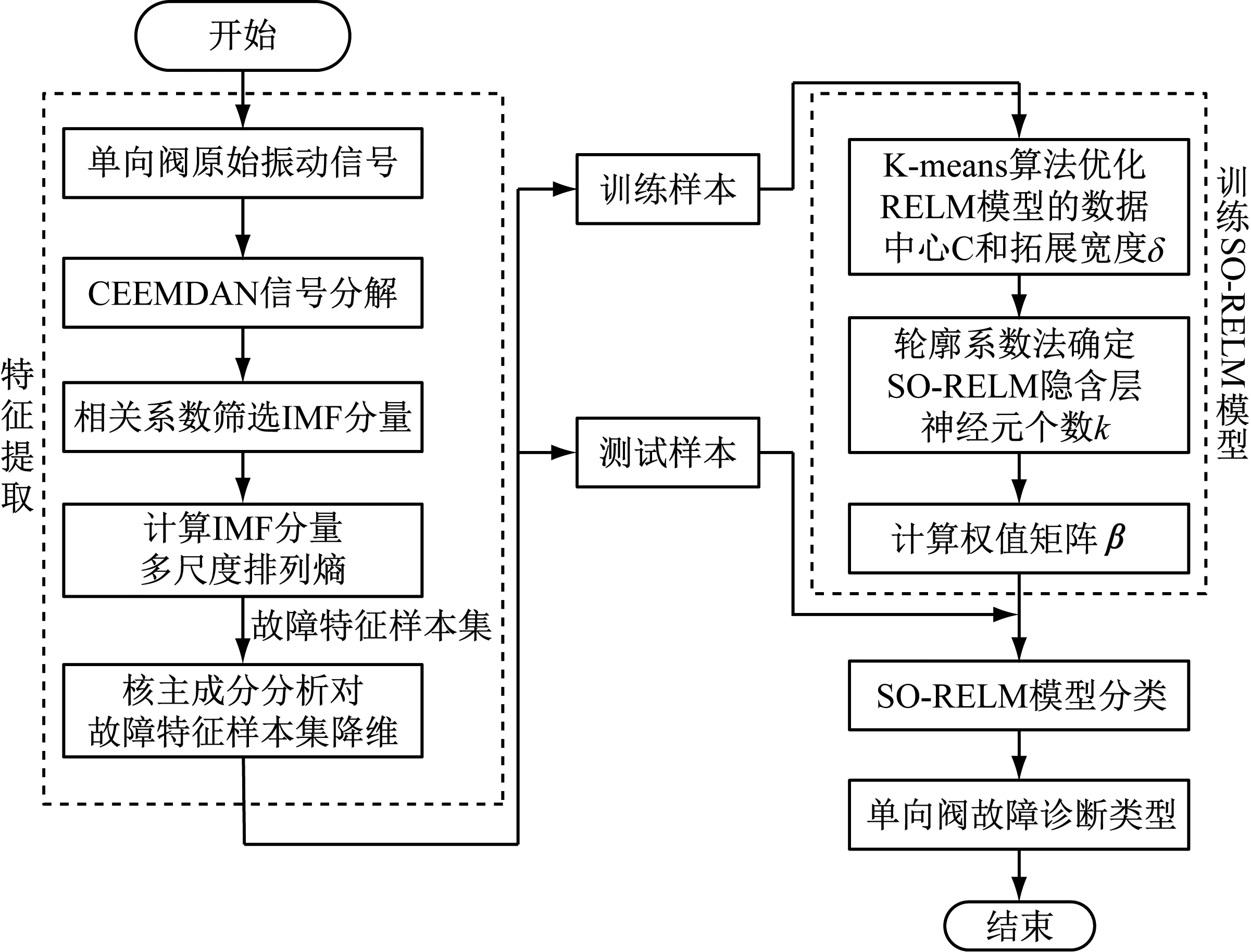
图1 单向阀故障诊断流程图Fig.1 Flow chart of check valve fault
4 试验与分析
4.1 试验设备和数据
本文以云南某铁精矿管道三号高压隔膜泵站单向阀为研究对象,选取单向阀正常、磨损(高硬度砂粒对单向阀反复冲刷导致阀门密封面凹凸不平及存在划痕)和卡阀(粗颗粒卡住单向阀导致阀门关闭不严)状态进行分析,完成对单向阀的故障诊断。采集高压隔膜泵单向阀数据的设备名称和型号如表1所示。

表1 设备名称和型号Tab.1 Equipment name and model
高压隔膜泵单向阀都是进、出口阀成对匹配运行,取三缸曲轴驱动活塞式隔膜泵某一组进、出口阀振动信号进行分析。试验过程中,设定单向阀加速度传感器的采样频率f=2 560 Hz,采集单向阀3种状态在30 s中相同物料流量下的振动信号,每种状态有76 800个采样点。单向阀3种状态时域信号如图2所示。

(a)
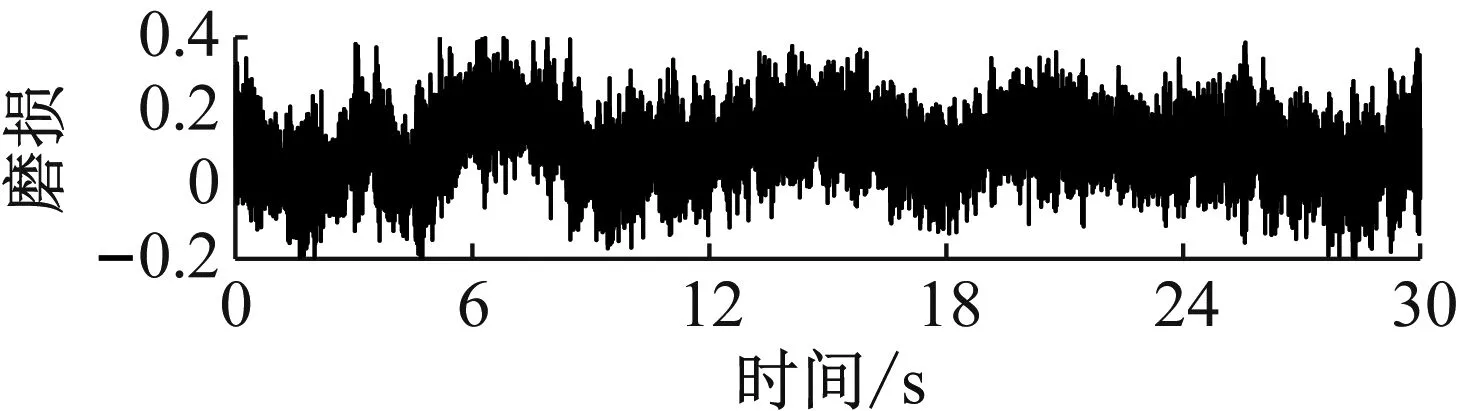
(b)
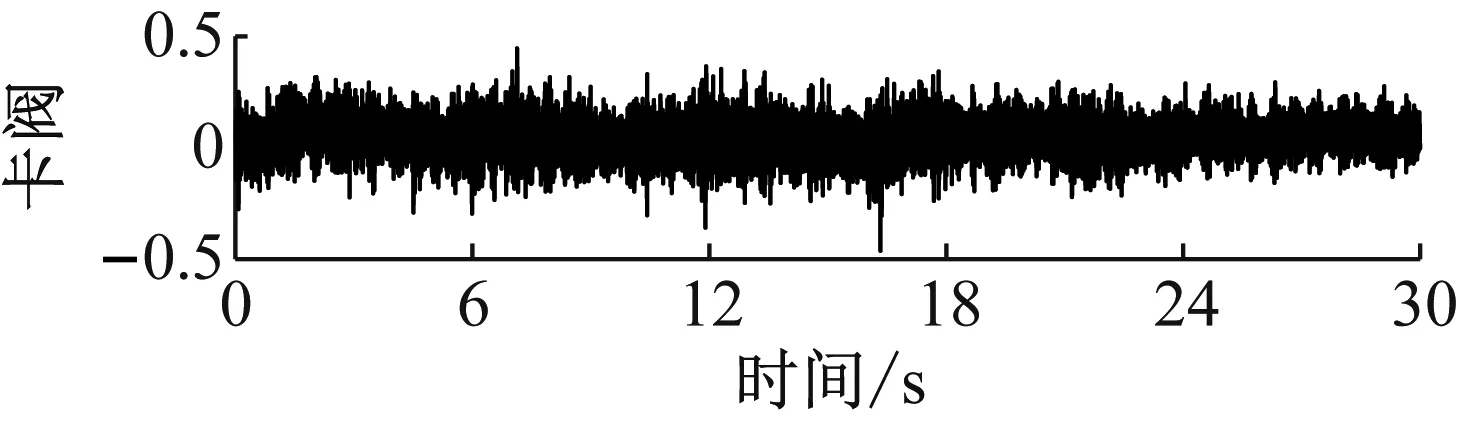
(c)图2 3种状态时域信号Fig.2 Three state time domain signals
4.2 特征提取
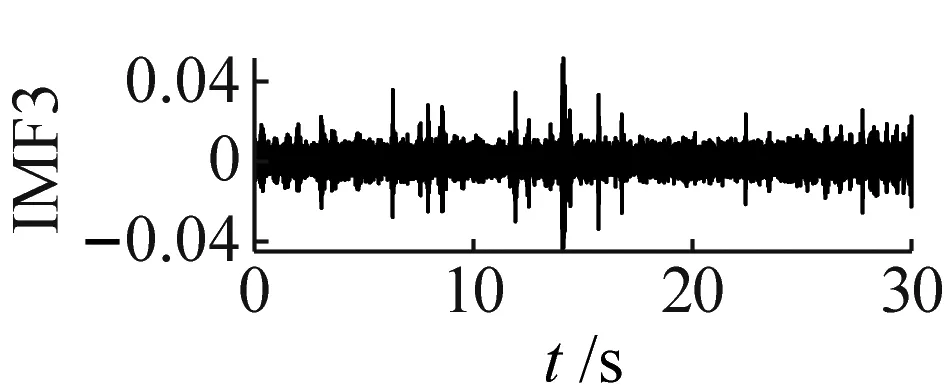
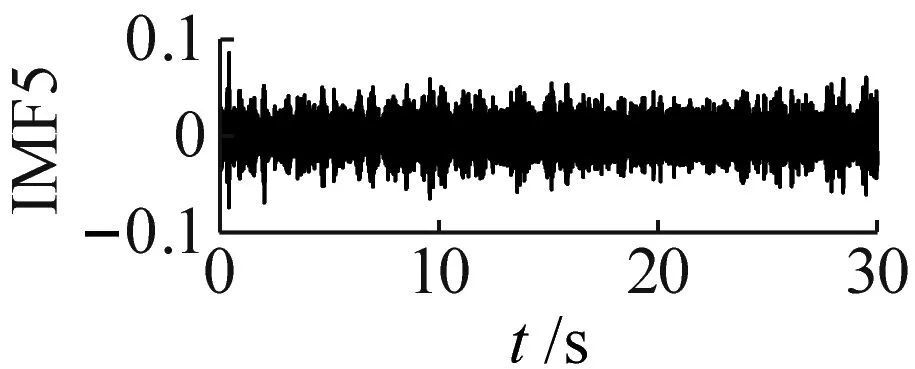
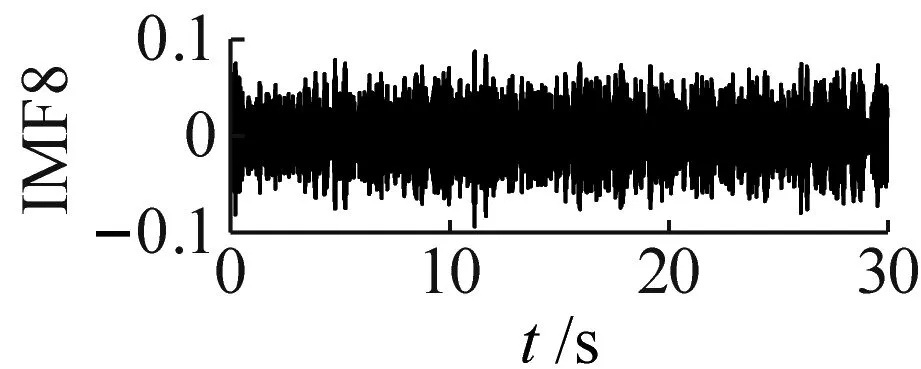
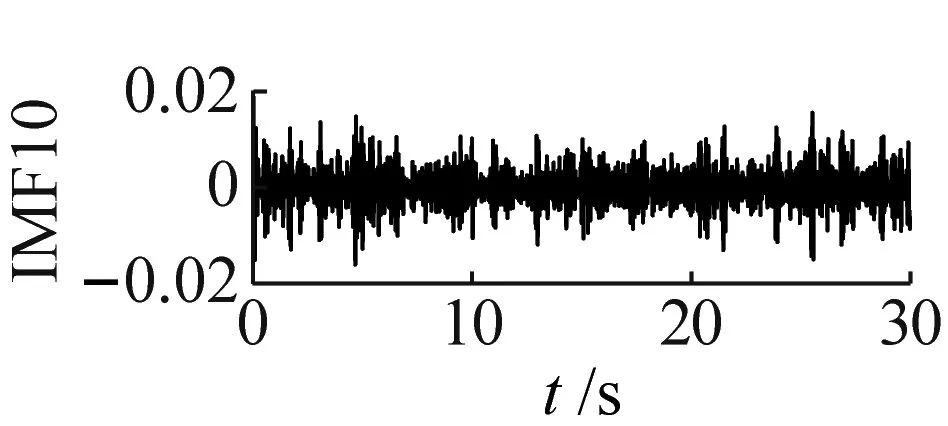
单向阀在高压隔膜泵内需维持频繁周期性运行,其故障信号呈非线性非平稳特性,对单向阀正常、磨损和卡阀状态的振动信号进行CEEMDAN信号分解。其中,噪声标准差为0.2,总体平均次数为100。因篇幅限制,本文仅展示单向阀磨损状态的CEEMDAN结果,如图3所示。由图3可知,单向阀磨损状态振动信号分解为19个IMFs,其中,最后一个IMF为残余分量,各IMF无模态混叠现象。
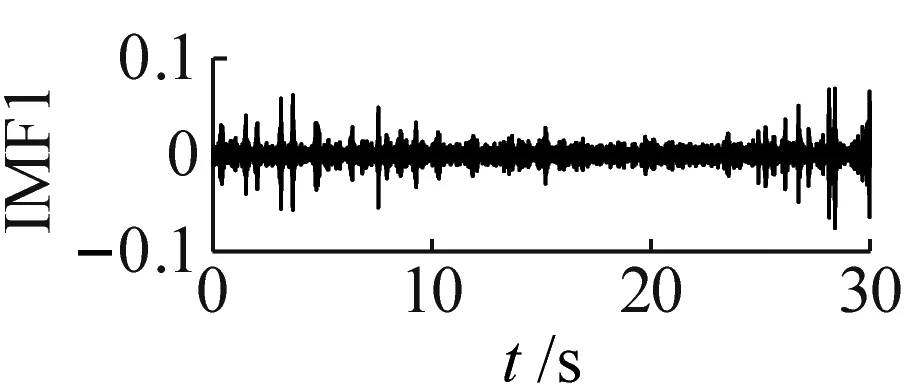
(a)

(b)
(c)

(d)
(e)

(f)

(g)
(h)

(i)
(j)

(k)
(l)

(m)

(n)

(o)

(p)

(q)
(r)

(s)图3 单向阀磨损状态CEEMDAN分解图Fig.3 CEEMDAN exploded view of wear state of check valve
单向阀正常、磨损和卡阀状态振动信号经CEEMDAN信号分解后均得到19个IMFs。为了有效提取振动信号的故障信息,通过相关系数法剔除故障无关和干扰分量,来提高故障识别的准确率。单向阀三种状态下相关系数如表2所示。从表2可知,正常、磨损和卡阀状态的相关系数阈值为0.169 2、0.199 1和0.213 8。正常和卡阀状态的前8阶IMFs,磨损状态的IMF4~IMF8以及IMF14~IMF16与原始振动信号相关程度较高,故选择以上所述IMFs进行试验分析。

表2 3种状态IMFs的相关系数Tab.2 Correlation coefficients of IMFs in three states
基于相关系数法优选出单向阀三种状态的IMFs,计算其多尺度排列熵值组成新的特征向量。多尺度排列熵中嵌入维数m、延迟因子τ和尺度因子s参数值的选择对熵值的计算结果有很大的影响。由文献[21]可知,嵌入维数m取值控制在3~7,m取值较大时,则会增加计算时间,m取值较小时,对信号的突变性检测能力降低。
在不同时延因子τ下排列熵值的变化如图4所示。τ的取值为1~10时,排列熵值范围没有明显变化,表明时延因子τ对排列熵值无明显影响。尺度因子s值设定大于10,单向阀三种状态随尺度因子s增大时多尺度排列熵变化如图5所示。当尺度因子s为 1~8时,正常与卡阀状态的排列熵值差异较小,难以区分两者状态。当尺度因子s大于8时,随着尺度因子s的逐渐增大,正常状态与卡阀状态的排列熵值差异逐渐明显。故本文将嵌入维数m设置为5,延迟因子τ为1,尺度因子s为12。
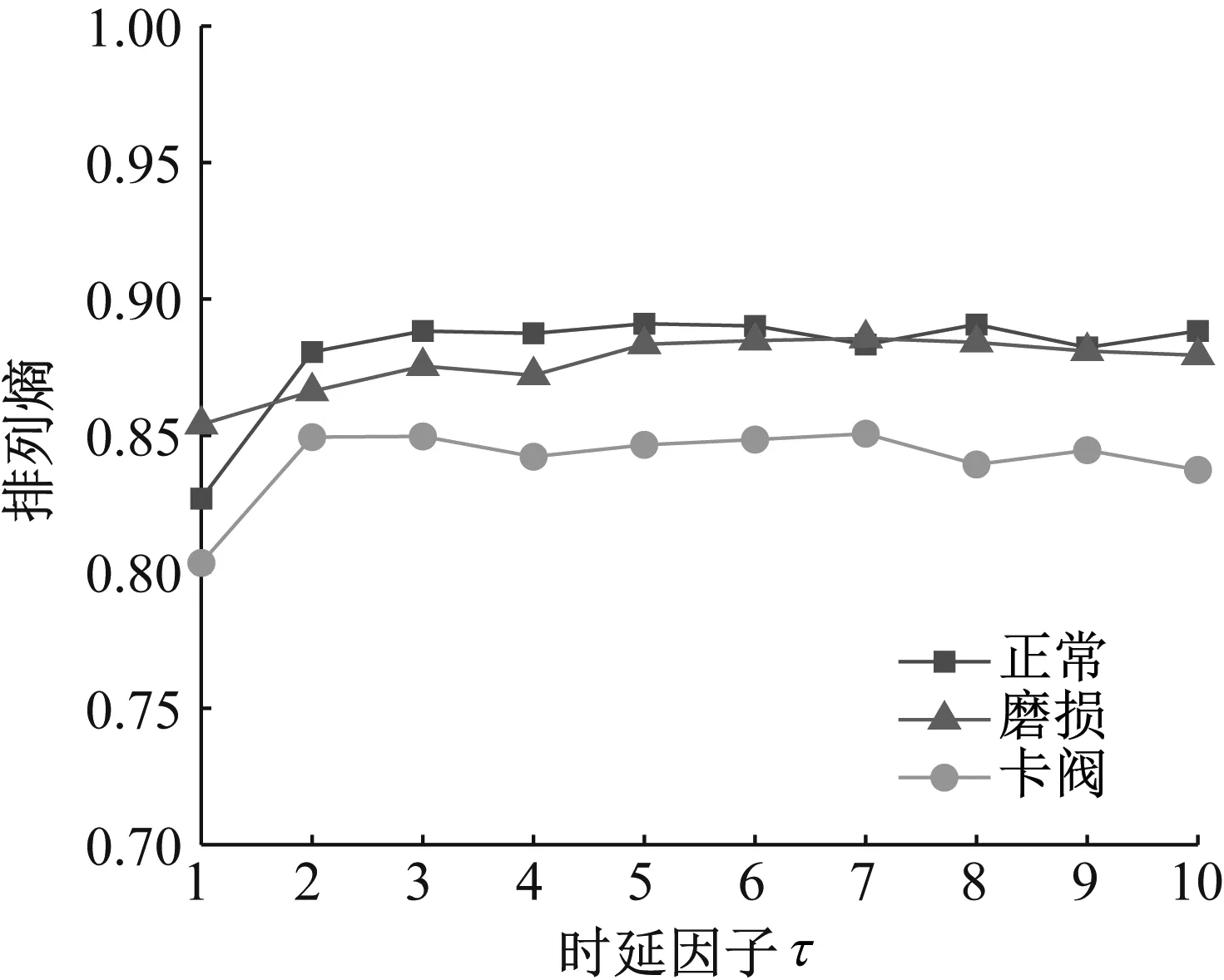
图4 振动信号在不同时延因子下的排列熵Fig.4 Permutation entropy of vibration signals under different time delay factors
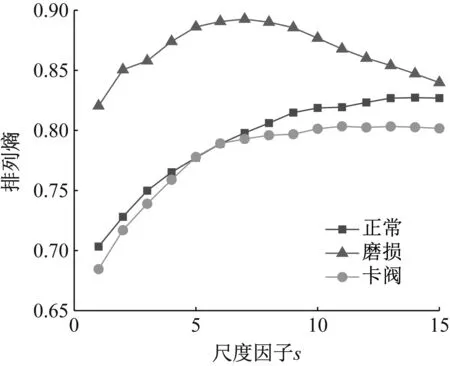
图5 尺度因子对排列熵的影响Fig.5 Influence of scale factor on permutation entropy
计算单向阀3种状态CEEMDAN中筛选出的8个IMFs的多尺度排列熵,并求12个尺度排列熵的均值。单个样本信号长度为N=1 280,故单向阀正常、磨损和卡阀状态均可得到其相对应的60组的故障特征样本。通过核主成分分析法[22]对8维故障特征样本集降维,进行二次特征提取。计算特征的累计贡献率并设定提取效率为85%,故选择主成分特征个数为3,累计贡献率达到87.23%,核主成分分析结果图如图6所示。

图6 核主成分分析结果图Fig.6 Results of nuclear principal component analysis
4.3 故障诊断
单向阀振动信号经CEEMDAN多尺度排列熵特征提取后,每种状态得到60个样本,3种状态共得180个样本。在各个状态的故障特征样本集中随机选择30个样本为训练样本,其余30个样本为测试样本。对训练样本作K-means聚类分析,并绘制质心数目k与轮廓系数的关系曲线,如图7所示。从图7可以看出,当K-means聚类质心数目k为3时,对应训练样本的轮廓系数最大为0.819 5。
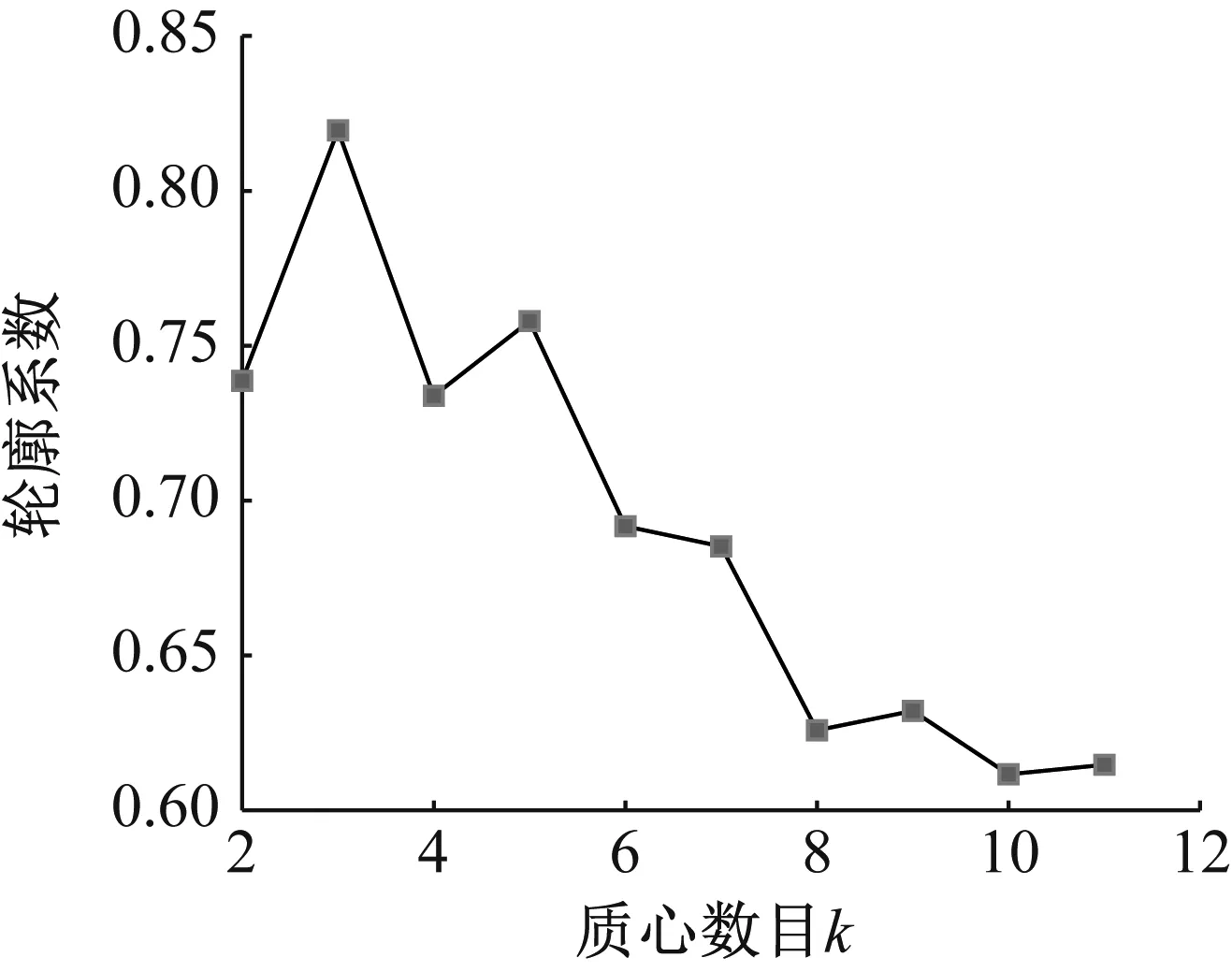
图7 轮廓系数与质心数目k关系曲线Fig.7 Relation curve between contour coefficient and centroid number k
进一步绘制训练样本的K-means聚类结果,如图8所示。由图8可以看出,单向阀3种状态振动信号的CEEMDAN多尺度排列熵特征聚类性强,3类状态间界限分明,特征样本之间无交叉混叠现象。正常、卡阀状态特征分布集中,磨损状态特征分布较为分散。正常、磨损以及卡阀状态的数据中心C分别为(4.033,-3.073 6,0.020 9)、(-8.112 7,0.016 7,-0.053 9)和(4.079 8,3.056 9,0.033 0),拓展宽度δ分别为3.846、35.598和1.211。
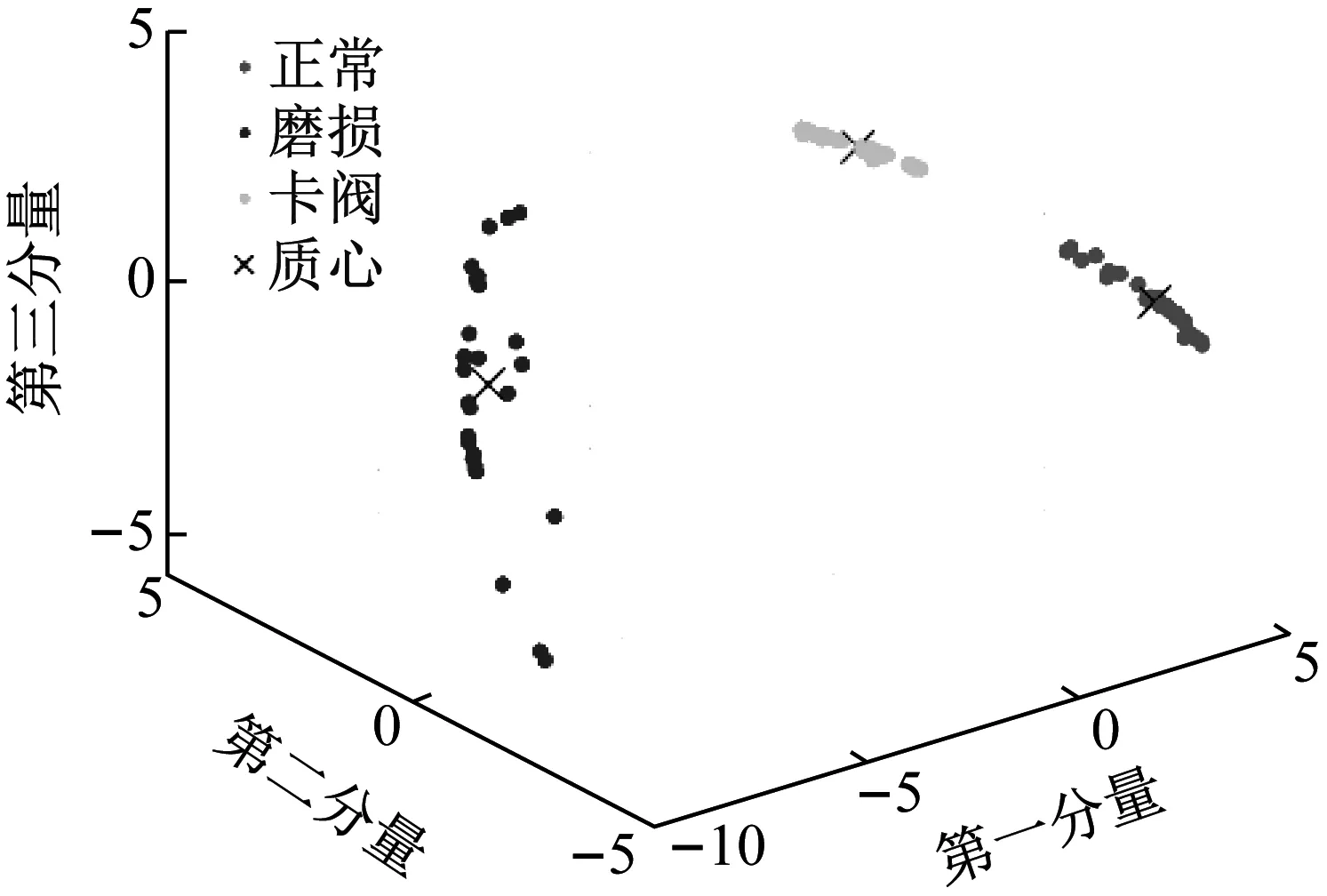
图8 训练样本K-means聚类结果图Fig.8 K-means clustering results of training samples
将训练样本送入SO-RELM模型中训练,得到最佳参数隐含层神经元的数目k、数据中心C和拓展宽度δ,从而建立单向阀故障诊断模型,利用测试样本对模型进行验证,其诊断结果如图9所示。正常、磨损和卡阀状态的标签分别为“1”、“2”和“3”。正常和卡阀状态特征识别率均为100%,磨损状态特征识别率为96.67%,有一个被识别为卡阀状态特征,其原因可能是由于磨损状态特征分散,其测试样本中存在一个明显离群点导致。SO-RELM模型单向阀故障诊断整体识别率为98.89%。

图9 SO-RELM单向阀故障诊断结果图Fig.9 Fault diagnosis results of SO-RELM check valve
4.4 对比试验
为了说明CEEMDAN进行信号分解的优势,图10为EEMD在三种状态下的故障诊断结果。由图10可以看出,单向阀正常状态和卡阀状态易相互诊断错误。其原因为物料运输中含有硬度较大的粗颗粒,在经过单向阀时被卡在阀与阀座之间,但在较短时间内被卡在单向阀中的粗颗粒顺利流出单向阀,会使单向阀正常状态和卡阀故障时的振动信号类似。
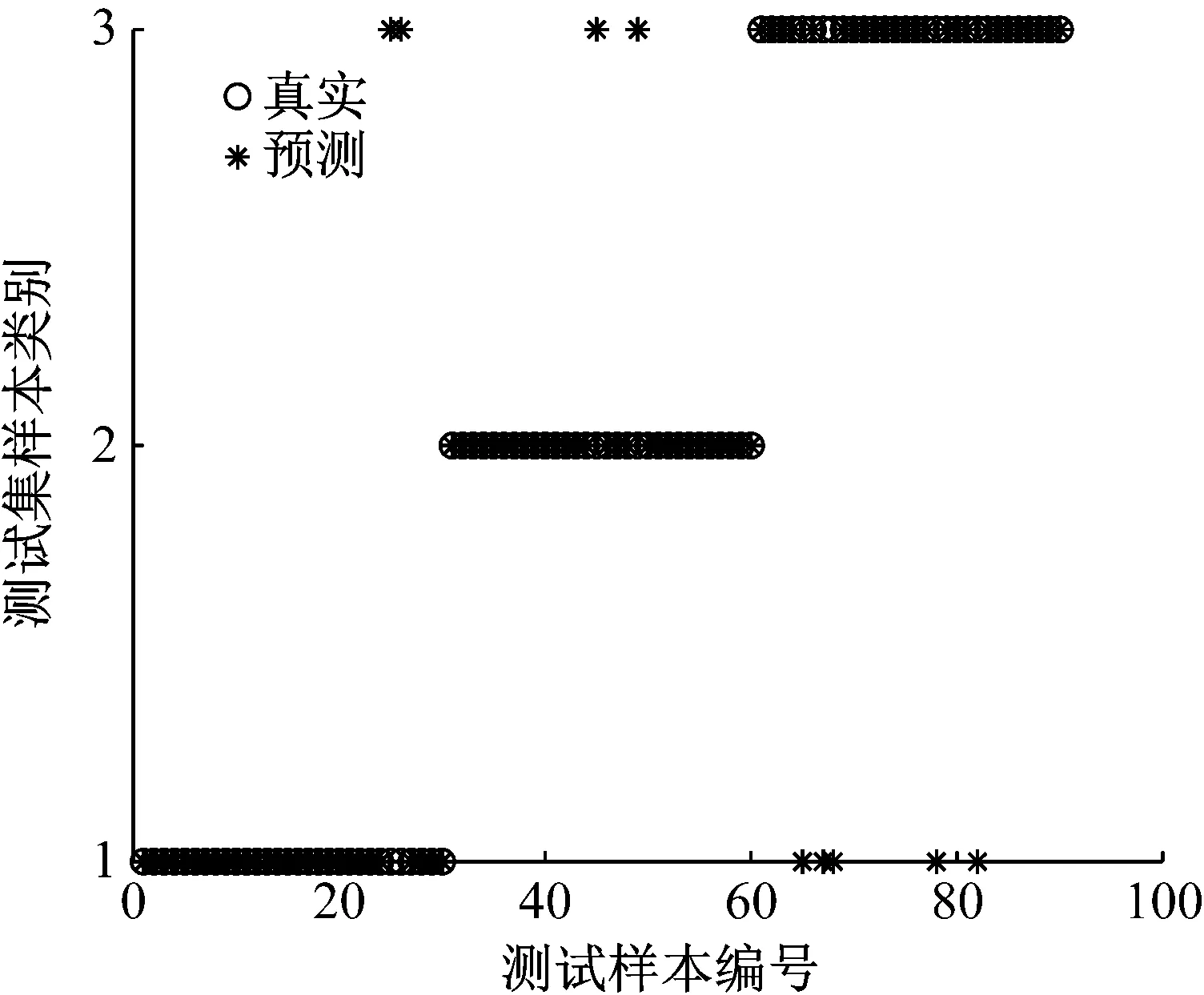
图10 EEMD单向阀故障诊断结果图Fig.10 Fault diagnosis results of so-relm check valve EEMD check valve fault diagnosis result diagram
为验证所提单向阀故障诊断模型的性能,将SO-RELM与BPNN、SVM、ELM和RELM进行单向阀故障诊断的对比试验。四种对比模型的参数设定如下:BPNN结构为3-10-3,激活函数为tansig,学习算法为BPTT,学习率为0.001,训练次数为100次;SVM中RBF参数σ=8.075 8,惩罚因子c=402.4;ELM与RELM隐含层神经元个数为3,激活函数为softplus。基于相同的单向阀振动信号数据和CEEMDAN多尺度排列熵特征提取方法的不同模型对比结果如表3所示。
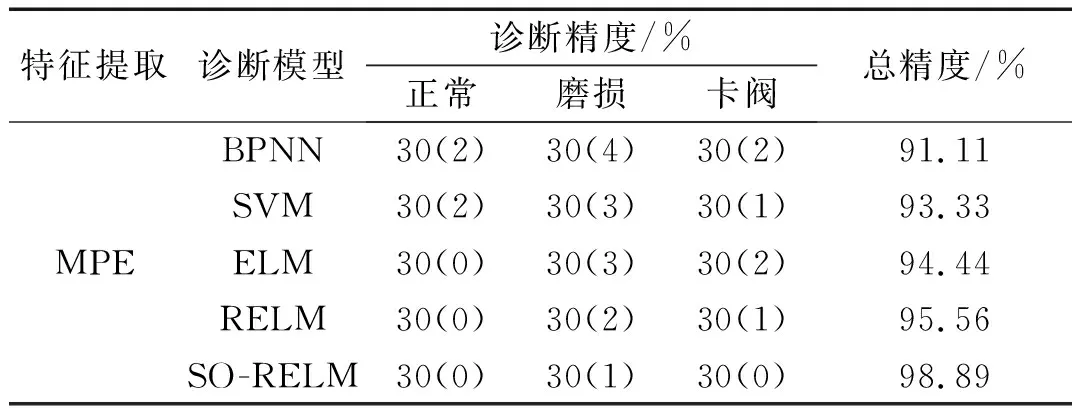
表3 单向阀故障诊断方法对比结果Tab.3 Comparison results of fault diagnosis methods of check valve
从表3可知,本文所提出的故障诊断模型对单向阀识别精度显著高于BPNN、SVM、ELM和RELM方法,SVM、ELM和RELM模型故障识别能力较为接近,SO-RELM模型表现出了最高的诊断精度。因此,本文提出的基于CEEMDAN多尺度排列熵和SO-RELM模型的故障诊断方法可以完成对高压隔膜泵单向阀的故障诊断。
为分析训练样本的大小对本文所提SO-RELM模型故障诊断结果的影响,从单向阀样本特征集中随机选取45、60、75、90、105、120个样本作为训练样本,其余样本为测试样本,其中选取训练样本和测试样本时,每种状态的样本个数相同。单向阀不同分类模型在不同训练样本下的故障诊断结果对比图如图11所示。随着训练样本数的不断增加,SO-RELM模型的故障诊断精度迅速提高,其故障诊断性能明显高于BPNN、SVM、ELM和RELM模型。

图11 不同训练样本集下的故障诊断识别精度Fig.11 Fault diagnosis and recognition accuracy under different training sample sets
5 结 论
为了监测高压隔膜泵单向阀的运行状态,本文针对高压隔膜泵单向阀故障诊断问题,提出一种CEEMDAN分量多尺度排列熵表征设备运行状态的信号特征提取方法,并构建基于SO-RELM的高压隔膜泵单向阀故障诊断模型,试验结果表明:
(1) CEEMDAN多尺度排列熵能够反映高压隔膜泵单向阀振动信号的随机性,精准捕捉振动信号的变化,能够有效提取高压隔膜泵单向阀非线性动力学特征。
(2) 本文采用K-means算法优化了RELM结构,建立的SO-RELM的模型,增强了模型的泛化性能,避免了RELM模型中的不确定性。与BPNN、SVM、ELM和RELM模型相比,SO-RELM模型单向阀故障诊断精度最高达到98.89%。证明了本文所提方法对高压隔膜单向阀故障诊断的有效性。

