基于容积卡尔曼滤波-自适应PID 的共轴无人机设计
赵泽锴,陈 增,古依伶,王玲杜玉,彭晓波,冯文博,张明明
(湖南工业大学 电气与信卢工程学院,湖南 株洲 412007)
近年来我国无人机相关产业不断扩大,无人机从军事领域的专业设备,逐渐普及成为工业领域的巡线无人机、测绘领域的测绘无人机,再到农业领域的植保无人机,最终走进普通消费者生活,用于娱乐、拍摄用途。目前,民用无人机多为多轴气动布局,少数为多轴共轴反桨,其续航能力、自稳定性能瓶颈凸显,无人机长续航设计和强抗风设计矛盾难以调和。该现状在电池与无刷电机性能没有得到突破的情况下难以有质的改变[1-2]。针对以上问题,拟设计一款基于容积卡尔曼滤波-自适应PID 的共轴无人机,该无人机使用与普通多旋翼不同的共轴双旋翼气动布局。与多旋翼相比,共轴双旋翼在有相同的旋翼总面积时单旋翼桨叶尺寸更大,力效更高;在单旋翼面积相同时旋翼总面积更小,抗风性能更好。利用这一设计,能得到更长的续航时间与更理想的悬停稳定性。
1 共轴无人机姿态控制方案
姿态控制系统的机械结构决定了飞行器以何种升力结构、驱动方式获得6 个自由度的姿态调整能力[3]。姿态控制系统采用倾斜旋翼轴方案,整体设计示意图如图1 所示。倾斜旋翼轴方案曾用于早期载人直升机,近年来开始被少量使用在消费级直升机航模上。倾斜旋翼轴方案完全舍弃了一般直升机机械方案中的自动倾斜器总成,转而直接对发动机-旋翼轴-主旋翼整体进行倾斜角度控制,省去了大量微小的高速转动的传动结构,在增大了整体重量的同时,降低了制造的技术难度和故障率。

图1 倾斜旋翼轴示意图
周期变距方案通过改变不同位置的桨距,结合桨叶挥舞来改变拉力方向。与周期变距方案不同,倾斜旋翼轴方案通过使用伺服系统直接改变旋翼盘法线方向来改变拉力方向,进而得到平动的分力。对于无人机而言,相对于周期变距方案,倾斜旋翼轴需要功率更大的伺服系统对发动机-旋翼轴-主旋翼整体进行姿态控制,但是有更加简单易维护的机械结构。并且与应用在载人直升机上不同,将该方案应用于轻型航模直升机不会带来诸如共振等潜在的安全隐患[4]。
2 容积卡尔曼滤波姿态解算
在本设计中需要处理分别来自加速度计和陀螺仪的加速度数据和角度数据,最终求得无人机平台的位置和运动状态,姿态解算与控制流程如图2 所示。在这些数据中,含有白噪声、振动等由传感器性能和工作环境导致的误差及其他随机干扰。需要使用滤波算法尽可能准确地还原出掩盖在噪声下的真实数据,以使后续对无人机平台的姿态控制能够更加精确。由于本设计所使用的传感器数据噪声主要为高斯白噪声,含有少量非高斯随机噪声,无人机的姿态信卢融合为非线性问题,同时考虑到低功耗微处理器对实时计算量的限制,最终选定容积卡尔曼算法作为主要滤波算法[5-6]。
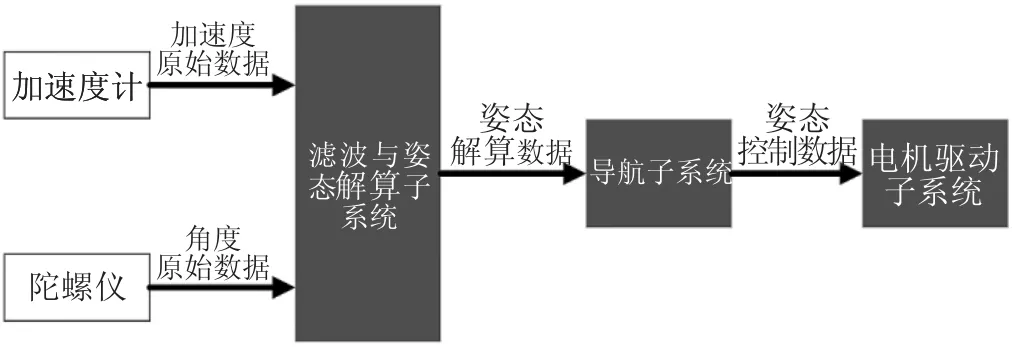
图2 姿态解算与控制流程
2.1 解算加速度原始数据
加速度计输出的是在机体坐标系下的三轴加速度,由加速度计测量重力方向可解算出俯仰角、横滚角、偏航角。在机体坐标系中,设加速度计的输出为an=[axayaz]T,加速度计的输出与姿态角的关系如式(1)所示。
当机体坐标系相对地理坐标系处于静止的状态下时,可以将其归一化得到地理坐标系下的重力向量Gn=[0 0 -1]T。通过姿态矩阵c1可以转化地理坐标系与机体坐标系的数据,从而计算出姿态角。
根据式(2)(3),代入加速度计在机体坐标系下的输出得到基于重力向量计算的俯仰角θ 与横滚角γ。
根据式(4),将加速度计计算的俯仰角θ 与横滚角γ 代入式(5),得到偏航角ψ 如式(6)所示。
同时,初始四元数的计算可以由加速度计解算出的机体坐标系下的姿态角转化得到,其转换方式如式(7)所示。
2.2 解算角度原始数据
利用陀螺仪所获取的信卢,通过龙格库塔算法更新为四元数,将得到的四元数作为预测数,把加速度仪的数作为测量值。式(8)为陀螺仪输出的三轴角速率。
采用一阶龙格库塔法求解常微分方程式(9),式(9)中x 如式(10)所示,Ω 如式(11)所示,由此得系统的状态方程如式(12)所示。
当机体坐标系与地理坐标系相互垂直时,加速度计输出的基于机体坐标系下的加速度如式(13)所示。通过方向余弦矩阵法可求得量测方程如式(14)所示。
2.3 容积卡尔曼滤波姿态解算
四旋翼无人机的飞行姿态信卢融合模型为一种非线性动力学问题,其离散时间的飞行状态空间模型定义如式(15)所示。
将修正的四元数归一化处理后再用来计算求解的姿态角,其计算的公式如式(16)所示。
最终得到的姿态角计算结果将传递至导航子系统中。
3 自适应PID 算法姿态控制
PID 控制理论是当今一种最具广泛商业应用潜力的先进控制分析方法,其重要的理论优点是用户不需要深入了解每个被控分析对象,无需对其建立精确可靠的系统数学模型、进行复杂严密的系统理论计算,只需要根据被控变量参数与系统给定值参数之间产生的时间偏差系数及时间偏差值的变化率等2 个简单控制参数,对比例系数、积分时间和微分时间偏差3 个主要参数值进行动态调整,一般情况下均可以得到较为理想的控制效果[7]。
然而由于无人机的强非线性的控制特点与无人机运行时存在危险性、风洞实验设备昂贵、真机调试成本高等现实问题,对于无人机平台的姿态控制难以实现PID 控制参数的整定。而基于深度学习[8]、群智能算法[9]等的现代控制算法在仿真过程中有很好的表现,但由于其计算量大,在算力有限的无人机机载微处理器中得不到理想的控制效果。因此本设计采用双闭环并级PID 与模糊控制协同的飞行姿态控制算法,如图3 所示。

图3 自适应PID 控制算法
首先解耦方程如式(17)(18)所示。
飞行姿态控制双闭环控制方案中的角度环PID 控制部分采用并级PID[10]。偏差公式如式(19)所示。其中ra(k)为输入角度环PID 控制器的期望角度值,ca(k)为输入角度环PID 控制器的实际角度值。
控制规律如式(20)(21)(22)所示。其中Kpg为角度环比例系数、Kig为角度环积分系数、Kdg为角度环微分系数。Kpg、Kig、Kdg的取值均需要在飞行试验过程中整定。
在双闭环控制方案中,输入角度环PID 的期望角度值为外环PID 的输出值uc(k),设实际角速度值为cr(k),则输出控制偏差值如式(23)所示。其控制规律如式(24)(25)(26)所示。其中Kpf为内环比例系数、Kif为内环积分系数、Kdf为内环微分系数。
Kpf、Kif、Kdf的取值由现场整定部分和模糊控制器的输出部分组成,如式(27)(28)(29)所示。式中,kpf、kif、kdf的取值需要根据现场飞行试验中的数据整定,Δkpf、Δkif、Δkdf为模糊控制器的输出。
最终计算结果将传递给舵机驱动子系统将其转化为驱动舵机的信号。
4 姿态控制仿真分析
使用MATLAB 仿真环境下的SIMULINK 工具,搭建串级PID 与模糊控制相结合的半自适应控制算法仿真模型。选择阶跃信号作为输入信号。初始角速率设置为0,以横滚角为分析对象,比较提出的自适应PID 算法与一般PID 算法的控制效果。运行仿真模型,期望角度为30°时,飞行姿态在阶跃输入信号下的仿真结果对比如图4 所示。

图4 控制效果对比
从仿真结果可以看出,相较于PID 算法,串级PID与模糊控制相结合的自适应PID 控制算法能够对姿态角进行更为理想的控制,能够达到稳定且收敛的仿真结果,证明该自适应控制算法对共轴无人机的飞行姿态具有良好的控制能力。
5 结束语
本项目针对目前无人机续航能力、自稳定性能瓶颈凸显,无人机长续航设计和强抗风设计矛盾无法调和的情况,设计一款基于容积卡尔曼滤波-自适应PID的共轴反桨无人机,采用与普通多旋翼不同的气动布局,尝试得到更长的续航时间与更理想的悬停稳定性。本设计在对传感器信号的处理上使用了容积卡尔曼滤波算法,在对姿态的控制上使用了自适应PID 算法,以期望无人机有更好的稳定性。通过仿真测试,试验结果表明,基于容积卡尔曼滤波-自适应PID 的共轴反桨无人机具有良好的姿态控制能力。

