基于变量分层的CFRP结构件宏细观协同优化设计方法

倪伟，周金宇，王志凌，韩文钦

（1.江苏理工学院机械工程学院，江苏 常州 213001；2.金陵科技学院机电工程学院，江苏 南京 211169）

1 引言

碳纤维复合材料（CFRP）的宏细观协同优化是一种综合考虑结构优化与材料铺层优化来提高CFRP结构件性能的优化设计方法。优化设计分为独立优化和一体化优化，其中一体化优化又分为整体优化和协同优化。基于变量分层的宏细观协同优化是将优化问题分为系统层面与子层面，子层面包括结构层面与材料层面，在子层面中设置暂态变量与惩罚项，通过减少系统层面的设计变量实现模型降维，从而提高算法收敛效率。

针对宏细观协同优化设计，国内外学者已取得诸多研究成果。例如：文献[1]通过缩减求解空间，将系统级非线性等式约束变换为只含有变量边界的线性不等式约束，解决了传统协同优化求解困难的问题；文献[2]采用变量解耦法，提高了多学科协同优化的收敛效率；文献[3]将范数与动态松弛系数引入汽车车身的协同优化设计中，提高了协同优化效率；文献[4]采用结构材料协同优化方法实现了压力容器的优化设计；文献[5]使用人工神经网络改进多目标协同优化设计，采用反向传播算法对神经网络元模型进行训练，极大的提高了算法优化效率；文献[6]提出了一种基于模糊偏好函数的多层面协同优化方法，采用改进的遗传算法进行协同优化设计，提高了协同优化设计的鲁棒性。

针对CFRP结构件宏细观协同优化设计[7]过程中由于设计变量较多导致收敛慢的问题，提出基于变量分层的协同优化设计方法，并将该方法其运用到汽车CFRP顶盖的优化设计中。宏观结构层面根据顶盖的功能要求进行NURBS曲线的结构优化设计，细观材料层面对CFRP铺层角度与铺层厚度进行优化设计，提取顶盖总厚度作为系统层面的公共变量。系统层面采用自适应遗传算法（AGA）进行协同优化设计，汽车顶盖轻量化的同时提高顶盖的固有频率从而避开激励源频率和声腔模态频率，达到顶盖减振的效果。

2 宏观结构优化设计

2.1 宏观结构轮廓的NURBS描述

曲面造型采用NURBS 建模，NURBS（Non Uniform Rational B−Spline）通常称为非均匀有理B样条曲线，是常用的自由曲线建模方法。NURBS高精度、高光顺的特点使其在结构优化设计中占据重要地位。

NURBS曲线可以定义为：

式中：Vi—控制顶点；ωi—权因子；Bi，（ku）—节点矢量U=[u0，u1，…，um]上的k次NURBS基函数，通常情况下u0=u1=…=ui=0，ui=ui+1=…=um=1；ui（i=0，1，…，m）—节点，为确保NURBS曲线的凸包性，要求ωi≥0。

通过调整NURBS曲线的控制顶点xi及其权因子ωi从而实现结构优化设计，结构层面的NURBS 曲线优化设计完成后，将NURBS 曲线的节点坐标以APDL 命令流的形式输入到ANSYS中，并拟合成CFRP结构件的截面曲线，CFRP结构件的有限元模型则由截面沿NURBS曲线方向扫略而成。

2.2 强度失效准则

CFRP结构件采用Tsai−Wu失效准则[8]作为失效判据。

其中，左边多项式大于1，材料发生破坏。F1、F11、F12、F2、F22、F66为6个独立的强度参数，其计算公式如下：

式中：XT—纤维方向拉伸强度极限；XC—纤维方向压缩强度极限；

YT—垂直纤维方向拉伸强度；YC—垂直纤维方向压缩强度；

S—剪切强度极限，均可由实验测得。

2.3 宏观结构优化设计的数学模型

以CFRP结构件质量最小为设计目标，结构件的截面轮廓控制节点xi及其权因子ωi作为结构层面的设计变量，使用APDL语言进行结构参数化建模与分析，采用Matlab编制优化主程序并调用APDL参数化建模与分析的txt结果文件进行优化设计，其数学模型为：

式中：目标函数M1表示CFRP结构件的质量；ω1，…，ωm—NURBS曲线控制点的权因子；x1，…，xm—NURBS 轮廓曲线控制点横坐标；d1—结构层面的离散型暂态变量；[ai,bi]—NURBS曲线控制点的横坐标区间；g1—强度失效判据，等于式（2）左边的值。

3 细观铺层优化设计

3.1 细观CFRP铺层设计准则

CFRP铺层优化设计中，影响CFRP性能的因素主要有铺层角度和铺层厚度，材料层面中以铺层角度与铺层厚度为设计变量进行优化设计。

CFRP铺层优化设计的要求如下：

（1）CFRP铺层角度通常取−45°、0°、45°、90°四种；

（2）考虑到CFRP 的层间裂纹、制造工艺约束条件以及应力集中的情况，碳纤维不可连续铺放（3～4）层；

（3）4种角度应满足的铺层层数要求是，0°与90°铺层占比为（10～30）%，±45°铺层占为（20～50）%。

3.2 细观铺层优化设计的数学模型

材料层面中，CFRP的固有频率为设计目标，CFRP铺层角度与铺层厚度作为设计变量。采用自适应遗传算法求解数学模型，材料层面优化设计的数学模型为：

式中：f—目标函数，表示CFRP铺层优化后的结构件固有频率，由ANSYS求得。θ1，…，θn—CFRP的各铺层角度；d2—材料层面的离散型暂态变量；dp—定值，表示CFRP 层单元厚度。总铺层数n可通过d2/dp表示，为减少固化变形，采用对称铺层；n—偶数；g1—强度失效判据；e、r、p、h—0°、−45°、45°和90°铺层角度的铺层数。

4 宏细观整体优化

4.1 宏细观整体优化算法

宏细观整体优化法的设计变量通常包含全体子层面设计变量。对于离散型设计变量往往采用遗传算法进行优化设计，自适应遗传算法更具备良好的全局收敛能力，使其在求解协同优化设计问题中广泛应用。

例如：文献[9]在整体优化设计的过程中，设计变量包含结构与材料层面的所有变量。采用Matlab编制遗传算法优化主程序，使用APDL语言进行参数化建模与分析，通过Matlab与ANSYS的相互调用实现宏细观整体优化设计。

4.2 宏细观整体优化设计的数学模型

宏细观整体优化法首先在结构层面与材料层面建立初始变量参数，使用APDL语言完成参数化建模并保存分析结果数据为txt文件，采用Matlab编制优化主程序，调用APDL命令流并读取分析结果txt文件，若满足收敛要求，则输出优化结果。否则修改结构层面与材料层面的初始变量参数，进入循环计算直至满足收敛要求后，输出优化结果。其数学模型为：

式中：M2—目标函数，表示整体优化法的CFRP 结构件质量；ω1，…，ωm—NURBS 曲线控制点的权因子；x1…xm—NURBS 控制点横坐标；d—离散型变量，表示CFRP结构件的总厚度；θ1，…，θn—CFRP的各铺层角度；ai、bi—NURBS曲线控制点横坐标的区间；g1—强度失效判据；n—碳纤维铺层总层数；e、r、p、h—0°、−45°、45°和90°铺层角度的铺层数，CFRP的层单元厚度为定值。

5 基于变量分层的宏细观协同优化

5.1 变量分层的基本思想

针对宏细观协同优化设计过程中由于设计变量较多导致收敛慢的问题，采用变量分层对设计变量进行分层处理，将设计变量统称为协同优化变量，协同优化变量分为全局变量与局部变量（ωi、xi、θk），全局变量分为公共变量d与耦合变量Y。

这样，宏细观协同优化系统层面中的设计变量只包含公共变量与耦合变量，耦合变量Y相当于固有频率、强度等，可由局部变量与公共变量复合而得，对于具体的工程实例，耦合变量可通过有限元软件求得。

各子层面内包含局部变量与暂态变量di，在子层面的目标函数中加入体现暂态变量与公共变量差异的惩罚项，确保公共变量的优化结果一致。

5.2 基于变量分层的层面优化设计

变量分层的协同优化分为系统层面优化与子层面优化，子层面包含结构层面与材料层面。

结构层面中，结构件质量最小作为设计目标，结构件的截面轮廓控制节点xi及其权因子ωi作为结构层面的局部变量，结构件厚度d1作为结构层面暂态变量进行优化设计。材料层面中，CFRP铺层固有频率最大作为设计目标，CFRP的铺层角度θk作为材料层面的局部变量，结构件铺层厚度d2作为材料层面暂态变量进行优化设计。系统层面中，全局变量包含公共变量与耦合变量[10]，CFRP结构件质量最小作为系统层面设计目标进行优化设计。

5.3 基于变量分层的协同优化设计

采用分层协同优化法求解协同优化问题时，将宏细观协同优化分为系统层面优化与子层面优化，子层面优化包含结构层面优化与材料层面优化，变量分层的设计框架以及数据传递，如图1所示。

图1 基于变量分层的协同优化框架Fig.1 Collaborative Optimization Framework Based on Variable Stratification

图1的系统层面中，在确保耦合变量一致的情况下，对CFRP结构件的质量进行优化设计。d—系统层面的离散型公共变量，表示结构件总厚度。Y—耦合变量，表示CFRP结构件的固有频率。Yi—各层面的耦合变量；Ai—公共变量与耦合变量的计算模型；g1为强度失效判据；|d−di|2=0—迫使各子层面暂态变量与系统层面公共变量差异最小的惩罚项。

ωi、xi—结构层面的局部变量；d1—离散型暂态变量，表示结构层面预设的结构件总厚度。δ1—统一子层面优化目标量纲的系数；[a，b]—NURBS 曲线控制点的横坐标区间；g1—强度失效判据；Y1—结构层面的耦合变量，表示固有频率，由ANSYS 求得。A1—结构层面中由局部变量（ωi，x）i与暂态变量d1求出的固有频率。

θk—材料层面的局部变量；d2—离散型暂态变量，表示材料层面预设的CFRP铺层总厚度；δ2—统一子层面优化目标量纲的系数；dp—定值，表示CFRP层单元厚度，总铺层数n可通过d2/dp表示，为满足对称铺层要求，n—偶数；g1—强度失效判据；e、r、p、h分别代表0°、−45°、45°和90°铺层角度的铺层数；Y2—材料层面的耦合变量，表示固有频率。A2—材料层面中由局部变量θk与暂态变量d2求出的固有频率。

各子层面对层面内的局部变量与暂态变量进行优化设计，将局部变量与暂态变量的最优解传递到系统层面求解全局变量。系统层面将全局变量最优解d*、传递回子层面，更新子层面中的暂态变量di。与整体优化法相比，基于变量分层的协同优化设计方法的不同之处在于：

（1）分层协同优化法可在子层面中分别建立数学模型并进行独立优化设计。

（2）各层面中包含耦合变量的约束条件，可确保耦合变量优化结果的一致性。

（3）在子层面的目标函数中加入惩罚项，可迫使子层面中暂态变量与系统层面中公共变量的优化结果最终趋于一致。

（4）系统层面包含公共变量与耦合变量，减少系统层面中的设计变量实现模型降维，提高算法收敛效率。

6 优化算例

6.1 问题描述

以汽车CFRP顶盖为例，复合材料采用YPH−209环氧树脂作为基体，选择T300型碳纤维作为增强纤维，汽车CFRP顶盖几何尺寸长宽厚的初始值为（1295×1085×6）mm，CFRP层单元厚度为0.25mm，CFRP初始总铺层数为24层。实现汽车顶盖轻量化设计的同时提高其减振性能，并与原先采用的钢制汽车顶盖作对比。

6.2 协同优化过程

CFRP顶盖的宏细观协同优化设计包含相互耦合的结构层面与材料层面。截面横坐标xi的初始节点坐标为[15 190 480 1295]，预设的暂态变量d1取值为6mm。如图2所示，顶盖的NURBS初始权因子ω=[1 1 1 1]，结构层面优化后的权因子为[1 0.7611 0.7424 1]，截面横坐标优化结果为[15 206.65 465.48 1295]，结构层面的暂态变量d1优化结果为6mm。

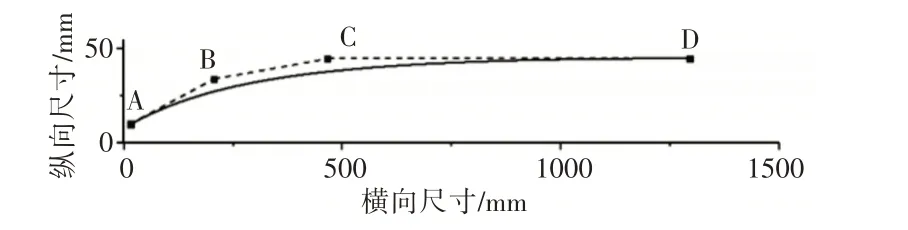
图2 顶盖截面的NURBS结构优化设计Fig.2 The Optimal Design of NURBS Structure for Car Roof

材料层面中，采用遗传算法对CFRP 铺层角度进行优化设计，CFRP顶盖铺层采取对称铺设，预设的材料铺层厚度暂态变量d2为6mm，初始铺层为[−45/0/45/90]3s，得到材料层面的暂态变量d2优化结果为7mm。

系统层面的优化设计中，局部变量与暂态变量为各子层面的最优解，将系统层面优化得到的总厚度d与固有频率Y的最优解反馈回子层面，通过子层面目标函数中的惩罚项更新子层面的暂态变量di，得到公共变量d的全局最优解为6mm。

采用整体优化法和分层协同优化法求解算例，从收敛次数上判断分层协同优化法的快速收敛性，以整体优化法的设计结果为基准，根据结果误差判断两种方法的精度。如图3所示，基于变量分层的协同优化设计迭代40次左右收敛。

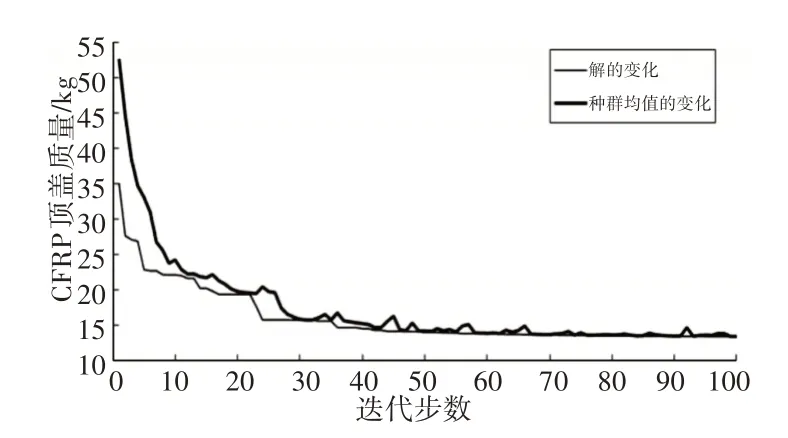
图3 基于变量分层的协同优化迭代过程Fig.3 The Collaborative Optimization Iterative Process Based on Variable Stratification

采用ANSYS验证优化结果，从图4可以看出，原先采用的钢制顶盖在固有频率为84.81Hz振动下的最大变形为0.3mm。从图5可以看出，宏细观协同优化后的CFRP顶盖在191.243Hz固有频率振动下的最大变形为0.67mm。

图4 钢制顶盖模态振型图Fig.4 Modal Shape of Car Steel Roof

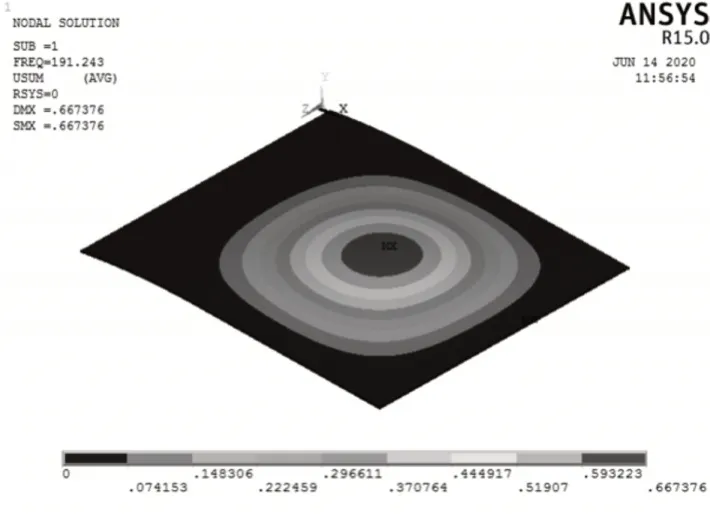
图5 协同优化后CFRP顶盖模态振型图Fig.5 Modal Shape of Car CFRP Roof After Collaborative Optimization

两种不同方法的CFRP顶盖优化结果，如表1所示。与原先采用的钢制顶盖相比，质量从66.18kg 下降至16.86kg，降幅为74.5%，CFRP 顶盖固有频率从84.81Hz提高至191.24Hz，增幅为125.5%，优化效果显著。与整体优化法相比，分层协同优化法的迭代次数降幅为51.2%。

表1 两种优化设计方法的结果对比Tab.1 Comparison Results of Two Optimization Design Methods

7 结论

（1）针对CFRP结构件宏细观协同优化设计中由于设计变量较多导致收敛慢的问题，提出分层协同优化法，该方法能够提高此类优化设计的收敛效率并确保结果的准确性。（2）根据汽车CFRP顶盖的减振要求进行NURBS结构优化设计，为解决此类自由曲面结构优化设计问题提供思路。