自适应GA−WAF盲源分离用于滚动轴承故障诊断

张玉安，陆正刚，王小超

（同济大学铁道与城市轨道交通研究院，201804 上海）

1 引言

铁路货车轴承故障诊断困难，但是一旦出现问题就会造成巨大的损失，因此针对早期故障、复合故障以及对轴承的寿命预测问题，成为近年来的研究热点。

独立分量分析（Independent Component Analysis，ICA）是盲信号提取（Blind Source sSeparation，BSS）的基础算法，通过总结当前已有的ICA方法，可以发现他们都是利用不同的目标函数和优化算法组合，提取出想要的成分[1]，因而得到使用与推广。为了弥补该方法数据的信息的利用不够充分等问题，优化提出了CI⁃CA方法[2]，最大的优势就是不需要知道源信号的数目，依照已有的信息设立参考信号，提出期望的独立分量，计算量小，弥补了ICA算法的不足。利用盲源分离理论有一定的成效，但是强噪声下，采取某些信号降噪方法处理后，可以进一步提高诊断结果。

对于滚动轴承故障诊断滤波问题，固定参数的滤波器凭经验选择，缺少自适应性，为了找到一种自动化方法选择带通滤波参数，选择遗传算法（Genetic Algorithm，GA）进行优化，该算法能寻求全局最优解，避免了传统的最速下降法和共扼方向法等导致局部最小和最大的问题；计算量不大，避免了柔性多面体方法需要大量计算的问题；性能可靠，避免了神经网络结构对性能的影响非常大的问题。

平滑信号的检测一般采用小波分解，对于轴承故障等冲击类特征检测一般可以采用小波滤波，考虑到轴承的故障冲击产生的瞬态与Morlet小波非常相似[3]，所以选择Morlet小波滤波器（Wave⁃let Analysis Filter，WAF）进行解调和降噪，提出以信号的峰值因数为适应函数的遗传算法的改进小波滤波器。

与传统的解调方法相比，Teager 能量算子（Teager Energy Operator，TEO）对瞬态的能量非常敏感，可以突出产生故障的冲击成分，解调的精度更高，运算速度更快，文献[4]中说明了该方法对故障解调的适应性，因此采用TEO分析。

考虑到以上方法各自的优越性，提出了自以峰值因数为目标函数的适应GA−WAF的多通道CICA方法，并经过仿真和试验多次对照验证该办法。

2 基于遗传算法的带通滤波器的设计方法

遗传算法通过以下步骤进行，关键是选择合适的滤波器、滤波器的编码方法以及评价函数的选择。

2.1 滤波器的选择

轴承的故障冲击产生的瞬态与Morlet小波非常相似，选择复Morlet小波进行改进的设计，它在频域具有高斯窗的形态[3]，其定义为式：

则它的傅里叶变换为：

式中：f0—中心频率；σ—带宽

那么小波滤波器可以构造为：

它的频带范围为[f0−σ/2，f0+σ/2]，X(f)只需要计算一次，U*(f)对所有范围内的f0和σ进行计算，具有较快的计算速度。

为了满足零均值、采样定理、带宽充分大等要求，选择最优参数时同时需要满足［5］：

式中：fs—采样频率；fr—轴的旋转频率；fd—故障频率，这样确定了中心频率和带宽搜索的范围，便于滤波器参数的编码。

2.2 滤波器参数的编码

采用基于二进制的基因型编码的方法，一旦滤波器的基因确定，则滤波器参数完全确定。设定精度为1，使用25位表示一个小波滤波器，其中中心频率选择为13位，带宽选择为12位。则

式中：f0—中心频率；σ—带宽；chrom（i）—基因型的二进制位。

2.3 遗传算法的运算

选择好了滤波器，确定好了基因编码方法，遗传算法实现步骤为：

2.3.1 初始化基因组

首先创建一个随机种群，综合考虑收敛速度和计算量，个体数目N一般选择在（40～100）范围内，这里N选择为60。

2.3.2 评价函数（适应度）的确定

评价函数是选择的决定因素，遗传到下一代的概率取决于基因组的评价函数值，如果仅仅选择一种参数作为评价函数具有一定的局限性，因此必须尽可能的多选择的参数，选择峰值因数值标，既反映峰值，又反映RMS值，故障越大，峰值因数越大，对于信号x（t）定义峰值因数为：

2.3.3 遗传

将N个父本基因中，适应度概率高于P（s遗传基因）的几个基因，由父代复制子代，构成子代基因。适应度概率的计算公式为：

2.3.4 交叉

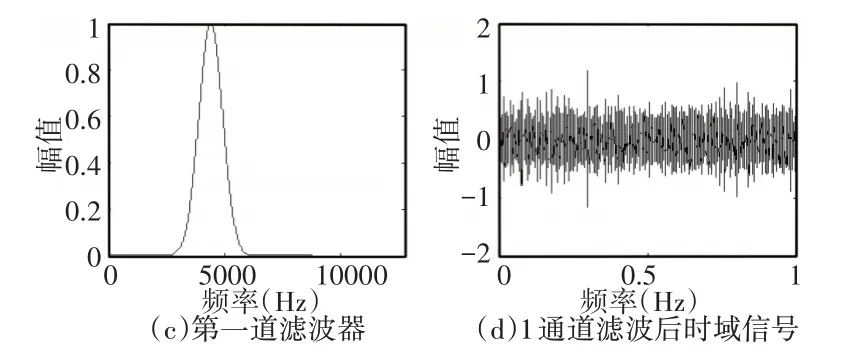
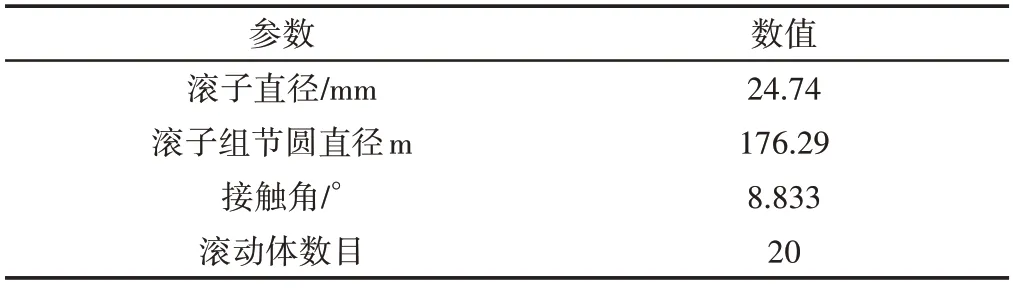
选择在N个父代基因中，根据交叉概率Pc，随机选取N*Pc/2对父代基因，且对每一对基因，随产生（1～25）中的两个随机数N1、N（2N1

2.3.5 变异

选择变异数量为Pm*N，Pm选择为0.01。

2.3.6 终止条件

终止原则为最大遗传代数，选择为100代，也就是100代进化后，其数值不再变化，遗传算法流程图，如图1所示。

图1 遗传算法流程图Fig.1 Flow Chart of Genetic Algorithm

3 基于CICA的盲信号提取方法

盲信号提取实质上是利用目标函数和优化算法求解一个解混矩阵W，将待提取的目标信号y从观测信号中分离出来。目标函数与优化算法的不同构成了不同基于的盲信号提取算法。

一方面，考虑到负熵的鲁棒性比峭度好，梯度法、牛顿法的速度和计算的复杂性，选择负熵为目标函数，乘子算法为优化算法，如式（10）所示。另一方面，为了避免ICA算法中源信号数目未知的问题，引入了新的CICA算法。它将源信号作为参考信号（约束函数）r(t)，将待提取的目标成分y和参考信号r(t)的距离定义为ε(y，r)，计算量更小［6−7］，该算法的数学模型为目标函数：

约束条件：

式中：ρ—正常数；G（·）—非线性函数；v—高斯变量，与目标成分y有相同协方差矩阵；ξ—阈值；ε(y，r)=E{(y−r)2}用以表示目标成分和参考信号的接近程度［10］。

为了使盲信号提取算法收敛，所构建的参考信号r(t)有一定的要求，文献［2］建立的模型，利用轴承故障频率作为参考先验信息，构造具有非高斯性的脉冲信号作为参考信号，基于该模型建立约束函数。

4 基于GA−WAF和CICA的盲源分离方法

为了提取目标信号，提出基于遗传算法改进的小波滤波器和CICA的盲源分离方法，具体流程图，如图2所示。

图2 故障诊断流程图Fig.2 Flow Chart of Fault Diagnosis

首先将采集到的多通道振动信号通过改进的小波滤波器进行降噪，具体参数由改进的遗传算法自适应选择，提高故障信号信噪比，然后将滤波后的信号输入负熵为目标函数，乘子算法为优化算法的CICA方法识别故障特征，最后利用TEO解调。

5 仿真分析

为了验证上述方法的有效性，构造滚动轴承单点故障振动信号的仿真模型，如式（14）所示。

式中：选择位移常数y0=3、阻尼系数g=0.1、固有频率fn=4.5kHz、采样频率fs=20kHz、单周期采样时刻t0，重复周期0.02s，采样点数为25600，添加一定的高斯白噪声，模拟强噪声下采集到的早期故障信号。

原始形成两个仿真通道信号，它们的时域图和幅值图，如图3所示。

图3 两个仿真通道信号时频图Fig.3 The Time−Frequency Diagram of Two Simulated Channel Signals

能够发现，时域波形中存在着间歇性冲击，因为强噪声的污染，信噪比较低，无法识别其中的故障冲击成分，这模拟的就是采集到的原始故障信号。

对两组数据不进行处理，直接进行TEO 解调，如图4 所示。两个通道均无法正确找到故障频率，这也就显示了降噪的重要性。首先进行降噪处理，以通道1仿真信号为例，以峰值因数为目标函数，经过该新方法改进得到的小波滤波器带通滤波后，可以看出振动冲击得到了增强，如图5（b）所示。

图4 直接解调分析包络谱图Fig.4 Envelope Spectrogram of Demodulation Analysis

图5 仿真通道滤波后信号Fig.5 The Filtered Signal of Simulated Channel

图6 仿真通道滤波后解调包络图Fig.6 Envelope Spectrogram of the Filtered Simulated Channel Signal

对滤波后的信号进行TEO分析，可以找到预设的故障频率50Hz，而且此频率十分明显，这是因为带通滤波后过滤掉了大量的噪声信号，验证了该滤波方法是有效的，但是倍频等信息较弱。文献[2]构造具有非高斯性的脉冲信号的方法，选择轴承故障频率作为参考信号，选择方波信号，如图7（a）所示。

将预处理过后的两个通道的信号输入CICA方法，根据该方法原理，经过随机矩阵A混合，得到混合信号，再利用参考信号，该方法分离出来的信号时域图，如图7（b）所示。与图5（b）相比，振动特征进一步得到了增强，对分离出的目标信号做TEO分析结果，如图8所示。从图中可明显地看到对应的轴承仿真故障频率50Hz以及倍频，倍频十分明显，通过三次对比，逐步验证了该新方法有效解决了早期故障问题。

图7 分离信号Fig.7 The Separated Signal

图8 仿真通道算法包络图Fig.8 Envelope Spectrogram of Simulated Channel’s Algorithm

6 实际验证

接下来，以轨道车辆轴箱轴承为实验对象，采用单轮对跑合试验台对所提轴承故障诊断方法进行验证，如图9所示。铁路货车轴承一般为双列圆锥滚子轴承，选择实验轴承为双列圆锥滚子轴承（型号为SKF197726），轴承结构参数，如表1所示。设计故障为外圈故障，故障位置和大小如图所示，依照表1计算得到的外圈故障频率为67Hz。实验转速为456r/min，采样频率为25600Hz，选取1s数据进行分析。

表1 故障轴承几何参数Tab.1 Geometric Parameters of Fault Bearing

图9 故障轴承及传感器的安装位置Fig.9 Location of Failure Bearing and The Sensor

采集到的两个振动试验信号，如图10所示。因噪声污染，想要得到的故障信号被复杂的噪声信号淹没，无法识别得到故障冲击成分。同样的，以通道1为例，采用基于遗传算法改进的滤波方法，对信号进行滤波预处理，如图11所示。同样对比发现振动信号得到了明显的加强，在图12可以找到对应的故障频率67Hz，也同样证明改进的滤波算法有效。

图10 两个实验通道信号的时频波形Fig.10 The Time−Frequency Diagram of Two Experimental Channel Signals

图11 一个实验通道滤波后信号Fig.11 The Filtered Signal of Experimental Channel

图12 实验通道滤波后包络谱图Fig.12 Envelope Spectrogram of the Experimental Channel Filtered Signal

接下来进行CICA算法分离处理，如图13所示。我们可以得到分离出来的故障信号时域图，和图11（b）对比，图15（b）很明显振动特征更加明显。对该分离出来的信号进行TEO解调分析，清楚得找到故障特征频率67Hz以及其他更多的倍频，并且倍频十分明显，可以证明基于自适应GA−WAF的多通道CICA方法的优越性和可行性。

图13 分离信号Fig.13 The Separated Signal

图14 实验通道算法包络图Fig.14 Envelope Spectrogram of Experimental Channel’s Algorithm

7 结论

为了解决CICA方法用于轴承早期故障诊断，以及选择共振频带时，单凭经验设置带通滤波参数的问题，提出了改进的自适应GA−WAF的多通道CICA方法，首先对采集到的信号进行滤波降噪，对传统滤波方法进行改进，提出以峰值因数为目标函数的遗传算法，使用25 位进行基因型编码，并应用到盲信号算法预处理上来，避免了经验选取参数，凸显出强噪声下的故障成分。在目标函数与优化算法不同的盲信号提取算法中，选取新发展起来的基于模型的CICA 方法，并选择负熵为目标函数，乘子算法为优化算法，计算量小，准确的反映故障特征。

数据多次对比证明，基于改进的小波滤波、CICA 方法相结合的盲信号提取故障诊断方法可以全面、准确地诊断出故障特征信息，为该领域提供新的方法。