体能运动训练器低频振动参数调节方法

张歆

（燕山大学体育学院，河北 秦皇岛 066004）

1 引言

体能是根据运动素质表现出的人体基本运动能力，是运动员竞技能力的重要组成部分。目前，运动员在体能训练过程中主要依托体能运动训练器进行训练[1]。体能运动训练器主要包括仰卧板、健身车、杠铃、椭圆机、踏步机、跑步机等。体能运动训练器能够满足人体关节多自由度的训练需求，但体能运动训练器自身的振动状况影响人体训练机体角度，过大的振动容易造成运动损伤。因此，如何控制体能运动训练器的振动状况是当前的研究重点之一。

目前，已有学者对体能训练器的相关控制方法进行了研究。文献[2]利用经验小波变换设定上肢力量训练器传递函数，通过对上肢力量训练器故障参数的提取，以此达到故障监测效果，可以有效提高上肢力量训练效果，但该方法的振动频率较大。文献[3]设计了康复训练器，优化控制线性自抗扰控制参数，设定速度自抗扰控制方法，提升训练器的负载能力，满足被动康复训练的需求，但该方法的训练质量较低。文献[4]设计了一种尖峰训练器，不同的运动轨迹根据设定不同会产生不同的生物力学反应，根据运动学和动力学原理提升运动激活指数，以此达到提升运动传感效果。

通过上述研究分析，可以得出设计一款训练器对于提升运动员的体能运动训练具有积极作用，调节振动参数以此减少低频振动现象，确保运动员体能训练效果，但方法的训练器协调性能较差。为此，提出了体能运动训练器低频振动参数调节方法。

计算体能运动训练器低频振动参数力学特征，运用遗传算法编码模式，明确训练器响应速率，运用等效质量法，推导出参数振动结果，实现振动控制参数调节，有效降低训练中出现的低频振动概率，提高训练器协调性能，达到高效体能训练效果。

2 体能运动训练器低频振动参数调节

训练器是体能运动训练中的关键设备，研究其振动动力方程对提升训练器整体性能极为重要。因为训练器是一个对称结构，获得训练器内某个振动片的动态特性，就能获悉训练器整体动力学性能。

在体能运动训练器受到反复驱动作用力时，会生成同周期振动现象[5]。这时作用在振动片角度φ处截面内的弯矩Mφ为：

式中：Iφ—转角处于φ的振动片惯性矩；E—训练器材料杨氏模量；R—驱动半径；d—振动片长度；v—振动片内的法向位移；w—振动片内的切向位移。

通过应力和应变关联获得振动片的法向力Nφ：

式中：w′—转角处于φ的截面大小；Aφ—是训练器材料厚度。

振动片在法向力与弯矩的协同作用下，生成的应变能为：

式中：M，N—角度φ的截面弯矩值，生成的动能为：

式中：μ(φ)—振动片线密度。

则振动周期T0：

式中：v″、w′—角度φ的微分。

由此，将振动片的振动方程组记作：

训练器半圆心张角通常要高于30°，若张角大于等于30°，低阶振动模态可使用非伸长型振动进行运算。这时不考虑振动过程中的轴向形变，则振动片内的法向位移v与切向位移w具有如下关联：

将v=w′引入式（6），简化方程组，得到：

通过式（8）即可明确体能运动训练器在不同频率下的动力学响应性能，以此判断体能运动训练器是否处于合理振动状态。

体能运动训练器涵盖镂空调节槽的调节支架、调节轮、电动机、凸轮和变频器。训练时要变更调节轮和凸轮的距离，持续调节振动幅度。将调节轮与凸轮当作需要调节的低频振动参数，对两个参数进行动力学建模分析，为达到最优体能训练效果提供数据支持。式（8）中包含t、φ两个变量，计算时要预先把时间改变的边界条件变换成和时间无关的边界条件[6−7]，剔除变量t。利用内力矩和外力之间的耦合关联，将振动片处于角度φ处截面内的弯矩Mφ重新定义为：

式中：M0—角度φ等于零的截面弯矩值。

通过训练器对称性可知，φ等于零的截面的转角也是零。由此获得角度φ处截面内的弯矩Mφ与驱动器动力F间的表达式：

将法向位移v与切向位移w分别描述成：

训练器端部位移计算公式为：

振幅放大比是衡量体能运动训练器振动幅度的关键指标，训练器振幅放大比越高，调节轮与凸轮之间的距离越大。将振幅放大比描述为：

等效质量算法就是将工程中真实拥有的若干集中质量或分布质量系统化简成一个具备等效质量的单独自由度系统的计算形式。采用等效质量法，计算调节轮与凸轮两个参数，设定两个参数能量与训练器能量相同，则参数等效质量为：

将式（15）变换为如式（16）所示的单参数微分方程组：

通过上述两个低频振动参数，为后续参数调节发挥重要作用。

3 遗传算法下体能运动训练器低频振动参数调节

使用遗传算法，完成体能运动训练器低频振动参数调节，使训练器依照不同的训练强度，最大限度提升训练器的协调性。首先对低频振动中的调节轮与凸轮两个低频振动参数进行编码设计。

编码是参数的一种参照生物学的表现形式，将参数涵盖的全部信息用相应的结构模式引入编码内，并把包含信息的编码命名为染色体[8]。输入与输出隶属度函数都是用对称三角形式，其变量为：三角顶点横坐标P，左右端点坐标U、V，三个变量中的两个变量随机组合均能决定隶属函数的最终形态。编码形式分析，如图1所示。

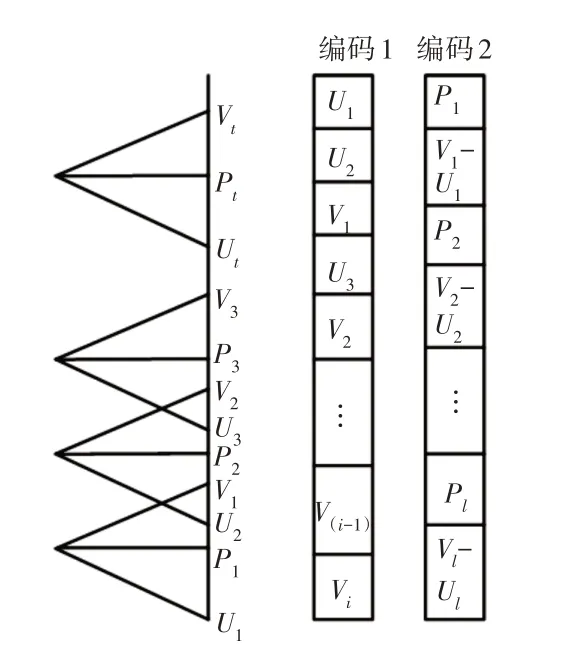
图1 编码形式分析Fig.1 Analysis of Coding Form

在图1中可知，其编码形式是一种重叠关联，也就是互相邻近的隶属函数1与2相交，不邻近隶属函数1与3不相交，这样就制约了隶属函数重叠率的改变幅度。

从隶属函数研究中看出：重叠率较小，则训练器响应速度加快，但在参数调节后期会发生振荡；重叠率较大，则训练器响应迟缓，但参数调节结果比较稳定。

只有较大面积的调节重叠率，才能符合低频振动参数调节的功能需求，即处于高振幅时期完成训练器快速响应，低振幅时期维持平稳。

遗传算法隶属函数的研究中，当前多数使用的是图1中的编码1形式。此类编码模式被广泛使用的原因在于，可以通过排序模式或增量编码形式确保变量维持以下次序：

利用式（17）随机输入点均具备非零隶属度。针对增量编码模式，在交叉后复原为绝对编码看出，交叉之后的特征和父代差距较多，因此使用排序模式完成参数编码设计。

图1内的编码2是关于训练器低频振动参数调节中使用的编码策略。编码内的P1，P2，…，Pi使用排序来维护隶属函数之间的位置关联。

隶属函数之间的重叠关联取决于自身的跨度系数(Vi−Ui)。此种编码模式的独立性包含了全部可能的邻近三角隶属函数的重叠关联［9］。与编码1的全部变量排序模式相比，能够优化排序过程中形成的隶属函数形变现象，保持振动参数调节可靠性。

式（18）的适应度函数展现了个体对应于体能训练器械的成效，此函数决定了个体在遗传算法内得到子代概率大小。

式中：ai(t)—第i个个体相对于时间t的振幅—振动参数调节的时间阈值；emax—全部e(i)内的最大值；f(i)—归一化之后第i个个体的适应度数值。为获得多种重叠率，采用编码2模式，那么需要处理编码1中不存在的问题，也就是低频振动子集收敛条件［10］。低频振动子集收敛条件阐明如下：针对处于论域X内的有限个低频振动子集而言，当且仅当满足式（19）情况下，能确保低频振动子集处于论域内随机点均不会发生Ui全部是0的状况，即保障随机输出引入至模糊推理中均具备一个稳定输出。

式中：Ui—输入x对应于第i个子集的隶属度。

下面分析低频振动参数调节过程。几类不满足收敛的个体振动衰退曲线，如图2所示。

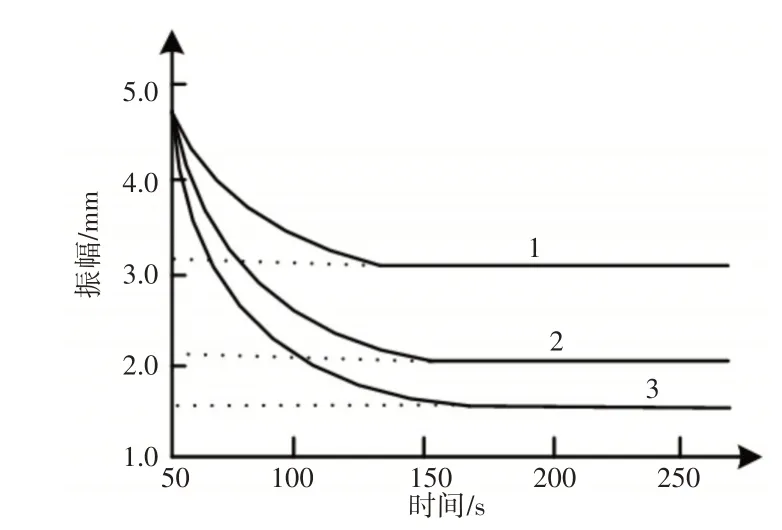
图2 不满足收敛的个体相对的振幅衰退性能Fig.2 Relative Amplitude Decay Performance of Individuals Not Satisfying Convergence

图2中，直线部分表示振幅振动参数进入Ui均为0的空挡后产生的失控状况。

1表示空挡产生于隶属函数曲线中间部分时的振幅抑制结果。从图中看出，幅值抵达空挡所处的3.2mm就不会继续下降，最终的回馈振幅为3.2mm。通过适应度函数计算可知此类空挡在适应度中获得较好表现，将此情况认定为恶劣状况。

2表示空挡产生于隶属函数曲线中后半部分时振幅的抑制结果。从图中发现，幅值抵达空挡所处的2.1mm就不再下降，最终的回馈振幅是2.1mm。但在抵达2.1mm之前，其振幅下降速度较快，与无空挡状况相比，其适应度也很高。

3表示一种最坏的空挡状况，其空挡位于振幅1.6mm，振幅下降至1.6mm时，由于空挡导致回馈振幅不再下降，展现出一种不存在振动的“优秀”特征。在遗传算法中，极易储存此类“优秀”个体，空挡个体无法得到剔除。此种个体适应度值很高，妨碍个体向最优参数调节的变换，有可能产生拥有空挡的伪参数组合，无法完成可靠的低频振动参数调节目标。

由此看出，只凭借适应度不能有效处理低频振动参数控制，而且在使用编码2实施遗传运算过程中，在交叉操作之后，极有可能生成不符合低频振动子集收敛条件的个体。振动参数调节的核心是引入一个收敛条件，防止振动过程中生成失调的隶属函数。收敛控制的根本目的是：对违背收敛的个体，挑选良好的基本并进行保存，并完善其余部分基因，去除Ui均是0的“空挡”。

设计一个收敛求解方法，采用独特的修补方法校准不可行解，该方法满足求解问题实际需求。计算过程为：将空挡左侧的隶属函数记作L，修正隶属函数L的峰值点与右支点，维持L的左支点和其他隶属函数不变，校准后的隶属函数的重叠率均为0.6。则低频振动参数调节的最终表达式为：

式中：Pnew—修正后的隶属函数峰值点；Bnew—修正后的隶属函数跨度；下角标new—隶属函数L；r—隶属函数。

利用式（20）调节控制后的低频振动参数，完成体能运动训练器低频振动参数调节。

4 实验结果分析

为了验证所提出的体能运动训练器低频振动参数调节方法的有效性，将PSD−BPA软件作为实验平台。选取跑步机作为体能运动训练器，利用压电式加速度传感器，结合振动测量技术，对低频振动信号进行采集。实验测试环境，如图3所示。

图3 实验测试环境Fig.3 Experimental Test Environment

在体能运动训练器低频振动参数调节过程中，以隶属度、低频振动信号频谱和时间阈值为测试指标对训练器的协调性能进行验证。

4.1 隶属度参数选择

隶属度是影响体能运动训练器振幅频率的重要参数，可以通过变更隶属度参数，降低训练中出现低频振动的概率。通过设定3组常见的隶属性参数数值，研究分析在训练中出现的低频振动情况，由此得出最优隶属度参数，具体结果，如图4所示。

分析图4可知，当训练次数为1000次时，隶属度为0.2时，具有较好的训练器控制效果，其振动频率为90Hz，可以达到运动员的运动强度。隶属度为0.4和0.6时，振动频率分别为38Hz和43Hz，均没有达到最优效果。由此说明，将体能运动训练器隶属度设定为0.2时，可以有效降低低频振动情况，提高训练器协调性能。

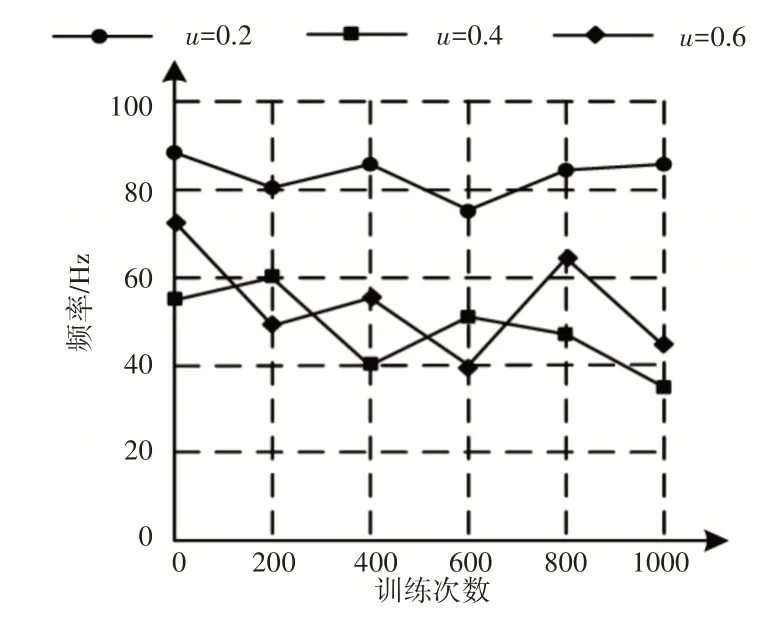
图4 不同隶属度频率结果Fig.4 Frequency Results of Different Membership Degrees

4.2 低频振动信号频谱分析

低频振动信号频谱特征可以在一定程度上代表体能运动训练器的振动状况。在设定最优隶属度参数后，研究频率与振动强度的关系，分析体能运动训练器在运动过程中产生的低频振动信号，由此生成信号频谱。通过信号频谱图，可以有效获取运动训练器在实际使用过程中的振动强度，以此作为调节依据，减缓低频振动现象。为了验证所提方法的低频振动概率，分别采用文献[2−3]方法进行对比，得到不同方法的体能运动训练器低频振动信号频谱，如图5所示。

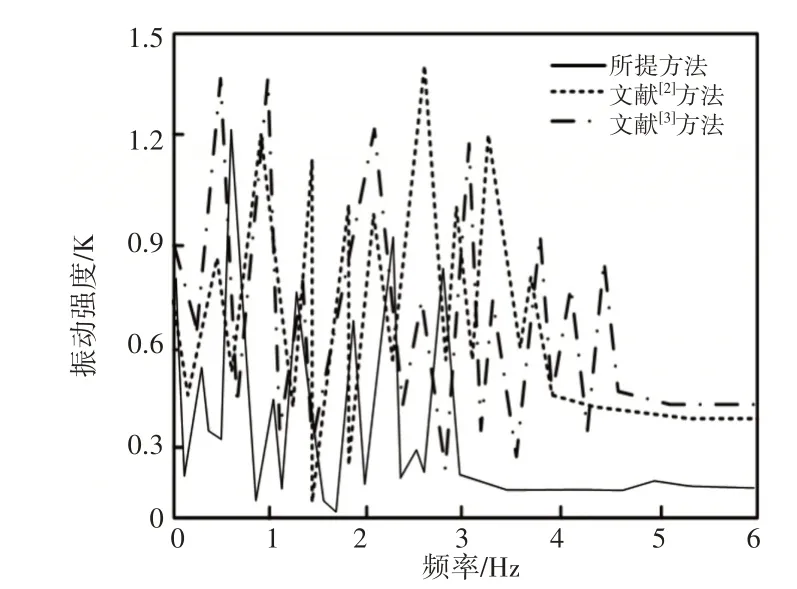
图5 不同方法的体能运动训练器低频振动信号频谱图Fig.5 Frequency Spectrum of Low−Frequency Vibration Signals of Physical Exercise Trainers with Different Methods

从图5可以看出，文献[2−3]方法的体能运动训练器工作时的振动频率分别处于（0～4）和（0～5）之间，而所提方法的体能运动训练器工作时的振动频率处于（0～3）之间。由此证明，所提出的体能运动训练器低频振动参数调节方法是有效的，符合真实场景的体能振动训练情况，能够有效降低训练中出现低频振动的概率，提高训练质量。

4.3 不同时间阈值下训练器协调性能测试

不同时间阈值条件下，训练器的振动频率及协调性能不同。测试训练器的协调性能有助于在最佳时间范围内对其进行控制或调整。

因此，对体能运动训练器设定5个时间阈值参数，通过1000次的训练次数，测试体能运动训练器的振动频率的稳定性，从而验证所提方法的体能运动训练器的协调性能。

分析表1可知，所提方法的体能运动训练器协调性能随着时间阈值的提高，其振动频率波动较小，整体较为稳定。由于利用了遗传算法关联了隶属函数的重叠，有效提高了训练器低频振动参数调节能力，以此达到高效体能训练效果。

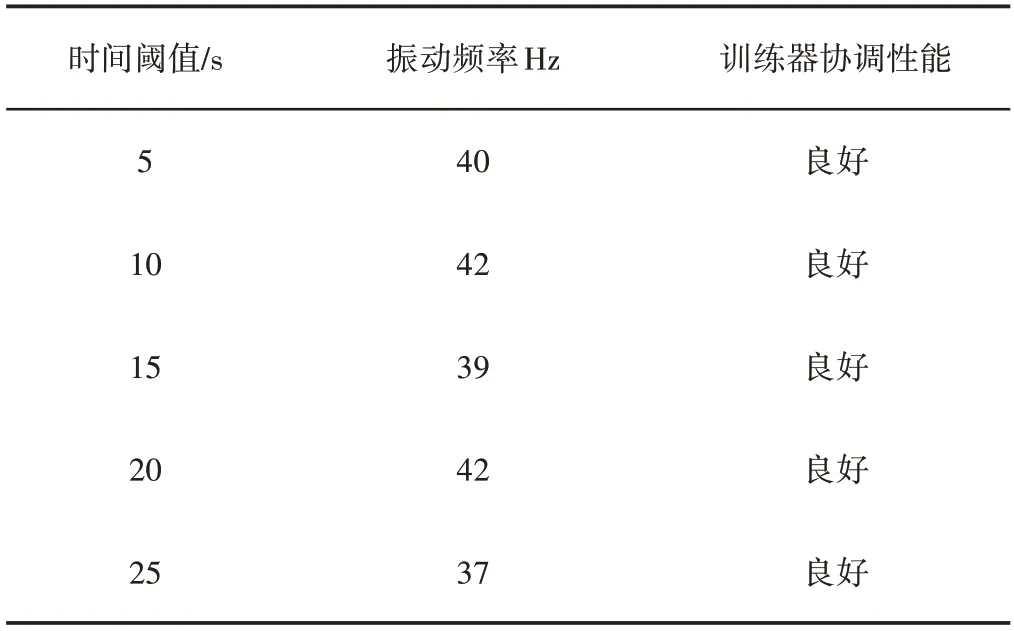
表1 不同时间阈值下训练器协调性能测试结果Tab.1 Coordination Performance Test Results of the Trainer Under Different Time Thresholds

5 结论

为了有效提高训练器的协调性能，提出了体能运动训练器低频振动参数调节方法。通过计算振动片截面弯矩，推导参数振动结果，引入遗传算法，实现低频振动参数调节。通过实验分析可知，所提方法可以有效降低低频振动情况，提高训练器协调性能和质量，为训练者提供一个良好的训练平台，达到高效体能训练效果。