基于射表的外弹道仿真模型的设计与实现
张明路,周志豪,黄俊卿,高春艳
(1.河北工业大学机械工程学院,天津 300130;2.陆军装甲兵学院演训中心,北京 100072)
1 引言
随着战争节奏加快与军事科技的日新月异,对炮兵武器系统操作熟练度要求越来越高,而实弹训练耗资巨大、风险性高、场地要求苛刻且组织实施繁琐,成为制约战斗员培养的一大难题[1],因此模拟化训练成为各国坦克训练的主要发展趋势,在训、战一致的逼真临境感与交互性效果下,通过模拟器反复练习,缩短训练周期的同时成本与危险性都大大降低,有效弥补实弹训练方式上存在的不足。
训练系统中外弹道模型是极其重要的部分,关乎系统设计合理与否,文献[2−3]应用六自由度刚体模型进行跨平台开发,体现飞行过程中弹体位置与姿态变化,但该模型在建立时就进行了种种假设,存在模型误差与运算复杂问题;文献[4−6]假定弹道空间为炮兵标准气象,应用质点微分方程组探究误差与散布影响因素,未考虑章动角(或攻角)、科式加速度与马格努斯力等力矩对外弹道影响,虽运算快速但难以满足系统仿真准确性要求[7]。
综上考虑,在进行合理假设简化后,以选定弹种基本射表中射角、坠落角、最大弹高等数据为基础拟合外弹道数学模型,并进行非标环境距离修正的方式,替代复杂的弹道微分方程分析求解。
该仿真方法不仅可以提高系统解算速度,满足实时性需求,而且能够灵活设定环境变量,搭建出不同训练科目的外部要素,解决传统微分方程组约束射击空间为标准气象条件与训练科目难以模拟战场环境的问题,使训练系统不再局限于提高炮兵对武器装备系统的使用熟练度,仿真性能大大提高,研究结果表明此仿真方法可以用于射击训练系统,并能为外弹道优化设计提供便利。
2 外弹道数学模型建立
结合理论计算与射击实验编制而成的射表被称为当前对空气外弹道最精确的描述,基本射表提供了标准气象条件下命中点与基本诸元的关系,与表定条件不符时,从修正射表读取变化值进行距离与射角修正,以修正距离为自变量从射表获取弹道信息,拟合炮口水平面与射击面的投影曲线,其中外弹道仿真流程,如图1所示。

图1 外弹道仿真流程图Fig.1 The Flow Chart of External Ballistic Simulation
2.1 射击距离修正
射表中查取散布、气温、药温、海拔高度、纵风、气压、初速、弹重偏差量[8]等非标准条件下对射击距离的修正量δ散布,δ气温,δ药温,δ海拔,δ其他进行距离修正:
2.2 炮口水平面曲线拟合
弹丸水平向偏移的影响因素主要有横风、方向散布、车体相对于弹丸的横向速度v横,读取射表得到横向偏移密位角θ横、横风修正角α与方位向散布值δ横、飞行时间T,累加方向散布与横向速度vz,拟合投影曲线为:
2.3 射击面曲线拟合
在实际飞行过程中,弹丸受到摩擦、涡流与波动阻力等影响,轨迹呈现“前缓后曲”形状,将外弹道分为升弧段与降弧段,拟合射击投影面曲线时,采用旋转坐标系的方法,设旋转前x1oy1坐标系中曲线函数为:
从射表中读取初始射角、弹道高与坠落角数据:
沿原点顺时针旋转β角并解算参数a、h、k的值:
式中:O—射出点,火药对弹丸作用力为零的点,为了便于计算分析,把O点取在炮口横截面的中心处;旋转角β,射角θ0,最大弹道高度k,落角δ0,修正后射程d,水平距离x,铅垂距离y,在xoy坐标系中,外弹道拟合函数为:
3 系统搭建与模型建立
3.1 系统搭建
模型验证是确定模型准确性的唯一方法[9],通过仿真系统检验拟合外弹道可行性,从功能上主要分为两大部分:仿真帧循环与图形初始化,帧循环的主要任务为刷新图形。
系统实时性要求仿真周期不超过10ms,因此外弹道函数处于系统帧循环功能中,当获取相应的外部环境变量后,系统刷新位置数据并赋予炮弹坐标,同时帧循环中还包括摄像机角度、位置信息与姿态等实体属性;图形初始化的主要任务是创建基础图形环境,加入地形、地物等图形要素,其中的图形环境模块设定相应光源与地形,图形要素模块提供与真实对象相似的外形、音效、场景。
3.2 模型建立
3.2.1 射击模型
射击仿真系统中实体模型主要为坦克车体与炮弹,应用3D Studio Max建模具有模型美观逼真、易于改变视角等诸多优势[10],不仅便于观察内部构造,而且能够分别设置炮管角度与瞄准镜摄像机位置,建模时采取分部件设计方法,依照实体尺寸建模,将各部件装配为一体,使用贴图与渲染功能展现材质与外挂视觉,建立的车体与炮弹模型,如图2所示。

图2 射击模型Fig.2 Shooting Model
3.2.2 射击场景模型
场景环境是仿真中必不可少的因素之一,直接影响受训人员的视觉体验,关系操作感受真实与否,因此为尽可能还原射击场景,应用真实地形的DEM数字高程模型,Global Mapper加载地形文件获取高程数据灰度图,Adobe Photoshop 软件进行画布大小调整,在Unity3D提供的Terrain工具模块中创建地形,设置相应深度与高度,最后地貌依据真实地形纹理数据覆盖,仿真系统中所搭建的部分地形场景,如图3所示。

图3 射击地形场景Fig.3 The Scene of Shooting Terrain
4 实验与结果分析
射击仿真实验验证该仿真方法的可行性,设定环境要素横风值为10km/h、海拔为100m、气温为25℃、空气密度为1.225kg/m3、天气为晴、目标距离为2000m等初始值,搜索目标并选择工作方式,瞄准场景中装甲目标,由拟合函数计算射击此环境中目标炮管与弹丸射击角度应为14.25mil。
当采用0.3mil[11]射击门时,2000m 的距离命中最大误差为0.628m,已能保证较高命中精度,为使实验具有更高仿真性能,采用0.2×0.2mil 的门限值,飞行距离为1100m 时状态与飞行时间1.59s命中目标时的粒子系统爆炸效果,如图4所示。

图4 飞行与爆炸效果Fig.4 The Effects of Flight and Explosion
由于仿真系统中显示的为弹丸整体轨迹,为使拟合外弹道函数结果更加直观,将所得的弹道数据绘制为图表形式展示,不同风速下横向偏移量与飞行距离之间关系曲线,如图5所示。射击面飞行高度与射击距离之间关系,如图6所示。
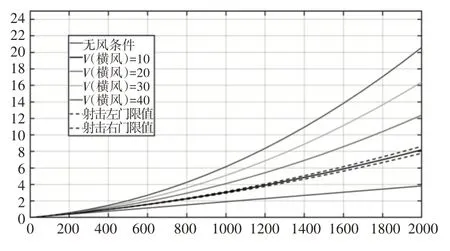
图5 横向偏移与飞行距离曲线Fig.5 The Curve of Lateral Offset and Flight Distance

图6 飞行高度与距离曲线Fig.6 The Curve of Flight Altitude and Distance
拟合两投影面曲线得到的三维弹道图,如图7所示。从这三张图中可以直观看出炮弹的飞行外弹道参数与飞行距离之间关系,当横风速度10km/h时外弹道上部分计算数据,从表格中可以准确地看出偏移量、飞行高度在两个投影面随射击距离的变化值,如表1所示。
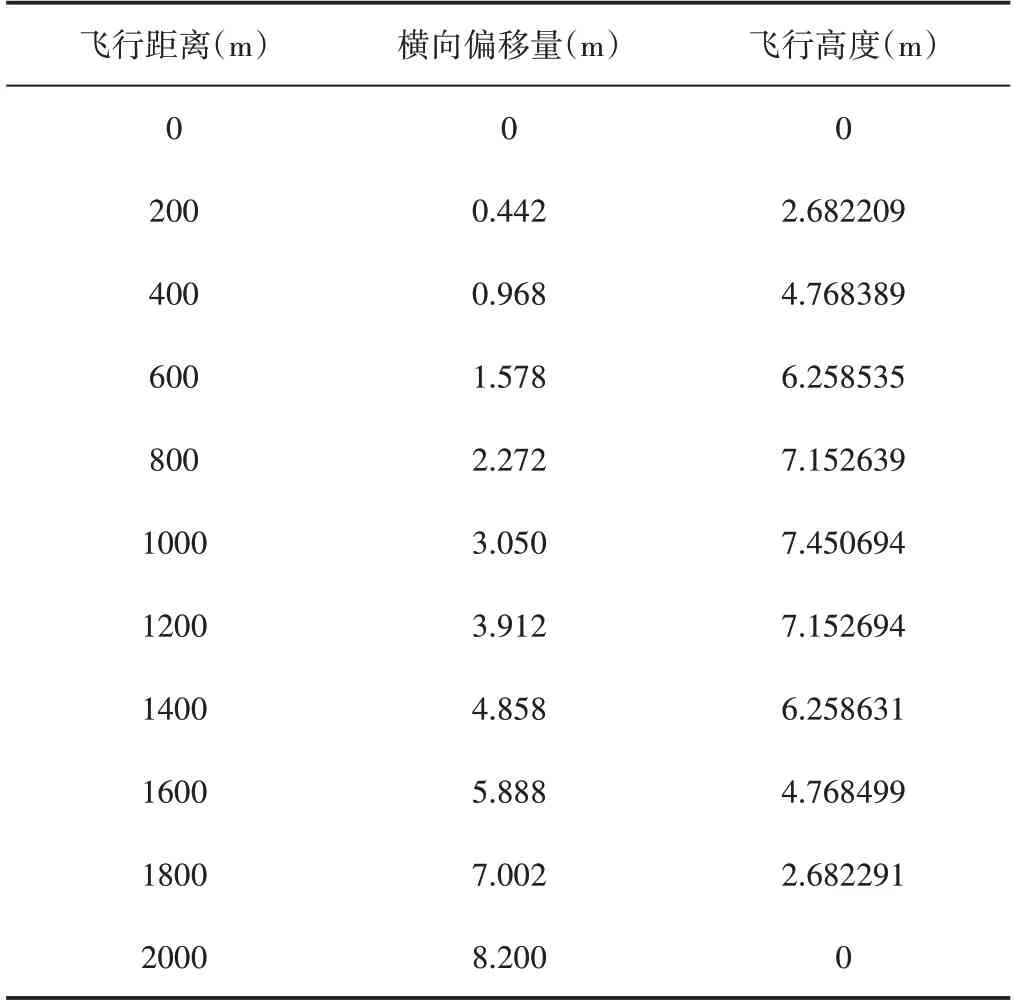
表1 仿真计算结果Tab.1 Simulation Results

图7 外弹道三维曲线Fig.7 Three−Dimensional Curve of Exterior Ballistic
通过系统射击实验结合计算数据可以看出:应用此数学模型结合0.2mil射击门能够准确命中目标,方位向最大误差为0.93m,射击距离最大误差为1.163m,落点位置趋于散布中心,满足系统的可行性要求。
本实验以不同风速0km/h、10km/h、20km/h、30km/h、40km/h为例进行实验,其他环境影响要素同理,在2000m的射击距离时,横向偏移差值分别为4.178m、8.159m 与12.338m,与无风标准气象比较,风速为10km/h 时落点位置最大误差为4.356m,对比射表散布值误差小于5%,此误差在空气环境中不可省略,更能体现真实外弹道特性;从图8观察射击面“前缓后曲”并不明显,这是由于:
(1)射表数据对环境诸元的修正量以数值大小划分等级,在进行距离修正时,采用差值法查取修正量存在一定误差;
(2)实际外弹道极其复杂,影响飞行因素较多,横风、药温、海拔、气温、散布等均为无规律变化,目前对各个偏差量相互交叉作用[12]的研究还不充分,所以在拟合曲线时进行了合理的假设取值与模型简化;
(3)受弹型系数等因素影响,射击实验的选定弹种轨迹较为平缓。
5 结论
通过仿真系统射击试验与弹道数据对比验证,基于射表数据结合环境参数修正量拟合出的数学模型应用在射击仿真系统中具有较高的准确性与实用性,在这里只进行了穿甲弹与改变不同横风值的射击训练实验,其他已知射表数据弹种同样可以应用此数学模型拟合,能够较为精确地描述炮弹外弹道,同时可以用于教学与外弹道研发活动中,对其进一步研究与射击仿真训练系统的优化具有一定的参考价值。

