事件触发机制下多导弹固定时间编队控制
顾镇镇,王旭刚,王中原,华思雨
(南京理工大学能源与动力工程学院,南京 210094)
0 引 言
多导弹编队协同作战是实现分布式作战“兵力分散,火力集中”理念的一种重要手段。发射自不同平台的导弹,通过通信网络相互连结,导弹之间相互支援和协调,协同编队飞行,能够显著提高导弹的目标搜索识别能力,战场态势构建能力,电子干扰对抗能力和突防能力,实现对具有严密防空反导系统的敌方高价值军事目标的打击[1]。
导弹编队协同控制是指在弹群飞行的过程中,使弹群成员之间保持一定的空间位置关系,研究内容包括编队队形的形成、保持和变换等。根据弹间信息交流形式的不同,编队控制系统可以分为分散式、集中式和分布式三种类型。其中分布式的编队控制方法相较于传统的分散式和集中式的控制方法,具有计算速度快、控制方法灵活、可靠性高、鲁棒性强等优点[2]。采用分布式的编队控制方法,可以使导弹在只获取相邻导弹的位置、速度信息的情况下实现编队飞行,并且在损失部分成员时,仍然能够继续执行任务。常用来实现分布式编队控制的策略有领航者-跟随者策略、基于行为策略和虚拟结构策略等,这些控制策略均可以在以图论为基础的多智能体一致性理论中得到统一[3]。本文将在领航者-跟随者策略框架下,基于多智能体一致性理论进行分布式导弹编队控制器的设计。
一致性理论在计算机科学领域有着悠久的历史,自从Fiedler[4]在1973年将代数图论工具引入一致性理论后,一致性理论吸引了大量学者的关注,并在无人作战、深空探测、智能电网等领域有着广泛的应用。对于多智能体一致性问题的研究可以分类为三个方面:第一个方面是针对多智能体系统模型的研究,包括一阶、二阶和高阶系统,线性和非线性系统,连续和离散系统等;第二个方面是对于多智能体通信网络的研究,包括有向/无向通信拓扑,固定/切换通信拓扑,无时延/有时延通信等;第三个方面是对于一致性算法收敛速度的研究。收敛速度是评价一致性算法性能的重要指标,目前大多数关于多智能体一致性理论的研究成果是基于渐近收敛一致性的[5-6],这意味着一致性的达成需要无限长的时间。虽然渐近收敛一致性在收敛时间方面不占优势,但对其进行研究仍是必要的,其它严格时间收敛一致性理论大多是由渐近收敛一致性理论发展而来的。
对于收敛速度的追求促进了有限时间一致性理论的发展。与渐近时间一致性结果相比,有限时间一致性具有更好的动态特性,更高的精度和更快的收敛速度[7-8]。有限时间一致性理论被广泛应用于工程实践中,然而由于其一致性达成时间高度依赖于系统状态的初始值,因此,当系统状态的初始值较大或者无法预先获得时,有限时间一致性算法并不适用[9-10]。
为了解除上述限制,在有限时间一致性算法的基础上,开发了固定时间一致性算法,在该算法的作用下,多智能体系统达到稳定的时间与其初始状态无关。目前,已经有大量的研究成果证明了固定时间一致性理论在多智能体系统中的有效性。在文献[11]和文献[12]中,提出了固定时间一致性跟踪算法,并将其成功应用于多机器人的编队。文献[13-14]分别将固定时间控制算法应用于二阶和高阶的动力学系统中。由于实际的系统都是非线性的,因此对非线性多智能体系统的固定时间一致性协议进行分析是自然的,文献[15]提出一种自适应固定时间控制协议,解决了一类具有不对称输出约束要求的多输入多输出非线性系统的跟踪一致性问题。文献[16]通过设计状态观测器,解决了没有速度测量的非线性二阶多智能体系统的固定时间跟踪一致性问题。文献[17]研究了具有输入延迟的二阶多智能体系统的跟踪一致性问题,通过归约变换将延迟误差系统转化为无时延的二阶系统,提出了一种新的非奇异终端滑模协议来实现固定时间一致性。在一致性控制算法中,智能体所需的初始控制输入一般很大,然后就快速衰减,针对该问题,Ning等[18]基于时基生成器开发了一种新的固定时间一致性框架,显著降低了控制输入的初始幅度大小。
在上述的这些工作中,多智能体一致性的达成都依赖于“连续通信”这一假设,这种假设要求多智能体系统必须有强大的计算资源和理想的通信环境支持。在实际的多智能体系统中,智能体一般依靠自身内部电源供电,处理器的计算能力和通信带宽都是有限的,频繁的通信会带来延迟和丢包并消耗大量的计算资源,这将导致控制系统的不稳定并缩短执行任务的可用时间。此外,当系统运行在稳定状态并且没有干扰时,相邻智能体间的持续通信是不必要的。基于事件触发机制的一致性算法,为每个智能体的测量误差设定了一个阈值,只有当智能体的状态误差达到阈值时,才会与相邻智能体进行通信并进行控制信号的更新,有效解决了有限的计算资源和通信带宽带来的问题。Liu等[19]研究了无向通信拓扑条件下,一阶多智能体系统基于事件触发机制的固定时间一致性,给出了集中式和分布式两种事件触发策略,其中每个智能体只在自身触发时刻才与系统进行通信并更新自身的控制输入,相比文献[20]中一个智能体触发,所有智能体都要更新控制输入的情况,显著降低了事件触发的次数。Zhou等[21]提出了基于智能体自身状态误差的事件触发函数,计算事件触发函数时仅需要智能体自身的状态信息和相邻智能体触发时刻的状态信息,有效解决了无向通信拓扑条件下,二阶多智能体的固定时间一致性问题。但值得注意的是,绝大多数关于固定时间和事件触发控制的一致性算法仅适用于无领导者的情况,对跟踪一致性的研究成果极少。在文献[22]提出的算法中,多智能体的一致性达成之后,阈值函数接近于零,由于领导者的运动状态是不断变化的,所以测量误差并不为零,无法排除Zeno行为。Guo等[23]对有向通信拓扑下,基于事件触发的二阶多智能体的领导跟随固定时间一致性进行了研究,然而其提出的事件触发函数需要获取相邻智能体的实时运动状态,违背了事件触发函数设计的初衷。
综上所述,由于有向拓扑下Laplacian矩阵的不对称性和事件触发通信引入的误差项对系统稳定性分析带来的困难,目前鲜有适用于有向通信拓扑,带有领导者的基于个体自身状态触发事件的固定时间一致性协议来满足本文对于多导弹编队控制的需要。本文对该一致性问题进行了研究,并将其成功应用于多导弹编队控制,主要贡献有以下两个方面:
1)在有向通信拓扑下为弹群设计了固定时间编队控制协议。保证了初始位置差距较大、速度较快的导弹成员在较短的时间内达到编队飞行所需的运动状态,并跟随领弹进行机动。
2)在有向通信拓扑下设计了适用于领导跟随一致性的从弹自身状态事件触发函数。从弹事件触发函数的计算仅需要获取相邻从弹的触发时刻状态和领弹的飞行状态,不需要获取相邻从弹实时状态,降低了从弹通信网络中的信息传递所需带宽,节省了网络和计算资源。
有向通信拓扑是无向通信拓扑的一种特殊情况,其优势是可以减小弹间通信所需的带宽,降低对通信系统的要求。但是,有向通信拓扑的Laplacian矩阵的不对称性,给系统的稳定性分析带来了挑战。
本文的剩余部分安排如下,在第1节中给出了文中常用的符号表示、代数图论相关知识和证明所需的一些引理。第2节首先对本文研究的作战场景进行描述,然后用微分几何线性化方法将导弹运动模型精确线性化,并给出了多导弹编队的固定时间一致性判定条件。在第3节中为导弹设计了固定时间编队控制协议和基于事件触发机制的固定时间编队控制器。第4节通过数值模拟校验了两种算法的有效性。在第5节中给出本文的结论。
1 预备知识
1.1 符号
1.2 代数图论
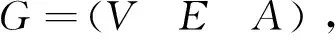
代数图论是研究图的结构与图的矩阵表示之间关系的理论,代数图论被用在多智能体系统中最重要的两个概念是邻接矩阵和Laplacian矩阵。图的邻接矩阵A=[aij]∈RN×N,其对角元素aii=0,当图的两个顶点之间的联系(vj,vi)∈E时,aij>0,当(vj,vi)∉E时,aij=0。对于有向图来说,入度矩阵定义为Din=diag(di,in)∈RN×N,di,in=∑j∈Niaij,出度矩阵定义为Dout=diag(di,out)∈RN×N,di,out=∑j∈Fiaji。图G的Laplacian矩阵可以表示为L=[lij]=Din-A,其中lii=∑j∈Niaij,并且lij=-aij,∀i≠j。
1.3 相关引理
引理1[1].此引理给出仿射非线性系统能够用微分几何法精确线性化的充要条件。
微分几何法的适用对象是如下仿射非线性系统。
(1)
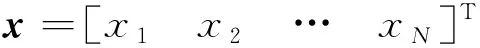
对于该非线性系统,如果系统初始状态x=x0,并且G(x)是列满秩矩阵,则该非线性系统能进行反馈线性化的充要条件是
1)Gi(0≤i≤N-1)是对合的,并且在初始状态x0的邻域内维度不变。
2)GN-1是N维的。
在上述判定条件中,Gi的定义为
(2)
式中:
ri=card(mj|mj≥i,j≥0),
mj=rankGj-rankGj-1,j=1,2,…,N-1,
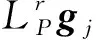
引理2[19].系统固定时间稳定性理论。
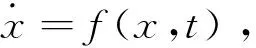
1)V(x)=0⟺x=0。
2)D+V(x)≤-aVp(x)+bVq(x)。
式中:a,b,p,q为正常数,p∈(0,1),q∈(1,+∞)。则系统可以实现全局固定时间的稳定,且稳定时间T满足
(3)
引理3[23].a,b∈R+,r(x,y)>0是实值函数,则有
(4)
2 多导弹编队控制问题描述
2.1 作战场景及编队控制策略描述
本文研究的作战场景是使用导弹武器对具有一定防空力量的敌方军事目标(如敌方舰艇编队)进行打击,假设已获取的信息只有敌方目标的粗略位置。作战过程如图1所示,从多个平台发射的多枚导弹在预定的空域内集结,弹间形成稳定的通信链路并以高低弹道编队队形向目标抵近,一枚导弹在高空飞行,搜索目标,其余导弹在低空跟随,以穿透目标的远程和中程防空网络。在传感器发现目标所在位置后,进行协同制导律的交接,实现多导弹对目标的同时打击,在短时间内对目标的近程防空系统造成巨大压力,使其出现过载而无法全部拦截。本文对上述弹群协同作战过程中的编队飞行控制问题进行研究,并采用领航者-跟随者编队控制策略来实现具备侦察-打击一体化功能的弹群编队控制。
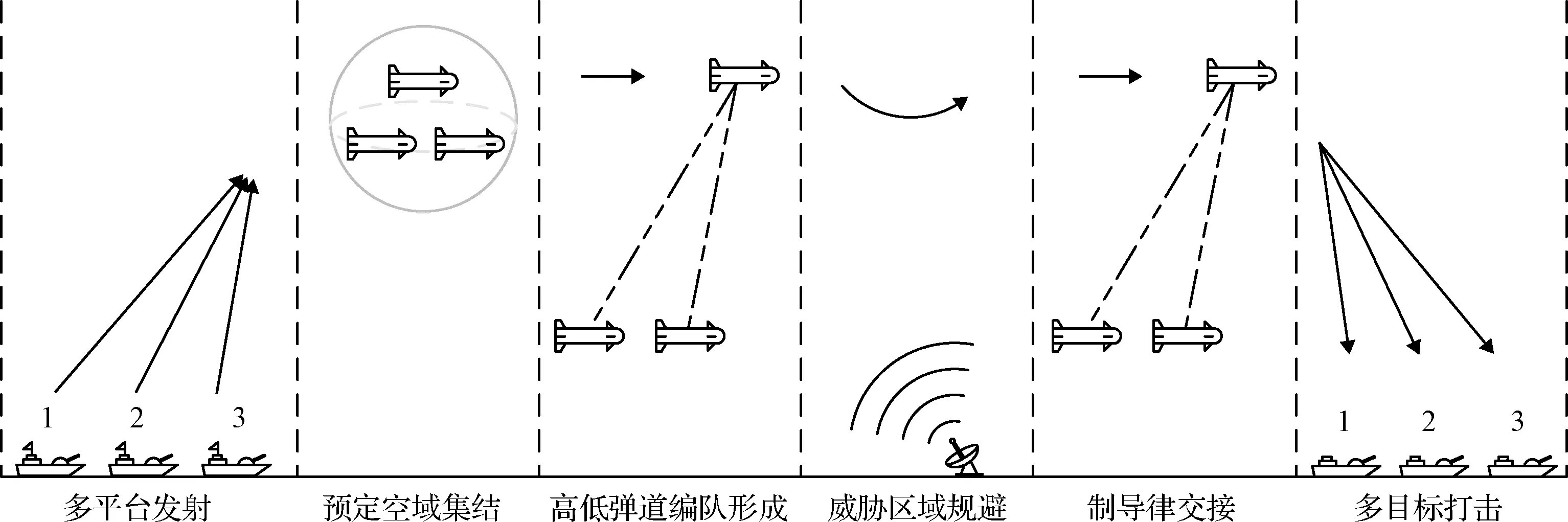
图1 弹群协同编队作战示意图Fig.1 Schematic diagram of missile-group cooperative operation
2.2 多导弹编队模型及基于微分几何理论的精确线性化
本节考虑由一枚领弹和N枚从弹组成的群体系统。首先对单枚导弹进行运动学和动力学建模,然后基于微分几何理论对导弹模型进行精确反馈线性化,将描述导弹运动的非线性模型变换为方便控制的线性模型。由于基于微分几何理论的反馈线性化方法是通过微分同胚进行严格的状态变换来实现线性化的,在变换的过程中没有忽略任何高阶非线性项,所以从理论上来说该方法不会引入新的线性化误差。
在编队飞行过程中,导弹的姿态变化相较于轨迹变化要小的多,基于“瞬时平衡假设”,可以将导弹作为一个可操纵质点来研究。为了便于编队控制系统的设计,将导弹的过载作为编队控制的输入量,针对单枚导弹,建立运动方程组如下式所示。
(5)
式中:i={1,2,…,N}∪{l},其中i=1,2,…,N表示编队中的N枚从弹,i=l表示领弹;Vi,θi和ψVi分别表示第i枚导弹的速度、弹道倾角和弹道偏角;nxi,nyi和nzi分别表示第i枚导弹的过载在弹道坐标系o1x1y1z1下的分量;xi,yi和zi表示第i枚导弹在惯性坐标系下的空间位置,g为重力加速度。
下面用微分几何法对上述模型进行反馈线性化。首先选取控制变量和状态变量为ui=[nxinyinzi]T和xi=[xiyiziViθiψVi]T。则导弹的运动方程组(5)可以改写为如下的仿射非线性形式。
(6)
式中:
Kq=diag{g,g/Vi,-g/(Vicosθi)},
根据引理1,可以验证Gi,i=0,1,…,5是对合的,其维度在系统的初始状态x0的邻域内不变且为6。因此非线性系统(6)满足全状态反馈线性化的充要条件,能够基于微分几何法线性化为可控系统,且可控指数为2。由于可控指数在反馈线性化的过程中是不变的,即存在一个光滑的向量函数
使得
〈dφi,Crj-2〉=0,j≥i
(7)
选取满足上式的光滑向量函数φ(x)和微分同胚τ(x)为
则仿射非线性系统(6)能被精确线性化为如下的可控线性系统
(8)
式中:
Hl和Ml为能控标准型;zi为线性系统的状态变量;vi为虚拟控制输入,与真实控制输入ui的关系为
vi=ο(xi)+π(xi)ui
(9)
式中:
至此,导弹的运动模型通过微分几何方法精确线性化为如下解耦的线性二阶积分形式。
(10)
式中:xi,yi和zi为导弹惯性坐标系中的空间位置;vxi,vyi和vzi分别为导弹三个通道的虚拟控制输入。
接下来可以用二阶多智能体一致性问题的研究方法来解决多导弹编队飞行控制问题。
2.3 多导弹编队的固定时间一致性
本文的主要目的之一是基于领-从弹编队策略设计一个编队控制器,使弹群中所有的导弹在较短的时间内收敛到所需的编队队形,并且在领弹进行机动的情况下,编队的队形能够保持稳定。领-从弹编队结构如图2所示。
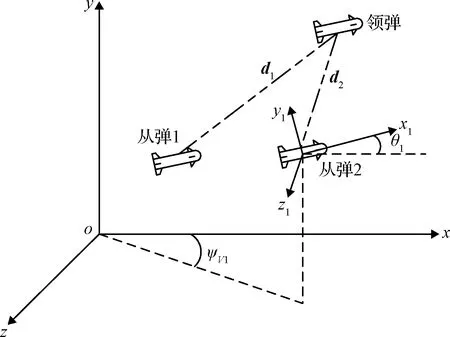
图2 领弹-从弹编队结构示意图Fig.2 Schematic diagram of leader-follower missile formation
(11)
用向量di表示第i枚从弹与领弹间的期望相对位置,从弹的期望位置和速度跟踪误差可以表示为
(12)
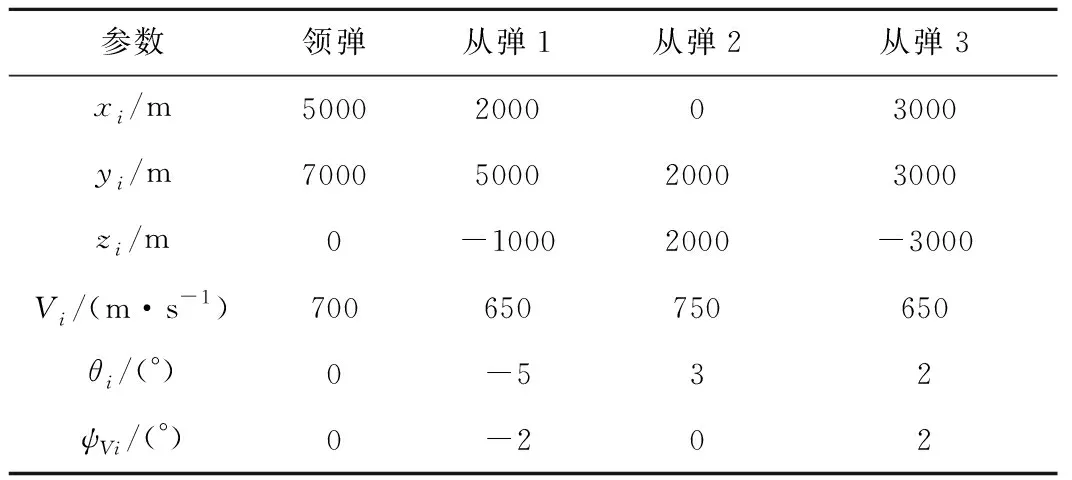
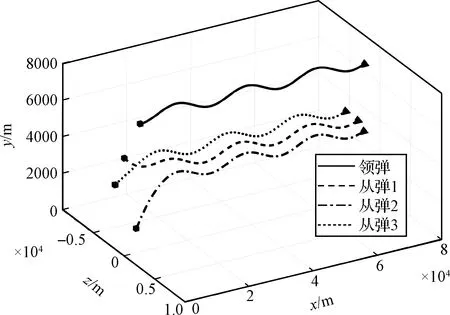
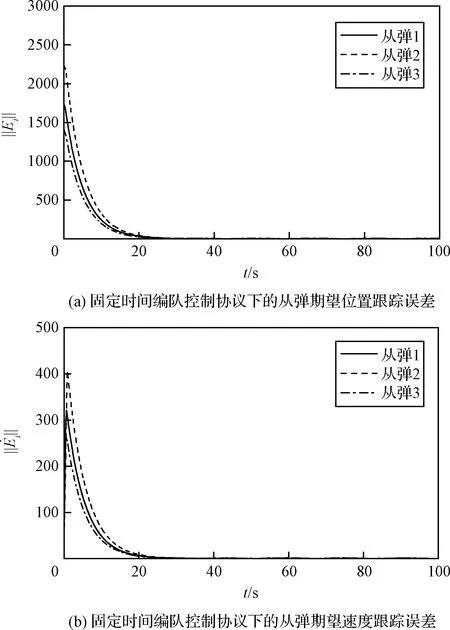
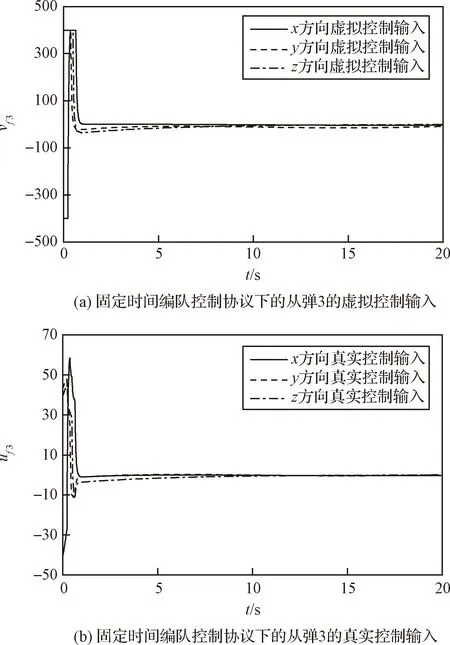
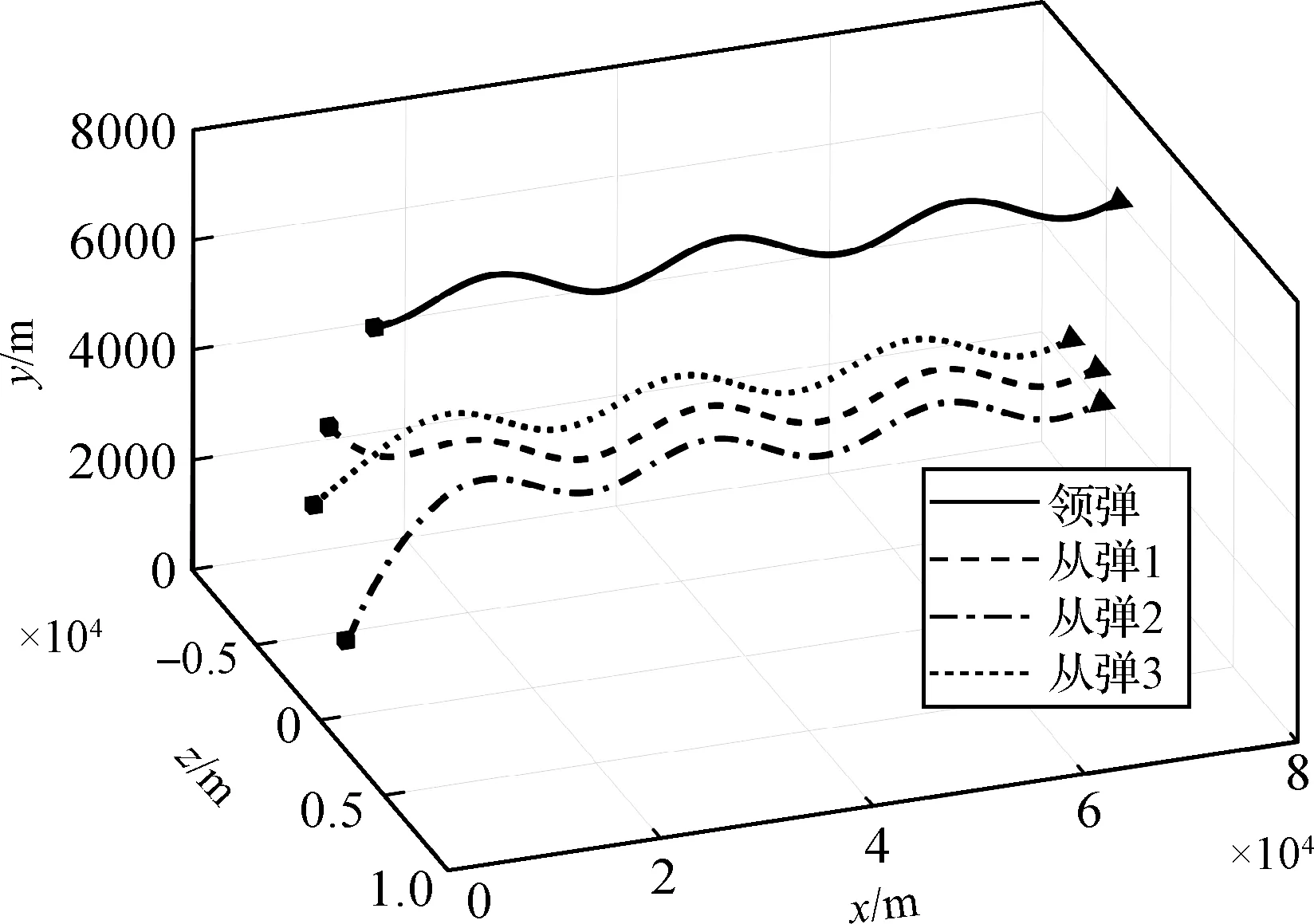
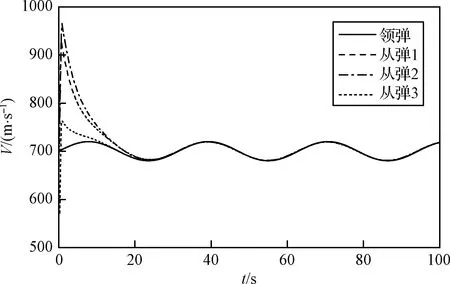
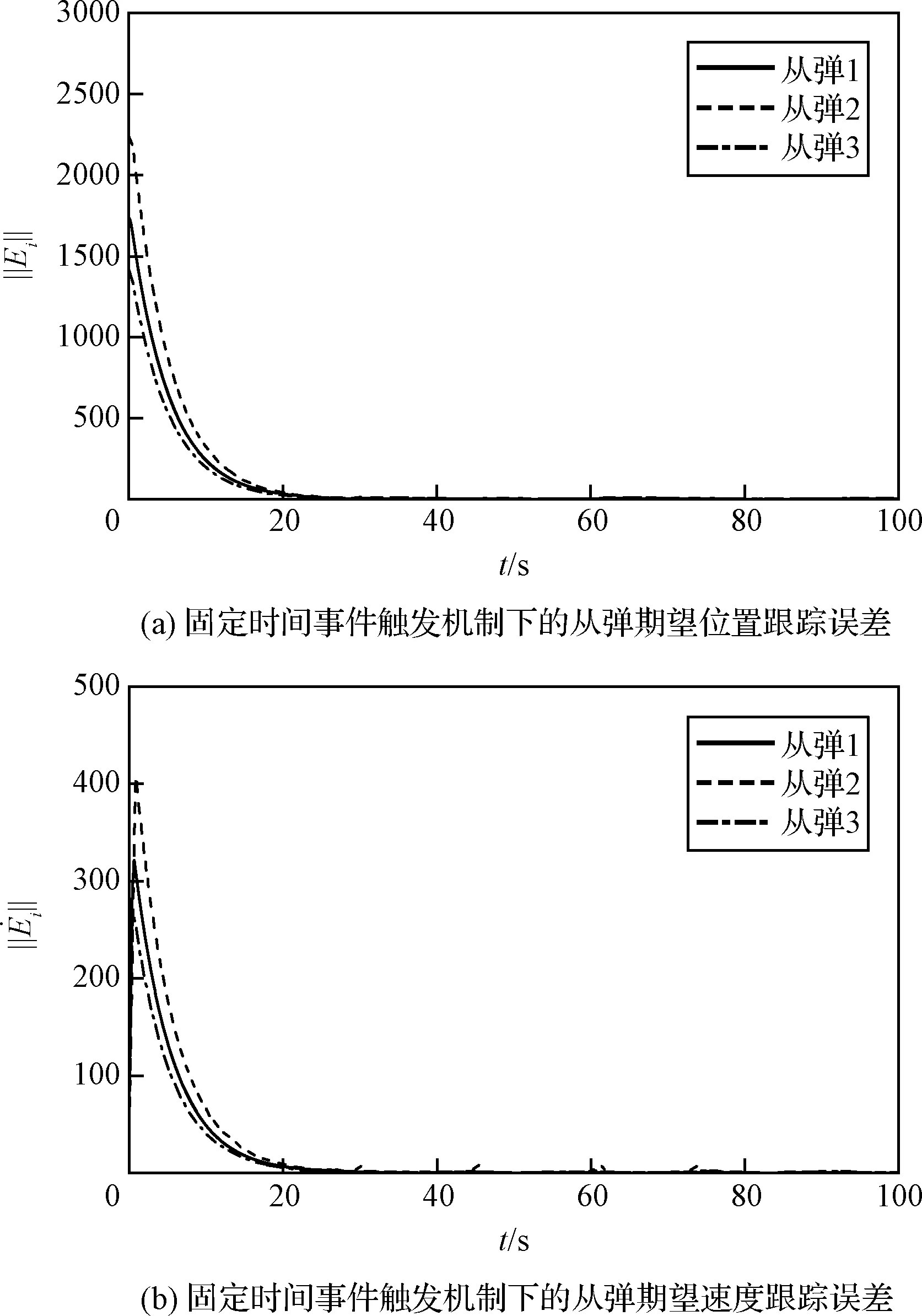
如果在任意的初始条件下,编队控制器都能使群体系统在时间T (13) 和 (14) 则称群体系统在固定时间内实现了稳定编队。 编队的实际收敛时间T 为了解决领-从弹编队结构中,从弹对领弹的协同跟踪控制问题,本节首先基于群体系统周期采样数据进行固定时间编队控制协议的设计,保证具有较大飞行速度的导弹群体系统能够在较短时间内达到稳定。然后为了节省通信带宽和弹载计算资源,在固定时间编队控制协议的基础上引入了事件触发机制,进行基于事件触发策略的固定时间编队控制器设计。 为满足多导弹编队对于队形收敛时间的严格要求,本节基于多智能体一致性理论,对弹群进行固定时间编队控制协议的设计。由于线性化后的导弹模型具有解耦的线性二阶积分形式,故导弹x,y,z三个控制通道是相互独立的,可以分别进行控制协议的设计。本节以x通道为例,给出其固定时间编队控制协议。 考虑群体系统的通信结构为有向拓扑,并且领弹是全局可达的,其运动状态独立。第i枚从弹的编队控制协议设计为 vfxi=hi(t)+sig[hi(t)]a+sig[hi(t)]b+vlx (15) 式中: hi(t)=αpi(t)+βqi(t) (16) (17) 在所设计的固定时间编队控制协议中,hi(t)项被设计用来实现编队的渐近稳定性;sig[hi(t)]a和sig[hi(t)]b项被设计用来实现编队的固定时间稳定性;vlx项是为了使群体系统在形成编队队形的同时,跟随领弹的运动轨迹。 则式(17)可以写成如下矩阵的形式。 (18) 对上式进行微分可得 (19) 领-从弹编队系统固定时间一致性问题在此转化为系统(19)的固定时间稳定性问题,给出如下定理。 定理1.当下列条件成立时,在给定的固定时间编队控制协议(15)作用下,系统(19)能在固定时间内收敛到一致,也即多导弹编队能够在固定时间Tmax内收敛到稳定状态。 (20) 式中: μ1为矩阵M+MT的最小特征值。 证.定理1的证明分为三步,首先构建包含变量pi(t)和qi(t)的Lyapunov函数;然后证明固定时间编队控制协议能实现群体系统的渐近稳定性;最后通过构建的Lyapunov函数和其导数的关系,证明该控制协议能实现群体系统的固定时间稳定性。 (21) 式中: 所选取Lyapunov函数V(t)的符号由矩阵Ω决定,当且仅当矩阵Ω正定时,V(t)≥0。由于领弹是全局可达的,所以矩阵M+MT是对称矩阵,且所有特征值均为正的实数,即矩阵M+MT为正定矩阵且能被相似对角化,如下式所示。 Γ(M+MT)Γ-1=Λ (22) 矩阵Ω为实对称矩阵,根据文献[21]中引理3,当且仅当Γdiag(β2μi-α)Γ-1>0时,矩阵Ω正定。从条件(20)可知,该不等式成立,故V(t)≥0。对V(t)进行微分可得 (23) 将式(19)代入上式,可展开为 hTMsig(h)a-hTMsig(h)b (24) 为书写方便,定义m1,m2,m3,m4分别为上式中等号右侧从左到右四项,对这四项进行分析。 (25) (26) (27) 由引理3可得 (28) 联立上述两式,并化简得 (29) 取 (30) 则m3可以表示为 (31) 同理,取 (32) 对m4进行放缩可得 (33) 由于定理1中条件(20)的约束,m1和m2项均不大于0,则式(28)可以放缩为如下的形式。 (34) 在编队的一致性达成之前,有下列不等式成立。 ρT(Θ⊗IN)ρ>0 (35) 取有界闭集U={χ∈R2N:χTχ},可以得到 (36) 因此 (37) 由式(21)得 (38) 式中:λmax(Ω)为矩阵Ω的最大特征值。 根据文献[21]中引理4,式(43)可被改写为如下形式: (39) 将式(38)代入上式并化简可得: (40) 式中: k3=k1(2κ/λmax(Ω))(a+1)/2, k4=k2N(1-b)/2(2κ/λmax(Ω))(b+1)/2。 根据引理2,系统能在固定时间内达到稳定,且稳定时间T与系统的初始状态无关且满足 (41) 同理,可以设计y通道和z通道的控制协议。 上文中的固定时间编队控制协议是基于传统的周期采样控制设计的,编队中的导弹需要连续不断的通信和对自身的控制参数的计算,来达到期望的编队队形。考虑在实际的导弹编队飞行过程中,通信带宽和弹载计算资源的限制,本节在固定时间编队控制协议的基础上,克服有向拓扑下Laplacian矩阵的不对称性和事件触发通信引入的误差项对系统稳定性分析带来的困难,引入事件触发机制对弹群进行编队控制器的设计。针对每个从弹设计基于自身状态误差的事件触发函数,只有当状态误差满足所设定的阈值时,导弹才更新并在弹群中传递自身的状态信息。 同样考虑弹间通信拓扑是有向的,则第i枚从弹的编队控制协议设计为 (42) 式中: (43) (44) 定义从弹i的时变位置误差和速度误差为 (45) 定义位置组合误差和速度组合误差为 (46) 为第i枚从弹设计基于自身状态的触发函数为 (47) 有以下矩阵形式的关系式成立。 (48) 式(43)可以表示为如下的形式。 γp(t)+δq(t) (49) 在控制输入(42)的基础上,对式(18)微分可得 (50) 基于事件触发机制的固定时间一致性问题在此转化为系统(50)的稳定性问题,给出如下定理。 定理2.当下列条件成立时,基于事件触发机制的固定时间编队控制协议能使群体系统(50)在固定时间内收敛到稳定状态。 (51) 式中:σ为矩阵MMT的最大奇异值。 证.定理2的证明分为四步。首先构建包含变量pi(t),qi(t)和时变误差eix,eiv的Lyapunov函数;然后证明在控制协议(42)的作用下,导弹编队能够渐近稳定;接着证明系统的固定时间稳定性;最后证明所设计的事件触发函数排除Zeno行为。Zeno行为是指在有限的时间间隔内,事件函数被无限次的触发。 设计的Lyapunov函数和定理1中相同,可知V(t)≥0,t∈[0,+∞)。对V(t)进行微分可得 (52) 将式(49)和式(50)代入上式并展开可得 δqT)M(γex+δev)-(γpT+δqT) (53) 为书写方便,定义n1,n2,n3,n4分别为上式中等号右端四项,分别对这四项进行分析。 (54) 由事件触发函数(47)可得 (55) 进而有 (56) 即 (57) 利用上述条件对n2进行放缩得 (58) 接下来对n3项进行放缩得 (59) 对上式中等号右端两项分别进行分析,根据文献[21]中引理5可得 (60) 由式(31)可知 (61) 因此 (62) 同理可得 (63) 将n1,n2,n3,n4代入式(53)可得 (64) (65) (66) 将式(66)代入式(65)得 (67) 式中: 由引理2可得,系统能在固定时间内达到稳定,且稳定时间T与系统的初始状态无关: (68) 由于在群体系统的一致性达成以后,领弹继续保持机动,事件触发函数的阈值大于0,Zeno行为不会出现。接下来证明群体系统在达到稳定之前Zeno行为被排除。在群体一致性达成之前有 (69) 定义 (70) 则有 (71) (72) 进而有 (73) (74) (75) 因此在本文所设计的事件触发机制下,群体系统排除Zeno行为,证明完毕。 本节通过数值仿真来校验所设计编队控制算法的有效性和稳定性分析的正确性。考虑由3枚从弹和1枚领弹组成的群体系统,设计弹间通信拓扑及通信链路权重如图3所示。弹间的通信拓扑被设计为有向的,相较于无向通信拓扑而言,可以更有效地节约通信资源。 图3 弹间通信拓扑图Fig.3 Communication topology of the missile formation 图G的Laplacian矩阵为 (76) 领弹的邻接矩阵为 (77) 为校验领弹进行机动时,从弹对领弹的跟踪情况和编队队形的保持情况,设计领弹的运动状态如下。 (78) 领弹按照上式进行机动时,从弹在x方向需要跟踪一个较大的速度,在y方向跟踪一个较小的速度,而在z方向上跟踪的速度为0。由于从弹的三个控制通道是分别进行设计的,因此在领弹按照上式机动的情况下,可以更好的校验本文提出的固定时间编队控制算法对不同大小速度的跟踪性能。从弹和领弹的初始状态信息由表1给出。 表1 导弹编队初始状态Table 1 Initial state of the missile formation 根据本文研究的作战场景,设计适配侦察-打击一体化功能的高低弹道编队,导弹编队的队形在惯性坐标系中给出,从弹与领弹间的期望相对位置为 (79) 固定时间编队控制协议(15)中的α,β为要设计的反馈增益,用于调整弹群的位置和速度组合状态对于编队状态的影响。α,β具有非常灵活的调整范围,在保持α不变的情况下,增加β将增加群体系统达到稳定的时间,同时减小导弹所需要的控制输入。在β保持不变的情况下,增加α将提高编队收敛的速度,同时导弹所需要的控制输入也更大。a∈(0,1)和b∈(1,+∞)也是要设计的控制参数,减小a会使编队的收敛速度加快,但是当a∈(0,0.5)时,继续减小a,编队的收敛速度提升的并不明显,因此在数值仿真中取a∈(0.5,0.9)。b的选择一般不大于2,过大的b会导致所需初始控制输入的快速增大。 基于事件触发机制的固定时间编队控制算法(42)中控制参数的设计同固定时间算法(15)类似,事件触发函数(47)中的m要在条件(51)允许的范围内设计的尽可能大,来避免事件被频繁触发。 结合上述分析,在本节的数值模拟仿真中,取α=γ=2,β=δ=10,a=c=0.8,b=d=1.2,m=0.12,仿真时间t=100 s,采样间隔为0.001 s。 图4~9给出了在固定时间编队控制协议作用下导弹编队各成员运动参数的变化情况。3枚从弹跟随1枚领弹编队飞行的三维空间运动轨迹如图4所示,可以看出,从弹由给定的初始位置逐渐收敛到编队队形中的期望位置,并跟随领弹进行机动。 图4 固定时间编队控制协议下的导弹飞行轨迹Fig.4 Missles’ trajectory based on fixed-time formation algorithm 图5给出了导弹在x,y,z三个方向上的速度分量变化情况,可以看出,在t=24 s时,从弹的三个方向速度分量同时跟踪上领弹的速度分量,又由于在t=0时刻,领弹和从弹在x,y,z轴的速度分量大小是不一样的,由此可以验证固定时间编队控制算法的收敛时间与群体系统的初始状态无关。 图6给出了导弹总的速度变化情况,可以看出,在导弹编队形成的过程中,从弹1的速度最大达到了960 m/s,其它从弹的速度也都存在短暂的上升。从弹速度的短暂上升主要是由于一致性算法的特性和对编队稳定时间的要求造成的,可以通过调整控制参数,增大编队达到稳定的时间,来减小从弹在达到编队稳定过程中需要的最大速度。 图6 固定时间编队控制协议下的导弹速度变化Fig. 6 Missles’ velocity based on fixed-time formation algorithm 图7给出了从弹的期望位置跟踪误差和速度跟踪误差,二者随着时间的增加逐渐减小,并且都在t=24 s时收敛到0,说明此时编队的队形已经形成,并在此后的时刻保持稳定。 图7 固定时间编队控制协议下的从弹跟踪误差Fig.7 Followers’ tracking error based on fixed-time formation algorithm 以从弹3为例,给出其在编队过程中x,y,z三个通道的虚拟控制输入和真实控制输入如图8所示。考虑弹载执行机构的执行能力,为虚拟控制输入设定了|vf|≤400的阈值,从而将从弹的三个控制通道所需过载均控制在60以内。 图8 固定时间编队控制协议下的从弹3的控制输入Fig.8 Control input for the follower 3# based on fixed-time formation algorithm 图9~12给出了弹间通信结构为图3所示的有向权重拓扑条件时,在基于事件触发机制的固定时间编队算法(42)作用下,导弹编队中各成员运动参数的变化情况。 图9 固定时间事件触发机制下的导弹飞行轨迹Fig.9 Missles’ trajectory based on fixed-time event-triggered formation algorithm 图10 固定时间事件触发机制下的导弹速度变化Fig. 10 Missles’ velocity based on fixed-time event-triggered formation algorithm 图11 固定时间事件触发机制下的从弹跟踪误差Fig.11 Followers’ tracking error based on fixed-time event-triggered formation algorithm 图12 固定时间事件触发机制下的从弹3的事件触发时刻Fig.12 Event time of follower 3 based on fixed-time event-triggered formation algorithm 从图9~11可以看出,在基于事件触发机制的固定时间编队控制算法的作用下,从弹同样实现了对期望位置和速度的跟踪,并在t=24 s时编队收敛到期望队形。如图11所示,由于事件触发函数阈值的存在,在一致性达成之后,从弹的期望位置跟踪误差和期望速度跟踪误差并不为零,可以通过对事件触发函数阈值的设置,来调整从弹的期望位置跟踪误差和期望速度跟踪误差,进而满足编队设计的精度需求。 以从弹3为例,其三个控制通道的事件触发时刻分布如图12所示。由于从弹在x轴方向跟踪的位置和速度状态变化最大,所以测量误差最频繁的达到所设定的阈值,导致事件的触发;在y轴方向跟踪的位置和速度状态变化稍小,所以其事件触发次数显著降低;由于领弹在z轴方向不做机动,所以从弹在z轴方向跟踪的位置是固定值,速度是零,当z轴方向的一致性达成以后,事件便不再触发。由此可以得出结论,基于事件触发机制的编队控制算法可以有效的节省计算资源和通信带宽,事件触发函数的触发次数与编队的机动情况相关。 对固定时间编队控制协议和基于事件触发机制的固定时间编队控制协议仿真实验结果从以下三个方面进行对比分析。 1) 编队收敛速度。通过合理设置参数,固定时间编队控制协议可以保证具有较大初始状态的弹群系统在24 s内收敛到稳定,在引入事件触发机制后,编队的收敛时间仍为24 s,可见事件触发机制的引入并未对编队的收敛速度产生影响。 2) 编队飞行误差。在固定时间编队控制协议作用下,导弹编队队形收敛到一致后,从弹的期望位置跟踪误差和期望速度跟踪误差都为0,在引入事件触发机制后,由于事件触发函数阈值的存在,从弹的期望位置跟踪误差和期望速度跟踪误差均不为0,该误差可以通过相关参数的设置来进行调节。 3) 编队通信频率。固定时间编队控制协议是基于周期采样控制设计的,在本文的仿真实验中采样间隔设置为0.001 s,而引入事件触发机制后,只有在事件触发时刻才会触发从弹间通信,从弹的事件触发时刻如图12所示,有效降低了从弹间通信的频率。 综上所述,在固定时间编队控制协议的基础上引入事件触发机制,可以在保证弹群系统以较快速度达到稳定的前提下,有效的节约通信带宽和弹载计算资源。 本文结合实际作战场景,对多导弹协同编队控制问题进行了研究。主要结论如下: 1) 本文设计的固定时间一致性编队控制协议,能够保证初始位置差距较大、速度较快的导弹编队在较短的时间内收敛到稳定状态,并跟随领弹进行机动。 2) 本文设计的基于从弹自身状态触发事件的编队控制器,能有效减少弹群编队所需的通信带宽和弹载计算资源。 3) 本文所设计的编队控制协议适用于弹间通信是有向拓扑的情况。相较于无向通信,有向通信对于复杂的战场环境具有更强的适应性,并且可以降低对弹载通信设备的要求。3 事件触发机制下多导弹固定时间编队控制器设计
3.1 固定时间编队控制协议
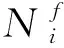

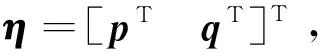


3.2 事件触发机制下固定时间编队控制器设计
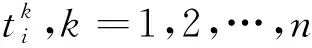

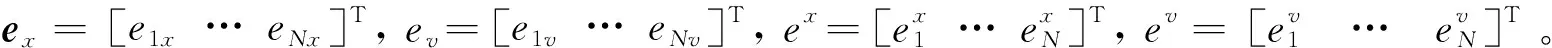

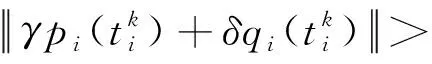
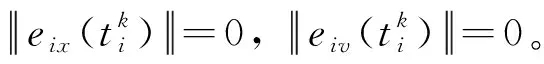
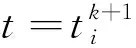
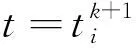
4 多导弹编队控制系统仿真





5 结 论

