火箭发动机七机并联机架预应力模态分析及优化

李 斌，吕 军，曾耀祥，王 檑，刘 晖，张 盛，崔 苗

(1. 大连理工大学航空航天学院，大连 116024； 2. 工业装备结构分析国家重点实验室，大连 116024；3. 辽宁省空天飞行器前沿技术重点实验室，大连 116024； 4. 中国运载火箭技术研究院，北京 100076； 5. 大连理工大学工程力学系，大连 116024)

0 引 言

为能够保障更大规模的载人航天活动以及开展载人深空探测任务，需探索新型载人运载火箭。目前正在论证的新型载人运载火箭芯一级采用5 m直径的模块，安装七台新型液氧煤油发动机[1]。火箭发动机机架作为火箭发射时的主要承力结构，尤其是在具有大推力的运载火箭上，发动机工作产生的振动问题不容忽视，需进行深入研究。在火箭起飞瞬间，较大的加速度和结构自身重力会使机架结构承受很大的预应力载荷，势必会对机架的动力学特性产生重要影响。因此，有必要开展多台并联火箭发动机机架结构在预应力载荷作用下的非线性动力学行为分析研究。

对于一些轻型运载火箭发动机机架的力学响应和设计优化问题，国内外学者从静态、动态响应等方面开展了研究[2-4]。Yoo等[5]研究了75吨级液体火箭发动机的静态和动态结构响应，分析了静态载荷对应力分布和结构自由振动的影响。汤波等[6]对我国新一代中型运载火箭分析了悬挂工装对箭体模态的影响。另有一些学者[7-9]通过使用加筋、材料更换、参数化建模等方法优化单或双台发动机机架，提高机架动静强度并对结构有效减重。上述研究侧重于单机或双机火箭发动机机架的计算和优化，且大多仅以结构线性动力学参数作为考量因素。

新型载人运载火箭芯一级通常并联安装多台发动机，每台发动机与箭体之间通过独立的小机架结构进行连接，相比单、双机问题，此类机架的传力情况更复杂，因此并联多台火箭发动机机架的设计具有新的挑战性[10-11]。目前国外学者开展了SpaceX研发的猎鹰-9的八爪式推力架，以及土星-5运载火箭十字横梁结构的设计与分析[12-14]，通过试验验证，两种机架结构在动静上都能满足多机并联火箭的强度要求。另一方面，王建民等[15]总结了捆绑火箭的模态分布特点，给出了捆绑火箭横、纵、扭模态互相耦合的特征。黄道琼等[16]开展了四机并联发动机机架低频模态分析研究，指出了轴向运动较大的各阶频率。杜飞平等[17]基于子结构试验建模综合技术，开展了四机并联液体火箭发动机结构动力学研究。上述研究中忽略了实际工况中预应力载荷的影响，且已有相关研究大多都针对于四机及其以下并联火箭或捆绑火箭，对于五机及其以上并联火箭发动机推力传递结构的动力学特性研究还处在起步阶段。如何轻质高效地实现并联七台新型发动机的推力向箭体传递，同时确保在该推力下箭体不发生动力学失稳是该型运载火箭机架研制的关键问题。

本文拟开展某新一代载人运载火箭芯一级七台并联发动机机架在预应力作用下的动响应研究。通过研究机架杆结构在大推力作用下的几何非线性表达式，分析由发动机推力产生的预应力对机架结构频率和模态的影响，在此基础上，开展机架结构的材料等效替换方法研究。拟采用预应力结构频率优化方法，在维持结构整体预应力模态不变的条件下，实现机架结构的材料等效替换，从而有效降低多机并联机架动静联合试验成本。最后，开展某型号七机火箭发动机机架结构的材料等效替换应用研究。在不改变结构传力路径的情况下，实现不锈钢和钛合金的等效替换，并通过优化替换后机架关键部位尺寸等参数来确保低阶预应力下的动力学的特性不发生变化。

1 机架结构非线性振动理论分析方法

新一代载人运载火箭芯一级并联安装七台发动机的机架结构，是一种基于推进剂贮箱箱底与箭体壳体联合传力的高效率推力传递结构方案，其主要的传力结构，为主梁-机架杆-传力环结构。火箭发动机产生推力，由该传力结构向上方箱底和壳体传递。

多机并联发动机机架结构，一般采用高强度金属材料焊接而成的梁结构。在工作时需承受大推力载荷，容易发生非线性变形，导致其动力学特性相对复杂。因此，机架的动力学特性研究中需考虑梁结构的非线性振动因素。当梁结构发生大变形产生几何非线性时，其侧向刚度会相应地变化，本文仅考虑几何非线性条件下机架梁结构的非线性动力学行为[18]。

不失一般性，以三维杆梁结构为例，其轴向应变由轴向位移u和横向位移v,w以及横向曲率所产生。其中，由轴向位移u和横向位移v,w所产生的轴向应变为[19-21]：

(1)

横向曲率产生的轴向应变为：

(2)

可推导出应变矩阵为：

(3)

式中：γ为剪切应变，式右边第一项为线性项，第二项含有高阶非线性项。

根据最小势能及变分原理，空间梁结构几何非线性能量方程为：

(4)

式中：B为几何矩阵；σ为应力矩阵；p为载荷矩阵。

根据式(3)可知，应变矩阵ε由线性和非线性两项组成。因此，根据几何应变公式，几何矩阵B可展开为:

B=B0+BL

(5)

(6)

式中：N′i(x)为空间梁单元位移插值向量对x的偏导数，其中i=u,v,w；d为单元节点位移向量。

通过式(4)和(5)变分，可以推导出预应力和非线性条件下的单元刚度矩阵KT，可以表示为：

KT=K0+KL+Kσ

(7)

其中，小位移的线性刚度矩阵K0、初位移刚度矩阵KL、几何刚度矩阵Kσ分别为：

将上述非线性刚度矩阵代入结构动力学运动方程可知：

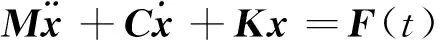
(8)

预应力条件下的结构特征值方程为：

Kφi-λiMφi=0

(9)

综上，预应力模态分析，先需要开展预应力载荷的非线性静力分析，之后提取非线性静力分析的刚度矩阵以计算预应力条件下的特征值。

2 频率尺寸优化分析方法

2.1 预应力材料物性和结构截面尺寸等效替代方法

考虑钛合金机架实际加工时间及制造成本，在不影响试验效果的基础上，可以采用成本较低的材料进行等效替换，比如将钛合金材料替换为不锈钢材料。由于二者的模量、密度等参数不同，直接替换易导致动力学特性发生较大变化，尤其是预应力模态的变化。因此，在保留当前已有的设计下，可通过优化结构截面尺寸消除材料属性所带来的低阶预应力模态的误差。

不失一般性，本文以二维受轴向力作用的简支梁为例，推导材料物性和结构尺寸等效替代公式。

假设轴向力作用下的梁初始变形满足弯曲变形的平截面假定，则弯曲变形运动方程满足：

(10)

式中：m为分布质量；u为梁上某点的竖向位移；P为作用在梁上的外力；EI为梁的抗弯刚度；N为轴向预应力；t为时间。

代入简支梁边界条件，可得预应力下固有频率算式为[22]：

(11)

式中：n为频率阶数；L为简支梁长度。

材料替换后，为保持各阶自振频率不变，则有：

(12)

式中：E1I1和m1分别为材料替换前的抗弯刚度和单位质量；E2I2和m2分别为材料替换后的抗弯刚度和单位质量。

化简可得：

(13)

式中：ρ1和A1为材料替换前的密度和简支梁截面面积，ρ2和A2为材料替换后的密度和简支梁截面面积。

式(13)中，截面面积A和惯性矩I与结构截面的尺寸有关，密度ρ和模量E为材料的物性。对于简单结构，可根据材料替换前后的物性参数计算出替换后材料的等效截面尺寸，可实现保证频率不变情况下材料等效替换。

2.2 机架频率优化列式

对于复杂的机架结构，可以采用预应力条件下机架频率优化方法实现等效材料的等效替换。

以机架总体质量最小为目标函数，机架关键部位的尺寸参数为设计变量，预应力频率上下限以及结构整体刚度与初始设计的刚度比作为约束函数。由此，可以得到最终的优化列式为：

(14)

2.3 频率优化灵敏度分析

根据结构动力学方程特征值方程[23]：

Kφ=ω2Mφ

(15)

式中：φ为振型。两边同时进行微分并乘以φT可得：

(16)

(17)

式(17)代入式(16)得：

(18)

考虑振型φ对于M是归一化的，即：

φTMφ=1

(19)

则可得：

(20)

式(20)为结构的固有频率灵敏度列式。

2.4 非线性条件结构频率优化设计流程

结合上述几何非线性和频率灵敏度分析，机架预应力条件下的频率优化方法流程如图1所示。首先对材料替换后的模型进行非线性静力计算，通过非线性迭代，提取出新刚度矩阵Kn，再进行预应力模态计算；判断是否满足频率的约束范围，若满足则进行柔度约束的判断，否则进行尺寸优化，并重新进行迭代计算。

图1 机架结构材料替换频率尺寸优化技术路线Fig.1 The technical route about the frequency and size optimization to replace the material of the frame structure

3 算例验证

为验证本文提出材料等效替代公式(11)的有效性，现对简支梁进行预应力频率分析，并将结果与公式推导的理论解进行对比。假设简支梁为长度1800 mm、截面为外径20 mm×10 mm、壁厚1 mm的钛合金方管，材料参数如表1所示。该简支梁受到预应力为轴向力。

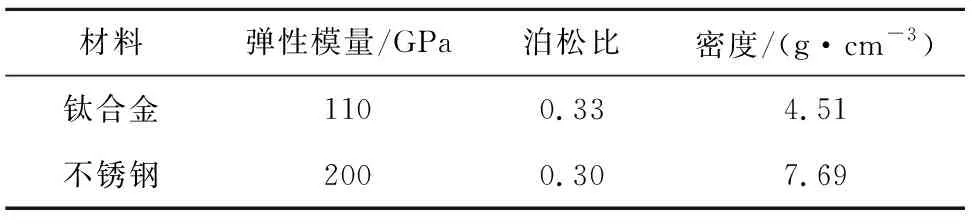
表1 钛合金和不锈钢的材料物性参数Table 1 Material property parameters of titanium alloys and stainless steels

通过仿真计算不同轴向预应力时频率的数值解与式(11)所求得的各阶预应力频率理论解相比较，结果显示，两种解的各阶频率误差均在1‰以内。

将上述钛合金简支梁材料更换成不锈钢，并通过调整简支梁截面壁厚，使得简支梁的一阶预应力频率保持不变。通过式(13)可以获得不同预应力下的不锈钢简支梁截面等效厚度值，并可以进一步获得该厚度值条件下的简支梁预应力频率数值解和理论解。如表2所示，在两种给定预应力下，材料替换后的简支梁一阶预应力频率数值解与理论值误差最大为0.54‰，表明该等效替换公式的有效性。

表2 不同预应力钛合金/不锈钢简支梁频率等效计算结果Table 2 Frequency equivalent calculation results for different pre-stressed titanium/stainless steel simple-supported beam

4 七机并联机架非线性频率分析及优化方法

4.1 七机并联机架预应力模态分析

新一代载人运载火箭芯一级并联安装7台发动机。箭体直径5 m，采用中心1台、周围6台的发动机布局方式。如图2(a)所示，每台发动机与箭体之间通过独立的小机架结构进行连接，共同连接上方的主梁。

图2 七台火箭发动机推力传递结构示意图Fig.2 Layout of the seven parallel engines of the new generation rocket and the rocket thrust transmission structure

新型七台火箭发动机并联机架结构有限元模型如图2(b)所示。模型由主梁、机架杆和传力环三部分组成。主梁与上方的贮箱箱底相连，下方与七组机架杆相连，机架杆下方连接七个传力环。各部件之间均用主从节点绑定的方式进行连接，来模拟焊接以及螺栓连接。综合考虑结构形式以及网格的收敛性，传力环结构采用三维实体单元，共计68964个单元，而机架杆、主梁采用薄壳单元，共计159690个单元。

首先，开展钛合金材料和不锈钢材料机架结构预应力模态分析。二者材料物性参数如表1所示。边界条件和预应力载荷如图3所示，对传力环的下端面进行完全固定，主梁的上端面施加值为8.4×106N的压力，模拟该结构在进行传力时所受载荷。

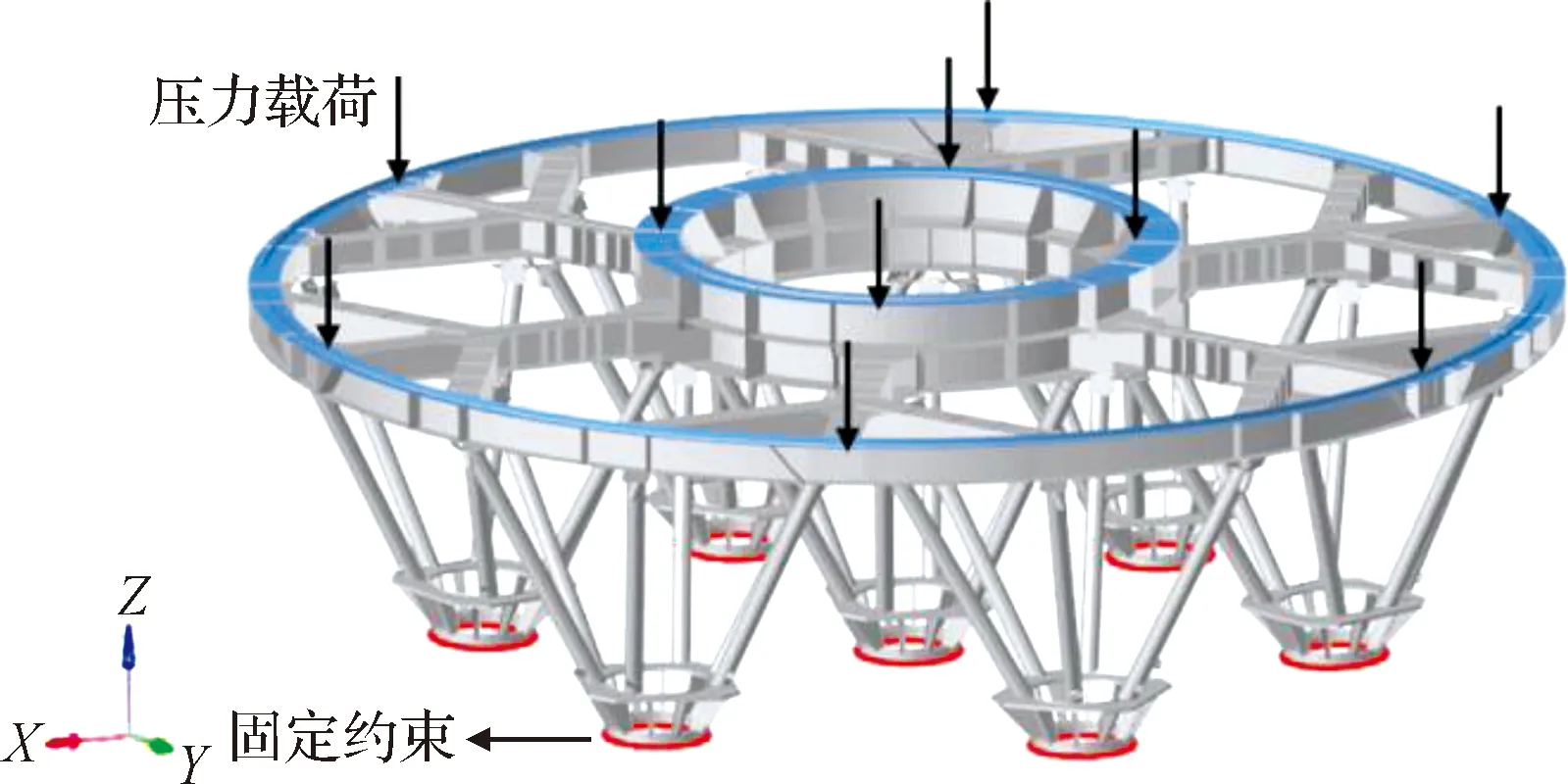
图3 发动机机架结构约束与载荷Fig.3 The boundary and load conditions applied on theengine frame structure

当机架材料为钛合金时，主梁的厚度为14 mm，机架杆的厚度为8 mm，机架整体质量为2539 kg。此时，结构前五阶无预应力模态和预应力基频结果如表3所示，其前五阶中典型振型如图4所示。对比有无预应力下的结构模态分析结果可以看出，预应力对前三阶模态的影响较为明显，尤其在第一阶主梁扭转模态，使一阶频率下降了3.75%，表明推力产生的预应力对机架低阶频率影响较大。在低阶振型中，机架在大推力作用下部分杆件产生了非线性大变形，几何刚度矩阵发生变化，导致机架结构的整体刚度产生了变化。

表3 钛合金材料机架结构前五阶频率Table 3 The first five order frequency of frame structure of titanium alloy material

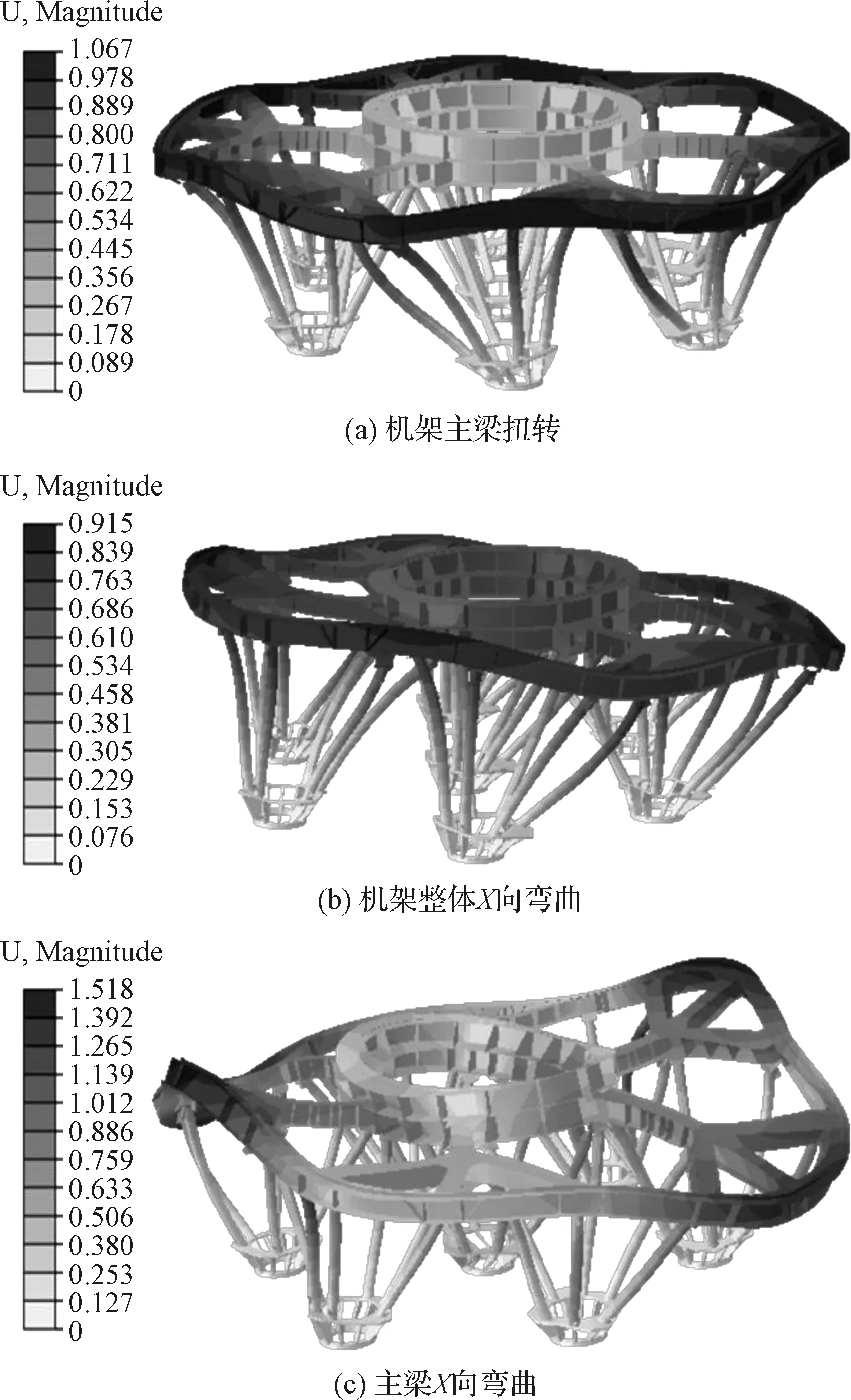
图4 钛合金发动机机架结构预应力模态Fig.4 The pre-stress modal of titanium alloy engine frame structure

为了开展机架材料替换方法研究，本文进一步开展了不锈钢材料机架预应力条件下的动力学特性分析。将机架材料换为不锈钢，各部件厚度保持不变，此时机架整体的质量为4328 kg。将两种材料的预应力模态频率计算结果进行对比，如表4所示。相比于钛合金机架，质量增加了1789 kg，两种材料的机架在预应力作用下，一阶模态的变化幅度达到了5.25%，机架材料的替换使机架整体性能发生了改变。为了消除材料替换带来的结构基频的变化，尤其预应力条件下的非线性变化，需要在不改变机架几何构型的条件下开展钢材机架关键部件尺寸优化研究。

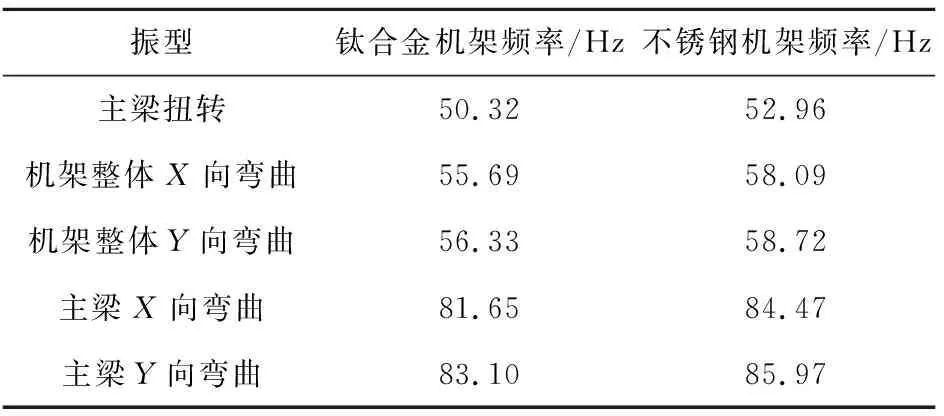
表4 钛合金机架与不锈钢机架预应力模态Table 4 The pre-stress modal of steel frame and titanium frame

4.2 七机机架材料替换尺寸优化设计

钛合金和不锈钢材料物性参数的不同使得机架动力学特性发生变化。本文采用频率尺寸优化方法，在不改变机架整体布局和结构的基础上，通过改变局部结构的厚度尺寸，使得两种材料在低阶预应力频率变化幅度尽可能减小。

频率优化中需要保证结构静强度不发生大的变化。通过两种材料非线性静力下的最大位移之比，可以近似为两种材料结构的刚度之比，即在式(14)中的应变能之比。两种材料下非线性静力计算结果如图5所示，即二者最大位移之比为α=1.845。根据优化列式，对该不锈钢机架结构开展非线性频率尺寸优化。其中，f′1∈(ωmin,ωmax),f′1为钛合金机架一阶预应力模态，为使优化后一阶频率接近于原钛合金材料机架一阶频率50.32 Hz，频率上下界取ωmin=50.3 Hz，ωmax=50.4 Hz；厚度范围限定为2～20 mm。

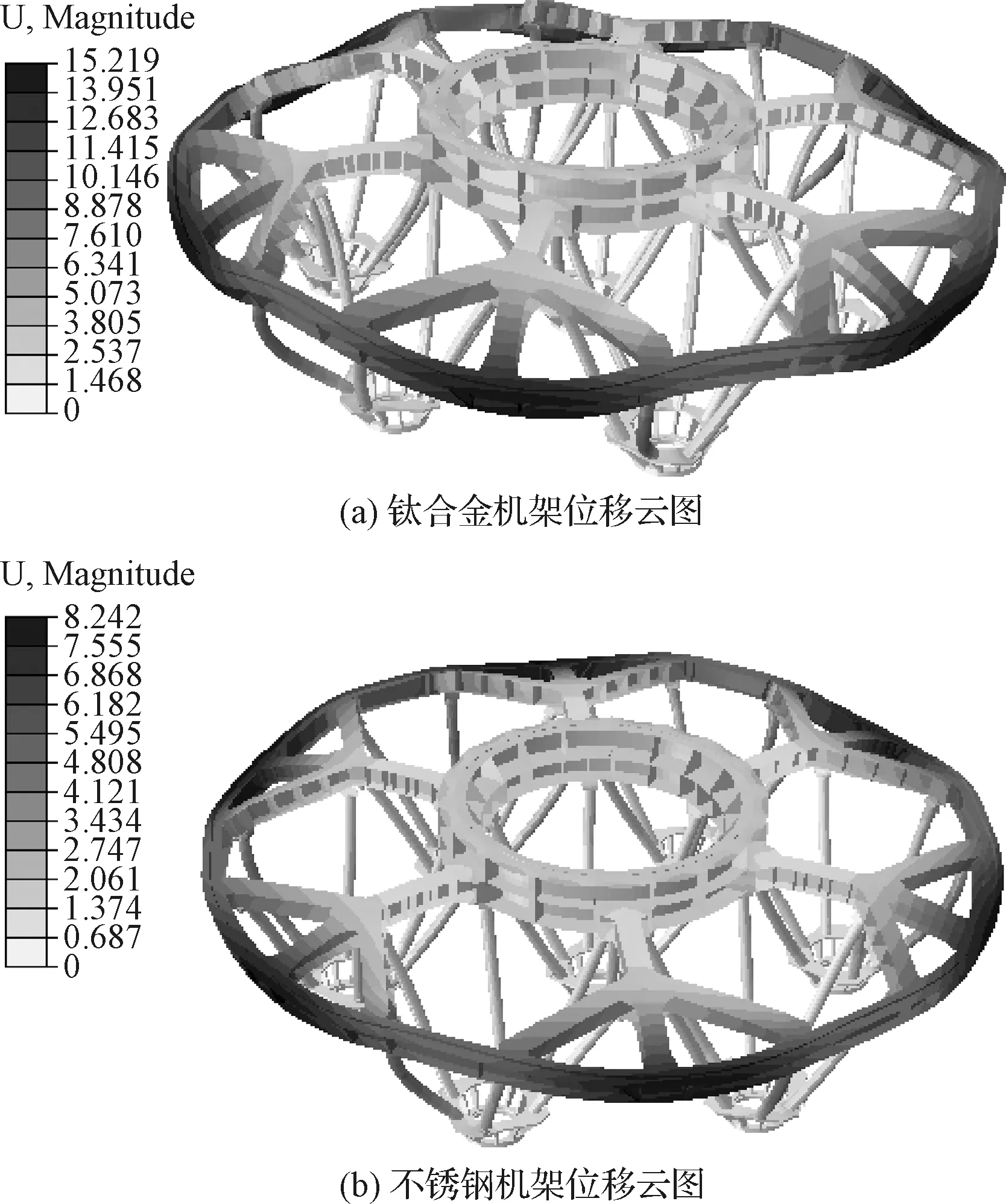
图5 非线性静力计算位移云图Fig.5 Nonlinear static calculation displacementcontour

预应力条件下的优化结果如表5所示，上段主梁的最优厚度为7.76 mm，机架杆的最优厚度为5.20 mm。将优化后与优化前的前五阶模态频率对比，结果如表6所示。

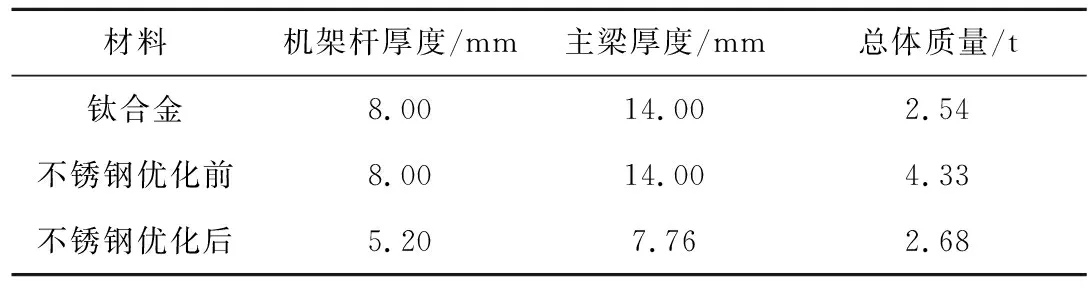
表5 机架关键部件几何尺寸对比Table 5 Comparison of the geometric properties of the key components

表6 机架优化前后的预应力频率对比结果Table 6 Comparison results of pre-stress frequency before and after the size optimization

从表6可以看出，不锈钢机架优化后减重38.19%，机架杆的厚度由原来的8 mm，减小为5.2 mm，减幅达35%；主梁和转接环的厚度由原来的14 mm，减小到7.76 mm，减幅达44.5%。

从式(13)中可知，当材料物性替换前后模量的增量大于密度的增量，为使等式成立，需要减小结构尺寸以缩小材料替换前后的惯性矩。上述优化结果满足此规律，验证了机架结构在动力学试验进行材料等效替代的可行性。

此外，优化后的低阶预应力频率与原始钛合金机架频率基本保持一致，优化后的刚度也与原始结构基本保持一致。另一方面，机架材料等效替代后，机架结构中的机架杆作为主要的承力结构，其厚度的优化空间较小，而主梁的厚度则可以有较大的优化空间，相关结论给后续该类型的机架设计提供了参考。

5 结 论

1) 针对新一代载人运载火箭七台火箭发动机并联机架在大推力作用下的非线性振动问题，开展了非线性条件下预应力结构频率分析。推导了预应力非线性刚度表达形式，应用于并联机架预应力频率分析。在预应力载荷作用下，机架结构的低阶频率相比无预应力情况降低3.75%，随着频率阶次升高，变化幅度降低。

2) 针对动静联合试验中机架材料替换问题，提出了一种预应力结构优化方法，通过优化特征尺寸，可以使得不锈钢与钛合金机架结构在传力路径不变的情况下动静强度的误差显著减小，从而满足动静联合试验的要求。优化结果满足了等效替代公式的规律，证明了该优化方法的可行性。

3) 分析了不同部件尺寸对频率和刚度的影响规律，这为今后对此类多台发动机机架的优化改进方法具有重要的参考意义。