如何巧解初中数学选择题
张伟琴
(杭州市风帆中学,浙江 杭州 310004)
初三的备考教学中,我们发现由于在初一初二时,老师在要求学生订正选择题时往往会让学生写出完整的解题过程,把选择题直接法以外的解法看成是投机取巧,长此以往,学生对解决选择题缺乏正确的思路和方法,没有掌握一定的技巧,见到题目就埋头运算,按简答题的思路去求解,先得到结果后再去和选项进行对照,既费时又容易出错.本文将以例举的方法就如何巧解初中数学选择题进行阐述.
1 排除选项法
采用排除法,观察选择题特点,寻找差异,从四个选项中先排除掉容易判断是错误的选项,然后求得正确答案.
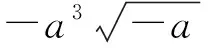

例题2如图1,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( ).


图1
分析考虑图像的“拐点”,边界值,从关键处找突破口,化难为易,化繁为简.
因为等边三角形ABC的边长为3,N为AC的三等分点,所以AN=1.所以当点M位于点A处时,x=0,y=1.
(1)当动点M从A点出发到AM=0.5的过程中,y随x的增大而减小,故排除D;
(2)当动点M到达C点时,x=6,y=4,即此时y的值与点M在点A处时的值不相等.故排除A、C.选B.
2 特例法
根据题目中的条件,选取某个符合条件的特殊值,将字母参数换成具体数值代入,把一般形式变为特殊形式或作出特殊图形,特殊位置进行计算法.
2.1 特殊图形
例题3如图2,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( ).

图2 图3 图4
A.x-y2=3 B.2x-y2=9
C.3x-y2=15 D.4x-y2= 21

2.2 某些特殊值
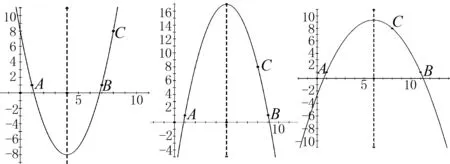
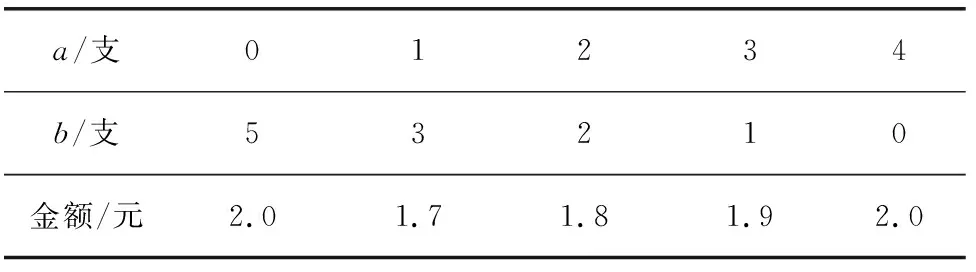
例题4已知a,b为实数,则解可以为-2 分析这个题目选择特例法,取解集-2 例题5如图5,在等腰直角三角形△ABC中,∠ACB=90°,P是线段BC上一动点(与点B,C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.用等式表示线段MB与PC之间的数量关系. 图5 图6 解决与图形或图象有关的选择题,涉及函数和坐标系的,常常需要用到数形结合的思想方法,借助几何直观迎刃而解,达到培养学生直观想象思维的目的. 例题6设函数y=a(x-h)2+k(a,h,k是实数,a≠0),当x=1时,y=1;当x=8时,y=8( ). A.若h=4,则a<0 B.若h=5,则a>0 C.若h=6,则a<0 D.若h=7,则a>0 图7 图8 图9 分析如图7,选项A,图象过A(1,1),根据对称轴h=4,必过B(7,1),这样过A、B、C三点的抛物线,开口向上.如图8,选项B,图象过A(1,1),根据对称轴h=5,必过B(9,1),这样过A、B、C三点的抛物线,开口向下.如图9,选项C,图象过A(1,1),根据对称轴h=6,必过B(11,1),这样过A、B、C三点的抛物线,开口向下.故选C. 枚举法就是列出所有可能的情况,然后作出正确的判断. 例题7小亮去文具店买铅笔和橡皮,铅笔每支0.5元,橡皮每块0.4元,小亮带了2元钱,想尽量多买些铅笔和橡皮,则他有几种不同的购买方案( ). A.2种 B.3种 C.4种 D.5种 分析设铅笔盒的单价为a元,橡皮的单价为b元,则由题意可得0.5a+0.4b≤2 这样计算,可以建立下面的表1,轻松得出D答案. 表1 铅笔盒与皮单价关系表 把题干和选项联合考虑或把选项代入题干进行检验,然后作出判断,后这种方法在做选择题时更常用,更有效. 例题8已知二次函数y=ax2+(2-4a)x-1(a为常数,且a≠0)( ). D.若-1 分析本题出现在选择题的最后一题,属于压轴题,比较难.我们发现A、B两个选项是矛盾的,从选项A中选取a=1代入题干进行检验:当a=1时,y=x2-2x-1,对称轴为x=1,在-1 例题9如图10,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点E,F分别在边AB,AC上,将△AEF沿直线EF翻折,点A落在点P处,且点P在直线BC上,则线段CP长的取值范围( ). A.0≤CP≤4 B.1≤CP≤4 C.1 图10 图11 图12 分析如图10,解题的关键是正确找到点P的位置,通过动手翻折,将△AEF沿直线EF翻折,移动点P,确保“点E,F分别在边AB,AC上”. 从以上的例题我们可以感受到,选择题与简答题有所不同,选择题只求正确结论,只要用合适的方法迅速准确地作出判断即可.我们充分利用选择题的特点,优化解题思路,提高解题的速度及灵活性,才能即准又快解题,为后面做简答题留下充裕的时间,在中考中考出理想的成绩.
2.3 特殊位置



3 数形结合法
4 枚举法

5 验证法

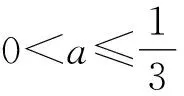

6 动手操作法



