基于UKF 优化多三角加权定位算法的UWB 室内定位系统设计

陈 静, 缪坤坤, FELIX Manirankunda

(安徽理工大学 电气与信息工程学院, 安徽 淮南 232001)

0 引言

超宽带(Ultra-Wideband,UWB)具有时间分辨率高、穿透力强、覆盖范围广、系统复杂度低和抗多径效应良好等优势,测距精度可达到cm 级[1]。 相对于过去常用的红外线定位、超声波定位、WiFi 定位、蓝牙定位和ZigBee 定位等技术,基于UWB 技术的定位精度要高得多[2]。 目前,基于UWB[3-4]技术的室内定位系统得到了广泛应用。

很多学者对视距(Line-of-Sight,LOS)环境下的UWB 定位算法进行了研究,如三边定位算法[5]、Chan 算法[6]和Taylor 算法[7-8],但是上述方法都没有考虑到在室内复杂环境下UWB 定位系统容易受到非视距(Non-Line-of-Sight,NLOS)环境影响的问题。 信号在穿过障碍物时产生的附加延时会降低定位精度[9]。

近些年来,一些学者将传统算法与滤波算法结合,或改进传统算法以减少多径效应与NLOS 环境对定位精度的影响,或提高LOS 下的定位精度。 文献[10]提出了一种简单到达时间差(Time Difference of Arrival,TDOA)算法,将TDOA 定位方程转化为最小二乘形式,然后通过迭代方法计算出标签的收敛坐标。 文献[11]改进了Taylor-UKF 算法,改进Taylor 算法初值计算,并将Taylor 算法的计算值作为无迹卡尔曼滤波(Unscend Kalman Filter,UKF)观测值进行再次计算得到最优标签坐标。 文献[12]提出了Chan-UKF 定位算法,利用Chan 算法进行初步定位,再使用简化UKF 算法对筛选出符合条件的测量值再次进行计算得到最优坐标。

上述文献针对NLOS 环境下定位精度低的问题都提出了相应的解决方法,但是精度仍不够高。 为了进一步提高NLOS 环境下的定位精度,本文提出了一种多三角加权定位算法。 通过多三角加权算法获得更精确可靠的标签坐标,并对所得坐标数据进行UKF,进而得到最优的坐标结果,提高了定位精度。

1 多三角加权定位算法

多三角加权定位算法的基础是传统的三边定位算法[13]。 三边定位算法基于3 个基站获得标签到基站的距离,利用三角形算法计算出标签坐标。 多三角加权算法使用了4 个基站,每3 个基站分为一组,共4 组排列组合,每组基站使用三边定位算法计算出标签初始坐标,对4 个标签初始坐标进行加权计算得到标签坐标。

1.1 三边定位算法

三边定位法如图1 所示。 图1 中,3 个基站的坐标为(x1,y1),(x2,y2),(x3,y3),标签坐标为(x,y),标签与3 个基站的距离分别为d1,d2,d3。 构建方程组为:

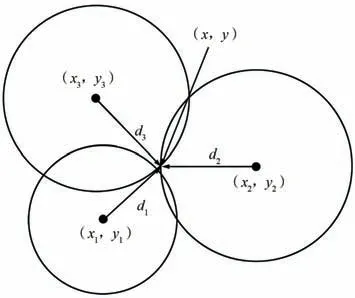
图1 三边定位算法Fig.1 Trilateral localization algorithm

室内定位通常是求取目标在定位区域内的平面坐标,取平行于地面的平面作为定位面,不关注目标高度。 硬件系统反馈的是三维空间的测距值而非平面测距值,需对三维测距值进行降维处理获得平面测距值。

三维距离的平面投影如图2 所示。 图2 中,D为实际测得的三维测距值,d为三维测距值在定位面上的投影,Δh为基站与标签的高度差,基站安装在室内四周且海拔高度一致。 假设基站高度为Z,标签高度设定为h,则Δh=Z-h。 构建的降维方程为:

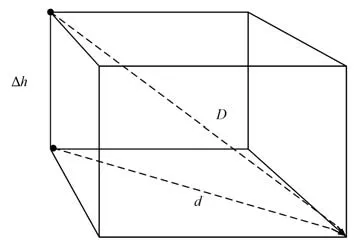
图2 三维距离的平面投影Fig.2 The plane projection of three-dimensional distance

式中,(xi,yi)为基站坐标;(x,y)为标签坐标。

由于定位过程中会对测距值进行降维处理,后面只关注基站和标签的平面坐标。

1.2 多三角加权定位算法

噪声方差与距离之间呈正比关系,距离越远,噪声方差越大[14]。 UWB 信号具有较强穿透性[15],近距离时障碍物造成的NLOS 误差比较小,基站与标签距离越近,其测距值越可靠;远距离时由于信号能量的衰减,UWB 信号的穿透性随之减弱,造成的NLOS 误差会严重影响定位精度。 而多三角加权的思想是使距离标签较近的基站测距值在定位计算中占有较大的权重,距离标签较远的基站测距值在定位计算中占有较小的权重,从而提高定位精度。

多三角加权定位算法示意如图3 所示。 图中,A,B,C,D为定位基站,其坐标分别为(xi,yi)(i=1,2,3,4;分别对应A,B,C,D),标签坐标为L(x,y)。每3 个基站构建一个三角形,这样,可以得到△ABD,△BCA,△CDB,△DAC四个三角形。 通过三边定位算法可以计算出该三角形的标签初始坐标。

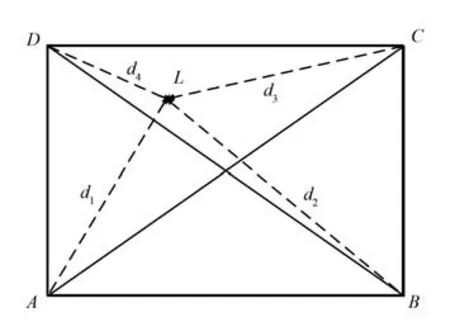
图3 多三角加权定位算法示意Fig.3 Schematic diagram of multi-triangular weighted positioning algorithm

图3 中,以△DAC为例,标签与A,C,D三点的距离分别为d1,d3,d4,r为近距离测距误差,R为远距离测距误差。 重构公式如式(3)和式(4)所示:

求解式(3),可得标签初始坐标:

同理,在△BCA中用三边定位算法求解L点的初始坐标:

由式(4)和式(5)可以看出,不同三角形所得初始坐标的误差构成有着较大差异,三角形中近距离点越多,结果越精确。 而多三角加权定位算法的作用就是找到这些精度高的坐标,并赋予其较高的权值,使其在最终结果中占据较大权重。

设三角形△ABD,△BCA,△CDB,△DAC中的标签初始坐标为(x△1,y△1),(x△2,y△2),(x△3,y△3),(x△4,y△4),初始坐标权值为w△1,w△2,w△3,w△4。 权值计算为:

式中,di为标签到基站的距离。

根据式(6)所得权值,进行加权计算,得到标签坐标:

2 多三角加权UKF

UKF 的理论基础是卡尔曼滤波(Kalman Filter,KF)和无迹变换(Unscented Transform,UT)。 KF 对线性函数有着优良的预测、跟踪效果,但无法很好地处理非线性函数。 而UKF 使用UT 完成非线性函数状态及其协方差矩阵的处理,舍弃了扩展卡尔曼滤波(Extended Kalman Filter,EKF)[16-17]算法的线性化过程,无需计算雅可比矩阵,减少了计算量,提高了滤波精度。

2.1 KF

KF 原理是根据前一时刻的最优结果得到当前时刻的预测值,使用当前时刻的观测值来修正预测值,进而得到当前时刻的最优结果。 KF 方程组包括预测、观测和更新3 个组成部分。

KF 的预测方程如式(8)和式(9)所示。 式(8)表示算法的预测过程,式(9)表示不确定性在系统中传递过程。

式(10)为KF 的观测方程,表示系统获取的观测值,并给出观测矩阵H :

式中,zk为当前时刻的观测值;H 为观测矩阵;x′k为测量状态变量;v 为观测系统误差。

KF 的更新方程如式(11)、式(12)和式(13)所示。 式(11)为卡尔曼增益方程,式(12)为当前时刻最优结果表达式,式(12)中卡尔曼增益kk决定观测模型和预测模型之间的权重,式(13)为协方差更新方程。

2.2 UKF

UT 变换是用一定数量的参数集去近似一个非线性函数的高斯分布。 UT 变换在原先的状态分布中选择一些点,这些点的均值和协方差与原状态分布的均值和协方差相等。 将这些点代入非线性函数中,得到非线性函数值点集,进而求取非线性函数值点集的均值和协方差[18-19]。

UKF 的状态空间模型为:

式中,k为时间变量;Xk和Zk分别为系统状态向量和观测向量;f(·)为状态转移方程;h(·)为观测方程;Wk和Vk分别为系统误差和观测误差,它们的协方差矩阵分别为Qk,Rk。

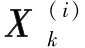
式中,μk为状态向量Xk的均值;pk为状态向量Xk的协方差;r为次级采样因子,用于确保(n+r)pk为非负定矩阵,通常取0;是协方差矩阵pk的平方根;()i是矩阵平方根的第i列。

式中,λ为比例参数,决定了Sigma 点集与状态均值的接近程度;α为离散参数,决定了Sigma 点集的离散程度,通常取0. 01;β为状态分布参数,对于高斯分布β=2 为最优;ωm和ωc分别为均值和协方差的权重。

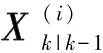
式中,均值为状态向量Xk的预测值;Pk为预测值的协方差。

将预测值和预测值协方差Pk作为统计特性代入式(15)获得新的Sigma 点集,将代入观测方程h(·)得到Sigma 点集观测变换结果,根据计算观测均值k及其协方差P—Zk:

基于式(17)和式(18),计算预测值和观测值的互相关协方差:

式中,i=0,1,…,2l。

式(15)~式(19)为UT 变换过程。

KF 算法是针对线性系统的最优值估计算法,不适用于非线性系统。 在UKF 中,UT 替代了KF 的预测部分去计算状态向量预测值及其协方差,有效地解决了非线性滤波中预测值获取问题。 所以UKF比KF 更适用于非线性滤波环境。

EKF 也可用于非线性滤波,但是UKF 使用UT变换处理非线性滤波时能以二阶或二阶以上泰勒精度逼近后验均值和协方差,而EKF 达不到二阶以上精度。 相比EKF 的线性化过程以及繁琐的雅可比矩阵计算,UKF 比EKF 具有更高的滤波精度和更小的计算量。

通过无迹卡尔曼增益Kk对观测残差(Zk-k)进行加权,进而实现对预测值的修正,得到状态向量的最优结果Xk。 状态更新方程为:

协方差更新方程为:

式中,Pk为最优结果Xk的协方差。

将式(21)和式(22)得到的Xk,Pk作为k时刻的状态向量统计特性,计算k时刻的sigma 点集,进而计算k+1 时刻状态向量的最优结果。

2.3 多三角加权UKF

为了提高定位精度,将UKF 与多三角加权定位算法结合,构建基于UKF 的多三角加权定位算法。算法中,将多三角加权定位算法的定位坐标作为观测值输入到UKF 模型中,分别对坐标的X,Y轴数据进行滤波处理,以获得更高精度的定位结果。 多三角加权UKF 定位算法流程如图4 所示。

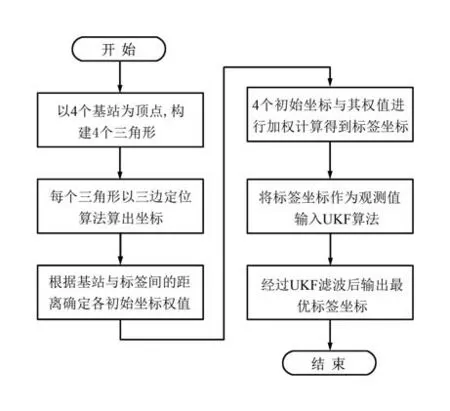
图4 多三角加权UKF 定位算法流程Fig.4 The flowchart of the multi-triangular weighted positioning algorithm based on UKF

UKF 模型如式(14)所示,状态向量为状态的位置和速度信息Xk=[x(k),vx(k),y(k),vy(k)]T,状态转移矩阵F =[1T0 0;0 1 0 0;0 0 1T;0 0 0 1](T为采样周期)。 观测矩阵H 为四阶单位矩阵,观测向量为多三角加权定位输入的位置和速度信息Zk=[xz(k),vzx(k),yz(k),vzy(k)]T。

3 仿真与实验

3.1 仿真设置

为了验证多三角加权UKF 定位算法性能,本文通过Matlab2021a 进行模拟仿真。 定位区域设置为20 m×15 m 的二维平面,基站设置在矩形定位区域的4 个顶点处,基站的坐标分别为(0,0),(0,20),(20,15),(0,15)。 设置测距精度为98%来模拟噪声方差与距离之间呈正比关系,同时添加了均值为0、标准差为1 的高斯随机变量作为噪声。

由于多三角加权UKF 算法会对坐标中X,Y轴的数据分别滤波,需要计算X,Y轴的数据的误差Ex,Ey来判断滤波效果,定位误差Ep来衡量定位精度,即:

式中,(xk,yk)为k时刻标签真实坐标;(,)为k时刻定位算法算出的坐标估计值。

3.2 仿真过程及定位结果

3.2.1 仿真过程

设置4 个基站的坐标分别为A(0,0),B(0,20),C(20,15),D(0,15);设置位标签的起点为(3,11),标签的移动速度为1 m/s,标签的起点和移动速度也是UKF 算法的初值,标签按设定的八边形路径顺时针方向运动,采样周期为500 ms,采样总时长为43 s。 采用了传统三边定位算法、多三角加权定位算法与多三角加权UKF 定位算法对标签进行定位跟踪,其中三边定位算法使用基站A,B,D,其余2 种算法使用基站A,B,C,D。 定位结果如图5 所示。

图5 定位轨迹Fig.5 Positioning track

3.2.2X,Y方向轨迹滤波分析

由图5 的定位轨迹可以得到3 种算法的X轴,Y轴在时间轴上的轨迹数据,如图6 和图7 所示。图中,采样周期为500 ms,共86 个周期43 s。

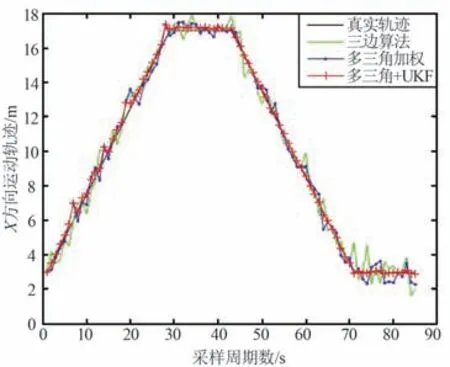
图6 X 坐标轨迹Fig.6 X coordinate track

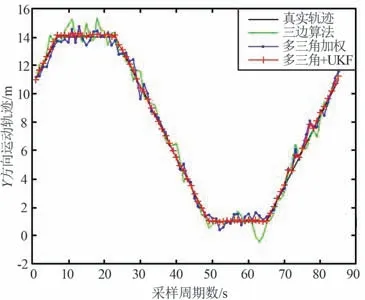
图7 Y 坐标轨迹Fig.7 Y coordinate track

由图6 和图7 可以看出:

① 传统三边定位算法的坐标轨迹基本上跟随着真实轨迹,但存在较大波动;② 多三角加权定位算法跟随效果和波动都有所改善;③ 多三角加权UKF 算法跟随真实轨迹效果最好,减少了很多毛刺,轨迹曲线更加光滑平稳。 3 种算法在X和Y轴上的坐标误差Ex,Ey如图8 和图9 所示。

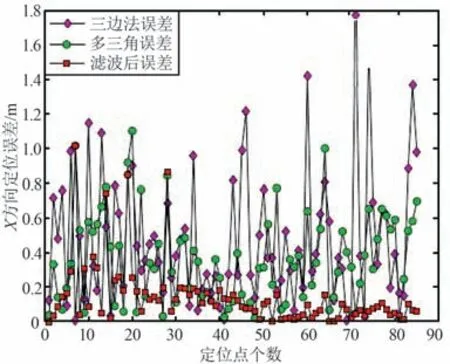
图8 X 轴数据误差Fig.8 X-axis data error

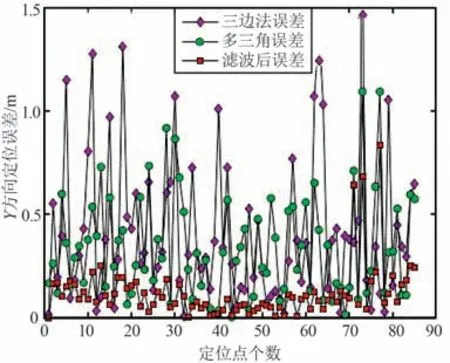
图9 Y 轴数据误差Fig.9 Y-axis data error

根据图8 和图9 可以得到3 种算法在X和Y轴上的平均定位误差,如表1 所示。

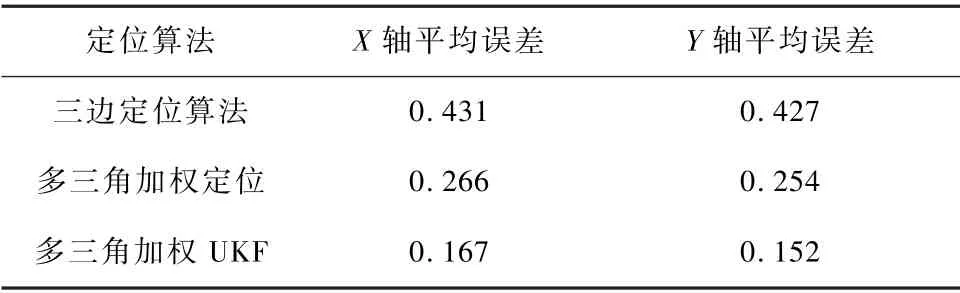
表1 X 和Y 坐标定位误差Tab.1 The positioning error of X coordinate and Y coordinate单位:m

由表1 可知:

① 3 种算法在X轴轨迹上的平均误差分别为0.421,0. 266,0. 167 m;Y轴轨迹平均误差分别为0.427,0.254,0.152 m。

② 多三角形加权定位算法在X和Y轴上的平均定位误差分别比三边定位算法降低了38. 2%和40.4%;基于UKF 的多三角形加权定位算法在X和Y轴上的平均定位误差分别比多三角形加权定位算法降低了38.4%和39.6%,比三边定位算法分别降低了65.2%和64.1%。

结果表明,多三角加权UKF 算法可以获得更好的滤波精度。

3.2.3 定位误差分析

定位误差Ep如图10 所示。

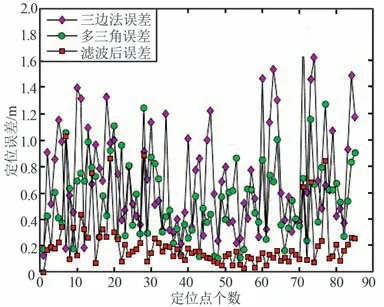
图10 定位误差Fig.10 Positioning error

由图10 可以得到3 种算法的平均定位误差,如表2 所示。

表2 定位误差Tab.2 Positioning errors单位:m

由表2 可知:

① 边定位、多三角加权和多三角加权UKF 的平均定位误差分别为0.613,0.366,0.224 m。

② 基于UKF 的多三角加权定位算法的平均定位误差比多三角加权定位算法降低了38. 7%,比三边定位算法降低了63.3%;多三角加权定位算法的平均定位误差比三边定位算法降低了40.2%。

3.3 实验部分

3.3.1 实验环境

为了验证多三角加权UKF 算法在NLOS 环境下的定位性能,选取如图11 所示的实验环境,2 根水泥支柱作为障碍物为NLOS 测距干扰提供条件,地面上0.6 m×0.6 m 的方形瓷砖提供参考,选取2 根柱子外围的一圈瓷砖地板网格点进行测距采样。 UWB 基站设置在采样点外围的一圈瓷砖网格四周。

图11 定位环境Fig.11 The environment of positioning experiment

定位环境的布局如图12 所示。 基站坐标分别为A0(6.6,0.6),A1(0.6,0.6),A2(0.6,3.6),A3(6.6,3.6)。 基站A0 与PC 相连上传测距信息。 2 根柱子的尺寸为0.65 m×0.65 m 和0.75 m×0.75 m。 起始点坐标为(1.2,1. 2),顺时针方向移动,移动步长为0.6 m,围绕双柱选取了23 个测距点(起点和终点在同一位置)。 部分测距数据如表3 所示。

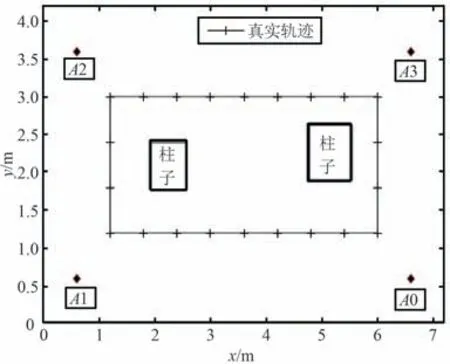
图12 定位平面Fig.12 Positioning plane

表3 部分测距数据Tab.3 Partial ranging data单位:m

3.3.2 实验结果分析

将测距数据输入Matlab 算法脚本进行位置计算,分别计算了基于三边定位算法、三边定位UKF算法、多三角加权定位算法和多三角加权UKF 算法的定位结果,其中三边定位算法和三边定位UKF 算法所用的基站为A0,A1,A2;4 种算法的定位结果如图13 所示。

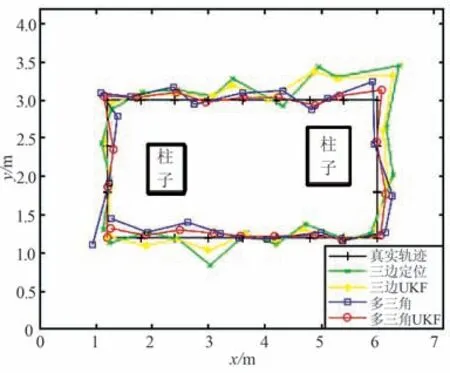
图13 定位结果Fig.13 Positioning results

对比图13 中三边定位算法、三边定位UKF 算法、多三角加权定位算法的定位结果。 由于远距离测距误差和NLOS 测距误差的干扰,三边定位算法在远离基站A0,A1,A2 组成的三角形的一侧有着较大的定位误差,使用UKF 对三边定位算法的结果进行滤波也无法有效减小该类定位误差。 而多三角加权算法使用了4 个基站,通过距离倒数因子加权各个三角形的定位结果,可以有效规避大部分NLOS误差(例如在基站A3 附近的定位点,这些点与基站A0,A2,A3 没有NLOS 误差,与A1 存在NLOS 误差,根据多三角加权算法由基站A0,A2,A3 组成的三角形定位结果会在最终结果中占有很大比重),同时也不会出现当标签远离4 个基站的其中3 个基站时定位结果产生较大偏离的情况。

4 种算法的定位误差如图14 所示。 根据图中数据获得定位误差表(图中三边UKF 与多三角UKF最小值为0 m 是由于滤波算法的初值设置导致的,不作为最小值)。

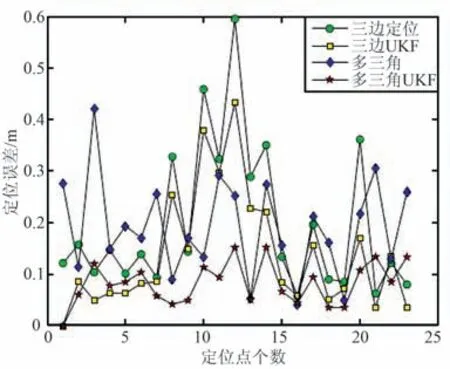
图14 定位误差Fig.14 Positioning error

定位误差如表4 所示。 由表4 可知:

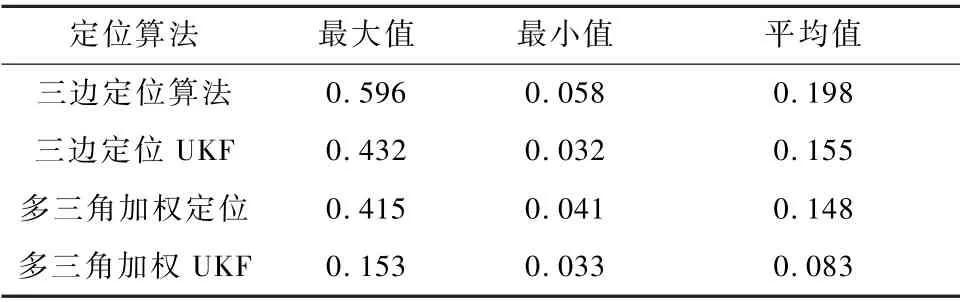
表4 定位误差Tab.4 Positioning errors单位:m

① 三边定位、三边定位UKF、多三角加权和多三角加权UKF 的平均定位误差分别为0. 198,0.155,0.148,0.083 m。

② 4 种定位算法的定位误差最小值相差很小,说明在理想的测距值下使用简单的算法也能获得很好的定位效果。

③ 定位最大误差相比于三边定位的最大误差有了明显降低,同时多三角加权算法配合UKF 显著地降低了最大误差值,提高了定位精度。

结果表明多三角加权UKF 算法可以获得更好的定位精度。

4 结束语

本文基于UKF 优化多三角加权方法进行UWB室内定位,有效解决了室内UWB 定位中的由NLOS导致的定位误差过大问题。

针对由NLOS 导致的定位误差过大问题,提出了多三角加权定位算法,通过4 个三角形计算出标签初始坐标,根据标签到4 个基站的距离计算初始坐标的权值,并进行加权计算得到标签的坐标,提高了近距离测距值在标签坐标中的比重。

为了进一步提高定位精度,提出了多三角加权定位算法与UKF 相结合的算法。 基于UKF 的多三角形加权定位算法明显提高了定位精度,但算法具有较高的复杂度,实时性有待进一步提升。 此外,多三角加权定位的加权方式也是进一步的研究方向。