基于软信息的CCSDS 标准RS 码识别算法

汤文博, 王方刚, 刘 钰, 王宏宇

(北京交通大学 轨道交通控制与安全国家重点实验室, 北京 100044)

0 引言

信道编码识别是通信对抗、通信侦察和智能通信等系统中的关键技术,接收信号在解码前需正确识别编码参数。 里德-所罗门(Reed-Solomon,RS)码是一类具有强纠错能力的前向纠错编码,与交织技术相结合可有效对抗突发干扰和深衰落导致的突发连续误码。 近年来,RS 码被国际空间数据系统咨询委员会(Consultative Committee for Space Data Systems,CCSDS)推荐为遥测(Telemetry,TM)和高级轨道(Advanced Orbiting Systems,AOS)信道编码标准并被广泛应用于遥控遥测等各类通信场景中[1-5]。 在实际工程应用中,为适应不同的帧长以及纠正突发错误,需要对RS 码进行缩短和交织。然而,现有盲编码识别算法中缺少对缩短交织RS码的研究。

目前,RS 码的盲识别方法主要有高斯消元法[6-7]、矩阵分析法[8-9]、欧几里得分析法[10]、伽罗华域傅里叶变换法(Galois Field Fourier Transform,GFFT)[11-13]和二进制等效域硬判决法[14]等。 其中,基于GFFT 的谱累积量分析法理论体系完善,识别性能较为理想。 然而,该算法在高阶伽罗华域(Galois Field,GF)识别性能易恶化,且需要大量的高阶GF 运算,识别速度慢、复杂度高、所需数据量大。 为解决上述问题,王甲峰等[14]提出了一种基于二进制等效域校验和硬判决算法,避免了高阶GF运算,提升了识别速度,在现有的硬判决识别算法中性能较好,然而硬判决算法不能充分利用码字软信息。 Zhang 等[15]提出了GF(2m)上基于对数似然比向量(Log-Likelihood Ratio Vector,LLRV)的RS 码识别算法,有效利用了码字软信息,但是该算法的软信息在高阶GF 处理无法直接利用接收码字的二进制软信息,GF(2m)上LLRV 的计算仍需大量的高阶GF 运算。 另外,上述识别算法仅可识别常规RS码,在识别缩短交织RS 码时失效。

针对CCSDS 标准中的高阶缩短交织RS 编码识别复杂度高、识别性能差的问题,创新性地提出了二进制域基于软信息的缩短交织RS 码识别算法。 与现有的识别算法相比,本文提出的算法解决了同时采用缩短与交织技术的RS 码识别问题,识别性能优于现有的硬判决识别算法并且相比现有的软判决识别算法具有更低的复杂度。

1 CCSDS 缩短交织RS 码编码原理

介绍了CCSDS 标准[1]中规定的缩短交织RS 码编码原理,并给出识别参数的候选集合。 由于标准中规定的缩短交织RS 码可变参数为生成多项式、缩短长度和交织深度,所以本文算法对此3 个参数进行识别。

CCSDS 标准中规定,定义在GF(2m)上的RS 码生成多项式为:

式中,RS 码的阶数m=8,纠错能力E=8 或16,α为GF(2m)的本原元,满足F(α)= 0,本原多项式F(x)=x8+x7+x2+x+1。 由式(1)生成的RS 码,码长为n=2m-1=255,信息符号长度为k=n-2E,记作RS(n,k)。 因此,要识别的RS 码包括RS(255,223)和RS(255,239)。 根据式(1),RS(255,223)的生成多项式为:

RS(255,239)的生成多项式为:

考虑到帧长小于码长的传输场景,标准中规定了缩短RS 码,采用虚拟填充的方法实现。 虚拟填充实现方式如图1 所示。 进行RS 编码之前,首先需要在待编码信息位的开头部分填充q个零码作为虚拟填充部分,其中q为缩短长度,之后进行RS 编码。 由于采用的RS 码为系统码,所以编码后虚拟填充部分和信息位不变,码字尾部增加了校验位。在传输时,虚拟填充部分不传输,仅传输信息位和校验位。 因此,实际传输的码字为缩短RS 码,码长为n-q,信息符号长度为k-q>0,缩短长度候选集为={0≤q≤k-1|q∈}。

图1 传输帧格式Fig.1 Transmission frame format

编码后对RS 码进行交织,标准中规定的交织深度候选集为I={1,2,3,4,5,8}。

完成缩短交织后,在每个RS 码字前添加附加同步标记(Attached Synchronization Marker,ASM),标准中用于 RS 码的 ASM 十六进制表示为352EF853,传输帧格式如图1 所示。

2 基于最大似然估计的码字同步算法

介绍了基于最大似然估计的码字同步算法,并给出利用同步信息对码字起点和缩短长度进行识别的方法。 使用滑动时间窗对接收信号进行采样;计算采样数据与ASM 序列之间的似然函数值,通过最大似然估计实现ASM 位置的识别,进而完成对码字起点和缩短长度的识别。

设传输信号为:

式中,gT为信号生成滤波器;T为符号间隔。 接收信号表示为:

式中,a为信道衰减因数;θ为相位偏移;τ为信道延迟群;w(t)为复高斯白噪声。 接收端的采样信号可以表示为:

式中,Ts为采样时间间隔。

码字同步算法的似然函数表示为:

根据文献[16],该似然函数可以简化等效为:

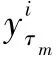
当滑动时间窗取得最优时延估计时似然函数取得最大值,所以时延的最大似然估计表示为:

由此可得ASM 序列位置,根据帧格式可知每个ASM 序列后的第1 个符号为码字起点。 每2 个ASM 序列间的码字数目即为缩短后的码字长度n-q。

3 基于软信息的RS 码识别特征

根据上述候选RS 编码,提出基于等效二进制线性分组码SPP LLR 平均值的识别特征。

3.1 二进制等效校验矩阵的计算

计算缩短交织RS 编码识别度量前,需要根据高斯约旦消元法[17]求取RS 码对应的等效二进制校验矩阵。

首先,通过m和本原多项式F(x)构造GF(2m),之后在GF(2m)内随机生成N>2mn组长度为k的2m进制待编码信息序列,记第t个信息序列为ut=[ut,k-1,ut,k-2,…,ut,0]T,t=1,2,…,N,其中ut,r为2m进制数,r=0,1,…,k-1。 设ft(x)为ut对应GF(2m)上的消息多项式,表示为:

采用生成多项式g(n,k)(x)对ft(x)进行编码的过程可以表示为:

式中,ϕt(x)为编码后的码字多项式,对应长度为n的2m进制码字序列bt=[bn-1,bn-2,…,b0]T。 值得注意的是,此处的码字序列bt是对随机信息序列编码产生的,仅用于计算等效二进制校验矩阵,并非识别时使用的码字序列。 将bt中的每个2m进制数用二进制表示,可以得到长度为mn的等效二进制码字为:

式中,(·)2表示二进制转换运算。 则以g(n,k)(x)为生成多项式对U 编码所得的等效二进制码字矩阵为B =。

利用高斯约旦消元法将B 变换为下三角矩阵Z ,即:

式中,Z 为N×mn维二进制矩阵;Ξ =[ξ1ξ2… ξmn]为mn×mn维二进制列变换矩阵,ξj为的列向量,1≤j≤mn。 存在j=λ1,λ2,…,λm(n-k),使得Z 的列向量zj为零向量,即Bξj=0。 二进制等效校验矩阵H 由Ξ中对应的列向量构成:

3.2 识别特征量的构建

求得二进制等效校验矩阵H 后,根据接收信号构建识别特征量。 假设发送端发送M个RS(n,k)码字,其中第v个码字转换为二进制的比特数据为cv=[cv,1,cv,2…,cv,mn]T,v=1,2,…,M,对应接收端信号为:

式中,n 为服从零均值循环对称复高斯分布的噪声,即n ~CN(0,σ2),σ2为噪声功率。 定义v,i为编码后第v个码字中第i个比特cv,i对应后验概率的LLR 为:

式中,yv,i为yv中第i个元素。 根据奇偶校验关系Hcv=0 可得:

式中,⊕表示GF(2)中的和;hpl表示H 中第p行第l个非零元素的索引;Np表示H 中第p行非零元素的个数;l=1,2,…,Np。 第v个码字中第p个校正子对应的SPP LLR 定义为[18]:

根据公式计算识别数据中所有校正子的SPP LLR并取平均值作为识别度量:

4 缩短交织RS 码识别算法

图2 识别算法原理Fig.2 Principle of recognition algorithm

4.1 码字同步和交织深度识别

首先,利用上述基于最大似然估计的码字同步算法对接收信号进行码字同步,识别码字起点以及缩短长度q^,之后进行交织深度的识别。

在识别I前,首先需要求取g(255,223)(x) 和g(255,239)(x)的公因式:

进而计算生成多项式gfactor(x)对应的二进制等效校验矩阵Hfactor。 之后利用Hfactor和接收信号对I进行识别,识别原理如图3 所示。 识别步骤为:

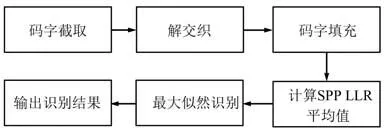
图3 参数识别原理Fig.3 Principle of parameter recognition

① 选取候选参数I′,I′∈I。 由于每个交织码块包含交织后的I′个码长为n-的缩短RS 码字,因此交织码块长度L′=(n-)I′。 在接收信号中截取出整数个交织码块作为识别数据。

② 根据I′对识别数据进行解交织。

③ 根据q^ 对解交织后的数据进行码字填充,得到完整码字软信息序列。 由于在缩短RS 码编码时虚拟填充部分为全0,所以在等效二进制域进行码字填充时cv,i应填充0,根据式(16),码字软信息ℓv,i应填值为+∞,实际填充时可以采用较大的正数,本文采用双精度浮点数类型的最大值。

④ 根据公式,利用Hfactor和码字软信息计算候选参数为θ′时SPP LLR 平均值为:

⑤ 用最大似然识别器进行参数识别,输出识别结果:

4.2 生成多项式识别

在识别生成多项式前,需要根据识别结果和对接收码字进行解交织和码字填充,将缩短交织RS码恢复为常规RS 码,并根据g(255,223)(x)和g(255,239)(x)分别计算对应的等效二进制校验矩阵H(255,223)和H(255,239)。 之后利用恢复出的数据对RS码生成多项式进行识别,识别流程为:

① 利用H(255,223)和恢复的RS 码字软信息,计算SPP LLR 平均值为:

类似地, 利用H(255,239)和码字软信息计算S(255,239)。

② 若S(255,223)>S(255,239),则识别结果为g(255,223)(x);否则,识别结果为g(255,239)(x)。

5 仿真验证

采用CCSDS 标准[1]中规定的缩短交织RS 码进行仿真试验,测试本文提出的基于软信息的缩短交织RS 编码识别算法性能,同时与二进制等效域硬判决算法[14]和基于GFFT 谱累积量算法[12]的识别概率进行对比。 首先,测试缩短交织RS 码识别算法的整体性能;之后,分别测试码字同步算法性能、交织深度识别算法性能以及码字生成多项式识别算法性能;最后,验证数据量对本文所提识别算法性能的影响。 仿真中,信号调制方式采用BPSK,经过AWGN 信道,采用1 000 次蒙特卡罗实验,统计正确识别概率,不失一般性,假设发送功率为1,信噪比定义为SNR=。

5.1 缩短交织RS 码的识别

缩短交织RS 码的识别正确概率随信噪比的变化曲线如图4 所示。 仿真中,发送RS 码字数目为500。 由仿真结果可知,当信噪比大于6.1 dB 时,本文提出的算法正确识别概率可达90%以上。 在使用相同数据量进行识别时,本文所提算法的识别性能明显优于对比算法。 对比文献[14]硬判决算法,有0.1 dB 性能增益;相较于GFFT 谱累积量算法,有0.6 dB 性能增益。

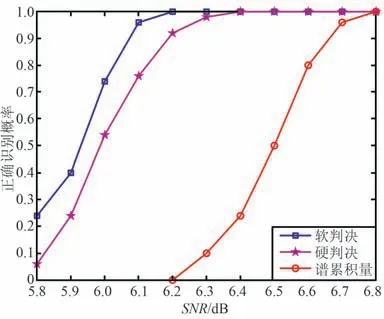
图4 缩短交织RS 码识别性能Fig.4 Recognition performance of shortened interleaving RS code

5.2 码字同步

码字同步算法的识别正确概率随信噪比的变化曲线如图5 所示。 仿真中,发射RS 码字数量为500。 由仿真结果可知,当信噪比大于-3. 5 dB 时,码字同步的正确概率可达到90%以上。

图5 码字同步性能Fig.5 Performance of codeword synchronization

当信噪比大于0 dB 时,码字同步算法的正确识别概率达到100%,可以消除码字时延对识别性能的影响,与图4 进行对比分析可知,码字同步算法性能不是限制识别算法整体性能的主要原因。

5.3 交织深度的识别

本节中固定生成多项式为g(255,223)(x),发送RS码字个数为500,测试交织深度识别算法性能。 本文所提算法与对比算法对交织深度的正确识别概率随信噪比的变化曲线如图6 所示。

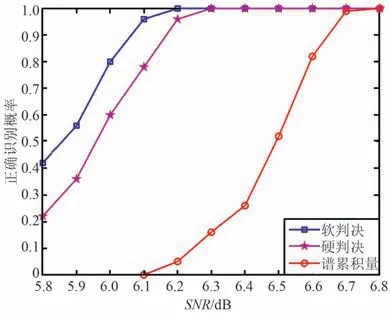
图6 交织深度识别性能Fig.6 Recognition performance of interleaving depth

当信噪比大于6.1 dB 时,本文所提算法对缩短交织参数的正确识别概率可达90%以上。 对交织深度进行识别时,本文所提算法比硬判决算法有0.1 dB 性能提升;比GFFT 谱累积量算法有0. 6 dB性能提升。

5.4 生成多项式的识别

本文所提算法及对比算法对生成多项式进行识别时正确识别概率随信噪比的变化曲线如图7 所示。 仿真中等概率发送未经交织和缩短的常规RS(255,223)或RS(255,239)共1 000 次,每次发送500 码字,统计正确识别概率。 当信噪比大于6 dB时,本文所提算法对生成多项式的正确识别概率达90%以上。 对生成多项式进行识别时,本文提出算法对比二进制等效域硬判决算法有0. 1 dB 的性能增益,对比GFFT 谱累积量算法有0. 2 dB 的性能增益。

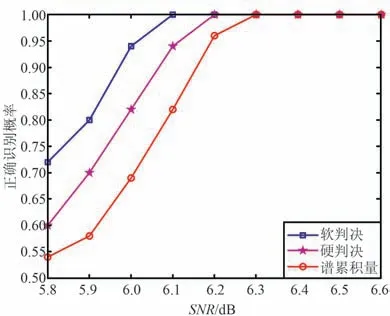
图7 生成多项式识别性能Fig.7 Recognition performance of generator polynomial

5.5 数据量对算法性能影响

分别采用码字数量M=100,200,300,500 对本文所提识别算法进行仿真,结果如图8 所示。 仿真结果显示,当M=100 时,达到90%以上的正确识别概率需要信噪比大于6. 3 dB;当M= 500 时,达到90%以上的正确识别概率需要信噪比大于6. 1 dB。由此可知,随着码字数目增加,所提算法的正确识别概率升高。 所以当信噪比较低时,可以尝试增大识别所用数据量以提高正确识别概率。

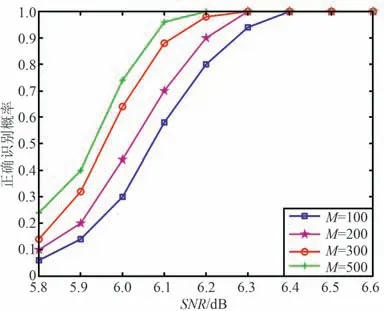
图8 码字数目对算法影响对比Fig.8 Recognition performance comparision of different amount of codeword

5.6 复杂度分析

对所提算法的复杂度进行分析。 首先,码字同步的复杂度为O(n),对交织深度进行遍历的复杂度为O(|I|),之后需要计算每组缩短交织参数下的SPP LLR 平均值,设H 中非零元素的数量为:

根据式(24)可知,计算每个RS 码字中SPP LLR 的复杂度为O(NH)。 计算M个RS 码中所有校正子LLR 的复杂度为O(MNH)。 因此,交织深度识别算法的复杂度为O( |I|MNH)。 类似地,对生成多项式识别的算法复杂度为O(MNH),所以所提算法整体复杂度为O(|I|MNH)。 由于交织深度候选集较小,所以识别算法的时间复杂度较低,适用于对实时性要求较高的识别系统。

6 结束语

本文提出了一种对CCSDS 标准中规定的缩短交织RS 码进行识别的算法,解决了现有识别算法无法识别缩短交织RS 码的问题,采用等效二进制域避免了复杂的高阶GF 运算,具有较低的运算复杂度。 此外,利用码字软信息对现有的基于二进制等效域硬判决的算法进行改进,提高了识别算法的准确率。 仿真结果表明,相等数据量下,所提基于软信息的缩短交织RS 码识别算法相较于二进制等效域硬判决算法性能提升了0. 1 dB,相较于GFFT 谱累积量算法性能提升了0. 6 dB。 另外,本文研究基于BPSK 调制方式和AWGN 信道模型,关于更为复杂的调制方式和信道模型等问题将在今后的研究中进行讨论。