基于递归分解的因果结构学习算法

蔡瑞初，张文辉，乔 杰，郝志峰，2

（1.广东工业大学 计算机学院，广州 510006；2.汕头大学 理学院，广东 汕头 515063）

0 概述

从观测数据中推断变量之间的因果关系是当今数据科学研究的热点［1-2］。因果关系发现的研究可以揭露数据的产生机制，而数据产生机制对现实中的预测和干预问题有着极其关键的作用。在现有的研究中，因果关系发现方法应用于生物医学、教育学、经济学、流行病、气象学等［3-4］多个领域。

传统因果关系方法的研究是通过随机控制实验进行因果关系学习，但实验所需费用高，或现有技术无法实现。因此，基于观察数据的因果结构学习方法备受关注。PEARL 等［5］从图模型的角度给出一套因果关系发现的语言，提出一种因果图模型，其中，节点表示变量，节点之间的有向边表示变量之间的因果关系。基于该模型，PEARL 和SPIRTES 等［5-6］提出基于约束的因果结构学习方法。该方法在忠诚性等假设下［7］，通过条件独立性检验学习因果结构。虽然这类方法能够取得较准确的结果，但是存在马尔可夫等价类问题［8］，即部分因果关系无法被识别。马尔可夫等价类在概率图模型中指具有相同条件独立，其变量和因果骨架相同，但方向不确定的结构。假设由三个随机变量x，y，z组成的骨架x-z-y存在相同的条件独立性P(x|z)P(y|z)=P(x，y|z)，则可能存在3 种不同的结构：x→z→y，x←z←y，x←z→y。

此外，基于约束的因果结构学习方法在对条件候选集搜索时存在复杂度高的问题［9］。BERGSMA等［10］提出在连续变量的条件独立性检验中，随着变量数量的增加，对条件候选集的搜索复杂度将呈指数级增长。在该过程中，随着变量数的增长，算法中变量条件独立性检验条件集的数量也呈指数增长，使得算法的计算复杂度急剧增大。当条件集Z的数量不断增大时，条件独立性检验的正确性有待验证，同时极有可能出现第二类错误，即使变量间互相依赖，也可能被预测为相互条件独立。当条件集数量增加，而样本量不足时，会增加噪声或其他变量对无关变量的影响权重，使得原本相互不独立的变量变为独立关系［11］。

针对这类问题，研究人员提出采用递归分解的方法进行因果结构学习［9，12-15］。这类方法的主要目标是把一个问题递归地分解到两个或多个规模更小的子问题空间中进行高效求解。但是，该类方法仍无法解决马尔可夫等价类问题。

通过对实际场景数据的分析，本文发现在很多现实数据（如社交网络、基因调控网络等）中变量间的关系较稀疏，其组成的因果结构也呈现稀疏性［16］（即每个变量的平均父亲节点数量为2）。因此，结合实际场景数据的特征，本文提出一种基于递归分解的因果结构学习算法CADR，在高维小样本的数据中更高效地进行因果结构学习。基于观测样本的稀疏性，设计一种新的递归分解算法，减少条件候选集的数量，使得条件独立性检验更可靠。基于现有加性噪声模型（Additive Noise Model，ANM）的噪声和数据产生机制假设，解决条件独立性检验中存在的马尔可夫等价类问题。根据递归分解算法所得到的变量子集和加性噪声模型，提出一种学习完全定向的有向无环图（Complete Directed Acyclic Graph，CDAG）方法。

1 相关工作

传统因果结构学习的方法（如IC［5］、PC 算法［6，17-18］等）通过对变量进行条件独立性检验，因存在马尔可夫等价类问题，只能学习因果结构的基本框架，无法学习到真正的因果关系。此外，大多数现有的因果结构学习方法都是在假设样本量足够的前提下进行研究。部分因果结构学习方法虽然对小样本的因果关系发现进行研究［19］，但是实际上在一些高维、小样本数据（如基因表达数据）上的实验效果表现不佳。

针对高维数据的因果关系发现问题，研究人员通过缩小条件候选集的搜索范围，并采用递归分解的方法进行因果关系发现。这类方法的主要目标是将一个总问题递归地分解为两个或多个规模更小且解法相同的子问题，从而提高求解效率。

在XIE 等［12］提出的框架中，对于随机变量集合V：首先，通过条件独立性检验学习每对随机变量在给定其他所有节点集条件下的独立性，得到一个无向独立图（Undirected Independence Graph，UIG）；其次，根据条件A⊥B|C，其中A，B，C⊆V，从UIG 中找出一个分解V={A，B，C}，把集合分解为更小的两个子集V1=A∪C和V2=B∪C，再分别学习这两个子集的UIG，并将其分解为更小的子集，递归地执行该分解过程，直到子集无法再被分解；最后，通过基于约束的方法（如IC、PC 等算法）尽可能多地确定剩余无向边的方向。之后，把这些局部因果结构合并成一个全局因果结构。这种方法摆脱了传统方法对样本量的依赖，但每次学习UIG 的条件集是除了节点对以外的其他所有节点，可能会降低条件独立性检验的准确率。LIU 等［14］通过基于搜索评分的方法来学习UIG，并取得较好的效果，但是在高维样本中，通过搜索评分的方法学习UIG 的计算复杂度不断增大。

条件独立性检验的方法是通过检测V-结构来判断局部结构的因果方向，但因无法区分马尔可夫等价类问题而学习到完全有向的因果结构。针对该问题，研究人员提出加性噪声模型的方法，通过对噪声和数据产生的机制进行假设，根据观测数据拟合噪声，并判断其与原因变量是否独立，从而确定因果方向。这类方法的关键是对噪声和数据产生机制进行假设。根据变量的数量将现有方法分为两类：1）两个变量因果方向判断方法，如非线性非高斯模型［20］、基于回归的模型［21］、基于核空间的方法［22-23］等；2）三个及以上变量的因果方向判断方法，基于HSIC 的方法［24］、基 于KCIT 的方法［25］、基于ReCIT 的方法［11］等。在高维小样本的情况下，因为这些方法需要大量计算变量与联合分布之间的条件概率统计，要求样本量必须充足，所以其实验效果表现不佳。

2 基于递归分解的因果结构学习

2.1 相关符号与概念

令G=(V，E)表示由变量集V={v1，v2，…，vn}组成的有向无环图（Directed Acyclic Graph，DAG），D={X1，X2，…，Xn}表示观测数据集，pa(vi)表示节点变量vi的父亲节点。两个不相邻节点vi和vj之间的路径（path）l表示该路径上的第一个节点变量为vi，最后一个节点变量为vj，同时在该路径上任意两个相邻节点都存在边相连。在这样的路径中，vi是vj的一个祖先节点，vj是vi的一个子孙节点。

定义1在G=(V，E)中，如果在两个不相邻的变量vi和vj之间存在路径l并满足以下条件：

1）l包含一条链vi→z→vj或一个分叉vi←z→vj，其中，z∈Z。

2）l包含一个碰撞（又称V-结构［6］）vi→z←vj，其中，z及其子孙节点都不包含在Z中，则称变量vi与vj被Z集合d-分离，或称变量vi与vj被Z集合阻断。

LIU 等［14］指出，d-分离可以被扩展到变量集中，在忠诚性假设下，如果存在两个不相连的变量集A和变量集B，则满足：∀μ∈A，∀ν∈B，μ、ν被Z集 合d-分离，则变量集A和变量集B被Z集合d-分离。

基于上述定义，本文给出因果关系的相关定义。根据PEARL 的图模型理论，其对于因果贝叶斯网络的定义［5］为：

定义2令P(v)表示变量集V的分布，Px(v)表示变量v经过干预do(X=x)后得到的干预分布，其中，X⊆V，即将部分变量v的集合X值设为某个常数x，P*表示干预分布Px(v)和非干预分布P(v)的集合。在一个DAG 中，对于所有Px∈P*，当且仅当DAG 满足以下三个条件，则称G是分布P*相对应的贝叶斯因果网络：1）Px(v)是G的马尔可夫类；2）对于所有Vi∈X，当vi与X=x一致时，则Px(vi)=1；3）对于所有Vi∉X，当pai与X=x一致时，则Px(vi|pai)=P(vi|pai)，其中，pai表示变量vi的父亲变量。

2.2 算法框架

本文基于因果图模型，给出因果分解的定义。

因果分解实例示意图如图1所示，假设图1（a）由变量集V学习得到的无向独立图，则它的因果分解为图1（b）所示的5 个子集：C1={V1，V3，V4}，C2={V3，V4，V6}，C3={V6，V7，V8}，C4={V3，V6，V7}，C5={V2，V3，V5，V7}。

图1 因果分解实例示意图Fig.1 Schematic diagram of example for causal decomposition

因此，变量集V的因果结构学习问题可以被转换为m个子集{C1，C2，…，Cm}上的子结构学习问题。该分解过程可以被递归地执行，直到子问题小到预先设定的特定阈值θ。本文提出的递归因果结构学习算法CADR 如算法1 所示。

算法1递归因果结构学习算法CADR

该算法的输入包括样本集D、变量集V、因果分解阈值θ，以及特定的因果结构学习算法Ag。当分解后的子问题足够小（达到阈值θ）时，递归分解结束。同时，Ag用于从无法被分解的子问题中进行因果关系发现；否则，继续分解为m个更小的子集。算法1的关键是找到一个因果分解C={C1，C2，…，Cm}。

2.3 因果分解学习

CADR 算法的关键是通过学习得到因果分解。为识别输入变量之间的潜在因果分解，本文采用条件独立性检验方法得到因果分解，其详细过程如算法2 所示。

算法2寻找因果分解

首先，通过条件独立性学习变量集V={v1，v2，…，vn}的一个无向独立图A，表示各变量之间的条件独立性（是否有边连接），Aij=1 表示变量vi和vj之间有边连接，在2.4 节将会给出学习UIG 的详细过程；然后，利用XIE 等［12］提出的方法，把变量集V分解成m个团（cliques）：C={C1，C2，…，Cm}，即需要寻找的因果分解。

本文通过上述方法将高维复杂的因果结构学习任务分解到合适的维度上进行学习，缩小条件独立性检验的搜索空间，进而获得更精准的因果结构。

2.4 无向独立图学习

现有基于马尔可夫毯［27］发现算法和偏相关方法都可用于无向独立图的发现，然而，基于马尔可夫毯的算法因恢复出精确的道德图，导致算法复杂度增大。在实际中，除道德图的边和骨架的边以外，一些额外的边在UIG 中也是允许存在的［14］。

基于偏相关的方法只能运用在线性高斯数据中，无法在非线性非高斯的情况下使用。而基于核空间的条件独立性检验方法则适用于非线性非高斯的情况，如HSIC、KCIT 等方法，但是当变量集较大而样本量较少时，条件独立性检验的结果则变得不准确。此外，基于核的方法在样本量较大时，其时间复杂度也较高。针对该问题，STROBL 等［28］基于随机傅里叶特征方法提出非参数条件独立检验算法RCIT。

RCIT 算法通过随机傅里叶特征算法k(x，y)=E[ζ(x)，ζ(y)]，将变量映射到一个低维的欧几里得空间，如式（1）所示：

因此，本文结合RCIT 方法提出一种q-order 条件独立性检验方法。其中，q表示条件候选集S大小的阈值。为构造一个无向独立图A，首先从一个完全有向图出发，在给定条件候选集S的情况下检验两个节点变量vi和vj的条件独立性进行删边操作，如果独立，则删除vi与vj之间的边，即Aij=Aji=0。条件候选集S的大小k从0 开始依次增加，且每次迭代其大小满足：|S|≤q。通过逐步增加条件候选集的大小，可以有效地缩减算法条件候选集的搜索空间，提高算法运行效率。算法伪代码如算法3 所示。

算法3学习无向独立图UIG

2.5 马尔可夫等价类识别

无向独立图学习是基于约束的方法实现的，而基于约束的方法通过依次检验每对节点的条件独立性来判断是否存在边，进而得到一个基本骨架。该基本骨架根据V-结构和其他一些规则，如Meek’s rules［29］尽可能多地确定边的因果方向［30］。但这种做法会存在马尔可夫等价类的问题，无法确定方向的因果边。假设存在一个局部结构x-z-y，且x⊥y|Z，根据定义1，如果存在一个变量z∉Z，且其任何子孙都不包含在Z中，则确定该局部结构为一个V-结构：x→z←y。当z∈Z时，则无法通过条件独立性来确定该局部结构的因果方向，即该结构是一个马尔可夫等价类。在给出定理1 的前提下，V-结构的可识别性可以通过定理2 来保证。

定理1在因果马尔可夫和因果忠诚性假设下，当且仅当两个DAG 具有相同的V-结构时，即两个聚合的箭头，其尾部没有箭头连接，它们在观测上是等价的［5］。

定理2在因果马尔可夫和因果忠诚性假设下，V-结构是可识别的。

证明在因果马尔可夫和因果忠诚性假设下，如果V-结构不可识别，那么存在两个结构G和G'，使得{vi，vj，vk}在G中是V-结构，在G'上不是V-结构，且该两个结构是等价的。根据定理1，若两个结构等价，则一定存在相同的V-结构，所以矛盾。因此，V-结构可识别。

对于通过条件独立性检验方法得到的无向图，可以先识别V-结构，确定相应的因果方向。此时，需要解决的问题：当z∈Z时，如何确定因果方向。

针对这一问题，受因果函数模型的启发，本文考虑利用加性噪声模型识别在马尔可夫等价类变量之间的因果关系，其识别方法通过定理3 来验证。

定理3假设一组变量集合V由非线性非高斯加性噪声模型生成，其所有子集相应的子结构都满足忠诚性假设，且存在两个随机变量x，y∈V以及由其他变量组成的集合Z满足x⊥y|Z，并存在z∈Z与x，y相连。nxz或nyz表示利用z回归x或y得到的残差，当x⊥nxz（或y⊥nyz）成立时，则z是x的原因，即z→x（或z是y的原因：z→y）。

基于定理3，得到马尔可夫等价类的识别方法。首先，根据条件独立性检验得到无向图，结合定义1识别V-结构；其次，在剩余未定向的结构中根据定理3确定其边的因果方向。通过上述方法获取到包含更多因果边信息的因果图，从而解决马尔可夫等价类问题。

2.6 时间复杂度分析

CADR 算法的时间复杂度主要取决于条件独立性检验的次数。在CADR 算法中，原始变量集合V={v1，v2，…，vn} 被因果分解为m个子集C={C1，C2，…，Cm}，且|Cm|≤n，则该求解因果分解集合的时间复杂度为，其中，kmax表示子集变量最多的数量，kmax=max(|C1|，|C2|，…，|Cm|)。同 时，CADR 算法还需要计算每次迭代过程中条件独立性检验的次数。基于无向独立图进行q阶条件独立性检验的每次迭代都需要遍历所有变量对，其时间复杂度为O(nq+2)。因此，CADR 算法的时间复杂度为。当数据维度高于100，q设置为3 时，CADR 可以得到准确的实验结果，且缩短运行时间。

3 实验与结果分析

本文通过大量的仿真数据实验以及真实贝叶斯网络实验来验证CADR 算法的有效性，并与XIE等［12］提出的递归因果结构学习方法（Xie_rec）、传统PC+ANM 的方法（PC_ANM）、ZHENG［31］等提出的非参数因果结构学习方法（Notear_Sob）进行对比。实验指标为召回率（Recall）、精确率（Precision）和F1评分。实验环境为Intel®CoreTMi7-9750H CPU @ 2.60 GHz，编程环境为Python 3.7。

3.1 仿真数据实验

本文在非线性非高斯模型假设下仿真因果贝叶斯网络数据，数据生成方式与CAI 等［13］提出的方法类似。在仿真实验中，首先随机生成一组根节点，其次迭代地随机选择根节点，并将其作为父亲节点来生成后代节点，其数据产生机制表示为：

其中：f(·)表示非线性函数，从{x2，x3，sin(x)，cos(x)}中随机选取；噪声ni服从非高斯分布。

本文的仿真数据实验基于不同维度和样本量设置一系列随机实验，其变量维度范围为var=｛10，20，30，40，50｝，样本大小为n_sample=｛100，200，300，400，500｝。基于不同的参数设置，随机生成因果图，根据非线性非高斯结构方程模型随机生成数据，得到不同参数设置下的样本。

在仿真数据实验中，本文考虑到非线性非高斯加性噪声在维度小于7 时的实验效果较好，因此，当因果分解时子集的大小阈值θ设置为6，在条件独立性检验中，设条件候选集的大小阈值q=3。每个变量维度和样本量的组合数据实验都重复20 次，取每组实验结果的平均值作为评价指标。

不同算法的仿真实验结果如图2 所示。从图2可以看出：CADR 算法的因果结构学习效果比其他三种因果结构发现算法更好。在不同的样本量上（如图2（a）所示），CADR 算法几乎在所有样本量的F1 评分都要优于其他三种算法。同时，本文在不同变量维度的情况下（如图2（b）所示）的实验效果优于其他三种算法的效果。基于递归分解的算法Xie_rec 的F1 评分优于传统算法PC_ANM 和Notear_Sob 算法，且其效果差距随变量数的增加而不断增加。基于递归分解的算法将高维小样本的因果结构学习转化到低维，以有效缓解原本在高维因果结构学习样本量不足的问题。在样本量不变、维度减小的情况下，基于递归分解算法的计算准确率得到提升。在基于递归分解的算法中，CADR 在实验中的F1 评分高于Xie_rec，Xie_rec 方法经过条件独立性检验后，只是通过V-结构和其他一些定向规则来确定因果方向，可能存在部分无法识别的无向边，而CADR 算法可以有效区分马尔可夫等价类，得到一个完全有向的因果结构。

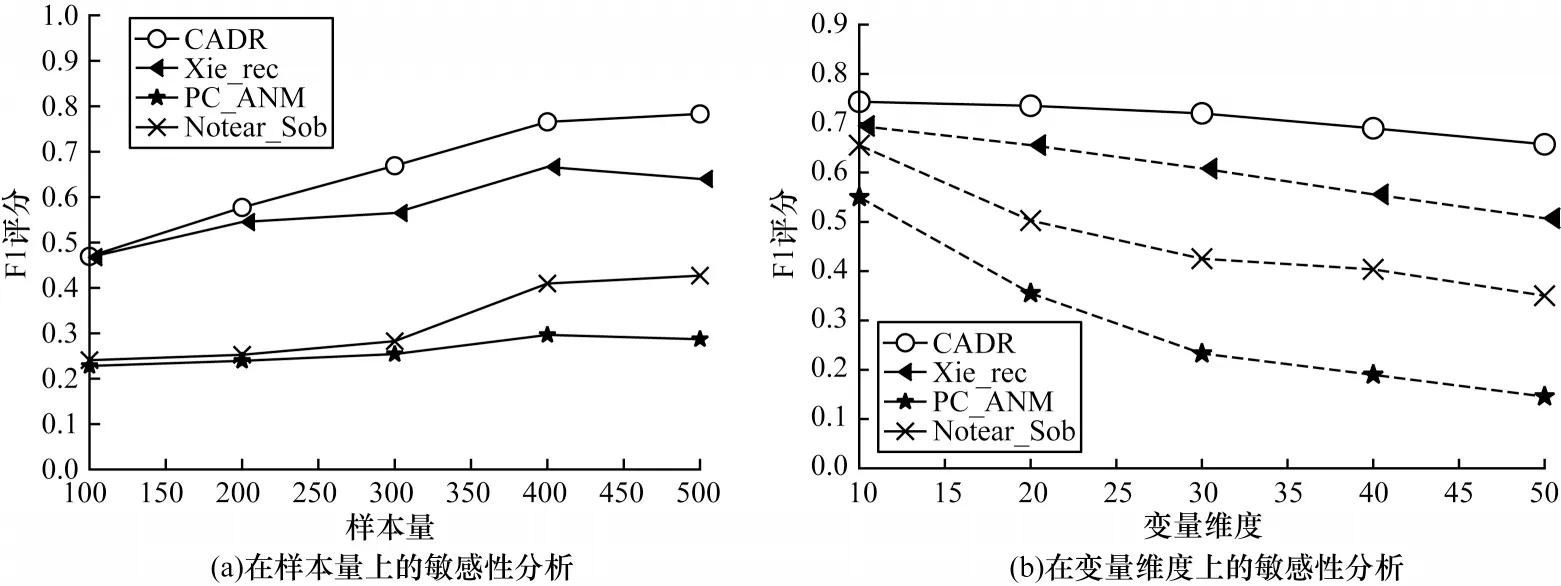
图2 不同算法的仿真实验结果对比Fig.2 Simulated experimental results comparison among different algorithms

3.2 马尔可夫等价类识别实验

为进一步评估CADR 算法在因果推断的优势，本文对比CADR 算法和Xie_rec 算法在因果结构学习的能力。CADR 与Xie_rec 方法的马尔可夫等价类识别结果对比如图3 所示。真实因果图如图3（a）所示，根据该因果图，本文通过非线性非高斯结构方程模型生成数据，并在样本量足够的情况下把两种算法应用到该数据中，以恢复真实因果图。图3（b）和图3（c）所示为由CADR 算法和Xie_rec 算法学习得到的因果图。

图3 CADR 与Xie_rec 方法的马尔可夫等价类识别结果对比Fig.3 Recognition results of Markov equivalence classes comparison among CADR and Xie_rec methods

通过CADR 可以完全恢复出真实的因果图，尽管Xie_rec 能恢复出正确的骨架和V-结构，但无法区分马尔可夫等价类和得到完全有向的因果图。根据定理1，CADR 通过原因变量拟合结果变量以得到噪声，并利用非线性非高斯数据中因果关系的不可逆性得到因果方向。因此，CADR 算法可以有效区分马尔可夫等价类，识别出所有边的方向，得到一个完全有向的因果图。

3.3 真实贝叶斯网络结构实验对比

本文在非线性非高斯加性噪声的模型下，通过对不同的真实贝叶斯网络结构进行对比，并根据实验结果评估本文所提的CADR 算法。这些真实贝叶斯网络结构一般涵盖各种应用，包括医学研究的Alarm 数据集、Pathfinder 数据集、天气预测的Hailfinder 数据集、系统故障诊断的Win95pts 数据集以及智能教学指导系统的Andes 数据集、猪育种系谱Pigs 数据集以及基因调控网络Link 数据集。表1所示为真实贝叶斯网络结构的统计数据。从表1 可以看出：贝叶斯网络结构中变量的父亲节点（最大入度）均不超过6，说明真实因果网络结构具有稀疏性的特点。

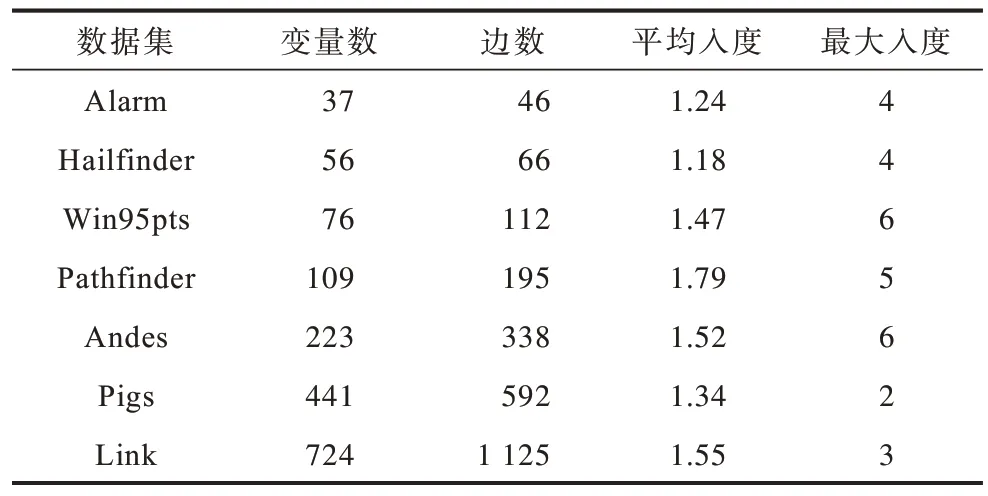
表1 真实贝叶斯网络结构的统计数据Table 1 Statistical data of real Bayesian network structure

当样本量设置为变量数的3 倍时，本文将实验得到的召回率、精确率和F1 评分作为评价指标。真实贝叶斯网络结构的评价指标如表2 所示，加粗表示最优的数据。CADR 算法在所有真实结构上具有更优的精确率和F1评分，验证本文提出的CADR 算法的有效性，特别是在高维的情况下。CADR 算法在不同数据集上的运行时间均低于其他算法。从表2 可以看出：CADR算法在因果结构学习的准确率和效率方面具有较优的效果。实验结果表明，CADR 算法在高维小样本数据的因果结构学习问题上具有较强的识别能力，能够提升因果结构学习的效率和识别正确率。

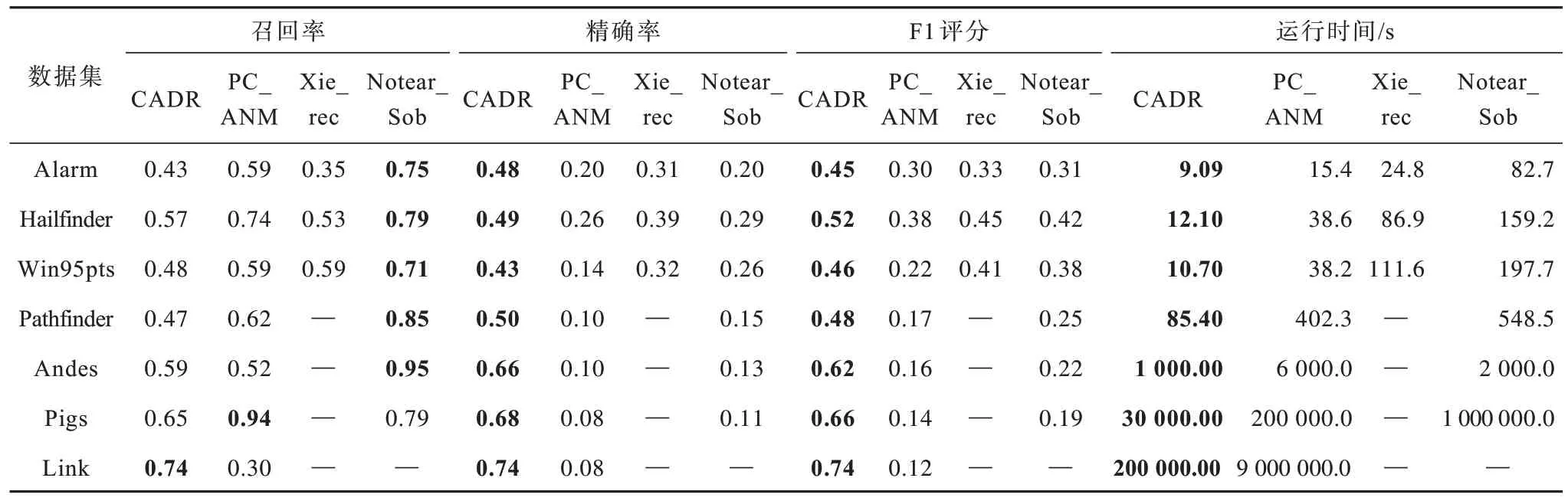
表2 真实贝叶斯网络结构的实验结果Table 2 Experimental results of real Bayesian network structures

4 结束语

本文提出一种基于递归分治方法的因果结构学习算法CADR，用于高维小样本数据的因果关系学习。通过因果分解方法把基于高维变量集的因果推断问题逐步分解为维度更小的子问题。结合RCIT和PC-style 提出一种高效的算法，以得到一个无向独立图，从而减少条件独立性检验的次数。同时，采用递归因果分解把得到的骨架分解为更小的子图，减小下一步条件独立性检验的搜索空间。在此基础上，利用非线性非高斯加性噪声模型的因果关系识别马尔可夫等价类。实验结果表明，CADR 可以得到较为精确的因果图，能有效提高算法的效率和条件独立性检验的准确率。下一步将针对稠密网络的因果结构学习进行研究，以提高CADR 的稳健性。