支持隐私保护的可验证云端数据分享方案

张晓均，刘 庆，郑 爽，王 鑫，薛婧婷，王世雄

（1.西南石油大学 计算机科学学院 网络空间安全研究中心，成都 610500；2.军事科学院，北京 100091）

0 概述

随着移动互联网行业的飞速发展，用户需要存储的数据量呈爆炸式增长，为降低本地数据的管理成本，将数据外包到云已成为普遍趋势［1-3］。由于数据对云及访问云存储的用户是可见的，因此也给用户带来了数据隐私和安全等重要问题［4-6］。为防止云用户敏感数据的泄露，在外包之前需要对数据进行加密，然而加密会破坏数据的原始结构，这将限制对加密数据进行特定检索的灵活性［7］，难以满足移动智能终端应用的轻量级要求。为保证云上密文数据的有效共享，提高数据检索精度和效率，亟须设计一种既能保证数据隐私又能提高检索正确性的可搜索加密数据共享方案。

现有的可搜索加密技术分为对称可搜索加密（SSE）和公钥可搜索加密（SPKE）两类。在SSE 方案中，数据发送方和数据接收方通过共享同一个密钥对密文文件之间关联的关键词和搜索陷门进行加密并执行加密查询。最早的SSE 方案由SONG 等［8］提出，其采用顺序扫描的方式进行关键词匹配，搜索时间与文档长度呈线性关系。近年来，一些可以保证前后向安全性［9-10］、防止文件注入攻击［11］等满足更高安全性的SSE 方案相继被提出，但也在存储空间和计算复杂度上有了更大的开销。SPKE 方案使用数据接收方的私钥生成搜索陷门和使用对应的公钥生成加密文件的关键词密文来进行加密查询。最早的SPKE 方案由BONEH 等［12］提出，即支持单关键字搜索的公钥加密方案（PEKS）。在PEKS 中，用户需要通过安全信道将陷门传到云服务器进行匹配搜索，安全性和效率还有待提高。随后，文献［13］结合SM9 密码算法构造了基于身份的可搜索加密方案，使用系统参数相对较小的非对称双线性运算提高了计算速度和安全效率，但无法使用户之间的身份得到验证。文献［14］提出一种适用于移动设备的轻量级公钥认证加密方案，该方案允许对手自适应选择攻击目标，但没有对服务器返回的密文数据进行完整性校验。文献［15］提出一种支持隐私保护的可搜索加密方案，其可对基于属性的加密数据提供关键字搜索，并具有隐藏的访问策略，但搜索计算开销与系统中存在的属性数量成线性关系。文献［16］设计了一种用于IIoT 环境的无证书可搜索公钥加密方案，但该方案存在离线关键词猜测攻击的风险［17］。

SPKE 自提出以来在许多场景中得到了成功应用，如加密数据过滤［18］、物联网数据保护［19］等。然而，虽然SPKE 在安全性、密钥管理和数据共享的灵活性方面较SSE 有一定优势，但部署到云上时容易受到各种攻击，如关键词猜测攻击（KGA）。离线的KGA 可分为外部攻击者在云服务管理之外发起的KGA 和云服务管理内部攻击者发起的内部KGA［20］。目前，研究者［21-23］已经提出了一些抵抗外部KGA 的方案，一类在接收者和云服务器之间建立一条安全信道，另一类是限制未经授权的攻击者进行测试。与抵抗外部KGA 相比，抵抗内部KGA 会更加困难，因为用于关键词测试的云服务器是“诚实而好奇”的，它可以在正常运行测试算法并返回给用户的同时猜测出关键词，内部攻击者很难被发现。因此，设计一种实用有效的方案来解决SPKE 中的内部/外部KGA 问题是一项具有挑战的任务。

本文提出一种云存储系统中支持隐私保护的可验证数据分享方案DSS-SPP-CSS。结合椭圆曲线上的加密算法和消息认证码技术设计关键词索引生成算法和搜索陷门生成算法，同时设计具有同态特性的密文数据签名生成算法，验证用户所接收加密数据的完整性。在此基础上，根据可证明安全理论，验证本文方案在选择关键词攻击下满足密文不可区分性和搜索陷门不可区分性。

1 系统模型与工作流程

1.1 系统模型

本文方案系统模型如图1 所示，其由可信中心、云服务器、数据发送方、数据接收方等4个不同的实体组成。

图1 本文方案系统模型Fig.1 System model of the proposed scheme

1）可信中心：可信的权威认证机构，主要负责设置系统的公共参数。

2）数据发送方：作为数据拥有者，在数据外包至云服务器之前对数据及其关键词进行加密，同时产生加密文件对应的文件名和同态数字签名，共同上传至云服务器进行存储。

3）数据接收方：作为数据使用者，根据搜索的关键词生成搜索陷门，将其发送至云服务器进行检索，并根据云服务器返回的检索结果验证密文数据的完整性。

4）云服务器：云服务器存储数据发送方上传的关键词索引、数据文件密文及其文件名和数字签名，并为数据接收方提供基于关键词的密文搜索服务。当数据接收方向云服务器发送搜索陷门时，它会快速执行搜索与测试并返回对应的加密文件给数据接收方；同时，为确保云存储密文数据的完整性，云服务器基于数据接收方的挑战信息，产生完整性验证证明信息并返回给数据接收方。

1.2 工作流程

本文方案工作流程如图2 所示，其中包括系统初始化、密钥生成、加密与签名产生、搜索陷门生成、云服务器搜索测试、完整性验证等6 个步骤。

图2 本文方案工作流程Fig.2 Workflow of the proposed scheme

1）系统初始化（SystemInit）：可信中心以安全参数λ为输入，设置基于椭圆曲线的循环群的相关参数、抗碰撞哈希函数，并选择消息认证码等系统参数，将以上参数作为全局参数Ω公开。

2）密钥生成（KeyGen）：以全局参数Ω作为输入，数据发送方和数据接收方分别计算对应的公私钥对（vs，qs）和(vr，qr)。

3）加密与签名产生（Encrypt-Sign）：数据发送方选择通用的加密算法生成加密文件集合Λ={c1，c2，…，cm}，并产生加密文件对应的文件名Δ={N1，N2，…，Nm}和同态签名集合Σ={σ1，σ2，…，σm}，然后以全局参数Ω、数据发送方私钥vs、数据接收方公钥qr和关键词ω作为输入，输出关键词对应的密文C，最后将(Λ，D，Σ，C)上传至云服务器进行存储。

4）搜索陷门生成（Trapdoor）：以全局参数Ω、数据接收方私钥vr、数据发送方公钥qs和关键词ω'作为输入，数据接收方输出与关键词关联的搜索陷门Tω'，并产生完整性验证挑战信息，上传至云服务器进行搜索。

5）云服务器搜索测试（Test）：云服务器根据全局参数Ω、关键词密文C和搜索陷门Tω'进行搜索测试，若搜索陷门与关键词密文匹配成功，则返回对应的数据加密文件，并根据挑战信息产生完整性验证证明信息，发送给数据接收方。

6）完整性验证（Verify）：完整性验证是为了防止云服务提供商返回不诚实的反馈信息同时减少用户的本地计算开销，在数据接收方接收数据之前根据云服务器返回的完整性验证证明信息对加密文件的搜索结果进行完整性验证。此步骤以全局参数Ω为输入，云服务器基于数据接收方的挑战信息chal、加密文件ci和对应的文件名Ni以及同态签名(σi，Ri)产生完整性验证证明信息(c，N，σ，R)返回给数据接收方，用于对云端加密数据的完整性验证。

2 方案设计

本文方案中包含系统初始化（SystemInit）、密钥生成（KeyGen）、加密与签名产生（Encrypt-Sign）、搜索陷门生成（Trapdoor）、云服务器搜索测试（Test）、完整性验证测试（Verify）等6 个多项式时间算法。

1）系统初始化（SystemInit）算法：首先选取一个安全参数λ作为输入，然后按以下步骤生成全局系统参数。

3）加密与签名产生（Encrypt-Sign）算法：在此算法中，数据发送方需要提取原始数据文件的关键词，并产生对应的关键词密文，同时数据发送方需要生成原始文件密文及其对应的同态数字签名。

最后，数据发送方将每一个数据文件fi，i=1，2，…，m对应的加密数据文件ci、关键词密文C以及加密文件的同态数字签名(σi，Ri)一起发送给云服务器。

4）搜索陷门生成（Trapdoor）算法：数据接收方选取目标关键词ω'，利用自身私钥vr=(vr，1，vr，2)及数据发送方的公钥分量qs，1计算关键词的搜索陷门Tω'=·MACd*(ω')，其 中d*=H1(xr·qs，1)，并将搜 索陷门Tω'发送给云服务器。

5）云服务器搜索测试（Test）算法：云服务器收到搜索陷门Tω'后，逐一对存储的关键词密文进行搜索测试，判断方程H(Tω'·C1)=C2是否成立，若测试方程成立，则匹配成功，返回对应的加密数据文件给数据接收方。

6）完整性验证（Verify）算法：不失一般性，这里假设同一个关键词匹配成功的加密数据文件有n个，分别为c1，c2，…，cn。为了确保这些密文是正确存储在云服务器端的，数据接收方需要进行完整性验证。

（3）数据接收方在接收到云服务器返回的完整性证明响应信息后，检验以下完整性验证方程是否成立：σ·P=？qs，1·N+c·qs，2+R·u。若等式成立，表明数据接收方成功搜索的加密数据文件未遭到破坏，云服务器存储的密文数据是完整的；否则，验证不通过，表明数据发送方存储在云服务器的加密数据文件的完整性遭到了破坏，数据接收方可以拒绝接收这些密文文件。

3 正确性证明

对本文方案进行正确性证明。假设ω为关键词密文中关键词的标识符，ω'为关键词搜索陷门中关键词的标识符，推导过程具体如下：

后续推导过程分以下2 种情况考虑：

1）如果是正确的数据发送方和正确的数据接收方，那么就可以得到d=d*，若式（1）的计算结果为不相等，则可判定数据发送方和数据接收方不匹配。因此，这一部分的设计可以有效检测出外部恶意敌手想冒充合法用户的情况。

2）当第1）种情况为式（1）的正确计算结果时，若关键词ω=ω'，则推导等式H(Tω'·C1)=C2成立，即关键词密文和搜索陷门匹配成功；但若关键词ω和ω'不相等，由于选取的是抗碰撞哈希函数，因此不难得出等式不成立的结果，保证了关键词匹配的正确性。

若云服务器返回给数据接收方的云端密文数据未被篡改，则式（3）成立，即表明数据完整性验证通过。

综合以上两种情况的推导，可以证明本文方案是正确的。

4 安全性分析

对本文方案进行安全性分析与证明。

定理1本文方案在选择关键词攻击下满足密文不可区分性。

证明：假设A1是针对所提出的选择关键词攻击下满足密文不可区分性（CIND-CKA）游戏的多项式时间攻击者，AH是抗碰撞哈希函数的攻击者，AECDLP是求解基于椭圆曲线离散对数困难问题（ECDLP）的攻击者。

由5 个游戏Gamei，i=1，2，…，5 作为子游戏程序，且以A1作为攻击者完成证明。本文将攻击者A1在Gamei中正确猜测的事件定义为Xi，即b=bi。攻击者将以最终输出终止，然后将对其进行评估，以查看攻击者是否“赢”。具体描述如下：

游戏1该游戏为原始敌手游戏CIND-CKA，因此，A1正确猜测的概率为：Adv(λ)A1=|Pr[X1]-1/2|。

游戏2该游戏与游戏1 相同，不同之处在于挑战者 B 选 择a，vr，1，vr，2∈来计算P'=a·P和qr=(qr，1，qr，2)=(vr，1·P，a·vr，2·P)，其中点P是群G的生成元，其他参数与游戏1 相同。由于游戏1 的参数与游戏2 的分布相同，显然，游戏2 与游戏1 对A1来说是无法区分的，因此A1在这两个游戏中猜测的概率相同，即Pr[X2]=Pr[X1]。

游戏3该游戏与游戏2 相同，不同之处在于B 更改了他/她响应A1密文查询、搜索陷门查询、测试查询以及挑战应答的方式，如下所述：

在上述游戏中，如果B 能够正确应答各种预言查询并完成挑战，那么对A1而言，游戏2 和游戏3 将是难以区分的。因此，攻击者A1在游戏2 和游戏3 中正确猜测的概率相同，即Pr[X3]=Pr[X2]。

游戏4该游戏与游戏3 相同，在以下任何事件发生时，B 都将终止游戏：

显然，除非事件E1∨E2发生，否则游戏3 和游戏4对于攻击者来说是无法区分的。根据文献［24］中的差分引理可以得出|Pr[X3]-Pr[X4] |≤Pr[E1∨E2]。

如果发生E1，则必须有一个针对哈希函数H的抗碰撞性的攻击者AH，即破坏哈希函数的抗碰撞性的攻击者，因此，若Adv(λ)AH≥Pr[E1]，则AH具有获胜的优势。同样，如果发生E2，则必须有一个针对消息认证码MAC 的抗碰撞性的攻击者AMAC，即破坏消息认证码的抗碰撞性的攻击者。因此，若Adv(λ)AMAC≥Pr[E2]，则AMAC具有获胜的优势。由此可得|Pr[X3]-Pr[X4]| ≤Pr[E1∨E2]≤Adv(λ)AMAC+Adv(λ)AH。

分析A1的优势，有：

根据以上游戏，可以得出以下结论：

由于哈希函数H和消息认证码的抗碰撞性，以及ECDLP 问题是困难的，因 此Adv(λ)AMAC、Adv(λ)AH和Adv(λ)AECDLP是可以忽略的，由此可以证明本文方案在满足选择关键词攻击下是密文不可区分的。

定理2本文方案在选择关键词攻击下满足搜索陷门不可区分性。

证明：假设A2是针对所提出的在选择关键词攻击下满足搜索陷门不可区分性（TIND-CKA）游戏的多项式时间攻击者，AH是抗碰撞哈希函数攻击者，ACDH是求解计算型Diffie-Hellman（CDH）困难问题的攻击者。

由攻击者A2的5 个游戏Gamei，i=1，2，…，5 作为子游戏程序。这里将Xi定义为攻击者A2猜测Gamei中的正确事件，即b=bi。攻击者将以一些最终输出终止，然后将对其进行评估，以查看攻击者是否“赢”。具体描述如下：

游戏1该游戏为原始敌手游戏TIND-CKA，因此，攻击者A2正确猜测的概率为Adv(λ)A2=|Pr[X1]-1/2|。

游戏2B 随机选择a，b，vr，2∈来计算qs，1=b·P和qr=(a·P，vr，2·P)，其中P是群G的生成元，其他参数与游戏1 相同。显然，游戏1 和游戏2 于A2是无法区分的。因此，A2在这两个游戏中正确猜测的概率相等，即Pr[X1]=Pr[X2]。

游戏3该游戏与游戏2 相同，不同之处在于B 更改了他/她对A2进行密文查询、搜索陷门查询、测试查询和质询的响应方式，如下所示：

1）密文查询：A2使用关键词ω∈KSω进行密文查询，B 选择随机数t∈并返回关键词密文C=(C1，C2)给A2，其中C1=t·qr，2，C2=H(t·MACd(ω)·P)，d=H1(b·a·P)。

2）搜索陷门查询：A2使用关键词进行搜索陷门查询，B 返回搜索陷门Tω'=(vr，2)-1·MACd*(ω')，其中，ω'∈KSω，d*=H1(a·qs，1)=H1(a·b·P)。

3）测试查询：A2使用关键词密文C和关键词搜索陷门Tω'进行测试查询，若H（Tω'·C1）=C2，则B 返回1，否则返回0。

4）挑战：A2发送2 个他/她之前从未挑战过的关键词ω0和ω1给B，其中ω0≠ω1，B 计算关键词搜索陷门Tωb'=（vr，2）-1·MACd*()，其中，b∈{0，1}，d*=H1(a·b·P)，然后将其返回给A2。

在上述游戏中，如果B 能够响应各种查询并正确挑战，那么游戏2 与游戏3 将于A2难以区分。因此，A2在游戏2 和游戏3 中猜测正确的概率相等，即Pr[X2]=Pr[X3]。

游戏4该游戏定义与定理1 证明中游戏4 相同，因此，存在抗碰撞的敌手A2的优势为|Pr[X3]-Pr[X4]| ≤Adv(λ)AMAC+Adv(λ)AH。

游戏5该游戏与游戏4 相同，不同之处在于B 在响应陷门挑战时选择一个点Z∈G来计算Tωb'=(vr，2)-1·MACd*(ω'b)中的d*=H1(Z)而不是d*=H1(a·b·P)。B 在游戏5 中仅使用CDH 元组(H1，P，a·P，b·P，Z)，而不需要知道a和b的值即可响应所有攻击者的查询和陷门挑战。显然，游戏4 和游戏5 是相同的，如果解决了CDH 问题，那么攻击者ACDH可以通过不可忽略的优势来区分a·b·P和Z的值。假设攻击者ACDH拥有赢得游戏5 的优势，则可得|Pr[X4]-Pr[X5] |≤Adv(λ)ACDH。

由于Z是群G的一个随机元素，因此A2正确猜测的可能性是Pr[X5]=1/2。

分析A2的优势，有：

根据上述游戏，可以得出以下结论：

由于Adv(λ)AH、Adv(λ)AMAC和Adv(λ)ACDH是可以忽略的，因此可以证明本文方案满足选择关键词攻击情况下是陷门不可区分的。

定理3支持隐私保护的可验证云端数据分享方案可确保云端密文数据的存储正确性。

证明：本文方案在数据发送方上传加密文件的同时，为每一份密文文件生成了一个同态数字签名(σi，Ri)用于进行搜索结果的完整性验证，其中σi=xsH2(Ni)+ysci+kiu∈。该签名基于改进的BLS 短签名算法设计完成，使用数据发送方的签名私钥vs=(vs，1，vs，2)对用户的数据密文进行签名，由于签名私钥只有数据发送方拥有，因此只有数据发送方才可以产生正确的签名，从而通过完整性验证，而非数据发送方的攻击者（如恶意云服务器）若想伪造签名，困难程度可归约到求解椭圆曲线上的离散对数困难问题。显然，成功伪造签名的概率是可以忽略的，恶意云服务器试图通过伪造数字签名产生伪造的完整性验证，证明信息达到欺骗用户的目的是计算不可行的。因此，本文方案可确保云端密文数据的存储正确性。

5 性能分析

将本文方案（DSS-SPP-CSS）与其他同样用于云端密文数据分享的公钥可搜索加密方案进行效率对比，包括PEKS［12］、PAEKS［25］、dIBAEKS［26］和CLEKS［27］。首先对各个方案的功能和特性进行对比，如表1 所示。比较结果显示，DSS-SPP-CSS 方案能够抵抗内部关键词猜测攻击，而且能够确保搜索的密文数据是正确存储在云服务器的。

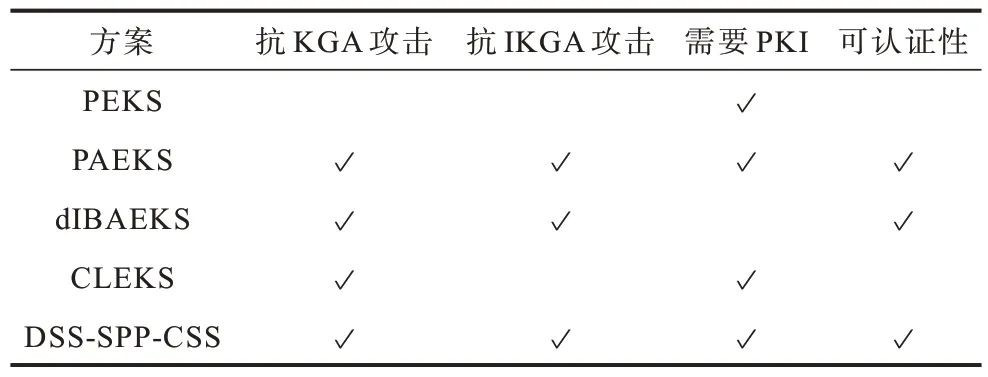
表1 不同方案的功能特征对比Table 1 Functional features comparison of different schemes

所有方案实现都运行在硬件环境为Intel Corei5 CPU 和8 GB DDR3 以及软件环境为Windows 10操作系统的笔记本电脑上。本文使用C 语言编写实验模型，主要用的库为PBC 库。实验使用到的椭圆曲线构造在Fp上，方程为y2=x3+x。群G中元素的比特长度为512 bit，q的比特长度为320 bit。

本文侧重于公钥可搜索加密功能对以上方案进行计算开销评估，主要由关键词密文生成计算开销、搜索陷门生成计算开销和测试算法计算开销等3 部分组成。相关运算符号含义如表2 所示。

表2 运算符号Table 2 Operational symbols

不同方案各个阶段的计算开销比较见表3。对各方案的计算效率作进一步分析与比较，如图3～图5 所示。可以看出，DSS-SPP-CSS 方案在关键词密文生成、搜索陷门生成、测试算法计算开销上都有着明显的性能优势，除了拥有密文数据分享功能外，其能有效抵抗内部云服务器关键词猜测攻击。此外，本文方案还具备完整性验证功能，当用户检索到密文文件后，会先对这些文件进行完整性验证，并在验证通过后进行密文文件的下载，从而有效保障云端加密文件的完整性，避免用户产生无效开销。

表3 不同方案各阶段计算开销对比Table 3 Computation overhead comparison in each stage of different schemes

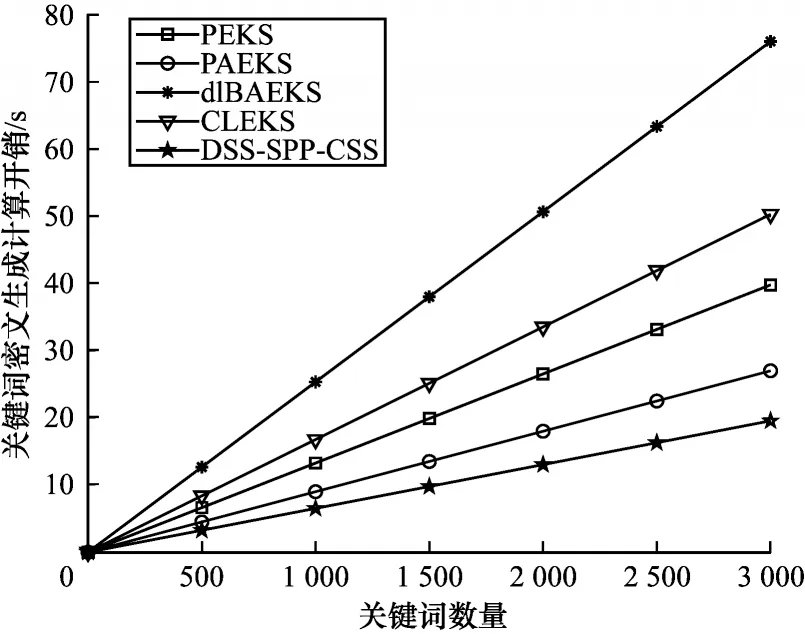
图3 关键词密文生成计算开销Fig.3 Computation overhead of keywords ciphertext generation

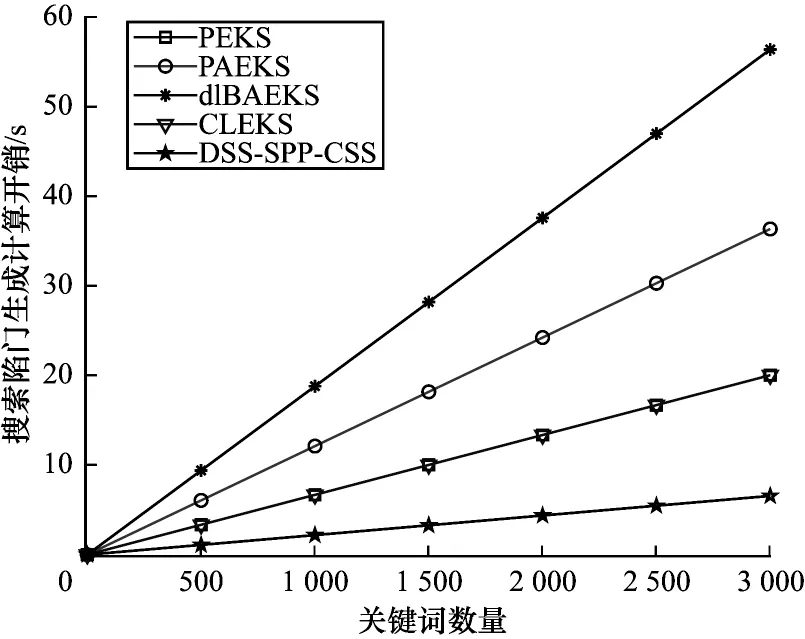
图4 搜索陷门生成计算开销Fig.4 Computation overhead of search trapdoor generation

图5 测试算法计算开销Fig.5 Computation overhead of test algorithm

从关键词密文长度和搜索陷门长度两个方面对比DSS-SPP-CSS 方案与其他方案的通信开销。设置本文方案中哈希函数H1和哈希函数H2的映射值的长度为320 bit（文中用ℓ1表示），其余方案的群中元素的长度与本文方案统一。不同方案的通信开销如表4 所示，其中，LG代表群中元素的位长，Lq代表q的位长。图6 给出了更直观的通信开销比较。可以看出：DSS-SPP-CSS 方案在关键词密文的通信开销上优于dIBAEKS、CLEKS 和PAEKS 方案，与PEKS 方案持平；在搜索陷门的通信开销上，优于PAEKS、CLEKS 和PEKS 方案，远低于dIBAEKS 方案。由此可见，与对比方案相比，DSS-SPP-CSS 通信开销更小，有助于减小端到端的延迟。

表4 不同方案的通信开销对比Table 4 Communication overhead comparison of different schemes 单位：bit

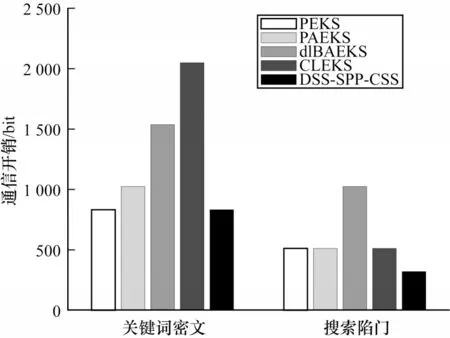
图6 各阶段通信开销Fig.6 Communication overhead in each stage

综上所述，本文提出的DSS-SPP-CSS 方案具有轻量级的性能优势，适用于面向云存储系统的移动终端应用场景。

6 结束语

面向云端数据保密分享需求，本文提出基于椭圆曲线的公钥可搜索加密方案DSS-SPP-CSS。该方案在选择关键词攻击下满足密文不可区分性和搜索陷门不可区分性，在随机预言机模型下可以抵抗内部关键词猜测攻击。性能分析结果表明，本文方案可以高效部署在云端加密数据分享应用场景，具有轻量级的性能优势。下一步将设计基于模糊关键词的可验证公钥可搜索加密算法，实现更灵活的数据保密分享功能。