膛内积水对火炮发射相关参量的影响模式

潘成龙， 蔡宣明， 侯 阳， 马沛冉， 曹晋伟， 王吕昊

(中北大学 航空宇航学院， 山西 太原 030051)

0 引 言

现代战争要求火炮具备较高的综合性能， 不仅要达到高初速、 大威力的作战要求， 还需要考虑火炮对恶劣环境的适应性。 火炮发射过程中因外部恶劣环境所引起的膛压增大或减小都有可能影响火炮发射过程的安全性与射击精度。 因此， 火炮对不同作战环境的适应性是火炮综合性能的重要指标之一。 雨雪天气是火炮面临的恶劣环境条件之一， 在恶劣的雨雪天气条件下发射炮弹， 身管内的积水对弹丸速度和药室压力的影响是一项重要的研究内容， 探究火炮发射过程中膛内积水对火炮安全性与射击精度的影响具有重要的意义。

目前， 由于膛内积水对弹丸发射时的影响的相关研究并不深入， 因此很难在理论上建立膛内积水条件下弹丸发射过程的数学模型。 数值模拟仿真可以用来研究弹丸发射的内弹道性能， 许多学者对此开展了研究。 冯勇等[1]通过建立某高速弹丸发射的力学仿真模型， 验证了该火炮弹丸发射的仿真计算结果与实弹试验结果基本吻合。 叶辛等[2]对数值仿真与理论计算所得到的高速弹丸发射过程中弹丸的受力情况进行了对比， 结果表明， 数值仿真能较好地反映弹丸的受力情况。 李淼等[3]通过对某大口径火炮弹带热力耦合挤进动力学的数值模拟研究发现， 弹带间隙与弹丸的攻角对弹丸的挤进过程有着重要的影响。 张跃跃等[4]通过改变发射药的燃烧环境来分析膛压变化对弹丸发射过程的影响， 证实了内弹道过程中发射药燃烧环境的变化是影响弹丸发射过程的关键因素。 李庚等[5]通过对比仿真分析与试验得到的某高速动能弹丸发射时弹丸的受力情况证明了仿真分析结果的正确性， 并通过仿真得到了弹丸横向过载与弹丸质量偏心距有关的结论。 周家胜等[6]通过测试膛内加速度的过载情况以及全弹结构强度的仿真分析， 得知炮口出现的测试曲线高频阶跃现象是弹体前端与火炮身管内壁的碰撞造成的。 李庚等[7-8]通过建立弹丸发射系统动力学模型， 明确了弹丸在内弹道中的运动和受力特征， 并对弹丸发射安全性进行了评估。 王惠源等[9]通过分析弹丸的内弹道运动过程， 得出弹丸的攻角对射击精度有影响的结论。 以上学者主要是对火炮发射的可靠性以及稳定性进行了研究， 对在雨雪环境下膛内积水对火炮发射的影响还缺乏较为系统的研究。

本文基于SolidWorks构建空气-积水-发射药-药室-身管-弹丸耦合的三维模型， 利用Hypermesh软件对三维模型进行网格划分， 并利用LS-DYNA软件进行有限元计算， 分析在火炮发射过程中药室内压力的特性， 研究在不同的膛内积水量条件下弹丸的速度以及弹丸所受压力的变化规律， 进而揭示膛内积水对火炮发射的影响规律。

1 仿真分析假设与建模

1.1 基本假设

为简化仿真计算难度， 作出如下假设：

1) 假定身管、 药室以及弹丸均为刚体。

2) 忽略弹带， 让弹丸直接与身管接触， 密闭且不计摩擦。

3) 假定身管中的水以圆柱体的形式存留在身管中。

1.2 有限元模型

为了研究火炮发射时膛内积水对弹丸以及药室的影响， 首先以火炮在单纯空气环境下发射作为基础模型， 进行仿真模拟计算。

为了加快收敛速度， 节约计算时间， 空气域、 水域、 药室、 身管以及弹丸5个部件的网格均采用六面体网格。 计算模型分为空气域、 水域、 发射药(在LS-DYNA软件中根据坐标系来进行定义)、 药室、 身管以及弹丸6个部分。 因为身管为圆柱形， 为了方便计算把身管内积水的形状简化为圆柱形， 又因需要对水域和空气域的网格进行共节点(防止空气域与水域之间的压力不能正常地传递)， 所以把空气域也建为圆柱形。 空气域的直径为287 mm， 长度为 5 000 mm， 网格采用渐变网格划分， 从炮管轴线开始划分， 单元尺寸从2 mm 增大到8 mm， 划分为370万个单元； 水域的直径为155 mm， 厚度分别为0 mm, 8 mm, 16 mm, 24 mm和128 mm， 网格尺寸为2 mm； 火药药柱以填充的形式置于药室内， 药室的内径为155 mm， 长度为180 mm， 壁厚为40 mm， 网格尺寸为4 mm, 有限元模型如图1 所示； 身管的内径为155 mm， 长度为4 000 mm， 壁厚为40 mm， 网格尺寸为4 mm； 弹丸的直径为155 mm， 长径比为7， 头部形状系数CRH为2.8， 质量为20 kg, 网格尺寸为2 mm， 弹丸模型如图2 所示。 在仿真计算时， 药室、 身管和弹丸的材料模型均采用刚体。

图1 药室有限元模型

(a) 弹丸剖视图

在火炮发射过程中， 身管、 药室以及弹丸完全处于空气域中， 弹丸发射是在药室内发射药所产生的高温高压燃气的作用下完成的。 根据流体与固体相互作用的特点， 在有限元计算时采用多物质流固耦合算法[10]。 药室-身管-弹丸结构采用Lagrange单元网格， 其中药室与身管共节点刚性连接； 药室和身管内外部的空气和积水建立在同一流体域中， 其中药体、 空气和水采用ALE单元网格。 为了防止药室内产生的冲击波在空气域边界发生冲击波反射现象， 在空气域边界施加使压力流出边界的条件模拟无限空气域， 设置空气压强为1.0×105Pa。 如图3 所示， 为了分析在火炮发射时药室内高温高压燃气的载荷特性， 在药室内壁设置4个监测点来记录药室内的压力载荷。 爆炸中心与监测点的夹角与距离见表1， 本研究在进行有限元模拟时采用 mm-g-s单位制。

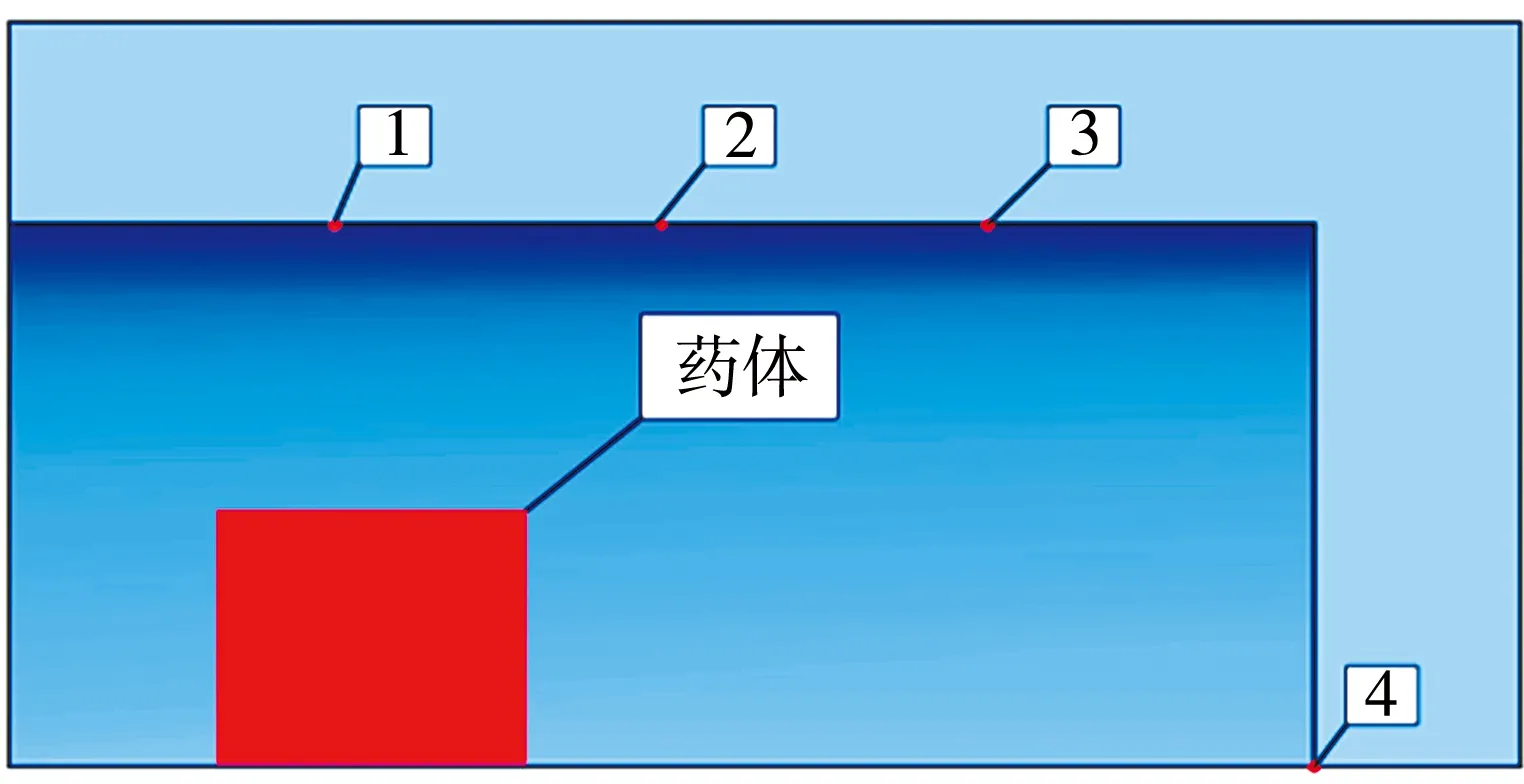
图3 药室压力监测点示意图

表1 爆炸中心与监测点的夹角与距离

1.3 材料模型

1.3.1 空气

采用理想气体状态方程对空气的材料本构关系进行描述， 表达式为

pA=(γ-1)ρAeA+pshift,

(1)

式中：pshift为空气的初始压力， 取1×105Pa；eA为气体的内能，eA=206.8 kJ/kg；γ为空气在理想状态下的绝热指数，γ=1.4；ρA为空气的密度，ρA=1.293×10-6g/mm3。

1.3.2 发射药

采用JWL状态方程对高能发射药模型所产生的燃烧产物进行描述， 表达式为

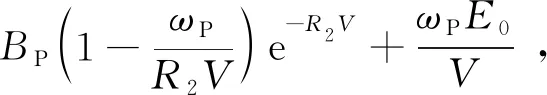
(2)

式中：pP为燃烧产物的压力；AP,BP,R1,R2,ωP为发射药的材料参数；E0为单位体积发射药的初始能量；V为发射药的相对体积。

1.3.3 水

水的材料本构关系通过Polynominal状态方程来描述， 当水压缩时(μ>0)， 状态方程为

pW=A1μ+A2μ2+A3μ3+(B0+B1μ)p0eW，

(3)

当水膨胀时(μ<0)， 状态方程为

pW=C1μ+C2μ2+B0p0eW，

(4)

式中：pW为水的压力；p0为水的初始压力；μ为水的压缩比，μ=ρ/ρ0-1；eW为水的内能，eW=289.5 kJ/kg；ρ0为水的密度，ρ0=1×10-3g/ mm3；A1,A2,A3,B0,B1,C1,C2均为水的材料参数，A1=C1=2.2×109Pa；A2=9.54×109Pa；A3=1.46×109Pa，B0=B1=0.28，C2=0。

2 仿真计算结果及分析

表2 为5种工况膛内积水量的仿真计算结果， 图4～图8 为在膛内积水不同的情况下火炮发射时弹丸在膛内的压力云图。 由图4 得， 当膛内无积水时， 弹体在1.78 ms～2.58 ms之间所受载荷是逐渐增加的， 这是因为在1.78 ms～2.58 ms的时间内， 药室内的压力处于增大状态(见图9)； 由图4～图8 可知， 弹丸在膛内运动到2.18 ms与2.58 ms时， 弹丸所受最大压力随着膛内积水量的增大而增加， 由此可以得出在火炮发射时， 随着膛内积水的增加， 弹丸在膛内运动所受的压力增大； 由图5～图8 可知， 当膛内存有积水时， 弹丸从接触到积水到积水从弹丸获得能量与弹丸一同运动的过程中， 弹丸在膛内所受的最大压力先增加后减小。 这是由于当弹丸撞击到水时， 水的速度小于弹丸的速度， 水对弹丸产生一定的压力， 且积水越多压力越大。

表2 不同工况下膛内所对应的积水量

图4 工况1弹丸压力云图

图5 工况2弹丸压力云图

图6 工况3弹丸压力云图

图7 工况4弹丸压力云图

图8 工况5弹丸压力云图

以图3 所示的4个监测点为研究对象， 对药室内的压力进行分析， 各工况下药室内4个监测点处的压力-时间曲线如图9 所示。

(a) 监测点1

由图9 可知， 燃烧初期药室内压力先逐渐上升， 然后随着发射药燃烧面积的增加， 压力上升得越来越快， 直到达到峰值； 随后弹后空间逐渐增大， 膛内压力随着弹丸的运动不断下降。 5种工况在达到各自的压力峰值之前药室内爆载荷的大小基本相同。 监测点1和监测点2在达到峰值后压力开始随着膛内积水的增加而增大， 其中， 监测点1处的压力峰值增加1%～2%， 监测点2处的压力峰值增加2%～7%。 这是因为随着膛内积水的增加， 弹丸在高速运动中撞击积水后， 积水会以水膜的方式存在于弹丸与身管壁之间形成密封， 减少了药室压力的散失； 而在同一工况下， 监测点3处的压力峰值却不稳定， 这是由于监测点3的位置处于角隅处， 冲击波与反射波相互作用而导致的； 由监测点4的压力曲线可知， 工况2～工况5的压力峰值比工况1分别减少了0.41%, 6.18%, 9.05%, 19.75%， 由此可知药室底部的压力随着膛内积水的增加而减小， 这是由于弹丸在发射过程中高速撞击到膛内积水， 膛内积水会从弹丸获得一定的能量， 随着积水的增加， 弹丸损失的能量就越多， 弹底压力是火炮发射的驱动力， 它是促使弹丸在内弹道产生加速的主要因素[2]， 而弹底压力与膛底压力存在一定的相互作用关系， 所以弹底压力的变化会直接影响膛底压力的变化。

在火炮发射时， 药室内的起始燃烧中心到药室内壁上各监测点的距离以及药室内的冲击波到达各点的入射角均不同[10]， 导致药室内各监测点的压力有很大的差异。 不同工况下药室内4个监测点的最大压力见表3。

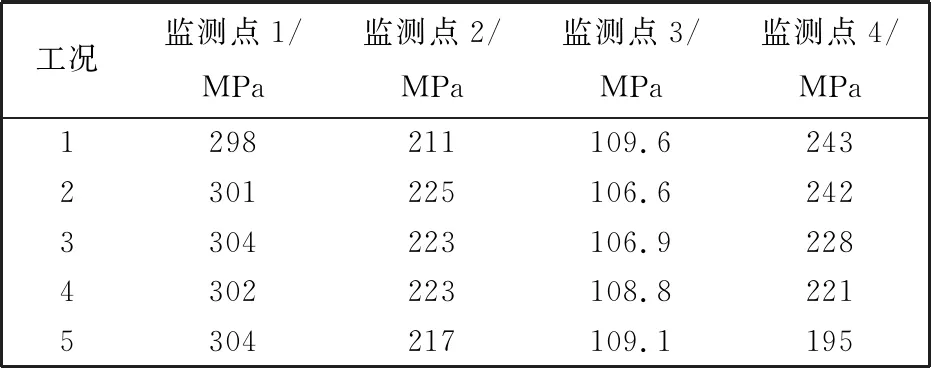
表3 不同工况下监测点处的最大压力

由表3 可知， 在同一工况下， 监测点1的压力最大值是监测点2的1.35倍， 是监测点3的2.7倍， 除工况5以外监测点1的压力最大值是监测点4的1.3倍； 在同一监测点不同工况下监测点的压力增加5%～7%。 结合各监测点与爆炸中心的夹角与距离(见表1)可知， 冲击波的入射角对药室内壁压力的影响大于距离对药室内壁压力的影响。 此外， 监测点2与监测点3有多个峰值， 这是因为从爆炸中心向药室角隅处传播的冲击波与药室内壁反射回来的反射波共同作用形成汇聚波， 因此在监测点2与监测点3处表现为多个峰值。

由图10 弹丸在膛内的加速度曲线可知， 当弹丸在膛内撞击到水后， 弹丸加速度的增加速度变小， 且随着膛内积水量的增加加速度减小； 随着膛内的积水量增加， 弹丸达到加速度峰值的时间逐渐增加， 这是因为膛内积水会起到一定的吸能作用； 当膛内存有大量积水时， 弹丸的加速度曲线出现多个峰值， 这是因为弹丸高速撞击积水后， 由于膛内积水过多， 积水对弹丸进行了多次冲击， 从而使弹丸的加速度曲线具有多个峰值。

图10 弹丸的加速度时间曲线

由图11 可知， 膛内存在积水时， 弹丸初始会以相同的速度运动， 当弹丸开始接触到积水后， 水的速度迅速上升并以与弹丸相同的速度在膛内运动， 根据动量守恒定律， 水会从弹体获得大量的能量， 从而使弹丸速度减小。 积水量越多弹丸损失的能量就会越多， 因此当弹丸在膛内高速撞击积水后速度先有微小的下降， 然后再逐渐上升， 但始终比无膛内积水状况下的低。

图11 弹丸的速度时间曲线

3 结 论

本文在其他条件相同的情况下， 对火炮膛内加入不同量的积水进行仿真计算与分析， 结果表明：

1) 火炮发射时， 当弹丸撞击到膛内的积水后， 积水水膜会在弹丸及身管壁产生一定的密封作用， 减少药室内能量的散失， 从而使火炮药室内侧壁压力上升5%～7%；

2) 弹丸在膛内高速撞击积水时， 积水会对弹丸产生一定的吸能作用， 通过吸收弹丸的能量来消耗弹底压力， 而弹底压力与膛底压力又相互关联， 因此膛底压力随着膛内积水的增加而减小；

3) 当膛内存有积水时进行火炮发射， 弹丸的速度与加速度随着膛内积水的增加而减小， 且弹丸达到最大加速度的时间会随着膛内积水的增加而延后。