基于改进灰狼优化算法的立体车库调度优化

陈 敏， 陈 晔， 许民宗， 郭晓宇

(中北大学 电气与控制工程学院， 山西 太原 030051)

0 引 言

由于巷道堆垛式立体车库车位多， 出入口少， 导致用户存取车等待时间较长， 降低了存取车的效率。 因此， 以存取车调度时间为模型对这类立体车库利用优化算法优化调度， 以提高车库运行效率， 减少存取车的等待时间具有重大意义[1]。

国内学者对立体车库存取车调度的研究已取得显著的成果， 使用的算法主要有遗传算法(GA)、 模拟退火算法(SA)、 粒子群算法(PSO)等。 魏丽[1]应用改进遗传算法并利用MATLAB遗传算法工具箱对巷道堆垛立体车库存取调度时间和能耗进行建模仿真， 得到了时间最优迭代曲线和最优操作序列， 最后将结果与随机分配策略的结果进行比较， 验证了改进遗传算法在提高车辆存取效率上的有效性。 陈桂兰等[2-3]使用改进粒子群算法对立体车库存取策略的时间模型进行仿真优化， 在粒子群算法的基础上引入了遗传算法和模拟退火算法， 提高了算法的全局搜索能力且避免其陷入局部最优解， 与传统的遗传算法相比， 改进后的算法存取效率提高了24.5%～36.0%。 李剑锋等[4]使用改进遗传算法对巷道堆垛立体车库的存取调度进行优化， 以总存取时间为模型建立了目标函数， 经过仿真试验后得到较小的存取车总时间以及存取车优化序列。 YIN等[5]引入学习强化算子和卡尔曼滤波对灰狼算法进行改进， 使用6个测试函数验证了改进后算法的寻优性能， 最后将其用于解决流水车间调度中的节能问题。 LI等[6]以满意度作为优化目标建立数学模型， 使用改进遗传算法得到了最优调度结果， 并将其与以客户等待时间为目标的优化结果相比较， 证明了满意度作为优化目标的有效性。

以上研究在对自动化立体车库进行调度优化时， 都只是对之前的算法进行改进， 没有再引入新的方法和思路对存取车调度进行研究。 灰狼优化算法是Mrijalili提出的一种智能优化算法， 具有原理简单、 易于实现、 需调整的参数少、 求解精度高、 收敛速度快、 在函数优化问题中优于其他智能算法等优点[7-8]。 虽已有学者使用此算法对流水车间的调度进行研究， 得到了较好的验证结果， 但目前灰狼优化算法在立体车库存取车调度的研究中鲜有应用。

本文使用改进的灰狼优化算法对车库调度问题进行研究。 根据立体车库车辆调度的特点， 使用遗传算法、 邻域搜索操作对灰狼算法进行改进： 引入遗传算法的交叉操作改进灰狼算法的位置更新公式； 为了解决灰狼算法易陷入局部最优解的缺点， 引入邻域策略对更新后种群中的领头狼进行局部搜索操作， 以获得更优的灰狼个体， 从而整体上带动种群向更优的方向更新。 研究结果与文献[4]中所使用的改进遗传算法作比较， 验证了算法在降低存取车时间上的有效性。

1 巷道堆垛立体车库概述

巷道堆垛式立体车库由旋转平台、 升降机、 堆垛机等组成。 本文的研究对象为单巷道两区车库， 每区有4层4列16个车位， 两区共有32个停车位。 1区的1层1列为转换层， 其结构如图1 所示。 该类车库的优势是利用堆垛机同时进行水平和垂直运动使车辆到达指定位置， 再由搬运器进行存取操作[9]， 极大地节省了存取车时间。 其车位平面分布如图2 所示。

图1 巷道堆垛式立体车库三维结构图

(a) 车库1区坐标

2 存取策略优化及建模

巷道堆垛式立体车库在接收到存车操作指令时， 升降机将待存车辆垂直运送到转换层， 由堆垛机将车辆运送到目的地； 当接收到取车操作指令时， 待取车辆通过堆垛机运送到转换层， 然后由升降机将车辆输送到出入口进行旋转等待出库。

在存取车的整个过程中， 升降机、 旋转台都是确定的， 它们的运行时间也是确定的， 但堆垛机的运行时间却不确定， 这主要是由于存取车时的车位不确定， 堆垛机空闲时的停靠位置不确定， 堆垛机行进路线不确定等原因造成的。 因此， 存取车位的分配、 堆垛机运行路径的规划以及堆垛机空闲时的停靠位置等是立体车库存取策略的主要研究内容。

立体车库存取策略主要包括存车优先策略、 取车优先策略、 交叉存取策略。 为了对比这3种策略下的调度时间， 本文对每一种策略都安排相同的出入库次数。

2.1 存车优先策略

将存取车任务进行分组， 先进行存车操作。 堆垛机完成存车操作后回到转换层待命， 当有下一次的存车任务到来时可以直接进行存车操作[10]。 这种存车策略适应于某一存入车辆较多时的时间段。 存车优先策略的数学模型为

(1)

式中： (a0,b0) 为转换层坐标； (a1,b1)为堆垛机执行上一步操作时的位置； (a2,b2)为堆垛机所要到达的目的地；t1为升降机运行一次所需的时间；t2为堆垛机在相邻两层间运行所需的时间；t3为堆垛机在相邻两列间运行所需的时间；t4为旋转台旋转一次所需的时间；n1为待存车数目；n2为待取车数目。

2.2 取车优先策略

当有存取操作时先进行取车操作， 每次完成取车操作后堆垛机都回到原取车地等待， 当下一次取车任务到来时堆垛机从原取车地直接到达待取车地。 完成存车操作后， 堆垛机在原地待命[10]。 这种存取策略适用于某一集中取车的时间段。 取车优先策略的数学模型为

2max{t2|a2-a0|,t3|b2-b0|}+t4)+

max{t2|a2-a0|,t3|b2-b0|})。

(2)

2.3 交叉存取策略

在某一时间段内既进行存车操作也进行取车操作， 存取车操作交叉进行， 堆垛机完成取车操作后待在转换层等待进行下一步的存车操作， 存车操作结束后堆垛机原地待命。 这种存取策略适用于普通的存取车时间段。 交叉存取策略的数学模型为

max{t2|a2-a0|,t3|b2-b0|}+t4+t1),

(3)

由太原某大厦调研数据可知， 堆垛机在相邻两层之间的运行时间为10 s， 在相邻两列间的运行时间为 5 s， 升降机升降一次所需时间为10 s， 旋转台进行一次旋转操作所需时间为5 s。 转换层的坐标为(1,1)。

3 改进灰狼优化算法

3.1 灰狼优化算法

灰狼优化算法(GWO)是以自然界中狼群的狩猎以及生活习性为基础的一种群智能优化算法[11]。 狼群有严格的等级制度， 每支狼群都可以分成4个等级层次， 如图3 所示。

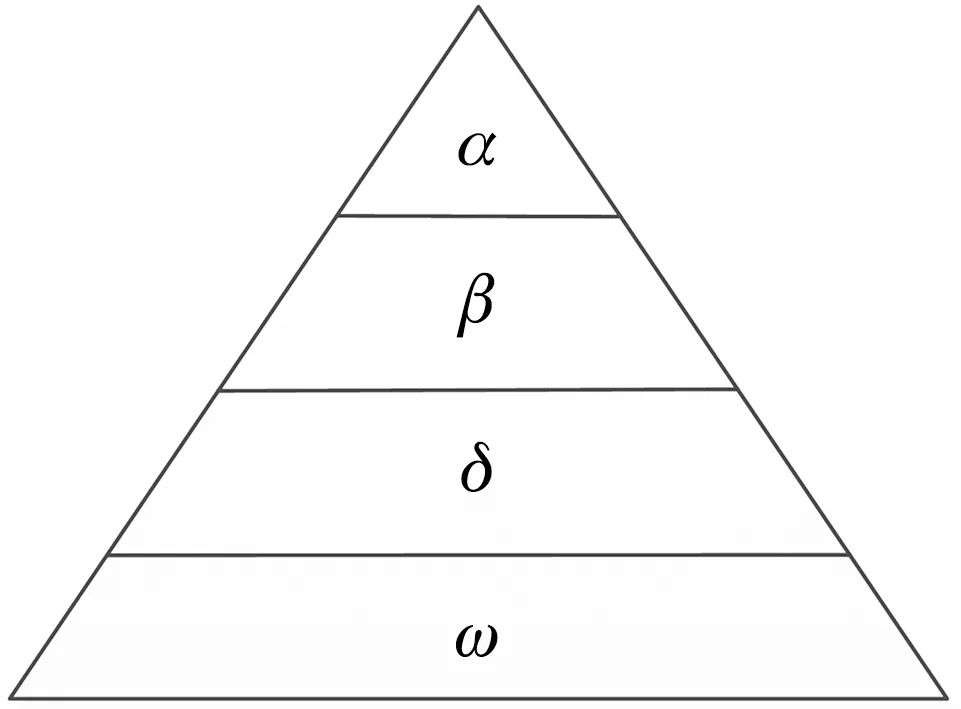
图3 狼群等级层次的划分

在GWO算法中， 由领头狼(α,β,δ)引导搜索， 而ω作为候选狼跟随前面的领头狼[12]。

3.1.1 包围猎物

灰狼从搜索区域内发起攻击， 将对猎物进行包围狩猎[8，13]， 包围行为的数学描述为

D=|C·Xp(k)-X(k)|,

(4)

X(k+1)=Xp(k)-A·D,

(5)

式中：k为当前迭代次数；A和C均为协同系数向量；D为种群个体与猎物之间的距离；Xp为猎物的位置向量；X为灰狼的位置向量。

向量A,C的计算公式为

A=2a·r1-a，

(6)

C=2·r2，

(7)

其中，a在迭代过程中从2线性减少到0， 即

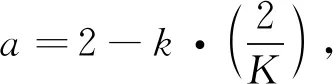
(8)

式中：r1,r2为[0,1]之间的随机向量；K为最大迭代次数。

3.1.2 狩猎

在整个狩猎的过程中都由头狼进行引导，β和δ狼有时也会进行狩猎。 灰狼个体的下一个位置是根据领头狼的位置来搜索和更新的[14]， 位置更新公式为

(9)

(10)

(11)

3.2 改进灰狼优化算法

1) 交叉操作式位置更新策略

立体车库存取车调度是一个离散优化问题， 而GWO优化的问题都是连续的， 显然使用式(9)～式(11)进行灰狼个体的更新是行不通的。 所以， 本文引入GA算法中的交叉操作对GWO算法中的位置更新策略进行改进。 以相同的概率选择α，β，δ狼与当前灰狼个体随机进行交叉操作， 位置更新公式为

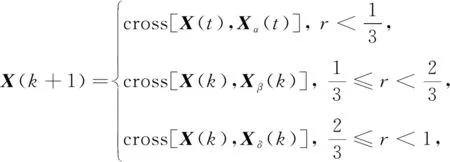
(12)

式中： cross表示两个个体进行交叉操作；r为[0,1]之间的随机数。

2) 邻域搜索局部寻优策略

领域搜索的主旨是对得到的某个局部解使用邻域操作对其周围个体进行搜索来获得最终解， 已被广泛应用于解决组合优化问题。 主要的邻域操作有交换操作、 插入操作、 逆转操作等。

在灰狼寻优过程中， 为了使领头狼带领种群向更优的位置更新， 本文引入邻域搜索对领头狼(α,β,δ)分别进行搜索操作， 以避免整支狼群进入局部最优状态。 为了进一步扩大搜索范围， 搜索到更多的解， 在获得邻域集合之前先对领头狼进行相同邻域操作的扰动操作得到“扰动解”， 然后使用该邻域操作获得这个“扰动解”的邻域集合， 在增加种群多样性的同时利于算法跳出局部最优。 根据立体车库调度的特点， 本文选择逆转操作， 主要理论及操作步骤详见文献[15]。

3.3 IGWO算法实现

使用IGWO算法解决立体车库的调度问题主要包括参数设定、 编码与解码、 初始种群的生成、 目标函数的确立、 种群个体位置更新和局部寻优。

3.3.1 编码与解码

本文采用2段混合编码方式进行编码操作， 结合车库存取车调度优化的实际情况， 其主要包含车位位置和存取操作两部分。 若总共有m辆车待存取， 其中有n1个为存车操作，n2个为取车操作，n1+n2=m， 则灰狼个体的总长度为2m。 前m个元素由实数组成， 表示待存取车位位置； 后m个元素由二进制(0,1)组成， 表示存取操作， 0代表取车操作， 1代表存车操作。 将车位位置与存取车操作进行一一对应， 部分编码如表1 所示。

表1 部分编码序列

3.3.2 种群初始化

对灰狼初始种群采用随机方法生成， 灰狼个体的前m个元素由1～m个整数随机排列组成， 后m个元素由n1个1和(m-n1)个0随机排列组成， 个体总长度为2m。

3.3.3 目标函数

本文的目标是求调度总时间的最小值。 所以， 目标函数Ft表示为

Ft=ti,i=c,q,j,

(13)

式中：ti表示各个策略下存取车所使用的总时间。

3.3.4 位置更新

在进行个体位置更新时， 灰狼个体与α,β,δ狼的交叉概率皆为1/3。 随机选择两个灰狼个体上的部分片段进行交叉操作， 并将交叉后个体上重复的元素删除。 如：

个体2： 5 4 3 2 1 0 1 0 1 1

若交叉片段为2～4， 将车位位置与存取车操作整体进行对应交换， 则将个体1和个体2上位置2～4的整数编码元素及其对应的3个0 1编码元素进行交叉操作， 即将2个个体的交叉片段相互交叉放置在另一个个体前端， 如：

个体2： 3 1 5543210 1 001011

最后将交叉后的个体中重复的元素删除， 更新后的个体1和个体2， 如：

个体2： 3 1 5 4 2 0 1 0 1 1

3.3.5 局部寻优

对上一步完成位置更新后种群中的α,β,δ狼实行局部寻优操作， 主要包括获得“扰动解”以及“扰动解”的邻域集合。

假设位置更新后个体α的编码为

1) 扰动操作为逆转位置3～5上的元素， 所得“扰动解”为

2) 引入逆转操作获得“扰动解”的邻域集合， 如逆转片段为2～4， 则

3.4 IGWO算法立体车库调度流程

IGWO算法求解立体车库调度问题的流程如图4 所示。

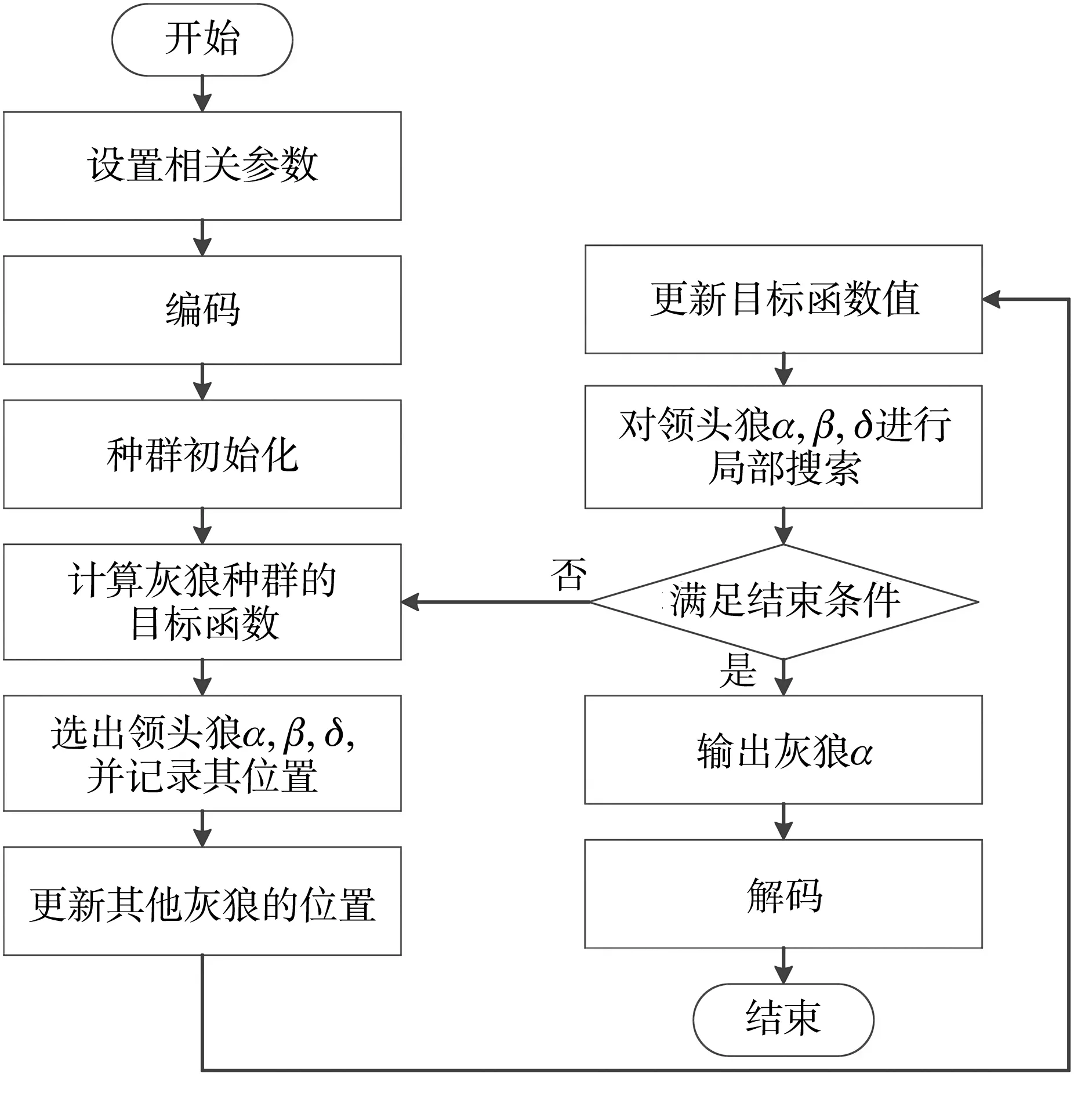
图4 IGWO求解车库调度流程图

4 结果与分析

4.1 改进灰狼优化算法参数设置

按照第2节中立体车库的存取调度时间模型， 并对第3节的改进灰狼算法进行设计， 可得出IGWO算法的部分参数， 如表2 所示。

表2 IGWO算法部分参数

4.2 实验结果与分析

为了验证IGWO算法对车库存取调度时间的影响， 将其与GWO以及文献[4]中的改进遗传算法(IGA)进行比较。 3种存取策略采用相同的存取次数。 该巷道堆垛式立体车库共有31个车位， 假设在某时段有21辆车待存入， 10辆车待取出， 目标函数为存取完全部车辆所需的总时间， 目标函数值越小代表算法效果越好。 实验环境为PC， 仿真软件为MATLAB R2020b， PC主机为Intel(R) Core(TM) i7-8700， 主频为 3.20 GHz， 内存为16 GB， 操作系统为Windows 10。

4.2.1 存车优先

存车优先仿真结果如图5 所示， 实验结果表明IGWO算法比GWO和IGA算法效果好。 IGWO算法在第100次迭代后得到的最短存取总时间为832 s， GWO与IGA分别在迭代110次和140次后才逐渐收敛， 最终结果分别为1 043 s和1 263 s。 由此可见， 本文所提出的IGWO算法整体收敛速度较快， 收敛效果更好， 减少了顾客存取车的等待时间。 IGWO算法的最优存取序列如表3 所示， 其中， 第1列的数字1和第32列的数字1为对应元素， 表示对1号车位进行存车操作； 第22列的数字17和第53列的数字0为对应元素， 表示对17号车位进行取车操作。 其他组数据依此类推。

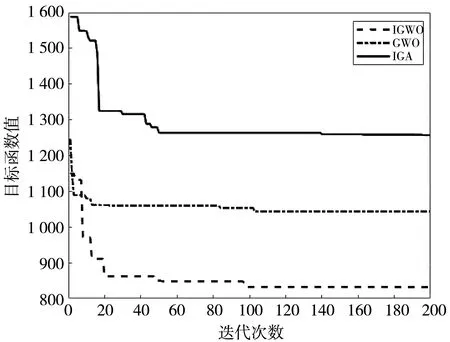
图5 存车优先算法对比

表3 存车优先策略存取车序列

4.2.2 取车优先

取车优先仿真结果如图6 所示， 使用IGWO算法得到的最短存取总时间为724 s。 最优存取序列如表4 所示， 按此存取序列在取车优先策略下进行存取操作可使总存取操作时间最短。

表4 取车优先策略存取车序列

图6 取车优先算法对比

4.2.3 交叉存取

交叉存取仿真结果如图7 所示， IGWO算法最终得到的最短存取总时间为540 s， 与IGA算法相比总存取时间减少了198 s， 与GWO算法相比减少了109 s。 最优存取序列如表5 所示。

表5 交叉存取策略存取车序列

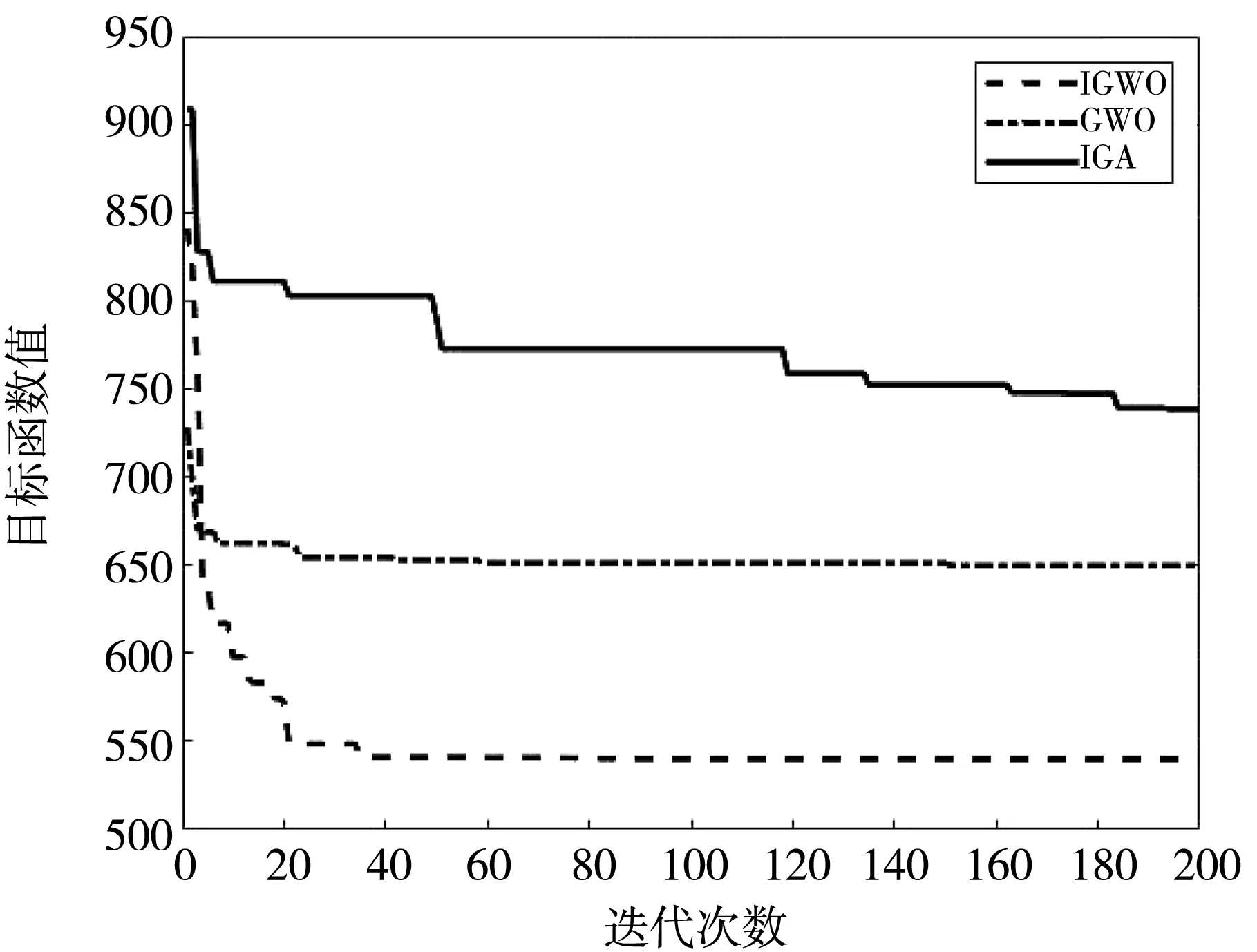
图7 交叉存取算法对比

表6 为IGWO算法、 GWO算法、 IGA算法在运行10次后总存取时间的平均值， 表7 为IGWO与其余两种算法总时间平均值的对比结果。 由表6、 表7 可知， 本文提出的IGWO算法在存取车调度时间上比GWO算法减少了18.8%～19.6%， 比IGA算法减少了31.1%～33.7%； 在3种存取策略中交叉存取策略所用的总时间最短， 在存取车数目相同时可优先选择交叉存取策略。

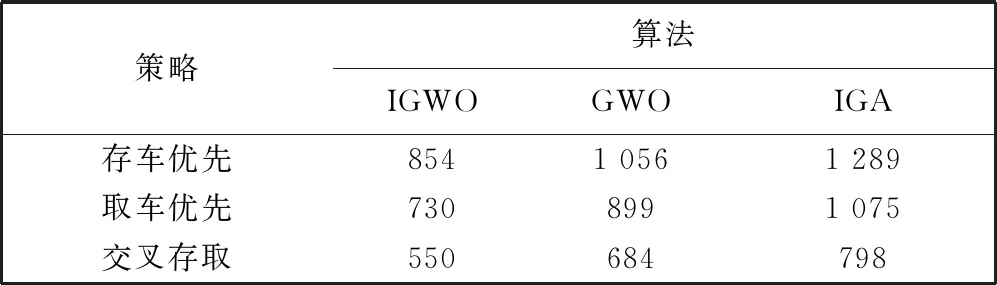
表6 IGWO， GWO， GA算法的总存取时间

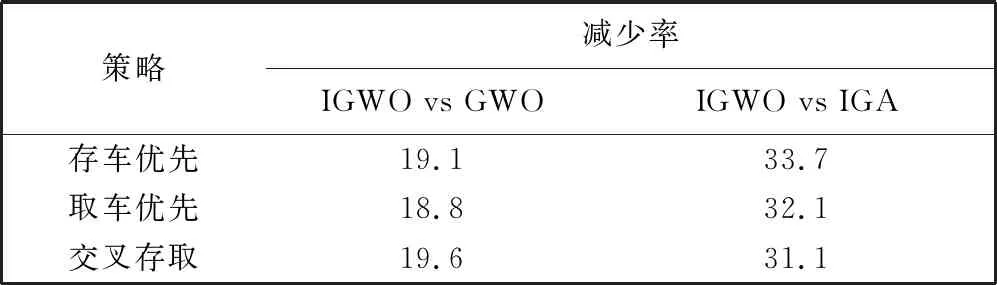
表7 IGWO与GWO， IGA算法的对比结果

5 结 论

本文使用IGWO算法对巷道堆垛式立体车库的存取调度进行了优化， 并通过仿真试验在存车优先、 取车优先、 交叉存取3种存取策略下与GWO算法、 IGA算法进行了比较。 从实验结果可以看出， IGWO算法比GWO算法的总存取时间减少了18.8%～19.6%， 比IGA算法的总存取时间较少了31.1%～33.7%。 本文所提出的IGWO算法提高了存取车效率以及车库效益， 为研究立体车库调度问题提供了新思路。