一类社交网络中受媒介影响的信息传播动力学模型分析与最优控制

任亚鑫， 薛亚奎

(中北大学 数学学院， 山西 太原030051)

0 引 言

随着互联网行业的发展， 微信、 微博等在线社交媒体已经成为重要的信息来源， 为人们的生活提供了极大的便利。 目前， 大众媒体作为获取信息的媒介广泛传播着与疾病有关的信息， 人类响应和传递信息的行为在控制疾病传播方面发挥了重要的作用。

对疾病的意识意味着向人们分享有关该疾病的基本信息， 许多研究致力于人类意识对传染病传播的影响。 Wang等[1]提出了一个意识扩散和SIR传染病传播耦合的两层模型， 通过引入局部意识比率来分析意识扩散对传染病传播过程的影响。 Peng等[2]简单地考虑单一网络， 描述了意识和传染病传播之间竞争的过程。 上述研究都表明人们意识到采取保护措施会更有助于控制疫情蔓延， 可见意识传播是控制疫情不可忽视的因素， 但所建意识传播模型都较为简单。 因此， 近年来有学者对此开展了相关研究。 根据实际情形， 在模型中纳入讨论者[3]、 冷静者[4]、 超级传播者[5]等， 并在分析信息传播的过程中考虑了更多其他因素， 如记忆和遗忘机制[6]、 驳倒机制[7]、 信任机制[8]等， 可以对信息传播有一个更全面的认知。

Zhang等[9]考虑到社交网络信息传播过程中用户地位的不平等性， 讨论了具有高影响感染节点和普通影响感染节点的模型。 Yin等[10]研究了具有积极、 中立和消极情绪的信息传播模型。 然而， 上述模型都假设传播者直接成为免疫者。 但实际上， 当传播者与认为信息是虚假信息的熟人接触时， 传播者可能会逐渐减少信息的传播,而非直接成为免疫者。 文献[4]将这个变化期称为“冷淡期”， 并把这一情形考虑到ILSCR (Ignorants Latents Spreaders Cooled Removed) 模型中进行研究.为方便起见， 本文将处于“冷淡期”类别的个体称为冷静者。 信息传播的方式多种多样， 但以上研究都局限于一种传播方式， Jia等[11]虽然考虑了信息传播渠道(点对点传播和群体传播)之间的差异， 但建立的仅是SIR模型， 并且没有进行优化控制分析。

鉴于此， 本文综合考虑了点对点与群体传播方式间的差异以及传播者对信息传播具有冷淡期等情形， 提出了受媒介影响的ISCR动力学模型， 并进行了稳定性和优化控制分析。

1 模型的建立

将总人群N(t)分为4类： 无知者I、 传播者S、 冷静者C、 免疫者R。 信息传播过程如图1 所示。

对图1 中的两种传播方式做如下解释：

图1 ISCR信息传播过程

1) 在群体传播方式下， 无知者以速率β1变为传播者， 以速率ω变为免疫者； 在点对点传播方式下， 以速率β2变为传播者， 以速率ω变为免疫者。

2) 传播者以概率γ1选择群体方式进行信息传播， 以概率γ2选择点对点方式进行信息传播。

3) 当传播者与认为信息是虚假信息的熟人接触时， 传播者开始逐渐对信息传播变得冷淡， 以速率φ成为暂时停止传播的冷静者， 然后以速率α成为免疫者。

在文献[11]的基础上， 增加冷静者类别， 建立信息传播模型

式中：β1为群体传播感染率；β2为点对点传播感染率；γ1为群体传播选择率；γ2为点对点传播选择率；ω为失去传播兴趣率；Λ为迁入率；μ为迁出率；φ为冷淡率；α为恢复率；δ为复发率； 〈k〉为网络的平均度。 各参数及变量均非负。 为描述方便， 令m1=β1γ1+β2γ2/〈k〉，m2=ω(γ1+γ2/〈k〉)。

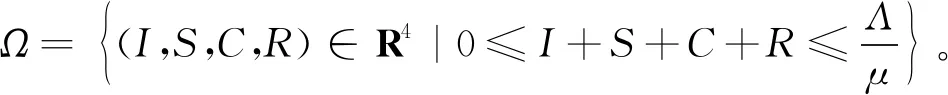
(1)

2 基本再生数与平衡点的存在性

(2)

模型(Ⅰ)的基本再生数等于ρ(FV-1)， 即

定理 1当R0>1时， 模型(Ⅰ)存在唯一的正平衡点E1=(I*，S*，C*，R*)。

证明令模型(Ⅰ)右端等于0， 求解得到

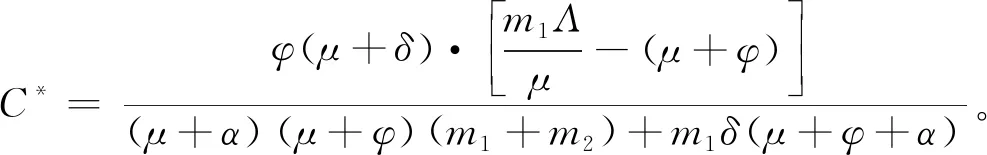
(3)

3 稳定性分析

3.1 无信息平衡点的稳定性

根据文献[12]中的定理2可知， 必有引理1成立。

引理 1当R0<1时， 模型(Ⅰ)的无信息平衡点E0在Ω内局部渐近稳定。 当R0>1时，E0不稳定。

定理 2当R0<1时， 模型(Ⅰ)的无信息平衡点E0在Ω内全局渐近稳定。

证明常见的Lyapunov函数方法证明E0的全局稳定性较为复杂， 本文借鉴文献[13]中的方法进行证明。

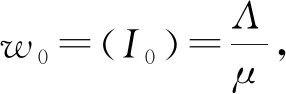
δR-μI。

(4)

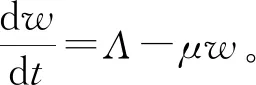
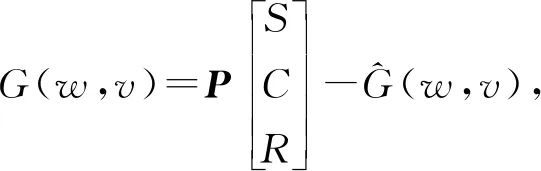
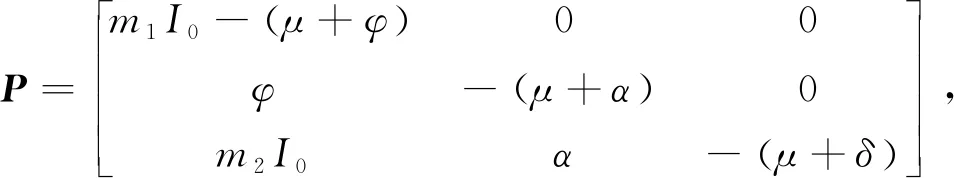
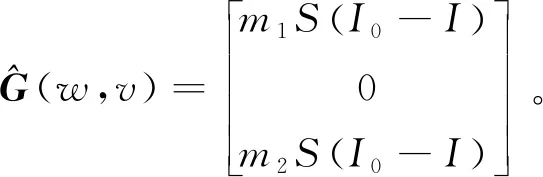
(5)

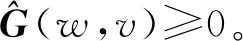
3.2 信息正平衡点的稳定性

定理 3当R0>1， 模型(Ⅰ)的信息正平衡点E1在Ω内局部渐近稳定。

证明模型(Ⅰ)在E1处的雅可比矩阵J(E1)为

(6)

矩阵J(E1)的特征值为式(7)的根

λ4+a1λ3+a2λ2+a3λ+a4=0，

(7)

其中，

a1=3μ+δ+α+(m1+m2)S*>0，

a2=(μ+α)[2μ+δ+(m1+m2)S*]+μ2+m1δS*+(m1+m2)m1S*I*+

[(m1+m2)S*+δ]μ>0，

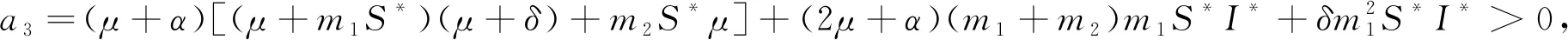
a4=μ(μ+α+φ)[μ(m1+m2)+δm1]S*+μαφ(m1+m2)S*>0。

(8)

为证明平衡点的全局稳定性， 将模型(Ⅰ)简化为如下极限系统[14-15]

模型(Ⅱ)的正不变集为

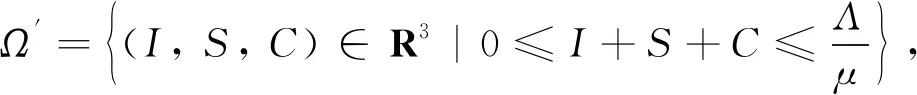
证明根据引理1及文献[16]中的命题3.3得， 当R0>1时， 模型(Ⅱ) 是一致持续的。

模型(Ⅱ)的第二加性复合矩阵[11，17]为

(9)

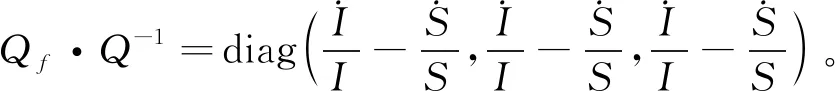
(10)

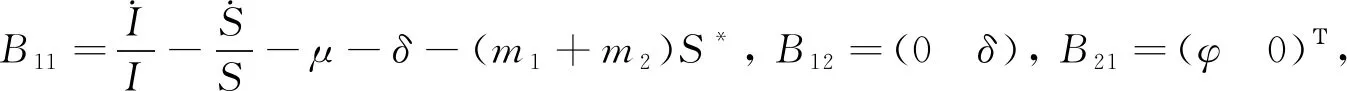
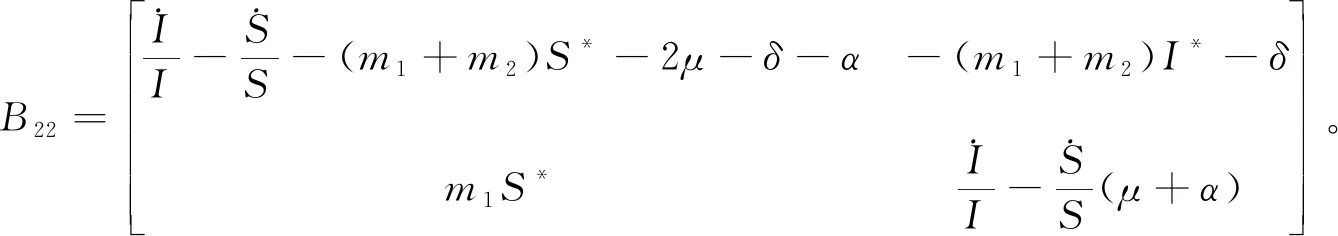
(11)

γ(B)≤sup{q1，q2}≡

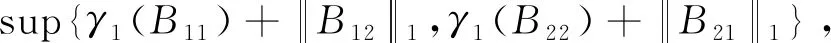
(12)

其中，

min{m2S*+μ，(m1+m2)I*}，

(13)

从式(13)中可得

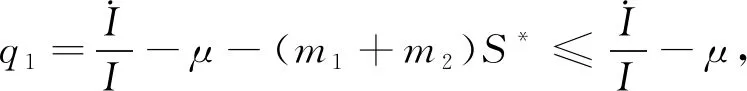
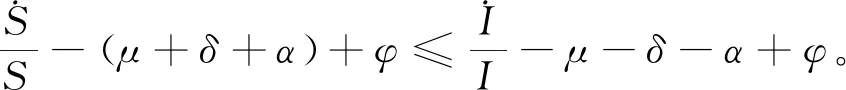
(14)

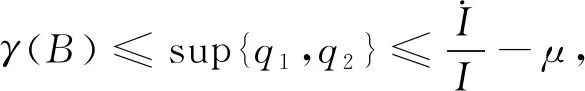
(15)

4 最优控制

在信息爆炸的时代， 减少虚假信息的传播以及提高公民辨别信息真伪的能力是社交网络中的关键问题[18]。 于是提出以下控制策略， 其中u1(t)代表政府进行干预管理， 如控制通信平台；u2(t)代表提高公民思考能力。 为分析控制虚假信息传播的最佳控制策略， 将模型(Ⅰ)改写为如下非线性微分方程组

设二次型形式的控制目标函数为

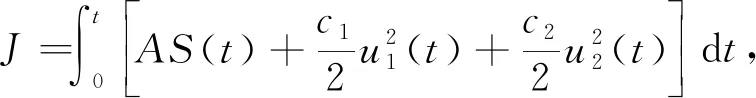
(16)

式中：t为末态时刻； 常数A，c1，c2为相应的权重系数。 寻找最优控制， 使得

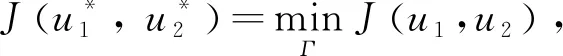
(17)

构建哈密顿函数H为

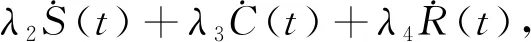
(18)

式中：λi(t) (i=1，2，3，4)为状态的连接变量。

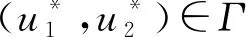
(19)

最优控制解的表达式为

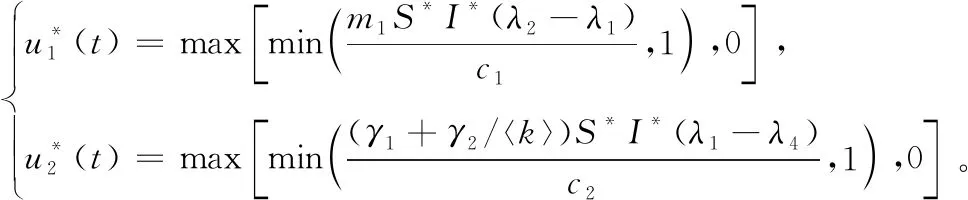
证明由Pontryagin’s最大值原理得

(21)

同时满足横截条件

λ1(T)=λ2(T)=λ3(T)=λ4(T)=0。

(22)

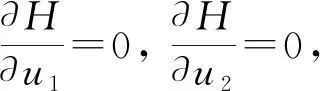
(23)

解出的最优控制解为

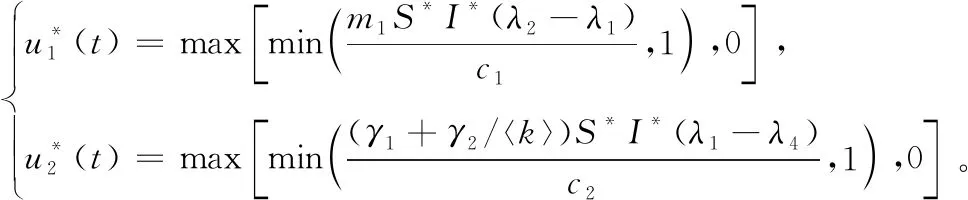
(24)

5 数值模拟

对上述理论进行数值模拟， 验证其正确性。 选取相同的初值为I(0)=0.85，S(0)=0.015，C(0)=0.1，R(0)=0.035。

图2 是无信息平衡点E0的全局渐近稳定性的模拟图。 参数选取为Λ=0.1，β1=0.25，γ1=0.5，β2=0.5，γ2=0.3，ω=0.1，φ=0.3，α=0.25，δ=0.1，μ=0.1， 〈k〉=5， 此时R0<1，S的图像曲线最终归于0， 表明信息最终消失.图3 是信息正平衡点E1的全局渐近稳定性的模拟图.参数选取为Λ=0.1，β1=0.6，γ1=0.7，β2=0.8，γ2=0.6，ω=0.1，φ=0.15，α=0.2，δ=0.1，μ=0.1， 〈k〉=5， 此时R0>1，S的图像曲线趋于一条直线， 表明信息会持续传播。

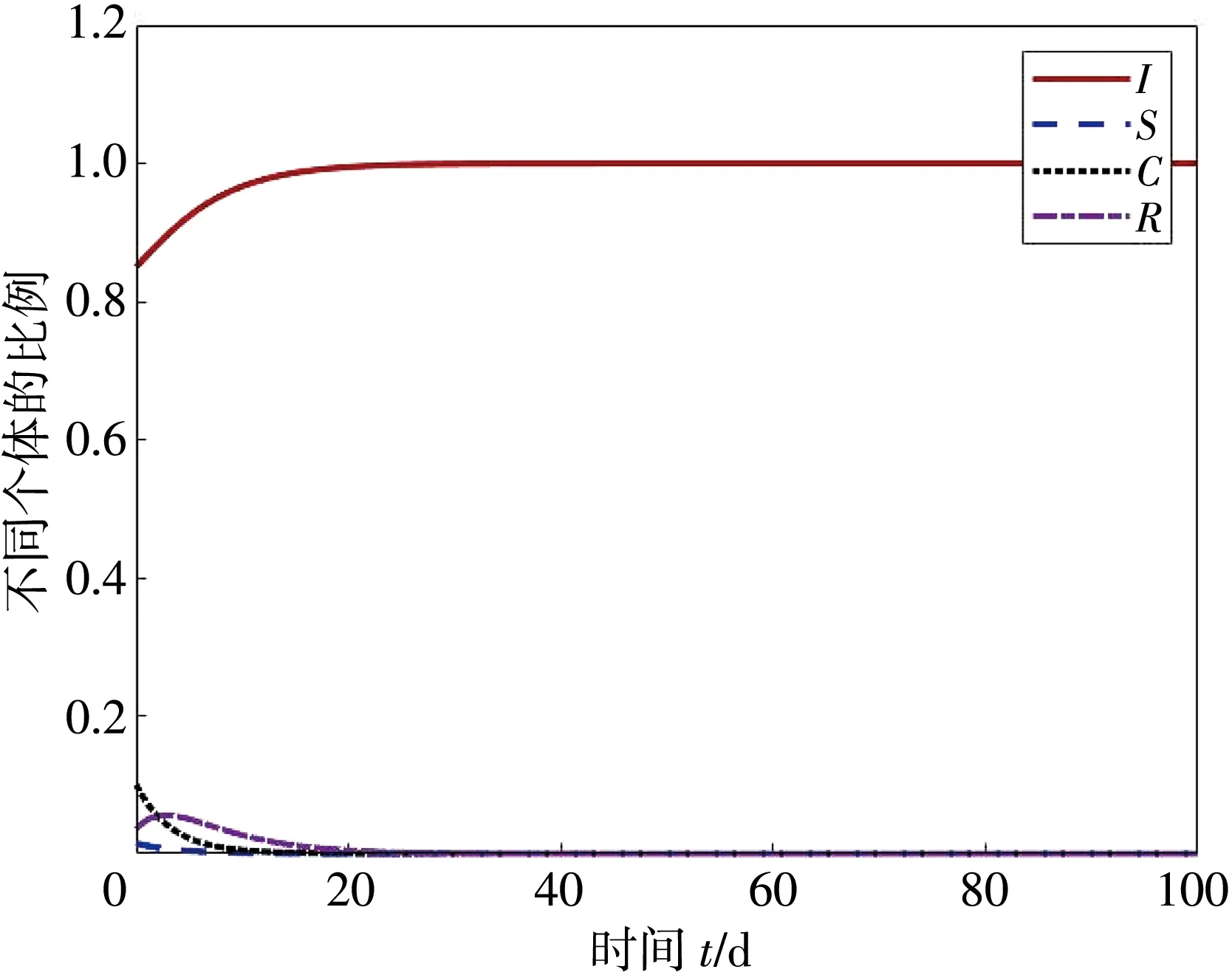
图2 E0的稳定性

图3 E1的稳定性

图4 模拟了冷淡率φ对传播者在总人群中所占比例的影响。 参数选取除φ不固定外， 其余与图3 参数选取相同。 图4 中传播者所占比例随冷淡率的增大而降低， 且受冷淡率φ的影响显著， 反映出在信息传播建模中考虑经历冷淡期这一阶段至关重要。 在现实中， 当传播有关疾病的基本信息时， 应减小φ以扩大传播者范围， 使更多的人意识到传染病的感染风险， 从而采取保护措施减少感染的可能性。

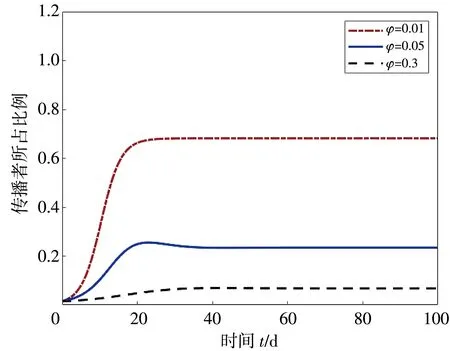
图4 冷淡率对传播者所占比例的影响

图5 模拟了不同传播方式的选择率γ1，γ2对基本再生数R0的影响。 参数选取为Λ=0.1，β1=0.8，β2=0.7，φ=0.3，μ=0.1， 〈k〉=5。 从图5 中可明显看出γ1对R0的影响远大于γ2对R0的影响， 即群体传播造成的影响要大于点对点传播方式。

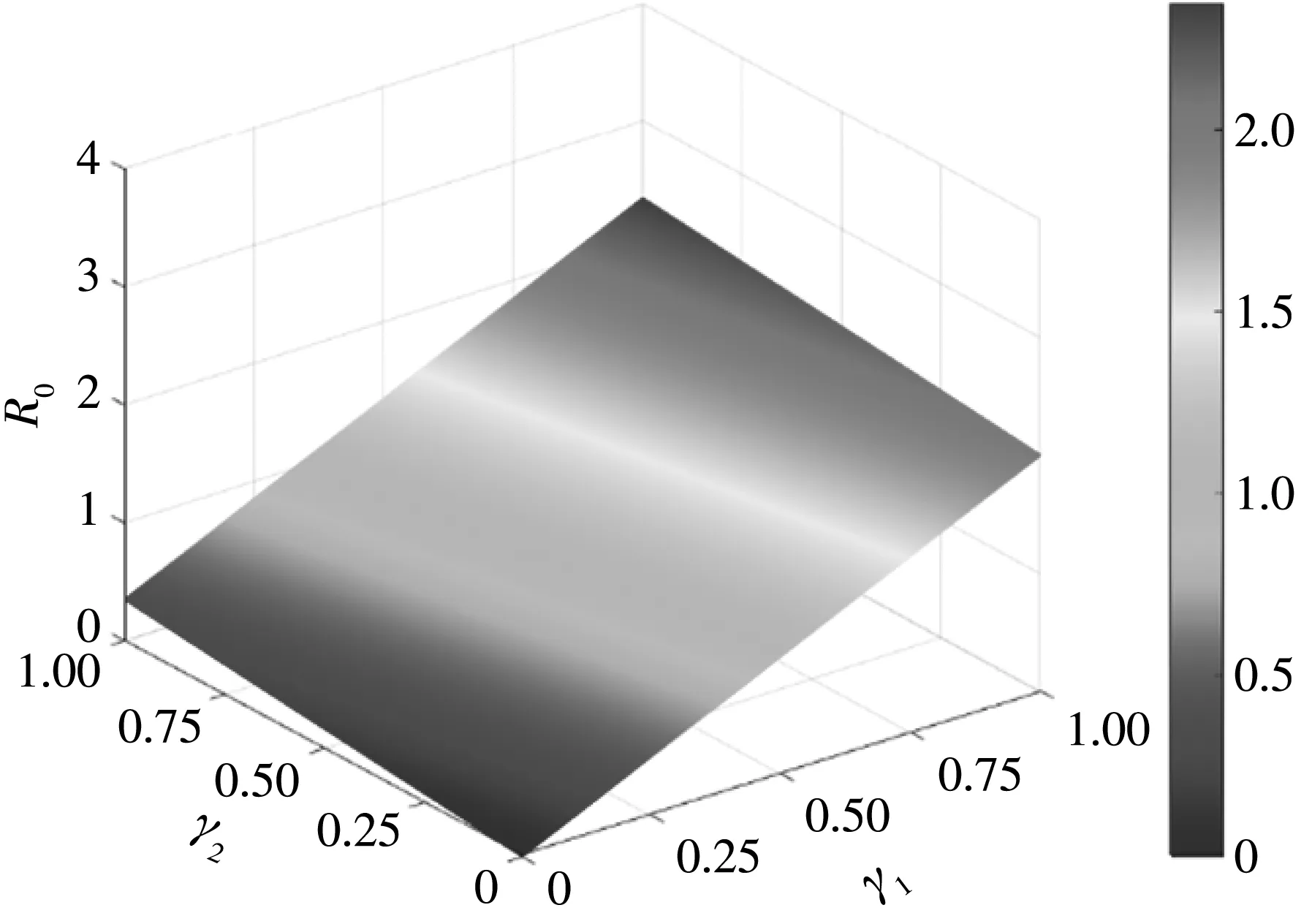
图5 不同传播方式选择率γ1， γ2对R0的影响

图6 为采取控制策略前后传播者数量的对比。 设置控制变量的边界u1=[0，0.7]，u2=[0，0.6]， 选取参数为Λ=0.5，β1=0.7，γ1=0.55，β2=0.4，γ2=0.3，φ=0.8，α=0.6，δ=0.08，ω=0.1，μ=0.6， 〈k〉=15。 权重参数设置为A=2，c1=1，c2=1。 图6 表明， 在传播虚假信息时， 该控制策略可有效减少传播者数量， 减轻虚假信息带来的负面影响。

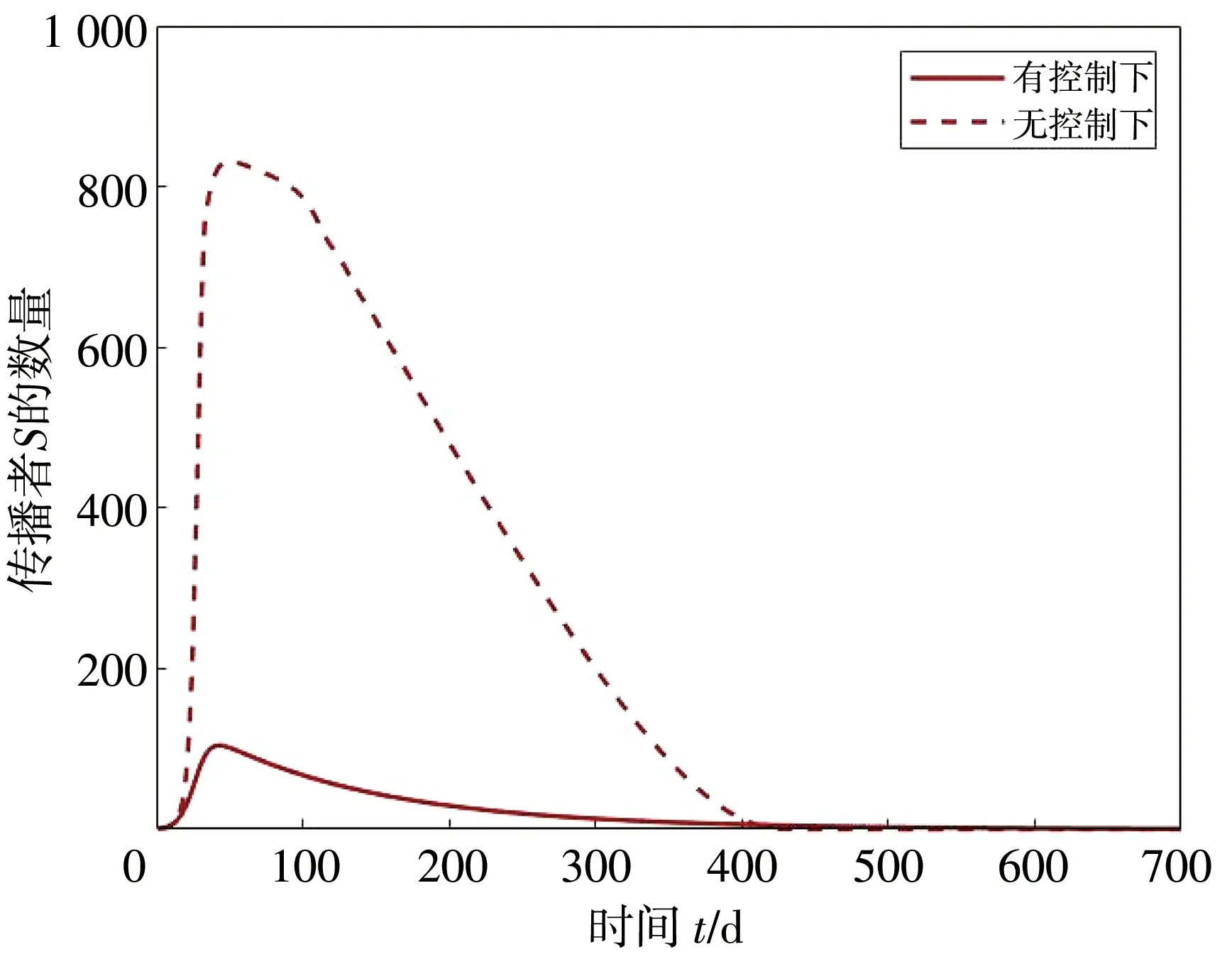
图6 传播者S的控制效果图

6 结 论

本文考虑到传播者在信息传播过程中经历冷淡期及点对点与群体传播方式的差异， 建立了ISCR动力学模型， 推导出了基本再生数R0及平衡点。 利用Hurwitz判据及几何方法证明了以下结论： 当R1<1时, 无信息平衡点E0全局渐近稳定； 当R0>1且φ<δ+α时, 信息正平衡点E1全局渐近稳定。 数值模拟结果与理论分析相吻合， 研究结果表明： 传播关于防范传染病的信息时，应减小冷淡率，并着重控制以群体方式进行的信息传播； 政府干预管理和提升公民思辨能力等策略是抑制虚假信息传播的有效措施。