移动边缘计算网络下基于静态贝叶斯博弈的入侵响应策略研究

范伟，彭诚，朱大立，王雨晴

（1.中国科学院信息工程研究所，北京 100093；2.中国科学院大学网络空间安全学院，北京 100049）

0 引言

近年来，5G 移动网络技术日渐成熟，网络设备智能化程度不断加深，网络中用户设备的数量和设备产生的数据量呈几何式增长，以云计算[1]为核心的集中式服务模式逐渐难以满足终端智能化和海量数据实时处理的需求，移动边缘计算（MEC,mobile edge computing）[2]应运而生。其具有如图1所示的基于“云-边-端”的三层分布式体系架构[3]。其中，“端”指终端层，既是数据的消费者又是数据的生产者，包括传感器、个人计算机、车辆等各类移动和固定的终端设备，负责与用户直接交互或收集各类原始数据并报告给边缘计算层。“边”指边缘计算层，位于靠近数据源头的网络边缘，由众多边缘节点构成，负责接收、存储和计算终端层上传的数据并有选择地交付给云计算层。“云”指云计算层，位于网络的中心，是距离终端层最远的一层，能够为整个网络提供更强的计算分析能力、更多的计算资源和全局分析服务。

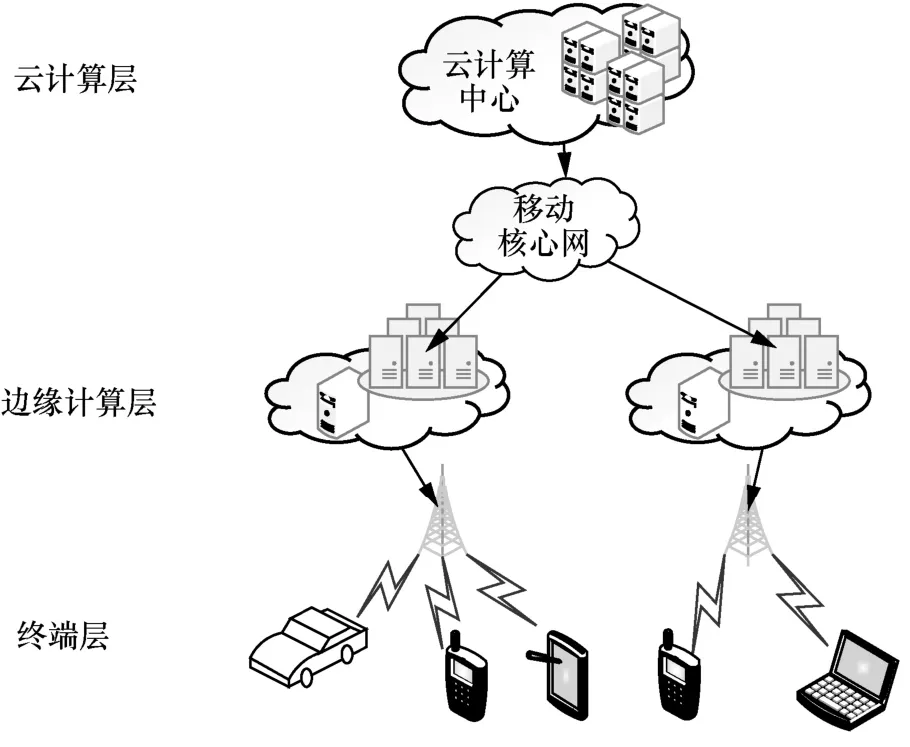
图1 MEC 基于“云-边-端”的三层分布式体系架构

MEC 通过将计算与存储资源迁移到网络边缘，使计算任务可以在靠近数据源头的边缘节点运行，有效地减小了数据的传输时延和带宽，缓解了云计算中心的压力，使实时性和时延敏感型应用得以更好地实现，但也带来了新的安全挑战。以拒绝服务（DoS,denial of service）攻击为例，云计算中心的DoS 攻击较集中，且一般的DoS 攻击难以攻破。而在移动边缘计算架构下，攻击主要是针对分布式的边缘节点进行的，由于其计算和存储资源相对较少，当攻击强度增大时，节点被攻陷的可能性极大。因此，与云计算中的攻击相比，针对移动边缘计算的攻击可通过提高攻击强度来获得成功。

移动边缘计算所面临的安全问题与云计算大同小异，主要是结构上的差异。一方面，边缘节点通常部署在距离终端用户较近的网络边缘，地理分布广泛且网络环境复杂，容易遭到恶意攻击者的攻击威胁；另一方面，在移动边缘计算环境下，由于设备结构、协议、服务提供商的不同，导致发生在边缘节点上的攻击过程难以被准确地检测[4]。此外，传统的入侵检测系统通常很少考虑系统资源状态的影响，可能出现系统响应攻击的损失大于真实攻击引起的损失的情况，无法适用于计算和存储资源有限的边缘节点。因此，需要引入一种新的入侵响应决策模型，使边缘节点能够有效地应对入侵者的入侵行为。

由于MEC 模式兴起的时间不长，目前，MEC入侵检测的研究不多，可分为基于边缘智能和其他方法两大类。基于边缘智能的方法主要包括基于机器学习[5]和基于深度学习[6]2 种，其他方法则包括基于博弈论、基于生物免疫原理等方法。

在基于机器学习的入侵检测方法研究中，主要采用随机森林、XGBoost、高斯朴素贝叶斯、k 近邻（KNN,k-nearest neighbor）等算法。Lee 等[7]考虑边缘节点计算资源受限的缺点，提出在边缘节点部署一种基于稀疏自编码器和支持向量机的轻量级入侵检测系统（IDS,intrusion detection system），实验结果表明，该IDS 可以获得98.22%的准确度。李忠成等[8]根据边缘计算网络开放、异构和资源受限的特点，设计通用的边缘计算IDS，并提出一种基于改进的训练样本筛选-极限学习机（TSS-ELM）的边缘计算入侵检测算法。相较于其他算法，该算法具有更优的准确性、时间依赖性、稳健性和误报率。基于机器学习的入侵检测方法具有训练和检测时间短、所需内存等资源较少的优点，但可构造的特征有限、检测率和准确率较低、缺乏可拓展性和稳健性。

在基于深度学习的入侵检测方法研究中，主要采用卷积神经网络（CNN）、循环神经网络（RNN）、长短期记忆网络（LSTM）等算法。由于深度学习算法的网络结构复杂、参数众多、训练需要海量的数据以及大量的计算和内存资源，需要设计轻量级的深度学习算法或将传统的深度学习算法进行轻量化才能应用于边缘计算环境。Sudqi 等[9]提出一种基于多层感知机模型向量空间表示形式的轻量级IDS，以解决边缘设备资源受限且容易遭受安全攻击的问题，该方法相比于同类入侵检测算法有更高的检测率和更低的计算复杂度。Souza 等[10]提出了一种可以在网络边缘运行的入侵检测架构，它采用基于深度神经网络（DNN,deep neural network）和KNN 的混合二元分类方法将事件分类为攻击和非攻击2 种，可应用多种机器学习方法对分类为攻击的事件进行检测，实验结果表明，该方法能够在经典机器学习方法中实现较高的精确度，并在内存和处理成本方面具有较低的开销。基于深度学习的入侵检测方法可以获得较高的检测率，但训练过程复杂、训练速度较低且需要强大的计算资源。

在基于博弈论的入侵检测方法研究中，研究目的不是求得对某种具体入侵行为的防御措施，而是寻求一种针对多种入侵行为的通用防御机制[11]，以有效地对非法入侵者及入侵检测系统之间的攻击与检测过程进行预测和分析[12]。An 等[13]将边缘网络中的攻击防御视作动态博弈过程，运用基于微分博弈论的入侵检测方法对边缘网络的入侵过程进行模拟，研究边缘节点的最优入侵策略及对应的最优响应策略。苗莉[14]利用平均场博弈和随机微分博弈等数学理论，在考虑边缘节点资源有限特征和恶意节点的攻击强度的基础上，对边缘计算环境下边缘用户数据、边缘节点和边缘网络的安全防御等问题进行了研究。基于博弈论的入侵检测方法采用不同的视角看待安全，即安全不是没有威胁，而是攻击系统比不攻击系统更加昂贵。相较于单纯对防御资源配置优化，它具有明显的优势：一是明确了模型中攻防双方行为的影响，而简单的优化公式只关注防御资源的优化，不考虑攻击者；二是博弈论具有内在的多玩家属性，不仅为防御算法的开发提供了基础，而且可以用来预测攻击者的行为[15]。

本文基于博弈论的入侵检测方法提出一种基于静态贝叶斯博弈的MEC 入侵响应决策模型。该模型可以对边缘节点的网络行为进行分析和预测，使MEC 系统在最小化节点资源消耗的前提下最大化抑制入侵者的入侵行为。本文的主要研究内容如下。

1) 将网络攻防过程映射到博弈过程中，建立基于静态贝叶斯博弈的MEC 入侵响应决策模型，并通过求解模型的贝叶斯纳什均衡，确定攻防双方的最优响应策略。

2) 针对MEC 实时性和可靠性要求高及边缘节点的能量与计算、存储、网络等资源受限的特点，考虑多种因素对攻防双方策略选取的影响，包括防御节点的资源、损失代价、防御成本，恶意节点的攻击类型、攻击成本以及防御系统的检测率和漏报率等，针对不同的安全目标采取不同的防御措施，使MEC 系统在面临外部攻击时可以实现入侵损害与防御成本之间的平衡。

3) 设计模型算法并进行数值分析。实验结果证明了模型的有效性，可以对攻击者和防御者的策略选择进行理性的预测，并抑制恶意节点的攻击行为。

1 模型设计与形式化描述

本文基于图1 提出一种与传统模式不同的入侵响应决策模型，如图2 所示。在所有的边缘节点中部署入侵检测代理，主要负责收集监测数据，而入侵检测这项耗费大量计算和能量资源的工作则由云计算中心完成。需要注意的是，不是所有监测到的行为数据都要提交到云计算中心，只有被入侵响应决策模型确定为采取检测策略的边缘节点上的入侵检测代理才会被触发并上传数据。

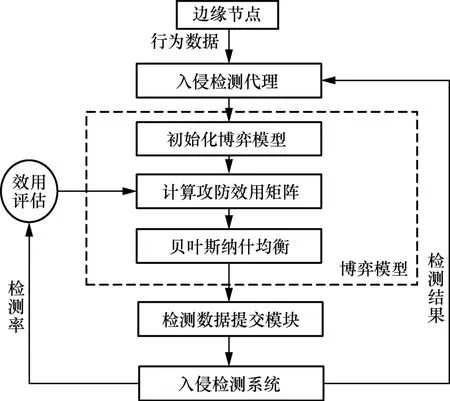
图2 入侵响应决策模型

边缘节点上的入侵检测代理在收集到监测数据后，面临是否将监测数据提交至云计算中心并启动入侵检测系统的问题。一方面，入侵检测代理只有提交监测数据才可能检测到恶意攻击者的攻击威胁；另一方面，入侵检测代理在提交监测数据时将消耗用于数据发送的能量和带宽，同时泄露包含在监测数据中的隐私数据（如边缘节点的位置信息等）。因此，需要建立MEC 入侵检测系统的最优响应决策模型，以在考虑MEC 系统入侵检测代理监测数据发送能耗和带宽等资源及边缘计算节点隐私保护因素的基础上，最优化入侵检测系统的响应决策。

1.1 模型设计

边缘节点包括恶意节点与防御节点。恶意节点的目的是破坏MEC 网络的安全，使边缘节点彻底瘫痪，而防御节点可以利用入侵检测系统对接收的信息进行检测。恶意节点为了掩饰自己的攻击行为也会给防御节点发送正常信息。防御节点对收到的信息进行检测需要消耗一定的能量，由于边缘节点的资源和能量有限，如果防御节点对收到的所有信息都进行检测，则很快会因能量耗尽而无法工作。因此，防御节点在决定是否进行检测时需要综合考虑其付出的能耗代价及被攻击的可能性，即恶意节点和防御节点的攻防行为其实就是一个博弈过程，攻防双方会在分析博弈局势的基础上采取对自己最有利的策略。因此，本节用博弈论的方法对攻防双方的策略进行分析。

定义1MEC 入侵响应决策模型。在考虑MEC入侵检测代理监测数据发送能耗和边缘节点隐私保护的基础上，将MEC 入侵响应决策模型表示为一个五元组[16]G=（N,θ,P,S,U），其含义如下。

1)N={i,j}是博弈参与人的集合。其中，参与人i代表可能会对其他节点或设备发动攻击的边缘节点或终端设备，参与人j代表部署了入侵检测代理的边缘节点。

2)θ={θi,θj}是博弈参与人的类型空间。在博弈过程中，恶意节点i和防御节点j无法确定对方的策略收益，但可以将策略收益的不确定性转换为类型的不确定性，并通过概率分布对对方的类型进行判断。MEC 网络中可能既存在正常类型的边缘节点也存在恶意类型的边缘节点，因此假设是边缘节点i的类型空间，分为正常类型和恶意类型。恶意类型的边缘节点i可能选择不攻击策略以混淆防御节点j的判断，而其最终目的是选择攻击策略以破坏MEC网络的安全，使边缘节点彻底瘫痪；而正常类型的边缘节点i不会发动攻击，可用于感知信息、转发数据等。是部署了入侵检测代理的边缘节点j的类型空间，可以选择检测策略将监测数据提交到云计算中心进行入侵检测，也可能因为考虑资源消耗和隐私保护的需要选择不检测策略。由于恶意节点的伪装以及无线信道噪声的影响，入侵检测系统在检测前无法确定节点i的类型是正常还是恶意，而防御节点j是已知的。按博弈论的说法，其身份信息对入侵检测系统的防御节点j而言属于私有信息，而防御节点j的类型对参与人双方而言是公共信息。

5) 效用函数U={ui,uj}是参与人在博弈时可以获得的收益，由参与人类型和其选择的策略决定。其中，ui表示节点i在策略集Si对应策略下进行博弈可得的收益，uj表示节点j在策略集Sj对应策略下进行博弈可得的收益。

在MEC 网络中，节点i与节点j的效用函数与多方面的因素有关，如防御节点j的资源、损失代价、防御成本，恶意节点i的攻击收益、攻击成本以及入侵检测系统的检测率和误测率等。表1 列出了参数及其含义，所有参数均为正值[17-19]。其中，防御节点j守护的资源的总价值为ω，它包括节点的能量、网络带宽、存储和计算资源以及安全相关的因素。在假设不存在节点因自私而争用网络资源的情况下，MEC 入侵响应决策模型可以看作零和博弈，即恶意节点i发动攻击成功后，防御节点j的损失与恶意节点i的收益相同，均为ω。此外，由于现有的入侵检测技术无法完全准确地区分系统的正常行为和攻击行为，导致不可避免地存在漏报和误报现象，因此将存在漏报和误报的概率定义为误测率β。当节点i进行攻击时，入侵检测系统会以α的概率发出正确警报；当节点j没有受到攻击时，入侵检测系统会以β的概率发出错误警报。

表1 参数及其含义

边缘节点i和部署了入侵检测代理的边缘节点j在进行博弈时共有6 组策略。对于策略组合，恶意节点i对部署了入侵检测代理的边缘节点j发动攻击，边缘节点j将收集到的监测数据提交至云计算中心并由云计算中心进行入侵检测。此时，防御节点j的收益等于检测到攻击时防御节点j的收益αbd减去防御攻击的成本cd，还需减去未检测到攻击时防御节点的损失（1 -α）ω，因此防御节点j的收益为αbd-cd-（1 -α）ω；恶意节点i的收益等于攻击未被检测到时恶意节点的收益（1 -α）ω减去攻击的成本ca，再减去攻击被检测到时恶意节点受到的惩罚αba，因此恶意节点i的收益为（1 -α）ω-ca-αba。对于策略组合，恶意节点i对部署了入侵检测代理的边缘节点j发动攻击，边缘节点j不提交监测数据启动入侵检测。此时，防御节点j的收益等于攻击成功时防御节点j的损失，即-ω；恶意节点i的收益等于入侵成功的收益ω减去发动攻击的成本ca，即ω-ca。对于策略组合和，虽然边缘节点i是恶意节点，但均采取不攻击的策略，所以2 种策略组合下恶意节点i的收益均为0。当防御节点j选择将监测数据提交并启动入侵检测时，节点j的收益包括防御的成本和因误测而导致的损失，即 -βbd-cd；当防御节点j不将监测数据提交时，节点j的收益等于边缘节点进行正常网络活动的收益bn。对于策略组合和，正常节点i只有不攻击一个可选策略，因此节点i的攻击收益总为0。当防御节点j选择将监测数据提交并启动入侵检测时，其收益为-βbd-cd；当防御节点j不将监测数据提交时，其收益为bn。

边缘节点i和部署了MEC 入侵检测代理的防御节点j进行博弈的攻防效用矩阵如表2 所示。效用表示部分（*,*）中，逗号左边代表节点i在相应攻防策略下的收益，逗号右边代表防御节点j在相应攻防策略下的收益。

表2 攻防效用矩阵

博弈过程中，防御节点j知道自己所属的类型θj，但不知道节点i的类型θi。为了表现这种不确定性，使用Harsanyi 转换引入一个虚拟的参与人——自然（N,Nature），由N 首先采取行动，决定边缘节点i的类型[20-21]。节点i和节点j对N 的行动拥有一个共同信念：N 以概率μ（0≤μ≤ 1）确定节点i的类型为恶意类型，以概率1-μ确定节点i的类型为正常类型，接着节点i和节点j开始行动，节点i首先选择是否采取攻击策略，然后防御节点j选择是否采取防御的策略。图3 所示的贝叶斯博弈树详细地描述了这个过程。

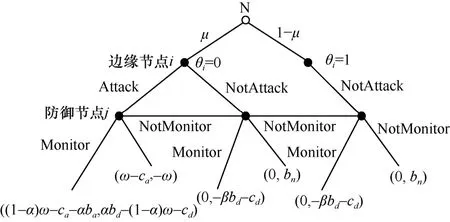
图3 贝叶斯博弈树

1.2 贝叶斯纳什均衡分析

1.1节给出的MEC 入侵响应决策模型属于静态贝叶斯博弈类型，对应的均衡概念称为贝叶斯纳什均衡，它是纳什均衡概念在静态贝叶斯博弈（又称不完全信息静态博弈）上的扩展，最大的特点是参与人可以在不确定其他参与人类型的情况下得出博弈的最优策略。

MEC 入侵响应决策模型中，恶意节点i与防御节点j的类型有限，且每种类型下攻防双方的行动组合也是有限的，即此博弈模型是一种有限的策略博弈。因此，根据纳什均衡的存在性定理[22]，在每个有限的策略博弈至少存在一个纯策略或混合策略纳什均衡。由于纯策略可以看作混合策略的特殊情况，则MEC 入侵响应决策模型必然存在一个混合策略的贝叶斯纳什均衡。由混合策略贝叶斯纳什均衡的定义可知，在纳什均衡状态下存在一组混合策略或策略组合，相比其他策略，攻防双方的收益最大。在不清楚对方策略的情况下，攻防双方都倾向于选择这一组策略或策略组合，以使己方的收益最大，即通过对混合策略贝叶斯纳什均衡进行求解一定能够得到最优入侵响应策略。下面对1.1 节给出的静态贝叶斯博弈模型的贝叶斯纳什均衡进行求解。

下面，求解MEC 入侵响应决策模型的混合策略贝叶斯纳什均衡。假设恶意类型的节点i以概率p选择攻击策略，以概率1-p选择不攻击策略，防御节点j以概率q选择检测策略，以概率1-q选择不检测策略，且满足0 ≤p,q≤1 。防御节点j选择检测策略的期望效用为

2 算法步骤

在运用1.2 节得到的结果时，首先依据1.1 节设置移动边缘计算入侵响应决策模型的博弈参数，然后依据表2 初始化博弈模型的攻防效用矩阵，一旦部署在边缘节点上的入侵检测代理监测到其他节点发出的行为数据后，就依据表3 计算最优的响应策略，根据响应策略决定是否将监测数据发送到云计算中心并采取入侵检测，实现最大化抑制入侵节点的入侵行为。具体算法如算法1所示。

表3 入侵响应决策博弈的贝叶斯纳什均衡

算法1最优响应策略求解算法

输入静态贝叶斯博弈模型

输出防御节点的最优响应策略

1) 根据网络收集的数据，初始化博弈模型G=（N,P,S,U）；

2) 循环每对攻防策略，计算攻防效用矩阵；

3) 求解纳什均衡，计算贝叶斯纳什均衡；

5) 恶意节点以概率p*选择攻击策略，以概率1-p*选择非攻击策略；

7) 对入侵检测系统的检测结果进行判断，若判断结果是攻击，则防御节点以q*的概率启动防御机制，否则防御节点以1-q*的概率不启动防御机制；

8) 判断是否已检测网络中的全部节点，若是则结束博弈，否则返回步骤2)。

最优防御策略选取算法流程如图4 所示。

图4 最优防御策略选取算法流程

算法1 的复杂度取决于贝叶斯均衡的求解和攻防策略的规模。时间复杂度是由调用的攻防策略决定的，即调用纳什均衡的次数。由于纳什均衡算法的时间复杂度是多项式级别的[23]，即在策略规模为常数的模型中时间复杂度是多项式级别，满足移动边缘计算网络对实时性的要求。一次纳什均衡操作涉及确定攻击策略的概率以及选择攻击策略。设|A|为参与人边缘节点i空间的大小，|B|为参与人防御节点j空间的大小，则防御节点j要遍历边缘节点i空间|A|2次。全部节点需要进行n次检测才能得到最终的结果，因此整个算法的时间复杂度为O(n|A|2|B|)。

存储空间消耗主要集中在策略防御成本和均衡求解中间值的存储上，符合移动边缘计算节点资源受限的特点。防御节点选择防御策略的成本为cd，类型空间包含恶意节点和正常节点两类，所有节点空间要遍历|AB|2次，则每个贝叶斯纳什均衡的空间消耗为O(cd|AB|2)。全部节点需要进行n次检测才能得到最终的结果，因此整个算法的空间复杂度为O(ncd|AB|2)。

3 数值分析

采用数值分析的方法计算基于静态贝叶斯博弈模型的最优响应策略，分析入侵检测系统的检测率、误报率、检测次数、恶意节点的攻击成本与攻击收益的比值和防御节点的防御代价与不防御损失的比值对恶意节点选择攻击策略的概率和防御节点选择防御策略的概率的影响。考虑移动边缘计算的实际情况，攻防双方效用参数及取值如表4 所示。虽然这些参数设置了选定的值，但合理改变这些参数值也能得到类似的实验结果变化趋势。

表4 攻防双方效用参数及取值

图5 和图6 分别展示了入侵检测系统的检测率α对恶意节点和防御节点策略选择的影响。从图5 和图6 可以看出，随着α的增大，恶意节点i选择攻击策略的概率变小且与β的取值有关，防御节点j选择防御策略的概率也变小且与β的值无关。这是因为当入侵检测系统的检测率α增大时，恶意节点的攻击行为被系统检测出的概率会变大，而被检测出攻击行为的节点损失势必增大，因此恶意节点选择攻击策略的概率会降低，进而导致防御节点的检测率变低。如果防御节点继续保持当前的检测率和检测能耗不变，则防御节点的整体收益就会降低，因此防御节点也会降低检测率。

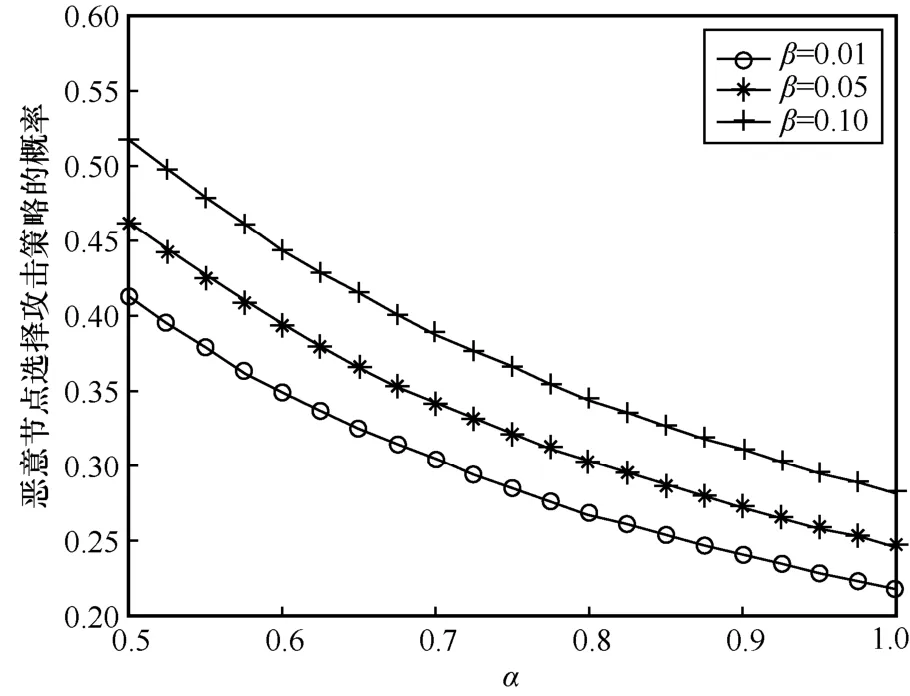
图5 α 对恶意节点选择攻击策略的影响

图6 α 对防御节点选择防御策略的影响

由图5 和图6 所示的概率变化可知，如果期望保持当前的概率不变，同时避免过高的检测次数导致整体的收益降低，也可以通过减少检测的次数，以达到高效检测的目的，进而节省边缘节点的能量。图7 展示了保持防御成功收益不变的情况下，检测次数对防御节点选择防御策略的影响。从图7 可以看出，防御节点j选择防御策略的概率随着bd值的增大而增大，防御成功收益对节点选择防御策略具有正向的刺激作用。同时，随着检测次数的增大，防御节点选择防御策略的概率不会持续增加，而是会在增加到某一个值之后趋于平稳。如果想在保持当前的防御成功收益的同时节省边缘节点的能量，那么检测次数就不能过高，否则防御节点也会降低选择防御策略的概率。

图7 检测次数对防御节点选择防御策略的影响

图8 和图9 分别展示了入侵检测系统的误测率β对恶意节点和防御节点策略选择的影响。不难看出，入侵检测系统误测率β越大，恶意节点i选择攻击策略的概率越大，而防御节点选择防御策略的概率不随β值的变化而变化。这是因为当入侵检测系统的误测率β增大时，防御节点被攻击的损失增大，因此防御节点会增大选择防御策略的概率。而防御节点选择防御策略的概率增加时，势必会使恶意节点的攻击成功率降低，如果恶意节点继续保持选择攻击策略的概率不变（攻击能耗不变），那么恶意节点的整体收益就会降低，因此恶意节点会降低选择攻击策略的概率。

图8 β 对恶意节点选择攻击策略的影响

图9 β 对防御节点选择防御策略的影响

由此可知，入侵检测系统的检测精度越高（即检测率α越大、误测率β越小），恶意节点采取攻击策略的可能性越低。因此，网络防御者可以通过提升入侵检测系统的检测精度来减少攻击事件的发生，从而节约防御攻击的成本。

边缘节点资源受限使恶意节点可以通过增大攻击强度入侵边缘节点。恶意节点的攻击强度与节点的攻击成本和攻击收益有关。同等条件下节点的攻击强度越大，发动攻击的成本越高，在防御节点未检测到攻击时的收益也越多，同时防御节点防御攻击的成本增加，未能有效防御攻击时的系统损耗增高。图10 和图11 分别展示了α=0.7、β=0.05条件下恶意节点的攻击成本与攻击成功收益的比值和防御节点的防御成本与防御失败代价的比值对恶意节点和防御节点策略选择的影响。如果攻击成功收益大于攻击成本或防御成功收益大于防御成本，依据博弈参与者“唯利是图”的特性，攻击者没有攻击的动机，防御者也没有防御的理由，因此。当时，随着的不断增大，攻击成本与攻击成功收益之间的差距越来越小，导致恶意节点发动攻击的概率越来越小，因此防御节点选择防御策略的概率越来越小，而恶意节点选择攻击策略的概率不随值的变化而变化。当时，随着的增大，防御成本越来越大，导致恶意节点选择攻击策略的概率变大，直至恶意节点选择攻击策略的概率达到1，随后不再增加，而防御节点选择防御策略的概率不变。这是因为在基于静态贝叶斯博弈的最优防御策略选择模型中，攻击者和防御者的选择依赖于对方而非自身的情况。因此，攻击者和防御者可以根据对方的情况，做出最理性的选择。

图10 对恶意节点和防御节点策略选择的影响

图11 对恶意节点和防御节点策略选择的影响

总结实验结果变化趋势可知，各种因素中对移动边缘计算入侵检测代理响应决策影响最大的是检测率α，其次是和检测次数，最后是误测率β和。这与入侵响应决策的实际情况一致，当入侵检测系统的检测精度增大时，恶意节点选择攻击策略的概率降低，从而节约防御攻击的成本。另外，模型不仅能对恶意节点选择攻击策略以及防御节点选择防御策略的概率进行预测，还能在入侵检测系统检测精度不高的情况下，直接根据检测结果进行决策，并减少不必要的资源消耗。这对实际系统研发具有指导意义。

将本文所提基于静态贝叶斯博弈模型的最优响应策略与常用的入侵检测算法进行比较，应用效果对比如表5 所示。从表5 可以看出，本文基于静态贝叶斯博弈的MEC 入侵响应决策模型能在入侵检测系统中获得较高的检测率及较低的误报率和漏报率，优于具有最快检测时间的朴素贝叶斯算法，整体表现优于随机森林算法，检测时间明显低于DNN 算法。同时，在时间成本、内存和处理成本方面相对具有更低的开销，在实时性上强于机器学习和深度学习算法，模型运算过程相对简单、节省有限的计算资源，更适用于计算和存储资源有限的边缘节点。

表5 入侵检测算法应用效果对比

基于本文的研究成果，可以制定以下措施来降低恶意节点发动攻击的概率，从根源上保障MEC网络的安全。1) 加大对发动攻击行为的恶意节点的惩罚，促使防御节点积极地应对恶意节点的攻击，提高检测率；2) 通过优化入侵检测算法来降低防御节点的检测能耗，从而降低恶意节点发动攻击的概率；3) 适当减小边缘节点的通信半径，这一方面可以降低通信范围内恶意节点的数量，另一方面也可以节约边缘节点的能耗，延长其使用寿命。

4 结束语

本文提出了一种适用于移动边缘计算环境的入侵响应决策模型。模型通过深入研究边缘节点和攻击者之间的交互行为，并结合边缘节点地理分布广泛、网络环境复杂、资源受限等特点，建立了基于静态贝叶斯博弈的入侵响应决策模型，模拟攻防双方在单次博弈中的行为选择，预测出博弈过程中攻击者选择攻击行为和防御者选择防御行为的概率。模型综合考虑系统的资源状态、入侵响应的成本以及入侵检测系统的检测率、误报率和漏报率等因素对防御策略选取的影响，使移动边缘计算系统在面临外部入侵时遭受的损失最低，且对整个网络的时延影响较小，满足移动边缘计算网络对实时性和可靠性的要求。仿真结果表明，该模型为防御者产生了更节能的防御策略，同时提高了系统的整体检测能力。