SPS 结构大规模S 盒设计与分析

张岚，何良生,2，郁滨

（1.信息工程大学密码工程学院，河南 郑州 450001；2.国家密码管理局，北京 100036）

0 引言

非线性编码是分组密码算法的主要模块，混淆性能较好的非线性编码设计是分组密码算法研究的重要内容。目前，常用的非线性编码为S 盒，它是分组密码算法的关键部件，主要提供算法所必需的混淆作用，其密码强度直接影响整个密码算法的安全强度。尤其是大规模S 盒，其极大地提高了非线性编码的线性度和差分均匀度，可以在较少的轮数内使分组密码达到抵抗差分分析和线性分析的安全界。

大规模S 盒一般是由小规模S 盒通过某种结合规则满足一定的约束条件构造的，可分为以下4 种情形。第一种情形是利用密码学结构如MISTY、Feistel 或直接由小规模S 盒并置构造大规模S 盒，基于3 轮平衡Feistel 结构[1-2]、3 轮Lai-Massey 结构[3]及3 轮MISTY 结构[4]构造大规模S 盒，可使S 盒密码性质适中并减少硬件资源占用。其中，MISTY[5]使用2 个9 bit 置换与一个7 bit 置换，使用3 轮MISTY 结构构造16 bit 大规模S 盒，再使用3 轮MISTY 结构构造32 bit 非线性置换，这种嵌套结构可提高整个非线性环节的密码学性质，但需合理选择内嵌的非线性函数。文献[6]提出一种新的8 bit 轻量化S 盒设计方法，其单轮逻辑运算仅涉及4个单比特逻辑与运算和4个单比特逻辑异或运算，迭代4轮后密码性质可达到差分均匀度为16、非线性度为96，分量函数的代数次数能达到6 且整体平衡。NUX[7]直接使用4 个4 bit 置换并置合成16 bit S 盒，这种构造方式适合轻量级密码设计，但不能提高S 盒的密码学性质。第二种情形是基于SPS 结构构造。Piccolo 算法[8]采用了SPS 结构构造的16 bit S 盒，其中，小规模S 盒为4 bit，线性层为4×4 的有限域上的极大距离可分（MDS,maximum distance separable）矩阵，但是MDS 矩阵硬件实现占用资源多。第三种情形是基于非线性反馈移位寄存器（NFSR,nonlinear feedback shift register）直接构造，如CACR2019 密码学会商用密码征集算法中NBC 算法[9]基于16 级非线性移位寄存器构造的16 bit S 盒，以及SPRING 算法[10]中4 个8 bit寄存器互相反馈的环状串联结构构造的32 bit S 盒，但是这2 种方式构造的大规模S 盒分别需要迭代20轮或32 轮，硬件实现时延较大，而且32 bit S 盒目前仍难以完全刻画其差分均匀度和非线性度等密码性质。美国国家标准与技术研究院（NIST）发起轻量级密码算法公开征集[11]，最终入围算法中SPARKLE[12]及GIFT-COFB（combined feedback）[13]等算法均采用了32 bit 或者64 bit 大规模密码S 盒。第四种情形是基于ARX 结构构造的大规模S 盒，2020 年美洲密码会上，Christof 等[14]基于ARX 结构构造了64 bit S 盒Alzette，仅使用循环移位、异或及模232加基于4 轮平衡Feistel 结构构造64 bit S 盒，在现代CPU 上仅需12 条指令迭代两次就可达到与AES 一样安全，不过由于64 bit S 盒规模较大，其密码学性质不易刻画。因此，大规模S 盒构造不仅要合理选择密码结构，而且对S 盒的尺寸也有要求，即至少能有效刻画其密码学性质。

基于SPS 结构大规模S 盒的构造主要体现在线性扩散层P置换的设计上，P置换安全性设计指标主要是分支数，分支数反映了扩散变换的好坏，分支数越大，扩散变换效果越好。分支数与差分分析、线性分析密切相关，利用P置换的分支数，评估活跃S 盒数目的下界，从而量化分组密码抵抗差分分析和线性分析的能力。近些年，分组密码扩散层的研究成果非常丰富，主要有以下三类。1) 利用MDS码构造最优扩散层。基于线性变换与线性码的联系，寻找较大分支数的线性变换，也就是寻找距离较大的线性码，极大距离可分码的分支数达到了最大值，其对应的MDS 矩阵是扩散层构造的较好选择，AES[15]、FOX[3]等分组密码都采用了MDS 扩散层。2) 利用MDBL（maximum distance binary linear）码构造最优扩散层。MDBL 矩阵的分支数是二元域矩阵所能取到的最大可能值，与MDS 矩阵相比，MDBL 矩阵的扩散速度略慢，但由于不涉及有限域上的乘法，其硬件实现通常更加轻量化，而且MDBL 矩阵更加灵活，更易于适应各种平台的优化实现，uBlock 分组密码[16]采用了MDBL 扩散层。3) 利用具有良好数学性质的循环矩阵构造最优扩散层[17-18]。基于循环矩阵的构造策略被分组密码广泛采用，在循环矩阵中，任意行向量的每个元素都是前一行向量的各个元素依次右移一个位置的结果，从而使硬件实现复用乘法电路以节省硬件面积，利用循环矩阵可以非常灵活地在硬件面积和实现时延间进行折中。

基于SPS 结构构造的大规模S 盒作为分组密码算法的非线性核心部件，不仅大幅提高了算法抵抗差分/线性密码分析的攻击能力，而且给算法整体结构采取何种性质的线性变换留下了很大的选择空间。Donut[19]使用4 个8 bit 置换基于SPS 结构构造32 bit大规模S盒，线性变换P是基于4×4有限域上的MDS 矩阵；Saturnin[20]使用4 个4 bit 置换基于SPS 结构构造16 bit 大规模S 盒，4 bit 置换为最佳置换，线性变换P为4×4 有限域上的MDS 矩阵。但是，由于有限域上MDS 矩阵乘法运算的存在，硬件实现面积较大，导致传统MDS 不适用于射频识别（RFID）系统和传感器网络等资源受限的环境。为了解决这一问题，Sajadieh 等[21]基于线性反馈移位寄存器（LFSR）提出了迭代型MDS 矩阵扩散层的构造方式，在保证最优分支数的前提下，极大地节省了硬件实现面积。Wu 等[22]将矩阵元素扩充到多项式环上，利用不同类型的LFSR 结构设计轻量级最优扩散层。Augot 等[23]通过分析迭代矩阵的穷举搜索结果，结合BCH 码相关结论，提出了最优迭代扩散层的直接构造算法。除硬件实现面积之外，时延也是扩散层设计的一个重要参数。Li等[24-25]研究了低时延迭代型MDS 矩阵和对合MDS矩阵的构造。Guo 等[26-27]通过提取矩阵可逆的充要条件以及分支数等价的划分原则，刻画了逆矩阵的具体形式和基本特征，提出了循环移位异或型最优扩散层的构造算法。文献[28]提出一种利用线性变换输入与输出关系反证得出分支数大小的普适方法，证明了一类由循环移位与异或运算构造的轻量级扩散变换是最优线性变换。

本文借鉴文献[28]线性变换输入输出关系反证法的思想，提出将最优线性变换目标问题转化为若干个递进关系定理的证明方法，不仅解决了该类最优线性变换的证明，而且适用于任意线性变换的证明，并在此基础上研究了2 轮SPS 结构的大规模S 盒构造问题。本文主要贡献如下：基于循环移位与异或运算构造了有限域上分支数最佳的线性变换P，给出了该类最优线性变换的一种新的证明方法，建立了2 轮SPS 结构的大规模S 盒模型，通过小规模S 盒与最优循环移位-异或型矩阵，设计了一系列密码学性质优良的轻量级大规模S 盒，与已有大规模S 盒构造方法相比，本文的大规模S 盒设计方案运算代价更加低廉，其差分、线性等密码学性质更加优良。

1 基本概念及引理

定义7[30]对于2 个n×n阶二元矩阵P和Q，如果存在一个行置换ρ和一个列置换γ，满足ρ(γ(P))=γ(ρ(Q))=Q，则称P和Q为置换同形矩阵。

引理1[30]若2 个n×n阶二元矩阵P和Q是置换同形的，则P和Q具有相同的分支数，即Bd(P)=Bd（Q）。

引理2[29]假设分组密码算法轮密钥是随机独立均匀分布的，且与每轮的输入数据按照逐比特异或运算。若线性扩散层的分支数为d，小部件S 盒的最大差分概率为p，则SPS 结构函数差分概率的上界为pd-1。

引理3[29]假设分组密码算法轮密钥是随机独立均匀分布的，且与每轮的输入数据按照逐比特异或运算。若线性扩散层的分支数为d，小部件S 盒的最大线性概率为q，则SPS 结构函数线性概率的上界为qd-1。

定义8一般形式。设X∈()m，定义基于循环移位与异或运算的线性变换为

其中，0 ≤li＜li+1＜nm，1≤r≤nm。

引理4[31]线性变换L(X,m,n)是最优线性变换必须满足以下2 个必要条件。

1)r为奇数且r≥m。

2) 至少存在m个li,满足ni≤li＜n(i+1)，i= 0,1,…,m- 1。

2 一类最优循环移位-异或型线性变换的证明

本节根据第1 节给出的一般形式和必要条件，讨论最简形式下的最优循环移位-异或型线性变换，即最优线性变换中循环移位项数最少的形式。本节给出了输入为 ()4扩散层中最简形式下的最优线性变换，并对其中一种进行了详细证明。

需证明所有ai,bi(i= 0,1,2,3)的非0 个数之和不小于5。下面分别讨论a0,a1,a2,a3中至少有一个不为0 情况下A和B的非0 个数之和，也就是A的非0 个数分别为1、2、3、4 时上述线性扩散变换的分支数。从式(6)～式(9)可以看到，b0,b1,b2,b3的形式相似，所以分类讨论时，从a0,a1,a2,a3中任意选取ai不为0 后会得到相似形式的b0,b1,b2,b3，所以不同ai的选取对证明过程不会产生影响。

3 SPS 结构大规模S 盒

2 轮SPS 结构大规模S 盒如图1 所示。其基本思想如下：mnbit 输入依次进入第一层混淆层、扩散层P和第二层混淆层，每个混淆层均由n个mbit小规模S 盒并置而成，该小规模S 盒均选择相同的mbit S 盒，扩散层P是mnbit 规模的线性置换。P可看作上基于循环移位-异或型分支数最佳的线性变换。因此，本节主要研究循环移位-异或型最优线性变换。

图1 2 轮SPS 结构大规模S 盒

3.1 16 bit 最优线性置换

令n=m=4，采用循环移位和异或运算组合操作构造线性置换P，使其差分和线性分支数达到最佳5。对于SPS 结构中使用的16 bit 线性置换P，可以统一表示为

根据定理6，当n=4、t=1 时，可得16 bit 最优线性变换P1(x)为

根据推论1，当n=4、t=3 时，可得16 bit 最优线性变换P2(x)为

由性质1 可知，对于线性置换P′，如果其循环移位数满足=(ti+4)mod16,i= 1,2,…,5，则线性置换P和P′的分支数相同.

由性质2 可知，对于线性置换P′，如果其循环移位数满足= (16 -ti)mod16,i= 1,2,…,5，则线性置换P和P′的分支数相同。

考虑到线性置换循环移位等价性质，与置换P1和P2等价的线性置换如表1 所示。

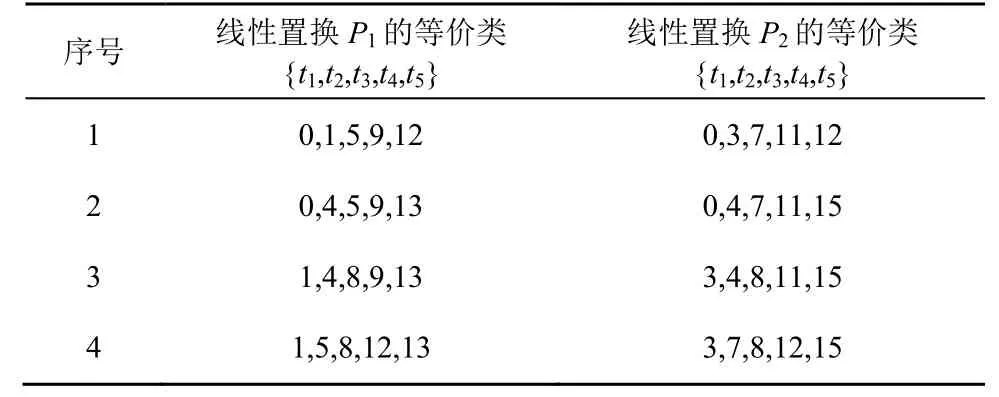
表1 线性置换P1 和P2 的等价类

基于此，小规模S 盒选用4 bit 置换，根据图1描述的大规模S 盒模型可以构造一系列具有相同优良密码学性质的16 bit S 盒。

3.2 32 bit/64 bit 最佳线性置换

32 bit/64 bit 最佳线性置换可由16 bit 最佳线性置换通过一定的规则变换得到，对于SPS 结构中使用的32 bit 线性置换P，可以统一表示为

定理7若两类16 bit 最佳线性置换如式(10)和式(11)所示，该16 bit 最佳线性置换对应的循环移位-异或型矩阵为是一个MDS 矩阵，将式(10)和式(11)的循环移位数和模数分别扩大2 倍，则32 bit 最佳线性置换的2 个等价类分别为

同理，考虑到线性置换循环移位等价性质，与置换P3和P4等价的线性置换如表2 所示。

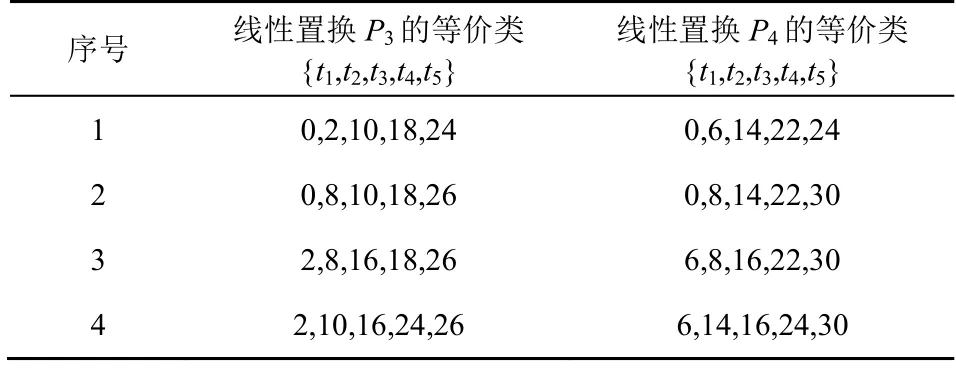
表2 线性置换P3 和P4 的等价类

根据线性置换循环移位数的等价性质，即=(ti+8)mod32,i=1,…,5，可知属于相同等价类的线性置换构造的32 bit S 盒具有相同的最大差分和线性概率等密码性质。小规模S盒选用8 bit置换，根据图1 描述的大规模S 盒可以构造一系列具有相同优良密码学性质的32 bit S 盒。

同理，考虑到线性置换循环移位等价性质，与置换P5和P6等价的线性置换如表3 所示。

表3 线性置换P5 和P6 的等价类

根据线性置换循环移位数的等价性质，即=(ti+16)mod64,i=1,…,5，可知属于相同等价类的线性置换构造的64 bit S 盒具有相同的最大差分和线性概率等密码性质。小规模S 盒选用3.1 节构造的16 bit 置换，根据图1 描述的大规模S 盒可以构造一系列具有相同优良密码学性质的64 bit S 盒。

4 实例分析

4.1 16 bit 大规模S 盒

对于线性变换P2(x) =x⊕ (x＜＜＜ 4) ⊕ (x＜＜＜7) ⊕ (x＜＜＜ 11) ⊕ (x＜＜＜15)，采用2 轮SPS 结构可以有效生成密码学性质优良且实现代价低廉的16 bit S 盒。

1) 为便于与现有结果比较，采用与Piccolo 算法相同的 4 bit S 盒S={10,2,8,6,12,15,7,1,3,11,14,13,0,5,4,9}，使用线性置换P2(x)，按照图1所示的SPS 结构构造16 bit S 盒S1，其密码学性质如下：差分均匀度为Diff(S1)=96，最大差分概率为，线性度为Lin(S1)=3 200，最大线性概率为；硬件流水线实现时，P2(x)共需要4 个异或运算和4 个循环移位，由于比特之间的异或运算大约需要2 个逻辑门电路，而循环移位靠拉线实现，不占资源，一个4 bit S 盒大约需要 30 个逻辑门电路，因此共需要16×4×2+30×8=368 个逻辑门电路；软件实现时，仅需要一次查表。

NBC 算法采用Galois 结构的16 级NFSR 构造16 bit S 盒S3，寄存器每迭代一拍，除常规移位外每拍以非线性方式更新4 bit，每拍有8 个异或运算，4 个与运算以及一个与非运算，共迭代20 拍。该16 bit S 盒S3的密码学性质如下：差分均匀度为 Diff(S3)=22，最大差分概率为，线性度为Lin(S3)=3 144，最大线性概率为；硬件流水线实现时，S3共需要20×(8×2+4×1.25+1×1)=440 个逻辑门电路；软件实现时，仅需要一次查表。

与有限域上的MDS 矩阵乘法运算及Galois 结构的16 级非线性移位寄存器运算相比，该类大规模S 盒的运算代价更加低廉，密码学指标更优，密码学性质对比如表4 所示。

表4 16 bit S 盒S1、S2 及S3 密码学性质对比

2) 通过挑选4 bit 最优S 盒，结合上述线性置换P2(x)，可以构造密码学性质更优的16 bit S 盒。考虑到差分和线性性质达到最优4 bit S 盒分别属于16 个仿射等价类[32]，通过在这些最优4 bit S 盒等价类代表元中选择S 盒进行测试，得到一系列16 bit S 盒。其构造参数及密码性质如表5 所示。

由表5 可见，通过该方式构造的系列16 bit S 盒的密码性质优良且较为稳定，其最大差分概率集中分布在区间[2-9.83,2-8.64]，最大线性概率集中分布在区间[2-8.71,2-8]。与现有的Piccolo 算法S 盒相比较，通过本文方法可以得到更优密码学性质的16 bit S 盒，其4 bit S 盒S={2,0,1,8,3,11,6,7,4,9,10,15,12,13,14,5}和线性置换P2(x)构造，其密码学性质如下：最大差分概率2-9.83，最大线性概率2-8.71。该S 盒具有更均衡的抗差分和抗线性攻击能力。

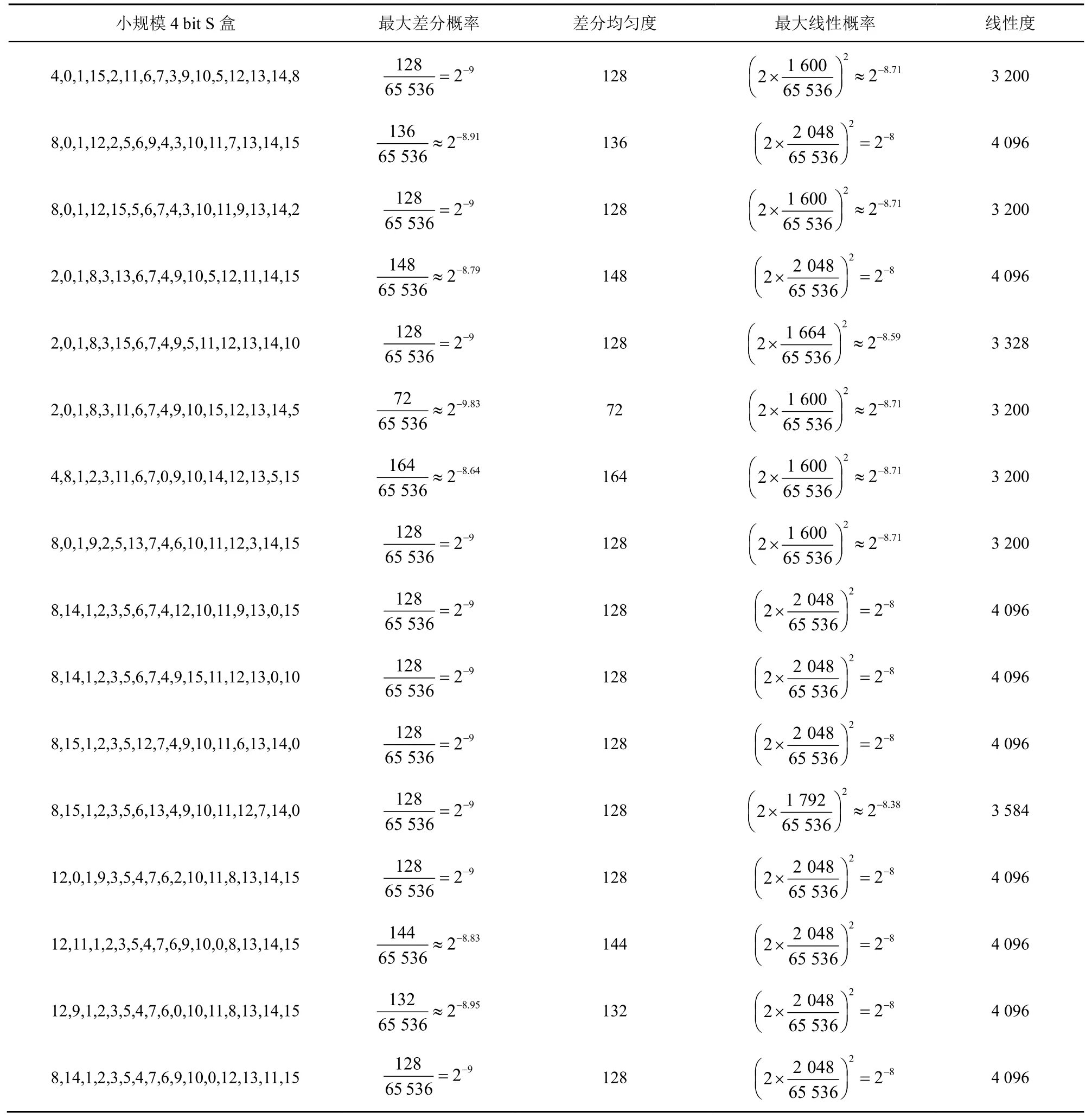
表5 2 轮SPS 结构构造的大规模S 盒密码学性质

4.2 32 bit 大规模S 盒

对于最优线性变换P3(x)或P4(x)，采用2 轮SPS结构可以有效生成密码学性质优良且实现代价低廉的32 bit 大规模S 盒。为了降低资源占用，这里8 bit S 盒可考虑使用4 bit 小规模S 盒（t1、t2及t3）通过3 轮平衡Feistel 结构构造得到，如图2 所示。其中，选用4 bitti（i=1,2,3）盒的最大差分概率与最大线性概率均为2-2，即Diff(ti)=4，Lin(ti)=8，，使8 bit 小规模S 盒的差分概率p≤2-4.67，线性概率q≤2-4。基于此类线性置换采用SPS 结构可以有效构造密码学性质优良且软硬件实现代价低廉的32 bit S盒。其密码学性质如下。

由引理2 可知，2 轮SPS 结构构造的32 bit 大规模置换S 盒的差分概率上界为pd-1；由引理3 可知，2 轮SPS 结构构造的32 bit 大规模置换S 盒的线性概率上界为qd-1。

1) 差分均匀度Diff(S)=104，最大差分概率为

2) 线性度为 Lin(S)=224，最大线性概率为

3) 硬件流水线实现时，P3(x)或P4(x)共需要4 个异或运算和4 个循环移位，由于比特位之间的异或运算大约需要2个逻辑门电路，而循环移位靠拉线实现，不占资源，如图2 所示的8 bit S 盒需要3 个4 bit 异或运算和3 个4 bit T 盒运算，因此，共需要32×4×2+8×(3×4×2+3×30)=1 168 个逻辑门电路。

图2 3 轮平衡Feistel 结构构造的8 bit S 盒

SPRING 算法[10]的32 bit S 盒迭代32 拍，每拍需要4 个移位寄存器和4 个反馈函数运算，移位寄存器共需要32×6=192 个逻辑门电路，反馈函数需要4×2×2+6=22 个逻辑门电路，一拍S 盒共需要192+22=214 个逻辑门电路。由于一轮S 盒迭代32 拍，硬件流水线实现共需要32×214=6 848 个逻辑门电路。与SPRING 算法的32 bit S 盒相比，采用2 轮SPS 结构构造的32 bit S 盒有更优的密码学性质，如表6 所示。

表6 32 bit S 盒密码学性质对比

4.3 64 bit 大规模S 盒

对于最优线性变换P5(x)或P6(x)，采用2 轮SPS结构可以有效构造密码学性质优良且实现代价低廉的64 bit 大规模S 盒。为了降低资源占用，这里的16 bit S 盒可考虑使用4 bit 小规模S 盒通过图1的2 轮SPS 结构构造得到，如图3 所示，其中选用的4 bitt（ii=4,5,…,11）盒的最大差分概率与最大线性概率均为2-2，即Diff(ti)=4，，Lin(ti)=8，，使16 bit 小规模S 盒的最大差分概率p≤2-9.83，线性概率q≤2-8.71。基于此类线性置换采用SPS结构可以有效构造密码学性质优良且软硬件实现代价低廉的64 bit S 盒。其密码学性质如下。

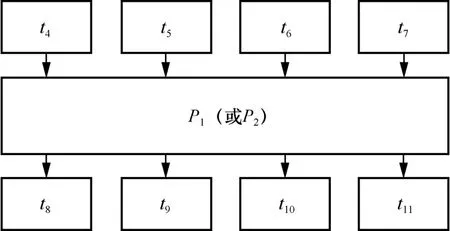
图3 2 轮SPS 结构构造的16 bit S 盒

由引理2 可知，2 轮SPS 结构构造的64 bit 大规模置换S 盒的差分概率的上界为pd-1；由引理3可知，2 轮SPS 结构构造的64 bit 大规模置换S 盒的线性概率的上界为qd-1。

1) 差分均匀度为Diff(S)=724，最大差分概率为

2) 线性度为Lin(S)=3 2004，最大线性概率为

3) 硬件流水线实现时，P3(x)或P4(x)共需要4 个异或运算和4 个循环移位，由于比特位之间的异或运算大约需要2 个逻辑门电路，而循环移位靠拉线实现，不占资源，2 轮SPS 结构构造的16 bit S 盒如图3 所示。16 bit S 盒约需要368 个逻辑门电路，因此共约需要64×4×2+8×368=3 456 个逻辑门电路。

Alzette 算法[14]的64 bit S 盒迭代4 轮，每轮包含一个32 bit 整数加法运算、2 个32 bit 异或运算及2 个32 bit 循环右移运算，一个32 bit 整数加法运算最多需要200 个逻辑门电路，2 个32 bit异或运算约需要2×2×32=128 个逻辑门电路，循环移位拉线实现不占资源，因此该64 bit S 盒流水线硬件实现共需要4×(200+128)=1 312 个逻辑门电路。与Alzette 算法的64 bit S 盒相比，采用2 轮SPS 结构构造的64 bit S 盒有更优的密码学性质，如表7 所示。

表7 64 bit S 盒密码学性质对比

5 结束语

本文基于循环移位与异或运算构造了有限域上分支数最佳的一类线性变换P，给出了该类最优线性变换的一种新的证明方法，建立了2 轮SPS 结构的大规模S 盒模型，通过小规模S 盒与最优循环移位-异或型线性变换，设计了一系列密码学性质优良的轻量级大规模S 盒。该设计方案仅使用查表、循环移位、异或三类基本运算，提高了大规模S 盒的线性度和差分均匀度，与已有大规模S 盒构造方法相比，本文大规模S 盒设计方案运算代价更加低廉，其差分、线性等密码学性质更加优良，可应用于对称密码算法非线性置换的设计。