基于改进A*算法的多AGV路径规划研究

官祥锦，陈 娟，张为民

（1. 北京化工大学，北京 100029；2. 中国航空制造技术研究院，北京 100024）

AGV在工业生产和物流领域扮演着越来越重要的作用，能够有效地改善工业生产和生活的运输系统结构，将人力从繁琐重复的体力劳动中解放出来，不仅大大地降低了生产成本，也提高了生产效率[1]。而多AGV的路径规划和无碰撞调度是AGV应用面临的两大问题[2–3]，其在环境复杂的工业现场和生产车间尤为突出。根据是否已知全局路径信息，可将AGV路径规划分为全局路径规划和局部路径规划。全局路径规划是指AGV在行驶前已经掌握了全局的路径信息，包括AGV的位置信息、所处环境的障碍物信息以及可行驶的路径信息，然后根据掌握的全局信息规划出一条从起点到终点的最优路径；局部路径规划是指AGV在行驶前对环境信息一无所知或知道部分环境信息，需要在行驶的过程中实时动态地了解自身的位置和环境信息，然后通过掌握的环境信息规划出一条从起点到终点的最优路径。目前应用于全局路径规划的算法主要有：栅格法（其中最具代表性的是A*算法[4]、D*算法和Dijkstra算法[5–7]）、快速搜索随机树法[8]（Rapidlyexploring random tree，RRT）、Voronoi图法等。应用于局部路径规划的算法主要有：人工势场法[9]、动态窗口法（Dynamic window approach，DWA），以及一些智能算法（其中主要有模糊算法、遗传算法[10]、神经网络、粒子群算法[11]、蚁群算法等）[12–15]。由于计算的复杂度以及现实生产环境的限制，且大多工业生产和物流环境是全局已知的，所以在实际的AGV路径规划中，局部路径规划算法和智能路径规划算法应用的较少，大多还停留在仿真研究阶段，并没有应用到实际的生产生活中。

A*算法由于其算法简单，在中小型地图中具有良好的搜索性能，是当前AGV进行路径规划时应用的最广泛的算法。但传统的A*算法存在需要搜索的节点数多、路径转角多、生成的路径平滑度低等问题[16]，这些问题在多AGV同时进行路径规划时尤为突出，特别是当多辆AGV存在路径冲突或者已规划好的路径上出现障碍物，需要对其进行重规划时，搜索的节点数将大大增加，降低了重规划的效率。针对传统A*算法存在的问题，Song等[17]做了很多研究，但大都是根据特定的应用环境进行的改进与研究。余星宝等[18]采用传统A*算法找出最短路径上转弯处的特征点，再利用四阶贝塞尔曲线对转弯处的特征点进行平滑处理，得到1条无碰撞、平滑度高、具有一定曲率，且相对距离更短的路径，解决了传统A*算法生成的路径转角多、平滑度低、易发生碰撞的问题。但该方法对于只能沿着已铺设路径引导线行走的AGV不实用。胡蔚旻等[19]以传统A*算法为基础，引入3轴–2象限、AGV路径转向数来删除路径上的无效备选点，从而使AGV的行驶路径得到有效的平滑。但该算法在多辆AGV发生路径冲突时，不能对其路径进行动态调整，所以不适用于对多辆AGV进行路径规划的情况。刘生伟等[20]在传统A*算法启发函数的基础上，引入了父节点的启发函数值，对当前节点和父节点启发函数之和进行加权处理，并通过判断转折点的方式，删除多余的冗余节点，使得规划出的路径更加平滑。该算法和传统的A*算法及指数衰减加权改进A*算法相比，在搜索时间、路径长度以及路径包含的节点数上都有所减少。然而本文所使用的八邻域搜索方式，对于已铺设引导线的AGV来说并不实用。余文凯等[21]将环境信息和AGV位置信息融入到评价函数中，并使用障碍率和直通率给A*算法的评价函数进行加权处理。通过基于K-Means聚类算法对栅格地图进行分区预处理后，再使用改进的A*算法搜索最短路径。对搜索到的最短路径，使用改进的Floyd算法对路径进行双向平滑度优化处理，并添加防碰撞安全距离系数，有效地增加了路径的平滑度和安全性。但该算法仅考虑单辆AGV的情况，并且对规划出的路径进行平滑处理的方式不适用于已铺设路径引导线线的AGV。卞永明等[22]根据AGV从起点到当前点发生的转弯次数，对A*算法的启发函数进行奖励和惩罚，可以显著地降低转弯次数，但该算法没有考虑一条直线上的多余冗余节点。吴飞龙等[23]将AGV的位置信息和环境信息融入到了A*算法的启发函数中，并使用环境的混乱程度和障碍率对启发函数进行加权处理，删除路径中多余的转折点和冗余节点，使AGV规划出的路径更加平滑。陆佳依等[24]采用分裂和筛选的方案对传统A*算法进行优化，通过在未搜索节点的启发函数中增加转弯权值，在路径规划过程中考虑转弯带来的消耗，缩短了路径的总长度，减少了AGV的转弯次数。该方法明显提高了A*算法的复杂度，降低了搜索效率。

现有的AGV路径规划算法，考虑的情况大都比较理想化，没有对AGV的行驶方向做约束，导致在使用A*算法对AGV行驶路径进行规划时，既可以四方位搜索，也可以八方位搜索，从而出现规划的路径只要存在空白区域就可随便转弯的情况。这对于重载AGV以及对生产安全要求极为严格的工业生产现场来说是不现实的，在对AGV进行路径规划的过程中，如果不对AGV的行驶方向做约束，直接按照规划出的路径行驶，将非常容易和障碍物发生碰撞，发生安全事故。并且当涉及多辆AGV同时运行时，出于工业生产安全的考虑，对AGV的路径规划要求将变得更加严苛。此时，安全是路径规划优先考虑的问题，所以在进行多AGV路径规划时，需尽量将多AGV发生冲突碰撞的概率降到最低，其次才是AGV路径最优的问题，这种情况下，单纯地使用A*算法将不再满足路径规划要求。当涉及多辆AGV时，AGV在运行的过程中，彼此互为障碍物，并且障碍物在实时移动，此时的AGV路径规划问题将从1个静态路径规划问题转变为1个动态路径规划问题。邢普学等[25]通过增加AGV共享路径的惩罚值对A*算法进行改进，结合改进的A*算法设置了碰撞解决规则，能够解决AGV的碰撞问题，但是该规则在AGV发生路径冲突时，只考虑对其进行重规划，重归化后的路径可能会导致新的碰撞出现及多AGV死锁的发生。泰应鹏等[26]通过结合A*算法和时间窗模型，对多AGV进行了动态路径规划，通过提前计算AGV经过每个节点的时间，对时间窗进行动态的排布和更新，并为多辆AGV动态地分配优先级，实现了无冲突，无重复的系统调度。但是在实际中，准确计算每辆AGV到达每个节点的时间是困难的，如果发生较大的时间计算偏差，将容易导致AGV发生碰撞问题。廉胤东等[27]将当前节点到相邻候选节点的期望运行时间加入到传统A*算法的启发函数中，对传统A*算法进行了改进，在改进A*算法的基础上，对AGV下一个运行位置进行预判，实现AGV的冲突避让，提高了AGV路网资源的利用率。但该算法也存在计算量大，对AGV系统要求较高等问题。高新浩等[28]基于改进时间窗的两阶段动态路径规划算法，构建环境拓扑地图，使用A*算法实现AGV离线路径规划。通过动态环境拓扑地图，使用BP神经网络实现AGV路径的动态规划，降低了多AGV在行驶过程中发生冲突和碰撞的可能性。但是该算法会随着AGV的频繁调度和重规划，以及环境地图的扩大而增加计算复杂度，降低AGV路径搜索效率。

基于以上问题，本文以铺设AGV导引线的工业生产现场为背景，提出了一种改进的A*算法，该算法使用切比雪夫距离对当前节点的启发函数进行加权处理，在相同的地图环境下，相比于Dijkstra算法，传统A*算法以及已有的使用切比雪夫距离对当前节点和父节点的启发函数进行加权的方法，其搜索节点数和搜索时间得到了有效的降低，显著地提高了A*算法在进行重规划时的搜索效率。在改进A*算法的基础上，结合时间窗模型，通过对每辆AGV的行驶节点进行提前预判，动态调整AGV的优先级，有效地解决了多AGV路径规划时的冲突问题，在AGV遇到其他车辆需要进行避让或重规划时，通过比较避让预计增加的时间和重规划预计增加的预估时间，并选择预计增加时间少的方案解决多AGV路径规划时的死锁以及路径冲突问题。采用该算法既可以让AGV得到了相对最优路径，也有效地解决了多AGV在运行过程中的时间、空间冲突问题。该算法增加的算法复杂度小，通过试验证明，此方法在对多AGV进行路径规划时，搜索速度快、实时性较好。

1 改进A*算法

A*算法是从Dijsktra算法发展而来的，是一种启发式搜索算法。它利用启发信息来指导路径的搜索，以实现减少搜索范围和降低搜索问题的复杂度。同时，也是静态路网中搜索最短路径时最有效的直接搜索方法。在A*算法中，估计值（即启发函数h（n）值）与实际距离值越接近，A*算法的搜索速度越快，搜索效率也就越高。由于A*算法在中小型地图中搜索的高效性，在实际中得到了广泛的应用。但是传统的A*算法由于其搜索路径时需要遍历的节点数多，且规划出的路径存在过多的冗余节点和转折点，所以很多学者对传统的A*算法进行了改进。传统的A*算法为

式中，n为当前节点；f（n）为从起始节点经过当前节点n到达目标节点的最小代价估计；g（n）为起始节点到当前节点的最小代价估计；h（n）为当前节点n到目标节点的最小代价估计，也称为启发函数。

启发函数h（n）在A*算法中起着至关重要的作用。这里设当前点到目标点的实际代价为Q。当h（n）=0时，A*算法将变成Dijkstra算法，Dijkstra算法能够保证找到一条最短路径；当h（n）Q时，A*算法在寻找最佳路径的过程中会扩展别的任何一个节点，这种情况下不能够保证找到一条最短路径。根据以上原则，为了能够得到一条从起点到终点的最短路径，要保证h（n）≤Q，并且h（n）越逼近Q值，其搜索速度会越快。这也是对A*算法进行改进的重要思路。

A*算法中h（n）常用曼哈顿距离、欧几里德距离、欧几里德距离的平方表示。欧几里德距离的表示方式为

曼哈顿距离的表示方式为

切比雪夫距离的表示方式为

式（2）～（4）中，（xe，ye）为终点坐标； （xn，yn）为当前点n的坐标。

由于传统A*算法在搜索路径时需要遍历的节点数和生成路径中的冗余节点较多，且在地图较大时尤为突出，严重影响了A*算法的搜索效率。本文遵循启发函数h（n）越逼近当前点到目标点的实际代价值Q，其搜索速度会越快的原则，对A*算法进行了改进。

从式（2）～（4）可得，对于∀n和∀e有

也即，ho≤hm。也即，hc≤hm。

也即，hc=|xe–xn|≤ho

从式（5）、（6）和（9）可以得到

由于本文所涉及的工业环境已经铺设了AGV路径导引线，AGV不能沿着任意角度移动，只能沿着网格的方向移动。欧几里德距离ho表示的是对角线距离，对于本文已铺设引导线的AGV不适用。本文使用取值更接近实际代价Q的曼哈顿距离hm作为启发函数，并使用切比雪夫距离hc对启发函数hm进行加权，改进后的A*算法为

改进后的A*算法可以减少在路径搜索时需要遍历的节点数，提高搜索效率。

A*算法需要维护一个Open表和一个Close表，Open表中记录了所有已经遍历过但是没有被考察的节点；Close表中记录了所有已经考察过的节点，初始化时Open表中记录了起始节点，Close表为空。执行A*算法时，从起始节点开始，不断地向外扩充，并维护和更新Open表和Close表，直到终点加入Close表为止。改进后的A*算法流程如图1所示。

图1 改进A*算法流程图Fig.1 Flow chart of improved A* algorithm

本文以实际的工业生产制造车间为背景，利用栅格法和拓扑图法对工业生产制造车间的平面图进行电子地图的构建，图2为实际工业生产制造车间平面图，圆形数字标识的点为AGV的运输站点，其他数字标识的点为AGV路径上的节点。图3为与图2相对应的使用栅格法构建的电子地图。

图2 工业生产车间平面图Fig.2 Floor plan of industrial production workshop

图3中的栅格地图大小为20×42，横坐标范围[0，41]、纵坐标范围[0，19]。栅格地图中的每个数字点代表着生产车间的一个站点，其中站点1和17是AGV的车库和充电桩所在位置。由于使用栅格地图规划出的AGV路径存在冗余的节点，因此本文对使用改进A*算法在栅格地图下得到的路径做进一步处理，删除生成路径上不必要的冗余节点，使最终规划出的路径需要保留的节点数更少。

为了验证本文提出的改进A*算法的有效性，分别对Dijkstra算法、传统A*算法、Tang等[16]提出的改进的A*算法和本文提出的改进的A*算法进行仿真试验对比。以图3的栅格地图为试验地图，每次试验分别以栅格地图中的每个站点为起点或终点，经排列组合每次共验证378条路径。共做10次试验，最后取10次的平均值。试验结果及其对比如表1和表2所示。

表1 4种路径规划算法遍历节点数和平均搜索时间对比Table 1 Comparision of the number of traversed nodes and the average search time of four path planning algorithms

表2 本文改进A*算法相较其他3种算法遍历节点数和平均搜索时间减少百分比Table 2 Compared with the other three algorithms, the improved A*algorithm in this paper reduces the number of nodes traversed and the average search time by a percentage %

图3 工业生产车间栅格地图Fig.3 Raster map of industrial production workshop

从试验结果可以得出，与Dijkstra算法、传统A*算法和Tang等[16]提出的改进的A*算法相比，本文提出的改进A*算法的平均搜索时间和平均遍历节点数得到了显著的减少，搜索效率得到了显著的提高。与Dijkstra算法相比，平均搜索时间和平均遍历节点数分别减少了74.95%和67.87%；与传统A*算法相比，平均搜索时间和平均遍历节点数分别减少了59.91%和20.81%；与Tang等[16]提出的改进的A*算法相比，平均搜索时间和平均遍历节点数分别减少了17.57%和8.00%。使用改进的A*算法规划从节点1（坐标（2，1））到节点14（坐标（22，11））的路径如图4所示。

图4中x轴代表栅格点的横坐标；y轴代表栅格点的纵坐标，其中曲线上的每个点代表规划出的路径需要经过的每个节点。从图4中可以看出，使用改进的A*算法规划出的路径需要保存的节点为32个，本文在规划出的原始路径基础上做了进一步处理，删除路径中冗余的节点后，路径需要保留的节点数仅剩5个，路径也变得更加光滑。

图4 使用改进A*算法规划的从节点1到节点14的路径Fig. 4 Using the improved A* algorithm to plan the path from node 1 to node 14

2 多AGV无碰撞规划

工业生产车间常存在多个站点以及多个生产任务，需要多辆AGV同时进行无碰撞协调运行，所以需要对多辆AGV的行驶路径进行合理规划，在保证不发生碰撞的基础上，使每辆AGV的行驶路径最优。由于多辆AGV在行驶的过程中互为障碍物，所以需要考虑多辆AGV在行驶过程中的动态规划问题，保证每段路上在同一时间只能有1辆AGV通过。只有合理的规划和协调好AGV行驶路径的空间和时间资源利用问题，才能保证多辆AGV有条不紊地运行。

2.1 多AGV冲突类型

当多辆AGV同时运行时，AGV之间主要存在路径不冲突、路径冲突但时间不冲突、相向冲突、节点冲突4种情况。

（1）路径不冲突。当多辆AGV之间规划的路径不存在重合节点和交叉节点，也即路径不存在冲突时，每辆AGV可各自独立运行，不需要考虑碰撞问题。

（2）路径冲突时间不冲突。当多辆AGV之间存在路径冲突，但是时间不冲突时，因为在同一节点或同一路段上行驶的时间没有交叉和重叠，每辆AGV可独自运行，不需要考虑碰撞问题

（3）相向冲突。如图5所示，当两辆AGV同一时间在同一条路段上相向行驶时，会产生相向冲突。此时需要采用相应的碰撞预测方法和策略，解决多辆AGV同一时间在同一路段上的相向冲突问题。

图5 AGV路径发生相向冲突Fig.5 AGV conflicts in same direction

（4）节点冲突。如图6所示，当多辆AGV同一时间在交叉路口相遇时，会产生节点冲突问题，此时也需要采用相应的碰撞预测方法和策略解决该问题。

图6 AGV路径发生节点冲突Fig.6 AGV conflicts in same node

2.2 基于时间窗的冲突解决方案

在AGV路径规划中，时间窗是指AGV从进入某路段到离开该路段所占用的时间段。可以将某路段的时间窗划分为空闲时间窗和占用时间窗。空闲时间窗为该路段空闲的时间段，在空闲时间窗内任何一辆AGV都可在该路段上行驶；占用时间窗为当前AGV在该路段行驶占用的时间段，在占用时间窗内其他车辆不能驶入该路段。时间窗模型的示意图如图7所示。

图7 时间窗模型Fig.7 Time window model

这里设AGV路径上的每个节点都用相应的坐标（x，y）表示，（x1，y1）—（x2，y2）表示路径上2个节点（x1，y2）和（x2，y2）之间的路段。图8为两辆AGV在路段（2，9）—（2，13）上发生相向冲突的情况。图9为两辆AGV在节点（2，13）发生节点冲突的情况。

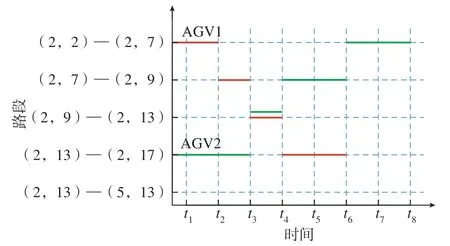
图8 两辆AGV发生相向冲突时间窗Fig.8 Two AGVs conflict time window in the same direction

图9 两辆AGV发生节点冲突时间窗Fig.9 Two AGVs conflict time window in the same node

所有AGV在路段k上的时间窗模型可以表示为

式中，T（k）为所有AGV在路段k上的时间窗集合；i表示第i辆AGV；n表示AGV的数量。

根据式（12）可以得到所有AGV在所有路段上的时间窗集合，为

式中，Tm表示所有AGV在路段m上的时间窗集合；m表示AGV规划出的路径的路段数；n表示AGV的数量。式（13）中的每一列代表每一辆AGV在所有路段上的时间窗集合。

多辆AGV在路段k上发生相向冲突的时间窗模型为

式中，t′ik为第i辆AGV进入路段k时的时间；t″ik为第i辆AGV离开路段k时的时间；tqk为第q辆AGV在路段k上的时间窗。即当两辆AGV在同一路段k上的时间窗发生重叠时，AGV将发生相向冲突。

当多辆AGV同时在某一节点的相邻路段上行驶，并且同时到达该节点时，将发生节点冲突，节点冲突的时间窗模型为

式中，t″ik为第i辆AGV离开路段k时的时间；t″qp为第q辆AGV离开路段p时的时间。路段k和路段q有相同的节点，并且k，q∈[1，m]。即多辆AGV同时离开不同的路段，到达同一个节点时将发生节点冲突。

从图8和9的相向冲突及节点冲突的时间窗中可以看出，将时间窗右移是解决多AGV路径冲突的主要方法。本文在每辆AGV行驶过程中，提前对AGV路径上的3个节点进行时间窗的更新和排布，当检测到时间窗有冲突时，根据生产任务需求以及当前AGV离终点的远近程度动态调整相应AGV的优先级，让优先级低的AGV进行路径重规划或避让，即让其在冲突路段上的时间窗右移，从而避免AGV产生路径上的冲突与碰撞。在重规划或避让策略的选择上，可以通过式（16）进行选择。

式中，Δtr表示AGV进行重规划预计需要增加的行驶时间；Δte表示AGV进行避让等待预计需要增加的行驶时间。

多AGV无碰撞规划流程如图10所示。

图10中节点标志g表示该节点既没有AGV占用也不是AGV规划路径中的节点。节点标志y表示该节点是AGV路径规划中需要经过的节点，但是现在AGV还没有经过该节点。节点标志r表示该节点是AGV路径规划中需要经过的节点，并且当前AGV离该节点的距离在3个节点以内。

图10 多AGV无碰撞规划流程图Fig.10 Flow chart of multi-AGV collision-free planning

3 试验结果与分析

为了验证本文提出的改进的A*算法以及多AGV无碰撞规划策略的有效性，使用Visual Studio 2017+Qt5进行编程，将改进的算法及策略应用到实际工业生产AGV上。AGV长2 m、宽90 cm、高60 cm、载重1500 kg，其中AGV自带车载工控机用于AGV的控制，现场的AGV通道为单行道，即同一时间只允许有1辆AGV通过。出于工业现场安全考虑，AGV在运输过程以0.5 m/s的速度匀速行驶。AGV原型图如图11所示。

图11 AGV原型Fig.11 AGV prototype

在图12中，AGV1从1号站点到17号站点；AGV2从8号站点到19号站点。图13为相对应的时间窗模型。使用改进的A*算法规划出的路径不存在重合和交叉的节点，所以两辆AGV无需考虑路径冲突问题，在图13中对应的时间窗上也不存在重叠情况。

图12 两辆AGV路径无冲突Fig.12 No conflict between two AGVs

图13 两辆AGV路径无冲突时间窗Fig.13 Two AGV conflict-free time window

在图14中，AGV1从t1时刻开始，从17号站点到10号站点；AGV2从t4时刻开始，从8号站点到20号站点。图15为相对应的时间窗模型。使用本文提出的改进的A*算法规划出的路径存在重合和交叉的节点，从图15时间窗模型中可以得出，AGV1和AGV2在路段（2，39）—（2，32）和（12，32）—（2，32）交叉位置将发生节点冲突，所以根据AGV的优先级情况，AGV2将会在（2，37）节点选择等待避让，待AGV1经过（2，32）节点后，AGV2再按照原规划路径行驶到20号站点。

图14 两辆AGV在节点（2，32）发生节点冲突Fig.14 Two AGVs have a node conflict at coordinates (2,32)

图15 两辆AGV在节点（2，32）发生节点冲突时间窗 （避让等待）Fig.15 Time window when two AGVs have node conflict at coordinates (2,32) (Waiting)

在图16中，AGV1从t1时刻开始，从1号站点到16号站点；AGV2从t1时刻开始，从9号站点到2号站点。图17为相对应的时间窗模型。使用本文提出的改进的A*算法规划出的路径存在重合和交叉的节点，规划出的AGV1原始路径为（1，2）→（2，2）→（2，32）→（12，32）→（12，39）→（13，39）。从图17时间窗模型中可以得出，AGV1在节点（2，17）位置检测到前向路径上的节点被占用，根据AGV的无碰撞规划策略，AGV1选择以节点（2，17）为新节点，终点不变，重新进行路径规划，AGV1重规划后的路径为：（2，17）→（2，13）→（12，13）→（12，39）→（13，39）。AGV2的路径保持不变，从而避免两辆AGV发生路径冲突碰撞。

图16 两辆AGV在节点（2，17）发生相向路径冲突Fig.16 Two AGVs have a same direction conflict at coordinates (2,17)

图17 两辆AGV在节点（2，17）发生相向冲突时间窗（重规划）Fig.17 Time window when two AGVs have a same direction conflict at coordinates (2,17)

本文以Visual Studio 2017+Qt5为开发环境，在图11所示的AGV上进行了试验验证。表3和4分别对应图12、14和16中，两辆AGV没有路径冲突、发生相向冲突（避让等待）和发生相向冲突（重规划）时进行路径规划消耗的时间，并在4种路径规划算法上进行了验证和对比分析。

表3 AGV1路径规划消耗时间（不包括AGV运行时间）Table 3 AGV1 path planning consumption time(not including AGV driving time) s

从以上试验可以看出，本文提出的改进A*算法与多AGV路径规划策略结合，在多AGV无路径冲突，以及存在节点或路径相向冲突时，能够得到较好的无碰撞规划结果，能够有效地解决实际工业生产过程中多AGV同时行驶时的路径冲突问题。当某辆AGV出现故障，长时间占用某条路径时，调度系统会检测到故障并产生报警，通知工作人员进行处理，同时调度系统会将电子地图中的该栅格点置为障碍物点，其他AGV进行路径规划时将不会再考虑该条路径。从表3和4中可以看出，相较与Dijkstra算法、传统A*算法和Tang等[16]提出的改进A*算法，使用本文改进的A*算法，无论是在两辆AGV没有路径冲突或者发生路径冲突时，都能够很快地对每辆AGV进行路径规划，能够较好地满足实时性要求。

表4 AGV2路径规划消耗时间（不包括AGV运行时间）Table 4 AGV2 path planning consumption time(not including AGV driving time) s

4 结论

本文以实际工业生产现场为背景，研究了多AGV路径规划算法和无碰撞策略。通过使用切比雪夫距离对启发函数进行加权，对传统的A*算法进行了改进，同时，通过时间窗模型和动态调整AGV的优先级，解决了多AGV的路径冲突问题，具有较好应用价值。试验表明，本文提出的改进的A*算法显著地降低了AGV在进行路径规划时的路径搜索时间，提高了搜索效率，实时性也得到了进一步的提高。