端部非镦粗高强度钢拉杆节点设计及试验研究

黄山，李超群，王炜萍，张杰，余佳远

（1.中天建设集团有限公司，浙江 杭州 310008；2.浙江中天恒筑钢构有限公司，浙江 杭州 310008）

0 引言

核心筒-钢桁架-悬挂结构是以内部核心筒为竖向承重结构，顶部钢桁架作为水平转换结构，楼面结构通过高强度钢拉杆悬挂于顶部钢桁架结构上而形成的一种新型结构体系[1]。该结构体系采用的高强度钢拉杆抗拉强度大，构件截面面积小，有效降低整体结构自重的同时易于满足建筑功能要求，并增加了建筑实际使用面积，其综合效益高，所以近年来核心筒-钢桁架-悬挂结构越来越多地被使用于实际建筑结构当中。

但设计阶段，通常要求钢拉杆杆体与连接节点等强，故其端部往往要求采用局部锻造镦粗后进行螺纹加工。其中，梁秀春提出了一种镦粗大高径比锻件方法对棒料进行局部头部镦粗[2]；陈卫铭采用了多道次镦粗方式对棒料进行了局部成形[3]；陈孝学等使用了棒料连续镦粗的成形工艺[4]，而镦粗过程中的锻造比、镦粗长径比、始终锻温度、加热时间、镦粗次数等[5]工艺参数的控制难度大，加工步骤多，最终造成钢拉杆制作成本高企且端部成型质量不易保证。本文通过对高强度钢拉杆端部节点理论计算分析并在此基础上加以试验验证，最终得到端部非镦粗钢拉杆完全能满足设计要求，降低了工程造价，节约了制作工期。

1 工程概况

某工程由A、B、C 三幢高层建筑构成且均采用核心筒-钢桁架-悬挂结构受力体系，具体传力路径较为明确：楼层钢梁—钢拉杆—顶部钢桁架—核心筒—基础。该三幢高层建筑主体结构顶标高均为57.00m，地下3 层，地上13 层，其中，B3～L4层为框架混凝土结构，部分梁柱为组合结构，内置劲性梁和劲性柱；L5～L13 层为钢结构，其竖向受力构件为高强度钢拉杆，标准层层高4.2m；顶部桁架层为双向设置的转换桁架，其中部穿过混凝土核心筒，外圈悬挑端与高强度钢拉杆相连。具体结构效果如图1 所示。

图1 效果图

本工程钢结构材质均为Q355B（钢拉杆除外），其中核心筒劲性梁以及劲性柱的规格为：H 200×200×20×20～H 400×200×30×30；外框钢梁规格为：H 400×150×8×10～H 700×300×14×25、口 300×450×20×20～口 400×450×30×30。外框竖向受力构件采用的高强度钢拉杆具体型号为ZL 型[6]，直径为120mm，其中L12层～L13层的钢拉杆材质等级为835级，其余位置处均采用650 级，套筒材质等级与钢拉杆材质相适应。外框钢梁通过外环板节点支撑于支撑套筒上，支撑套筒与调节套筒通过螺纹连接，调节套筒与高强度钢拉杆通过螺纹连接，具体组装图如图2 所示。

图2 钢拉杆组装图

2 端部非等强钢拉杆螺纹设计

根据设计要求，835 级钢拉杆的设计承载力不得低于8 500kN，而由钢拉杆组装图可知，钢拉杆各部件通过螺纹进行连接，故其承载力取决于杆体本身强度以及螺纹连接强度[7]。由于本工程高强度钢拉杆采用端部非镦粗工艺，杆体本身螺纹处的有效直径较杆体中部有一定削弱，最终钢拉杆承载力取决于端部有效截面的应力大小、杆体螺纹以及调节套筒的连接强度。

2.1 钢拉杆有效截面处的应力

钢拉杆直径为120mm，对应螺纹规格为M118X6 普通螺纹，螺距6mm。螺纹根部的有效工作直径为：

钢拉杆螺纹处有效截面面积为：

钢拉杆有效截面处的应力大小：

其中P为螺纹螺距，d为螺纹外径，[σ]为许用正应力，F为设计承载力。将具体数值代入可得钢拉杆有效截面处的应力为803.3MPa≤[σ]。

2.2 调节套筒有效截面处的应力

调节套筒外径200mm，最大内径130mm，外径螺纹规格为M195X8，如图3 所示。调节套筒的有效外径为：

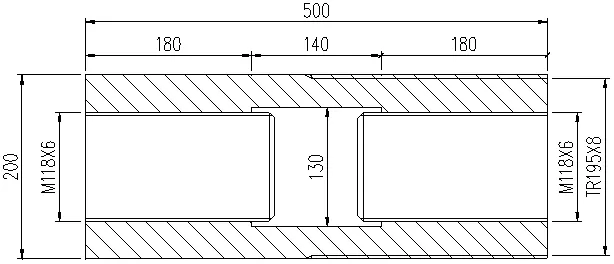
图3 调节套筒组装图

套筒最不利处有效截面面积为：

套筒最不利处有效截面应力大小：

其中P为螺纹螺距，d为螺纹外径，d'为调节套筒内径，[σ]为许用正应力，F为设计承载力。将具体数值代入可得调节套筒有效截面处的应力593.1MPa≤[σ]。

2.3 螺纹旋合圈数

（1）挤压强度校核：在钢拉杆轴向力作用下，杆体螺纹与调节套筒螺纹受到挤压。将一圈螺纹沿螺纹底径展开，螺纹可视为宽度为πD的悬臂梁[7]，具体如图4 所示。螺纹中径：

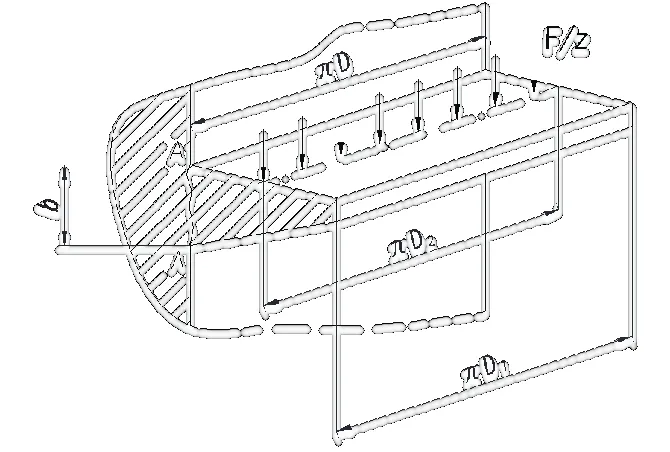
图4 螺纹展开图

普通螺纹工作高度：

根据螺纹的许用挤压应力得到螺纹旋合圈数为：

（2）抗剪强度校核：螺纹悬臂梁的危险截面位于A—A 处，螺纹根部宽度：

根据螺纹的剪切应力得到螺纹的旋合圈数为：

（3）抗弯强度校核：螺纹悬臂梁的抗弯危险截面位于A—A 处，根据螺纹的弯曲应力得到螺纹的旋合圈数为：

综合以上计算结果，得到螺纹旋合圈数应取大值，其中P为螺纹螺距，D为螺纹大径，D1为螺纹小径，[ ]为许用正应力，[τ]为许用剪应力，F为设计承载力。将具体数值代入可得螺纹牙不发生剪切破坏时的最少旋合扣数为18，不发生弯曲破坏时的最少旋合数为19。由调节套筒组装图3，钢拉杆旋合长度为180mm，螺距P=6mm，实际旋合圈数30 圈，满足要求[8-9]。

2.4 支撑套筒应力验算

支撑套筒外径250mm，最大内径190m，内螺纹规格为M195×8。支撑套筒的有效面积大于调节套筒的有效面积，故此处不再对其进行理论计算。

3 有限元分析

考虑ABAQUS 的接触问题分析功能和非线性功能卓越。本文采用大型通用有限元分析软件ABAQUS 对钢拉杆端部节点按实际1：1 足尺建立有限元模型进行分析计算。杆体组装完毕后，均速加载至6 000kN，力-位置曲线处于比例弹性阶段，测得弹性模量为2.33×105Mpa。

3.1 材料本构关系

钢拉杆、调节套筒、支撑套筒的本构关系取为二折线模型，为理想弹塑性。其中弹性模量根据钢拉杆的拉伸试验结果，取为2.33×105N/mm2，如图5 所示。泊松比为0.30，密度取为7 850kg/m3，材料的屈服强度取为835Mpa。

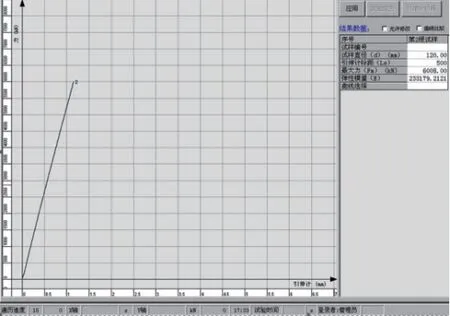
图5 钢拉杆弹性模量试验结果

3.2 有限元模型

有限元建模时，仅将上部钢拉杆、调节套筒、支撑套筒建入模型中，并将下部钢拉杆略去以减少接触的数量，计算分析时以力的作用直接作用于调节套筒的内螺纹处。螺纹的计算分析通常采用做出螺纹实体后采用接触分析，虽然得出的结果精确，但建模工作量大、接触收敛困难。代替实体螺纹建模的操作为：在ABAQUS 接触定义中设置跟螺纹形状相关参数，如螺距、螺纹小径等，摩擦系数取值为0.2，以此模拟真实的螺纹接触情况，既节省了建模时间，又可以得到足够精确的分析结果。具体有限元模型如图6-9 所示。

图6 钢拉杆

图8 支撑套筒

图9 组装模型

计算时，在上部高强度钢拉杆端部施加完全固接约束，为精确模拟钢拉杆端部节点的受力状况，考虑顶层楼面荷载通过支撑套筒上表面，其余荷载通过调节套筒作用于其内螺纹，其中支撑套筒上表面所受荷载为1 000kN，下端钢拉杆轴力为7 500kN，转化为相应的支撑套筒上表面荷载以及调节套筒内螺纹面荷载分别为15.7N/mm2、82.1N/mm2。边界以及荷载分布具体如图10 所示。

图10 荷载布置

网格单元类型选取六面体一阶单元C3D8I，网格尺寸不得大于最小板件厚度的1/2，并在主要应力集中部位进行网格细化，模型有限元模型共有节点36 800 个，单元29 236 个，以提高分析精度。具体网格划分如图11 所示。计算屈服准则采用Von Mises 屈服准则。

图11 网格划分

3.3 计算结果

由计算结果可知，该钢拉杆节点最大位移出现在调节套筒的最下端，大小为1.53mm，调节套筒的最大位移1.35mm，调节套筒的内外螺纹的最大相对滑移量差为0.18mm，其中第一圈滑移距离最大，以后各圈依次降低，具体位移图如图12所示。

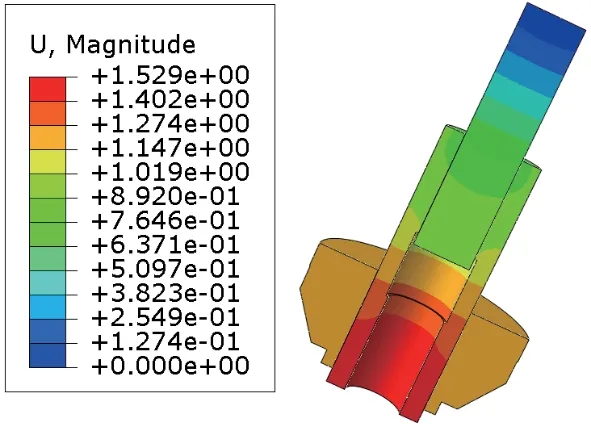
图12 位移图

整体节点的最大应力出现在钢拉杆的丝牙未旋入调节套筒处即上文所述的有效截面处，大小为661.1Mpa；支撑套筒以及调节套筒处的应力最大值出现在调节套筒变阶处，其主要原因为套筒突然变阶导致的应力集中，大小为444.5Mpa；套筒螺纹的最大应力出现在端部旋合第一圈螺纹处，大小约为333Mpa，具体应力分布如图13 所示。

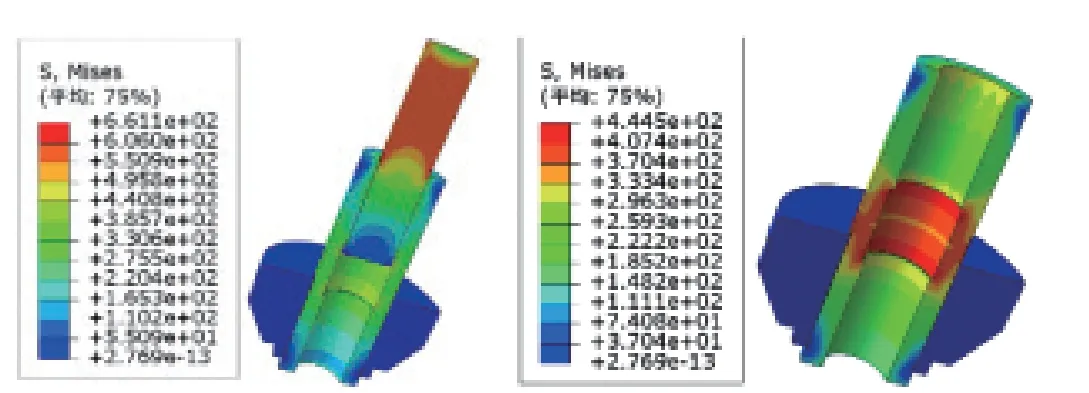
图13 应力图

由《铸钢节点应用技术规程》[10]：

其中σ1、σ2、σ3为计算点第一、第二、第三主应力，σzs为折算应力，βf为折算应力的强度值增大系数，γRE为承载力抗震调整系数。将具体数值代入，可得节点最大应力处：σzs≤βf·f/γRE=918.5MPa，强度满足设计按要求。

4 钢拉杆试验

4.1 试验方案

钢拉杆拉伸实验采用4 000t 卧式拉力试验机，其总长为7m，内部空间为3.5m。为保证试验阶段钢拉杆各组件、试验机受力安全，试验最大拉力荷载定为杆体（未削弱部分）的屈服设计荷载值9 439kN。调节套筒与支撑套筒固定于左侧挡板处，中间采用调节套筒连接两根高强度钢拉杆，右侧通过支撑螺母锁紧于油缸侧挡板，通过操作油压操作台使油缸对右侧挡板产生推力，从而达到对实验对象的拉伸目的，油缸与主结构之间上装有相应的压力传感器，拉力显示表上的数值即是试验中的实际拉力。具体实验组装示意参见图14。

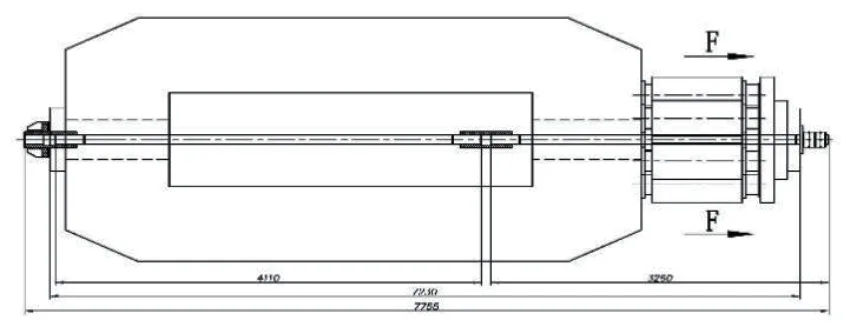
图14 组装图

4.2 试验过程

（1）将拉杆组件与实验工装组装完毕后放入实验机，并调整至相应位置。

（2）安装约束板，并将支撑筒一端固定在试验机约束板外侧，另一端螺杆用螺母锁紧。

（3）开启实验设备，油缸顶升挡板，以不大于10Mpa/s 的速度加载，加载至10%的屈服荷载，消除配合间隙后，记录“初始长度”。

（4）然后继续以不大于10Mpa/s 的速度加载，每加载至预设目标值，记录“实际拉力值”“实际长度”并计算出位移。（5）根据以上记录，绘制相应的拉伸曲线。

4.3 试验结果

4.3.1 钢拉杆承载力验证

试验过程中均速加载至9 439kN，钢拉杆整体组装件（含钢拉杆、中部调节套筒、左侧调节套筒、左侧支撑套筒、右侧支撑螺母）均未出现明显的塑性变形及螺纹破坏，钢拉杆杆体也未出现明显的颈缩。测得的钢拉杆力-位移曲线显示亦未出现明显的屈服台阶，具体结果如图15 所示。

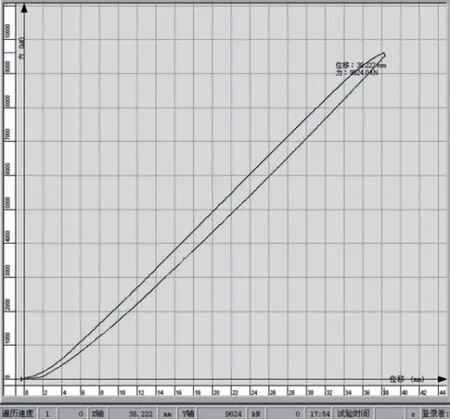
图15 力-位移曲线

各组件测量未发现明显变形，螺纹部位旋合正常，如图16、17 所示。

图16 各组件试验结果

图17 钢拉杆试验结果

4.3.2 钢拉杆弹性模量验证

因各组件之间的螺纹配合必然存在着连接间隙，弹模计算时应将相关螺纹间隙消除，由试验结果可知：当拉伸力小于500kN 时，力-位移曲线呈现明显的非线性关系，故根据力-位移曲线选定弹性直线段时，只需选定直线段起点拉伸力需大于等于500kN 即可保证结果的可靠性。然后在直线段上取相距尽量远的两点之间的轴向力值增量和横向对应的位移增量，再计算弹性模量。本次试验中取弹性直线段的8 个记录点，见表1。分四组根据公式得到弹性模量：E=(ΔF/S)/ (ΔL/L)，其中ΔF为力的增值，S为试样截面，ΔL为位移增量，L为试验杆体长度，计算所得的具体结果，见表2。

表1 记录结果

表2 弹性模量计算结果

由试验结果可知，成品试验弹性模量较单根钢拉杆测得的弹性模量具有一定的离散性，其均值的偏差约为14.2%，但张拉力越大越接近单根钢拉杆的弹性模量。其原因可能为：成品试验弹性模量试验包含杆体、连接套筒、支承套筒、圆螺母、垫板等配件，上述配件通过四组螺纹副组合而成，每个配件的变形都对位移量有影响。

4.3.3 拉杆残余变形及套筒变形

钢拉杆各组件在匀速荷载作用下，加载至最大载荷9 439kN，而后匀速卸载直到试验荷载归零，测得钢拉杆残余变形量为1.3mm 且未发现套筒结构尺寸有明显变化，具体结果如图18 所示。

图18 残余变形图

5 结论

（1）结合设计内力，采用理论公式计算分析得到：钢拉杆端部非镦粗部位的有效截面处应力大小满足材料设计强度指标；钢拉杆杆体螺纹规格为M118X6，调节套筒外径螺纹规格为M195X8，且螺纹旋合圈数不小于19 圈时，螺纹挤压、抗剪、抗弯均能满足设计强度。

（2）对钢拉杆、调节套筒、支撑套筒组成的节点进行有限元计算分析，计算结果显示节点螺纹处应力状态处于弹性阶段，应力分布符合材料性质、加载方式等有关因素，节点变形及各螺纹牙的相对滑移均满足设计要求。

（3）钢拉杆整体组装件在杆体屈服设计荷载值作用下，测得的力-位移曲线未出现屈服台阶，且各配件均未出现明显的塑性变形及螺纹破坏，组装件的残余变形也仅为1.3mm。

以上计算结果与试验相互佐证对工程设计、施工具有实际指导意义。