结构不良问题引入高中数学课堂教学的价值与途径

王锦秋 陈小红 韦煜

［摘  要］ 阐释结构不良问题的理论基础，从发展高阶思维、促进深度学习、培养核心素养及提高问题解决能力等方面分析结构不良问题引入高中数学课堂的价值. 提出结构不良问题融入数学课堂教学的三个途径：基于结构不良问题，开展探究学习；改编结构良好问题，开展习题教学；以结构不良问题为核心，开展专题复习.

［关键词］ 结构不良问题；高中数学；课堂教学

引言

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课程标准》）强调数学与生活以及其他学科的联系，提升学生应用数学解决实际问题的能力［1］. 2020年，教育部考试中心研制的《中国高考评价体系》出版发行. 近年来，基于《课程标准》与《中国高考评价体系》，高考出现了多选题、结构不良问题等创新题型. 结构不良问题由于其独特的结构特点引起了大量一线数学教师的关注，但目前有些一线数学教师对结构不良问题的认识还停留在表层，没有正确认识到结构不良问题的核心价值所在. 这些一线数学教师认为，结构不良问题仅仅是一种新的题型，只是将知识点集成到一个题目中，提供了多种解题途径而已；对结构不良问题的处理方式也限于通过训练让学生适应这种题型，没有深入分析结构不良问题的教育价值和教学功能. 因此，分析结构不良问题引入高中数学课堂教学的价值和途径是很有必要的.

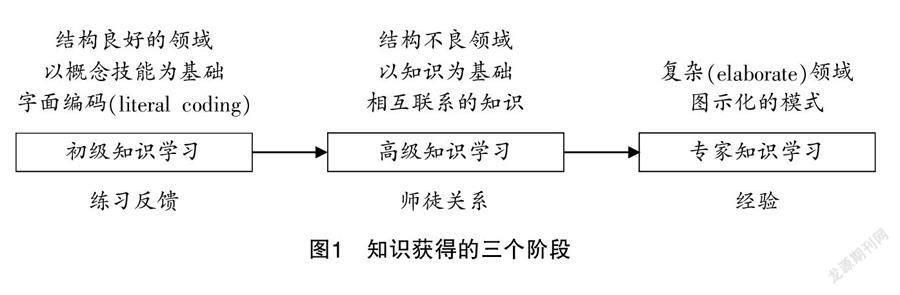
认知心理学家将问题划分为结构良好问题和结构不良问题［2］. 结构不良问题的特点是，其具有多种解决方法、解决途径和少量确定性条件. 这些条件不易操作，且包括某些不确定性因素［3］. 针对复杂和结构不良领域中学习的本质问题，斯皮罗等人提出了认知弹性理论. 认知弹性，即以多种方式重建自己的知识，以便适应复杂多变的情境领域［4］. 斯皮罗等人将学习分为初级学习与高级学习. 初级学习主要涉及结构良好领域，高级学习则主要涉及结构不良领域. 高级学习需要学生把握概念的复杂性，并在具体情境中灵活运用［5］，乔纳森在此基础上提出了知识获得的三个阶段（如图1所示）.

结构不良问题引入高中数学课堂的价值

1.解决结构不良问题是发展学生高阶思维的重要方式

高阶思维是发生在较高认知水平层次上的心智活动或较高层次的认知能力，如分析、综合、评价等［6］，主要解决的是结构不良问题，反映了学习者的问题求解能力、决策能力、批判性思维和创造性思维能力［7］. 结构不良问题往往涉及诸多知识背景及数量关系，学生在自主分析问题的条件、结论以及条件与结论之间的关系的过程中，必然会调动思维，展开联想，建构问题空间. 学生需要分析问题所给的信息，结合自身的已有认知经验筛选合适的条件. 例如遇到条件不足、结论确定的结构不良问题时，学生需要思考补足什么条件才能解决该问题，此时“执果索因”就显得较为有效，同时学生还需要思考“索什么因”；遇到具有多种解决路径的结构不良问题时，学生需要比较各条解决路径间的便捷性、有效性，有助于发展学生的批判性思维；遇到结论开放的结构不良问题时，此时问题的结论（答案）多样化，学生需要结合自身情况发散思维，建构合理、便捷的问题答案. 解决结构不良问题可以促使学生参与思考、分析、评价等思维活动，学生的高阶思维自然能得到发展. 因此，解决结构不良问题是发展学生高阶思维的重要方式.

2.结构不良问题是促进学生深度学习的有效载体

深度学习是一种基于高阶思维发展的理解性学习［8］. 解决复杂现实问题是深度学习的价值所在［9］. 一般来说，复杂现实的问题大多是结构不良问题. 解决这些问题不仅需要掌握相应的知识，更需要掌握方法、原理的切适性，能批判地、正确地分析问题的结构要素间的逻辑关系. 结构不良问题的特点使得学生在解决结构不良问题的过程中需要综合知识，在实际的问题情境中掌握问题的本质，找准问题的关键点，运用恰当的规律和法则，使用合适的策略、方法. 这个过程能有效促进学生批判地思考问题及建构知识网络，实现深度学习. 因此，结构不良问题是促进学生深度学习的有效载体.

3.结构不良问题是培养学生数学核心素养的重要抓手

“问题是数学的心脏”，进行“数学问题解决”是学生发展数学核心素养的有效途径. 对于结构良好问题，学生只需要结合自己已有知识和经验做出抉择，采取特定的解题步骤，就可以得到确切答案［10］. 但解决问题不仅是学生对所学知识与规则的简单应用，而且是学生对自我认知经验与问题情境的有机组合，是在解决过程中建立新规则，发现新原理，获得新策略的过程［11］. 结构不良问题具有解决方案多样、结构开放、巩固知识与培养能力的特点. 结构不良问题的解决过程具备一定的不确定性和挑战性，这与学生对数学的固有认知相矛盾——在学生认知中，数学问题具有唯一确定的答案、明晰的问题条件，解决方法单一，结构不良问题给学生提供了一个认知相矛盾的平台. 这样的矛盾能有效激发学生的求知欲，帮助学生深入理解问题的本质，使学生知道数学也具有不确定性. 从矛盾到再认识、统一的过程中，可以更好地发展学生的数学核心素养. 因此，结构不良问题是培养学生数学核心素养的重要抓手.

4.解决结构不良问题是培养学生问题解决能力的重要途径

问题解决能力是衡量个体智慧和能力高低的指标之一. 目前，在高中数学教育中，学生面对的问题仍然以结构良好问题为主，开放性问题与结构不良问题很少. 较于结构良好问题，结构不良问题在问题结构、问题背景方面更加复杂，解决途径更加多样. 在以往的教学过程中，学生所进行的问题解决活动大多是针对结构良好问题而开展的，主要是对问题解决的关注，對问题发现和问题提出的关注不足. 结构不良问题灵活的结构，利于学生多角度思考，发现问题的关键点，使学生参与到问题的建构过程中，增加学生对数学的体验以及对问题的认识. 通过结构不良问题的解决，可以提高学生问题解决能力. 因此，解决结构不良问题是培养学生的问题解决能力的重要途径.

结构不良问题引入高中数学课堂的途径

1. 基于结构不良问题，开展数学探究学习

有效的数学学习，是学生在教师有效的启发指引下进行自主建构的数学探究学习［12］. 问题是数学探究学习的重要载体，数学探究的结论可以是封闭或者开放的，但数学探究的过程一定是开放的. 数学探究是基于问题的探究，是在教师的引导下学生的自主探究，而不是学生胡乱无目的的探究. 学生要在教师的指导下开展探究活动，获取数学知识、数学方法，发展数学思维. 数学探究学习的学习材料源于书本以及学生学习、生活和参加社会活动的经验. 探究方法基于学生个体的已有认知经验，学生可以根据具体的问题情境、自身的知识储备和认知经验个性化进行探究学习. 结构不良问题具备可调节的开放性，多种解决途径以及结论（答案），是进行探究学习的优良载体，能较好地承载探究学习所需要的条件. 学生进行探究学习时，可根据具体情境，采取合适的方法获取信息，分析问题，灵活选择合适的路径解决问题.

例如，在“基本不等式”的教学中，由a2+b2≥2ab推导出≥（a>0，b>0）（基本不等式）后，教师可以组织学生开展基本不等式的证明活动，让学生自主选择不同方法（如作差比较法、分析法、综合法、几何法等）完成基本不等式的证明，让学生自主建构基本不等式的知识图式. 同时，教师可以将数学史、数学文化融入教学过程，介绍国内外有关基本不等式的证明方法和相关历史，提升学生的数学学习兴趣.

2. 改编结构良好问题，开展习题教学

习题课是教师根据教学要求和学生需要，在课堂上进行范例研究、变式训练，巩固学生所学，训练数学思维，培养解题策略的课型［13］. 因此，习题课是高中数学课程教学中的重要课型. 以往传统的习题课所使用的都是结构良好问题，条件不多不少，解决方法单一，主要功能是巩固知识. 但结构不良问题不仅兼顾结构良好问题的知识巩固功能，还具有可调节的开放性，可以更加有效地调动学生的积极性与数学学习兴趣. 此外，结构良好问题与结构不良问题可以相互转化，可以根据学生实际作答情况进行调整. 在数学教学中，引入结构不良问题，是对传统习题教学的升级再造. 教师可以针对问题结构进行改编，使问题结构变得“模糊”，将结构良好问题转化成结构不良问题.

例如（人教A版普通高中教科书数学必修第一册的第二章第三节习题第5题），已知集合A=｛xx2－16<0｝，B=｛xx2－4x+3>0｝，求A∪B.

这是一道典型的结构良好问题，学生可先改变集合A与集合B的表达形式，再求两集合的并集即可. 教师在此可通过调整问题的条件或结论将该问题转化成结构不良问题，一是更改问题的条件：可以考虑更改集合A，B的表达形式或加入新的集合；二是更改问题的结论：可以构造多个结论任学生自行挑选并求解.

变式1：已知集合A=｛xx2－16<0｝，B=｛xx2－4x+3>0｝，C=｛xx2－x－2<0｝，在集合A，B，C中任选两个，求这两个集合的并集.

变式2：已知集合A=｛xx2－16<0｝，B=｛xx2－4x+3>0｝，U为全集，在结论①A∪B，②A∩B，③A∪CUB，④A∩CUB，⑤CUA∪B中任选三个求解.

3. 开展以结构不良问题为核心的专题复习课

复习课是为了梳理、巩固已学知识和方法，促进知识系统化，提高学生运用所学知识解决问题能力的一种课型［14］. 从结构不良的视角設计复习课，有助于学生从多角度、多层次认识数学知识，有助于增强学生“四基”，培养学生“四能”，促进学生数学素养的发展. 在专题复习课中引入结构不良问题，是传统数学复习课的转型进阶. 教师可以在教学活动的组织方面提出结构不良问题，让学生多角度思考，寻找知识点间的联系，还可以在练习巩固阶段将以往的结构良好问题更改为结构不良问题，有利于建立学生的知识网络.

例如，“空间直线、平面的平行”专题复习课.

【知识梳理】

（1）直线与直线平行的判定定理与性质定理（具体内容略）；

（2）直线与平面平行的判定定理与性质定理（具体内容略）；

（3）平面与平面平行的判定定理与性质定理（具体内容略）.

【知识结构梳理】

“空间直线、平面的平行”专题知识结构如图2所示.

【结构不良问题及练习】

问题1：怎么判定两条空间直线平行？

问题2：怎么判定一条直线与一个平面平行？

问题3：怎么判定两个平面平行？

问题1、问题2、问题3均有多个答案，均为结构不良问题. 问题1可从以下三个角度回答：一是从基本事实出发，即可得到线线平行；二是从线面平行的性质定理出发，可以得到该直线与过该直线的平面和此平面的交线的平行关系；三是从面面平行的性质定理出发，可以得到第三个平面与这两个平面的交线的平行关系. 问题2可从以下四个角度回答：一是从线面平行定义出发得到线面平行的关系；二是由线面平行的判定定理得到线面平行的关系；三是综合线线平行和两平行直线确定一个平面得到线面平行的关系；四是从面面平行的性质出发，也可以得到线面平行的关系. 问题3可从以下三个角度回答：一是面面平行的定义；二是面面平行的判定定理；三是由两组相交直线分别平行即可得到该相交直线所构成的平面平行.

练习1、练习2、练习3分别在问题的解决路径、条件及证明结论中设置了不良结构. 学生可以根据自身的认知经验自主选择不同的解决方案.

练习1：如图3所示，在正方体ABCD-ABCD中，E，F分别为边AD，DD的中点，从“①线线平行”“②线面平行”“③面面平行”中任选一种途径证明EF∥平面BCC.

练习2：如图4所示，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，从①，②，③，④四个正方体中任选一个，判断AB与平面MNP的位置关系并说明理由.

练习3：如图5、图6所示，在三棱柱ABC-ABC中，E，F，G，H，D，D分别是AB，AC，AB，AC，BC，BC的中点，请在①，②两个结论中任选一个进行证明.

①平面EFA∥平面BCHG；②平面ABD∥平面ACD.

【总结归纳】

引导学生总结归纳“空间直线、平面的平行”的知识结构，再次强化学生对本节知识的认识，建立更为清晰的知识网络，将碎片化的知识联系起来.

结语

结构不良问题对发展学生高阶思维、促进学生深度学习、培养学生数学核心素养及提高学生问题解决能力具有重要价值. 教师应将结构不良问题融入数学教学，发挥结构不良问题的教育价值、教学功能，助力学生核心素养的培养与问题解决能力的提高.

参考文献：

［1］ 中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］ Jonassen D H . Toward a Design Theory of Problem Solving［J］. Educational Technology Research and Develo-pment，2000，48（04）：63-85.

［3］ David H. Jonassen，钟志贤，谢榕琴. 基于良构和劣构问题求解的教学设计模式（上）［J］. 电化教育研究，2003（10）：33-39.

［4］ 高文. 认知弹性理论、超文本与随机通达教学——一种折中的建构主义学习与教学理论［J］. 全球教育展望，1998，27（06）：1-4.

［5］ 陈琦，刘儒德. 当代教育心理学［M］. 北京：北京师范大学出版社，2002.

［6］ 钟志贤. 促进学习者高阶思维发展的教学设计假设［J］. 电化教育研究，2004（12）：21-28.

［7］ 赵永生，刘毳，赵春梅. 高阶思维能力与项目式教学［J］. 高等工程教育研究，2019（06）：145-148+179.

［8］ 安富海. 促进深度学习的课堂教学策略研究［J］.课程·教材·教法，2014，34（11）：57-62.

［9］ 马云鹏. 深度学习视域下的课堂变革［J］. 全球教育展望，2018，47（10）：52-63.

［10］馬淑杰，张景斌，陈福印. 数学结构不良问题的育人价值——以高中结构不良数学问题专题复习课为例［J］. 数学通报，2020，59（10）：40-45+52.

［11］武丽莎，朱立明. 高中数学学科核心素养：生成机制与培养路径［J］. 数学教育学报，2021，30（04）：25-29.

［12］曾小平，汪秉彝，吕传汉. 数学“情境—问题”教学对数学探究学习的思考［J］.数学教育学报，2009，18（01）：82-87.

［13］王富英. 论中学数学习题课教学［J］. 数学通报，2020，59（07）：35-39.

［14］顾继玲，章飞. 初中数学单元复习课教学设计的特征分析［J］. 数学通报，2021，60（07）：31-36+41.