基于变形分数阶Lorenz混沌系统的图像加密算法

马英杰 陈椟峣 赵 耿 曾 萍 郭 超

(北京电子科技学院 北京 100070)

0 引 言

图像因其自身的一些固有特性导致部分传统的加密算法不再适用。混沌图像加密可行性好，具有广阔的应用前景。文献[1]使用分数阶Chen超混沌在频域上置乱，再设计超混沌S盒进行代换，最后用双向异或循环左移扩散，从而达到了结合频域与空域，置乱、代换、扩散相统一的加密算法。文献[2]提出了基于混沌系统以及Arnold变换的图像加密算法，密钥采用SHA- 256算法。文献[3]提出基于分数阶Rossler混沌系统的图像加密算法，密钥选取基于混沌系统的阶数以及参数。文献[4]提出基于分数阶Lorenz混沌系统的图像加密算法，置乱后对图像进行扩散，采取基于整数阶和分数阶混沌系统相结合的扩散方法。文献[5]提出基于分数阶混沌系统与DNA编码相结合的彩色图像加密算法，利用分数阶混沌系统和DNA序列加法运算法则，对置乱后的DNA序列矩阵进行加密处理。文献[6]提出了一种基于分数阶Chen超混沌系统和DNA的压缩感知图像加密算法，利用四维分数阶Chen超混沌系统生成测量矩阵，通过全局置乱降低相邻比特之间的相关性，对加扰后的二进制序列和超混沌序列进行DNA操作，提高了算法的效率。文献[7]提出基于分数阶傅里叶变换的双混沌图像加密算法，混沌系统结合傅里叶变换进行明文隐藏，在空域和频域完成置乱。文献[8]提出了一种基于三维Arnold-cat映射和Fisher-Yates洗牌算法的图像加密方案，将一幅平面图像分割成大小相等的多个切片，然后用三维混沌映射对图像进行三维表示，利用分数阶非线性微分方程组实现了混洗图像像素强度值的扩散。文献[9]提出了一个量子三维Baker映射来扰乱图像的三维量子表示，在置换图像上实现广义灰度码，然后使用分数阶Chen混沌系统生成的伪随机序列进行选择位内异或。文献[10]针对Zhao提出的图像加密算法进行分析，仅对一幅图像进行选择明文攻击，就可以很容易地恢复出原始图像和密钥流，数学分析和实验结果都证实了这种攻击的可行性。

本文提出基于变形分数阶Lorenz混沌系统的图像加密算法，密钥生成采用明文图像输入以及SHA- 256算法，基于混沌序列的初始值和Arnold置乱的参数值的确立。加密阶段分为频域上的像素位置置乱和空域上的像素值替代。置乱过程使用非等长的带参数的Arnold置乱，一方面解决了图像长宽比例受限的问题，另一方面也避免了Arnold系统周期性带来的影响。在图像频域上对低频和高频分量分别置乱增强了图像的加密效果。基于混沌序列的扩散方法采用异或运算，置乱图像的像素值以及预处理过的混沌序列相混合从而生成最终的加密图像。

1 分数阶Lorenz混沌系统

1.1 传统分数阶Lorenz混沌系统

分数阶Lorenz混沌系统是目前常用的一种混沌系统，其系统方程如式(1)所示。

(1)

式中：D表示分数阶微分；a、b、c为系统的控制参数；q1、q2、q3为分数阶的阶次。当a=10，b=45，c=8/3时，系统达到混沌态。

1.2 变形分数阶Lorenz混沌系统

本文提出一种基于符号函数的变形分数阶Lorenz混沌系统，其系统方程如式(2)所示。

(2)

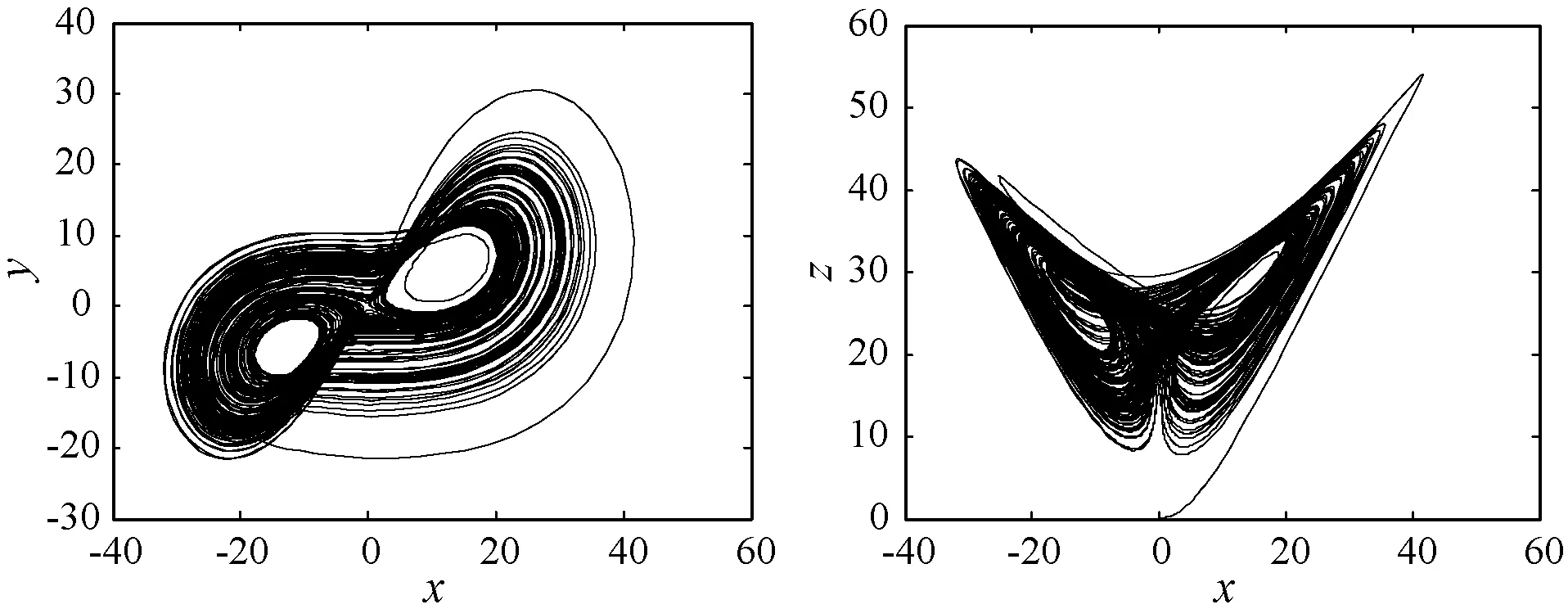
式中：a、b、c、d是系统参数，当a=15、b=0.5、c=27、d=3时，系统达到混沌态。初始值为[0.1,0.1,0.1]，系统的相图如图1所示。其中(a)-(d)分别为x-y、x-z、y-z、x-y-z方向上的相图。

(a) (b)

(c) (d)图1 变形分数阶Lorenz混沌系统相图

2 Arnold置换

2.1 传统Arnold变换

经典的二维Arnold映射如式(3)所示。

(3)

通常经过一次Arnold变换的图像其安全性还不够高，因此一般采用多次置乱方法。然而传统Arnold映射具有周期性特点，本文选择的是有参数的Arnold映射，从而克服其周期性问题，如式(4)所示。

(4)

2.2 非等长Arnold变换

非等长Arnold变换可以针对任意尺寸的图像进行处理，如式(5)所示。

(5)

为了克服Arnold映射的周期性问题，对参数a、b、c、d进行一定条件的约束：

a=1,b>0,c=kN(gcd(M,N))-1,d=1+bc

式中：b、k均可设置为密钥，通过计算获得c、d的值。则以上公式等价于：

(6)

其逆变换公式为：

(7)

3 算法设计

3.1 密钥生成器

本文的密钥生成采用明文图像作为输入，通过SHA- 256算法产生相应的摘要信息。对生成的初始密钥进行分组处理，产生有利于后续不同阶段加密的密钥。因此将256位的密钥流进行分组，每组8位，产生32个分段密钥，如式(8)所示。

K=k1,k2，…，k32

(8)

对密钥流K进行如下处理，通过式(9)产生置乱阶段Arnold映射的参数值b1、k1、b2、k2，通过式(10)产生扩散阶段的混沌系统的初始值x0、y0、z0用于混沌序列的产生，通过式(11)对密钥流的32位信息求和，用于后续混沌序列组合的选择。

b1={(k1⊕k2)+(k2⊕k3)+(k3⊕k4)+(k4⊕k5)}mod 10

b2={(k6⊕k7)+(k7⊕k8)+(k8⊕k9)+(k9⊕k10)}mod 10

k1={(k11⊕k12)+(k12⊕k13)+(k13⊕k14)+(k14⊕k15)}mod 10

k2={(k16⊕k17)+(k17⊕k18)+(k18⊕k19)+(k19⊕k20)}mod 10

(9)

(10)

s=sum(k)

(11)

3.2 加密算法

本文算法首先将明文图像作为输入，通过密钥生成器产生了后续置乱和扩散阶段的密钥。然后将明文图像进行两次离散小波变换，使用不同参数的非等长Arnold映射在频域上分别置乱各分量，像素位置打乱后再进行小波的逆变换，在图像的空域上进行像素值的替换，对图像进一步扩散，从而得到最终的密文图像，图2展示了加密算法的功能流程。

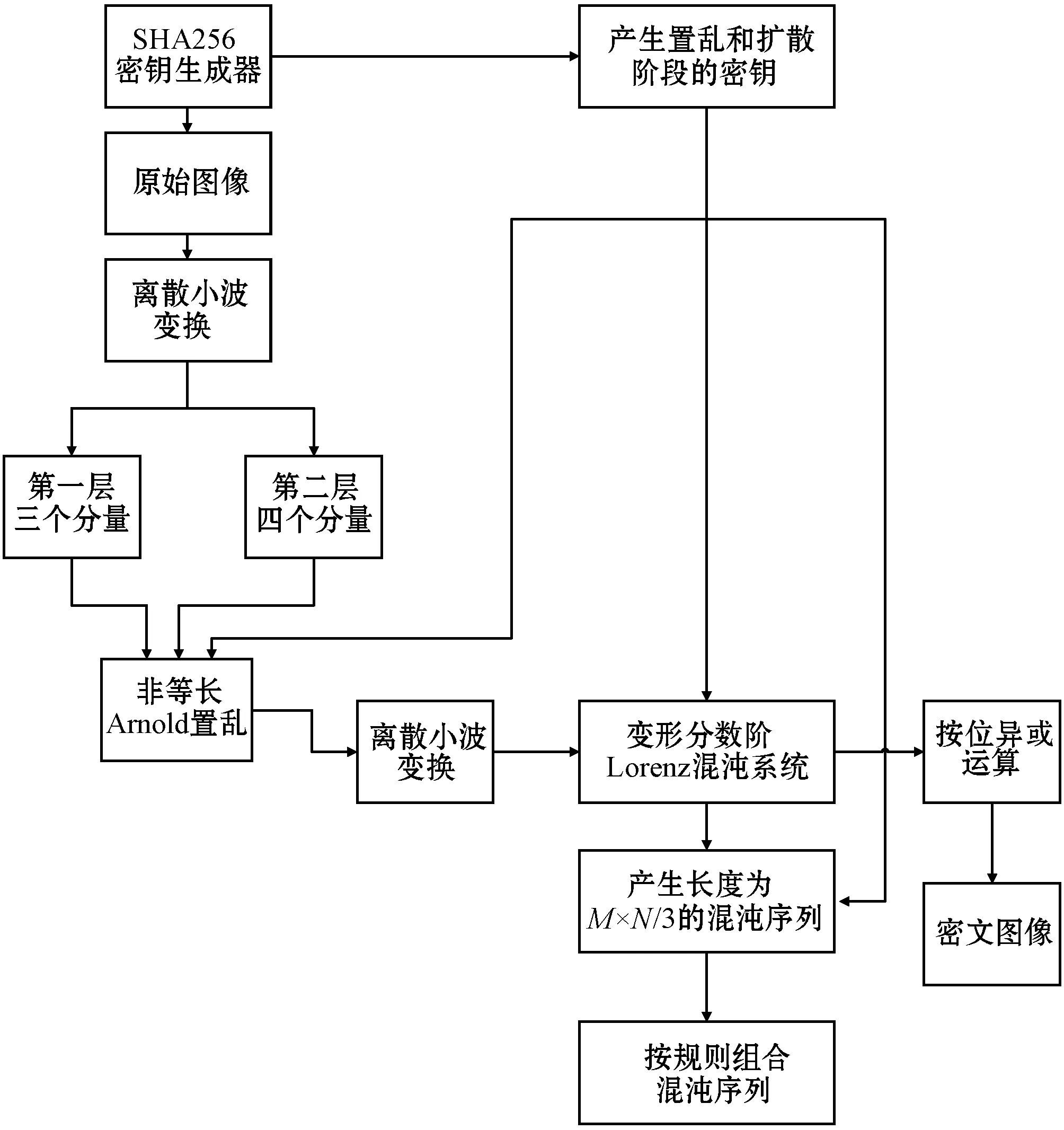
图2 加密算法功能流程

加密算法的步骤如下：

(1) 将M×N的彩色图像进行灰度处理得到原始图像I。

(2) 将图像I作为密钥生成器的输入，基于SHA- 256运算生成64位的摘要值，转化为256位的二进制数，每8位分成一组，得到32位的密钥流K=k1,k2,…,k32。根据式(9)进行运算，产生置乱阶段的密钥，根据式(10)和式(11)计算产生扩散阶段的密钥。

(3) 将原图像I进行两次DWT变换，得到低频分量、水平分量、垂直分量、对角分量，如图3所示。

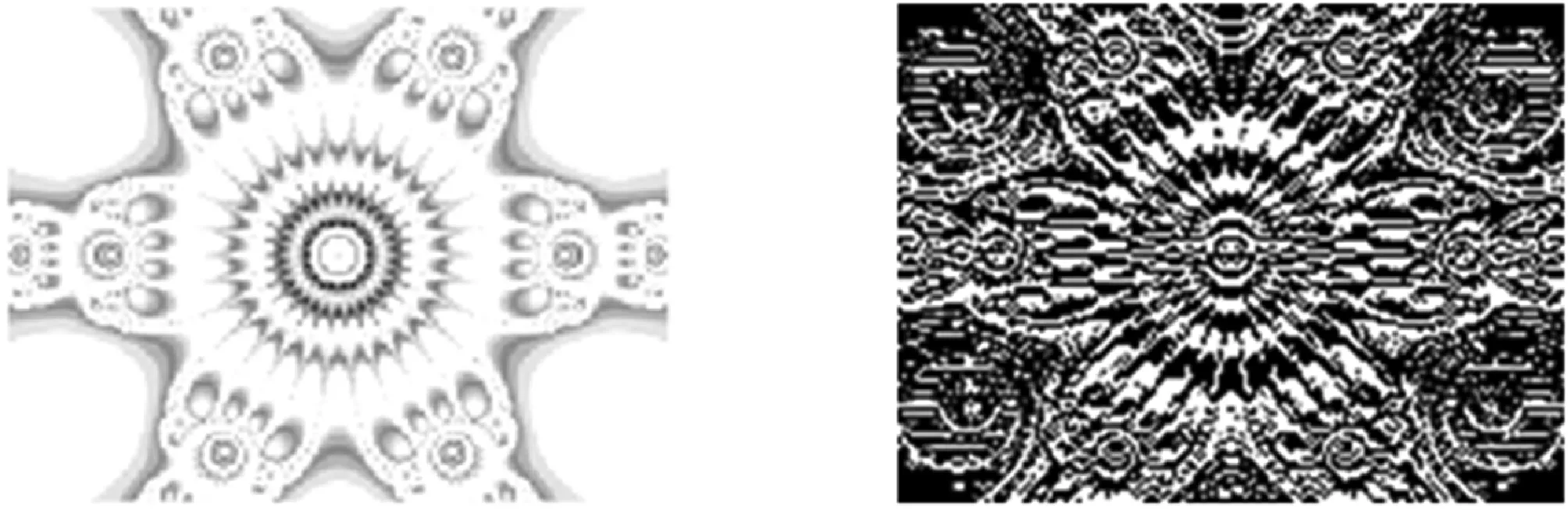
(a) 低频分量 (b) 水平分量

(c) 垂直分量 (d) 对角分量图3 小波变换后得到的四种分量

(4) 将x0、y0、z0作为输入，设置好混沌系统的参数值，取混沌系统的阶次为0.995进行迭代，舍弃前1 000项使产生的加密序列x、y、z达到混沌，最终得到三个长度为M×N/3的加密序列，通过式(12)对x、y、z进行预处理，得到用于扩散阶段的三个混沌序列t1、t2、t3：

t1=mod(1 000×x,256)

t2=mod(1 000×y,256)

t3=mod(1 000×z,256)

(12)

变形分数阶混沌序列的生成及预处理的核心编程如下：

%变形分数阶混沌系统生成混沌序列

parameters=[15,0.5,27,3];

orders=[0.995,0.995,0.995];

Y0=[x0,y0,z0];

[T,Y]=xFOLorenz(parameters,orders,0.005*(ceil(M*N/3)+1 000),Y0);

x=Y(:,1);y=Y(:,2);z=Y(:,3);

%混沌序列预处理

tY=Y(1 001:ceil(M*N/3)+1 000,1:3);

t1=tY(:,1);t2=tY(:,2);t3=tY(:,3);

t1=mod(1 000*t1,256);

t1=uint8(t1);

t2=mod(1 000*t2,256);

t2=uint8(t2);

t3=mod(1 000*t3,256);

t3=uint8(t3);

(5) 使用b1、k1、b2、k2作为非等长Arnold的参数值对图像像素位置置乱。使用b1、k1分别对第一层分解所得三个高频分量进行非等长Arnold置乱，使用b2、k2分别对第二层分解所得四个分量(包含低频分量)进行置乱。设置置乱迭代次数为10。通过式(13)计算得参数c：

c=kN(gcd(M,N))-1

(13)

(6) 置乱后的各分量均做DWT逆变换，产生置乱图像A1。

(7) 扩散阶段混沌序列的选择。不重复组合t1、t2、t3，存在6种情况：[t1,t2,t3]、[t1,t3,t2]、[t2,t1,t3]、[t2,t3,t1]、[t3,t1,t2]、[t3,t2,t1]，将它们从0-5进行有序编号，使用步骤1中获得的s进行如下运算，得到的值，将tk的值作为目标编号，选取对应组合的混沌序列。

tk=mod(s,6)

(14)

像素值替代的核心编程如下：

[m,n]=size(A1);

A1=uint8(round(A1));

tk=mod(s,6);

switch tk

case 0

t=[t1,t2,t3];

case 1

t=[t2,t3,t1];

case 2

t=[t3,t1,t2];

case 3

t=[t1,t3,t2];

case 4

t=[t3,t2,t1];

case 5

t=[t2,t1,t3];

end

(8) 使用以上产生的混沌序列，与置乱图像A1进行按位异或运算，得到最终的加密图像A。

3.3 解密算法

解密过程实质上是加密的逆过程。具体步骤如下：

(1) 利用混沌系统产生混沌序列，进行正确的排列组合形成解密序列，将解密序列与加密图像A进行按位异或运算，得到图像B1。

(2) 将图像B1进行两次DWT变换，产生图像的低频分量、水平分量、垂直分量和对角分量。

(3) 输入非等长Arnold映射的参数值b1、k1、b2、k2，分别对四种分量进行非等长Arnold逆运算，逆变换公式如式(7)所示，设置迭代次数为10。

(4) 将置乱恢复后的各分量进行DWT逆变换，得到最终解密图像B。

4 性能分析

4.1 实验仿真

在MATLAB R2014b平台编程实现提出算法的加密和解密，并进行了性能仿真。实验采用大小为320×240的灰度图像“test”作为原始图像，如图4(a)所示。加密时，改进分数阶Lorenz混沌系统的阶数均设置为0.995，参数a=15、b=0.5、c=27、d=3，初始值为[0.1,0.1,0.1]，Arnold映射的参数b1=0、b2=0、k1=0、k2=0，置乱迭代次数为10，图4(b)展示的是加密图像。可以看到，原始图像与加密图像之间看不出任何联系，具有较好的视觉效果。

(a) 原图 (b) 加密图图4 实验结果

4.2 密钥空间分析

密钥空间由提出的图像加密方案中所有可能的密码密钥组成。理论证明，密钥空间至少应大于2100才具有较高的安全级别[1]。对于本文提出的加密算法，密钥由明文图像的256位二进制摘要值产生，因此能提供的密钥空间为2256，远远大于应该满足的最小值。因此，本文算法具有能够有效抵御暴力攻击的能力。

4.3 直方图分析

直方图通过绘制每个灰度级别的像素数来显示图像中不同像素值的分布。对明文图像使用本文算法进行加密，加密前和加密后图像的直方图如图5所示。

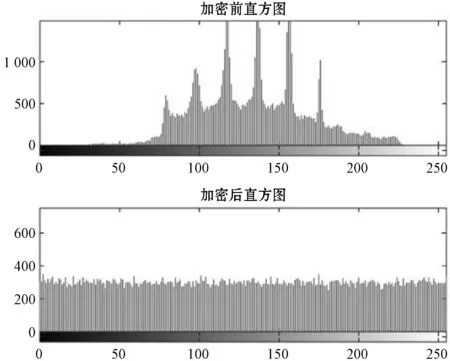
图5 明文图像和密文图像的直方图

4.4 相关性分析

为了比较明文图像和密文图像中相邻像素的相关性，分别抽取了5 000对像素，计算所选对的水平、垂直和对角方向上的相邻像素的相关系数，如表1所示。

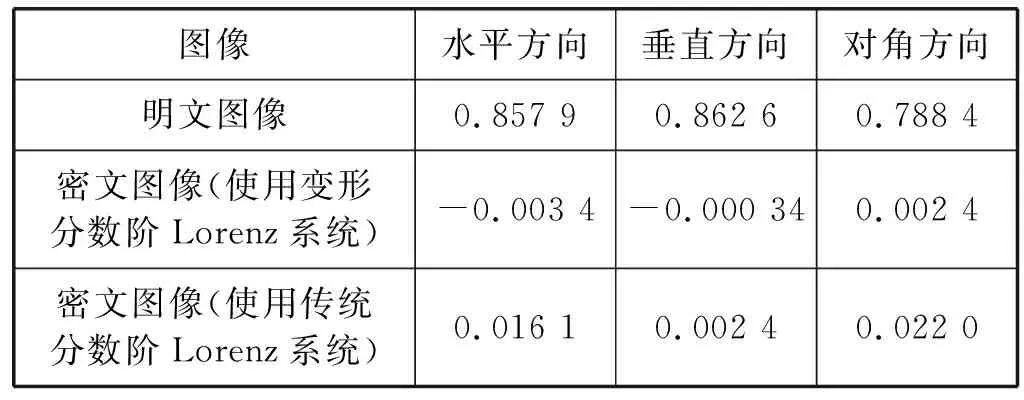
表1 明文图像和密文图像相邻像素相关性比较

可以看出，使用改进分数阶Lorenz混沌系统加密所得出的相关性系数比使用传统分数阶Lorenz混沌系统的更接近于0。

4.5 差分攻击分析

对于有效的加密方案，明文图像的细微差异都将导致密文图像的巨大变化。在差分攻击阶段，采用NPCR和UACI两个指标用于分析抵御选择明文攻击能力。NPCR和UACI的计算公式如下：

(15)

(16)

(17)

式中：W、H是图像的宽度和高度；C1、C2为两幅待比较的密文图像。理想状态下，RNPC=99.609%，IUAC=33.463%。首先使用本文的加密方案对原始明文图像进行加密，并获得一个标准的密文图像C1。然后将随机抽取明文图像的一个像素值加1处理得到一个新的明文图像，不改变加密系统的任何参数值进行加密得到新的密文图像C2。最后将新的密文图像C2与原有的密文图像C1进行比较，计算它们的NPCR和UACI值。重复以上操作四次，抽取四对像素值计算结果，结果如表2所示，在表3中将本文的仿真结果与其他几篇文献进行了比较。

表2 加密图像间不同像素点的NPCR和UACI(%)

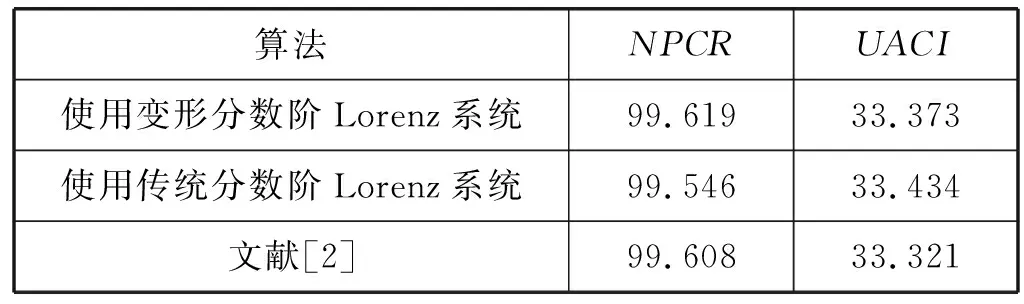
表3 不同算法的NPCR和UACI比较(%)

5 结 语

本文提出一种基于变形分数阶Lorenz混沌系统的图像加密算法，设计一个密钥生成器，采用Hash算法将密钥与明文图像的摘要值紧密地关联起来，优化了算法抵御选择明文攻击的能力。在置乱阶段，对明文进行离散小波变换，将高频与低频分量的图像使用不同的参数分别置乱。本文引入了非等长的带参数的Arnold映射，一方面解除了加密对明文图像的尺寸要求，另一方面避免了传统Arnold映射的周期性影响导致的加密不成功。仿真结果表明，本文算法密钥空间大、密钥敏感性高、密文统计直方图分布均匀、相邻像素相关性低、信息熵接近于理想值、抗差分攻击能力强，具有较高的安全性。