新型组合波形钢腹板的弹性剪切屈曲强度

郑尚敏, 沈 强, 程海根,2, 唐维胜, 管 冲

(1.华东交通大学 土木建筑学院, 江西 南昌 330013;2.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室, 江西 南昌 330013)

0 引言

波形钢腹板因其较好的平面外刚度和较高的剪切屈曲强度，被广泛应用于大跨度屋顶、钢板剪力墙和桥梁等结构的工程应用中。波形钢腹板组合箱梁桥主要由混凝土顶底板、波形钢腹板和预应力筋组成。波形钢腹板取代混凝土腹板，具有有效降低桥梁上部结构自重和减少预应力损失等诸多优点[1-2]。该类型桥梁中，波形钢腹板主要承担截面的剪力，不承担截面的弯矩[3-4]，因此桥梁的极限承载力与波形钢腹板的剪切屈曲强度密切相关。

近年来，大量学者对波形钢腹板的剪切屈曲行为开展了大量研究，Easley等[5]于1969年掀起对波形钢腹板梁剪切屈曲试验研究的序幕；随后Elgaaly，Moon等[6-7]多位学者进行了相关试验和数值模拟，指出初始缺陷对波形钢腹板抗剪性能有一定影响，并提出了局部屈曲、整体屈曲和组合屈曲计算公式；聂建国、朱力等[8-9]对4种边界波形钢腹板的剪切屈曲强度公式进行了推导，并通过大量数值研究，提出了能够同时考虑3种屈曲模式的弹性剪切屈曲强度计算公式；李立峰等[10]通过4根波形钢腹板钢梁剪切屈曲试验，对弹性屈曲强度计算公式进行了简化；冀伟等[11]基于薄板小挠度理论和正交异性板理论,对变截面波形钢腹板的剪切屈曲强度计算公式进行了推导；王银辉等[12]通过量化分析指出了现有波形钢腹板弹性局部剪切屈曲强度计算方法的局限性，并提出了一种适用范围更广、精确度较高的计算公式。

综上所述，以上研究主要针对波形钢腹板的剪切屈曲强度公式进行研究，关于提高波形钢腹板抗屈曲能力的研究则较少[13-15]。为此本研究提出组合型波形钢腹板(由不同波纹型号的波形钢腹板组合而成)，采用有限元软件对其进行弹性剪切屈曲分析，并对该组合波形钢腹板的适用性进行研究，以期提高波形钢腹板的抗屈曲能力。

1 计算模型

1.1 组合波形钢腹板的设计

组合波形钢腹板的设计为两种型号的波形钢腹板进行组合，组合时，两种型号波形钢腹板的几何尺寸、形状系数以及折角均不改变。本研究以1600型和1200型波形钢腹板建立的，形成1600～1200型(以下简称1612型)组合波形钢腹板为主要研究对象，如图1所示,对比分析组合波形钢腹板与已有型号波形钢腹板的抗屈曲性能。

图1 1612型组合波形钢腹板(单位:mm)Fig.1 1612 type composite CSW(unit: mm)

1.2 有限元模型

实际工程中，波形钢腹板组合箱梁桥混凝土翼缘刚度较强，对波形钢腹板具有固定约束作用，在波形钢腹板剪切屈曲试验中，H形波形钢腹板梁侧向刚度较小，本研究忽略翼缘和加劲肋等对波形钢腹板剪切性能的影响，将波形钢腹板边界条件简化为更加保守的四边简支[9](见表1)，以重点研究组合波形钢腹板的抗屈曲能力。本研究利用有限元软件ANSYS对波形钢腹板弹性剪切屈曲进行分析，有限元模型及加载方式如图2所示。四边简支和剪切荷载可保证波形钢腹板处于纯剪切受力状态[16-17]。波形钢腹板采用SHELL181进行离散，钢材弹性模量E=206 000 MPa，泊松比v=0.3。对模型进行特征值屈曲分析，以一阶特征值求得弹性剪切屈曲强度。

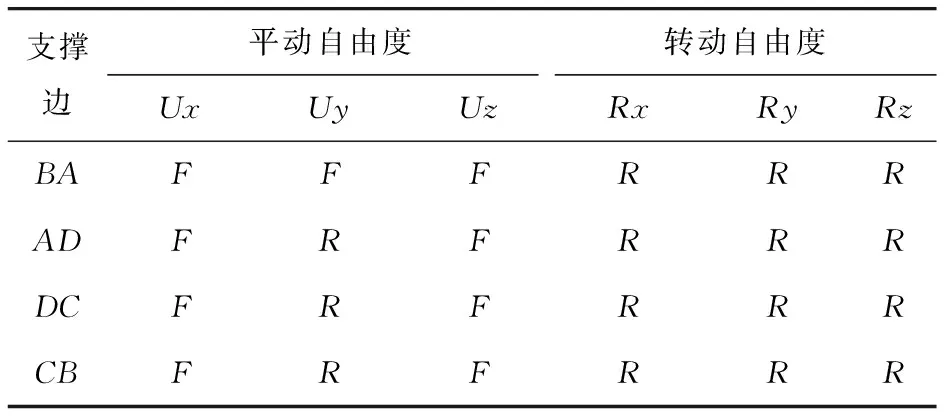
表1 波形钢腹板边界约束Tab.1 Boundary constraint of CSW

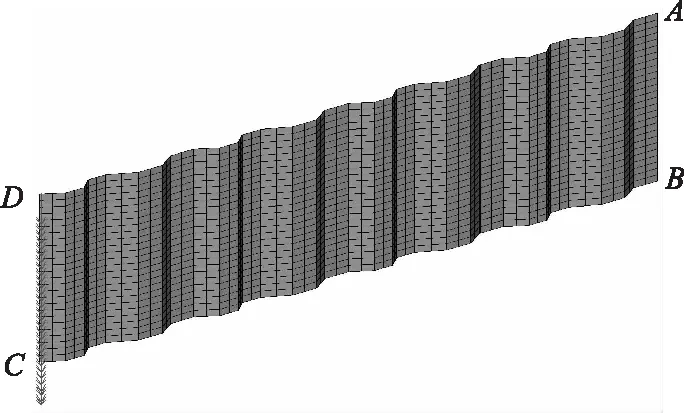
图2 有限元模型Fig.2 Finite element model

1.3 模型验证

为验证本研究建模方法的正确性，对长宽10 m的矩形薄板进行弹性剪切屈曲分析，边界条件和荷载施加方法如1.2节所述。有限元模型中通过变换薄板的长宽比得到不同长宽比下薄板的剪切屈曲系数k。计算解、精确解和常用公式k=5.34+4(b/a)2(b为板高度、a为板长度)结果[18]如图3所示。对比发现，计算解与精确解和公式解吻合较好，表明本研究建模方法能够较好地模拟薄板在剪切荷载作用下的响应。

图3 计算结果对比Fig.3 Comparison of calculation results

2 波形钢腹板剪切屈曲敏感性分析

本节分析了组合波形钢腹板的高厚比和长厚比以及组合类型对波形钢腹板剪切屈曲性能的影响。

2.1 高厚比

为对比分析不同高厚比下1200，1600，1612型组合波形钢腹板的抗屈曲能力，利用有限元分析方法对9个系列、3种不同高度、72个11.2 m长的波形钢腹板有限元模型进行计算分析，得到各模型的剪切屈曲强度，3种型号波形钢腹板的屈曲强度与不同高厚比之间的关系如图4所示。

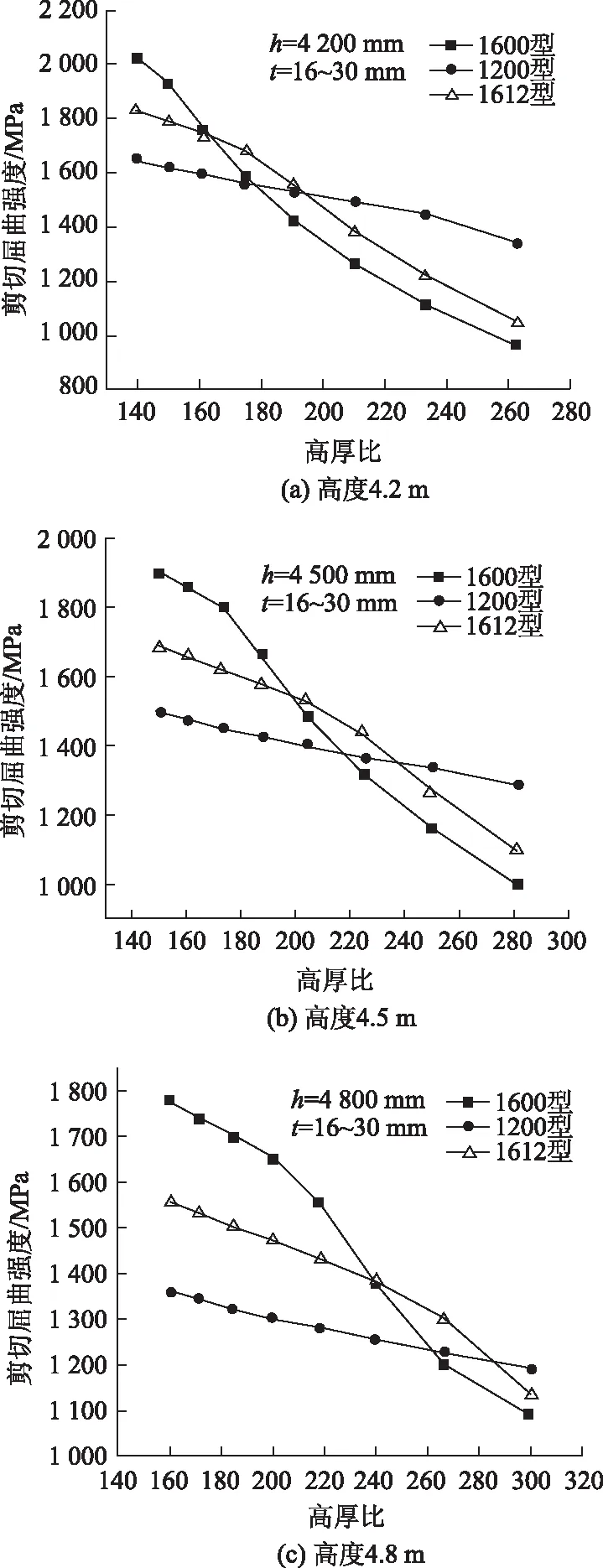
图4 波形钢腹板屈曲强度与高厚比(h/t)的关系Fig.4 Relationship between buckling strength and height-thickness ratio of CSW

由图4可知，不同型号波形钢腹板的屈曲强度与高厚比的关系曲线总体趋势类似，高厚比增大，波形钢腹板屈曲强度减小。不同波纹型号波形钢腹板的剪切屈曲强度大小变化可分为3个阶段。以图4(a)为例，对1612，1600，1200型3种波纹型号波形钢腹板的剪切屈曲强度变化进行分析，第1阶段，腹板厚度小于21 mm(高厚比大于210)时，1200型波形钢腹板的剪切屈曲强度较大；第2阶段，腹板厚度在21～26 mm(高厚比为160～210)时，1612型波形钢腹板的剪切屈曲强度较大，与1600型和1200型相比可提高7.6%；第3阶段，腹板厚度大于26 mm(高厚比小于160)时，1600型波形钢腹板的剪切屈曲强度较大。腹板高度增加，1612型和1200型波形钢腹板较大剪切屈曲强度厚度区间减小，1600型波形钢腹板较大剪切屈曲强度厚度区间增大，如表2所示。

表2 不同型号波形钢腹板较大屈曲强度厚度区间Tab.2 Larger buckling strength thickness ranges of different types of CSW

由以上分析可知，在不同高度下，均存在1612型组合波形钢腹板较大剪切屈曲强度厚度区间，此时，1612型波形钢腹板的屈曲强度较大；组合波形钢腹板的剪切屈曲强度随高厚比的增大而减小；当组合波形钢腹板长度不变时，随着组合波形钢腹板高度的增加，较大剪切屈曲强度的厚度减小；故在实际桥梁设计中需考虑高度对组合波形钢腹板剪切屈曲强度的影响。

2.2 长厚比

对6.4，11.2 m和15.8 m这3种长度不同厚度的波形钢腹板进行特征值屈曲分析，计算得到1600，1200，1612型3种波纹型号与长厚比的波形钢腹板剪切屈曲强度-长厚比关系曲线，如图5所示。

图5 波形钢腹板屈曲强度与长厚比的关系Fig.5 Relationship between buckling strength and length-thickness ratio of CSW

由图5可知，3种波纹型号波形钢腹板的剪切屈曲强度与长厚比曲线与前述中不同高厚比曲线变化趋势类似，可分为3个阶段。以图5(c)为例，第1阶段，腹板厚度小于21 mm(长厚比约750)时， 1200型波形钢腹板的剪切屈曲强度较大；第2阶段，腹板厚度在21～26 mm(长厚比约600～750)时，1612型波形钢腹板的剪切屈曲强度较大，与1600型和1200型的剪切屈曲强度相比可提高7%；第3阶段，腹板厚度大于26 mm(长厚比约600)时，1600型波形钢腹板的剪切屈曲强度较大。腹板长度不同时，3种波纹型号波形钢腹板较大剪切屈曲强度厚度区间如表3所示。

表3 不同型号波形钢腹板较大屈曲强度厚度区间Tab.3 Larger buckling strength thickness ranges of different types of CSW

由以上分析可知，组合波形钢腹板的剪切屈曲强度随长厚比的增大而减小；不同长度下，均存在1612型组合波形钢腹板较大剪切屈曲强度厚度区间，此时，1612型波形钢腹板的屈曲强度较大；当组合波形钢腹板高度不变时，改变组合波形钢腹板长度，对其较大剪切屈曲强度厚度区间的影响较小；结合2.1节可知，组合波形钢腹板设计应优先考虑高度的影响。

2.3 组合类型

本节以国内外常用的1600，1200，1000型波形钢腹板组合形成的1612,1610,1210型组合波形钢腹板为例，选取高度和长度分别为4.2 m和11.2 m、腹板厚度8～30 mm的腹板，得到不同型号的组合波形钢腹板剪切屈曲强度，如图6所示。

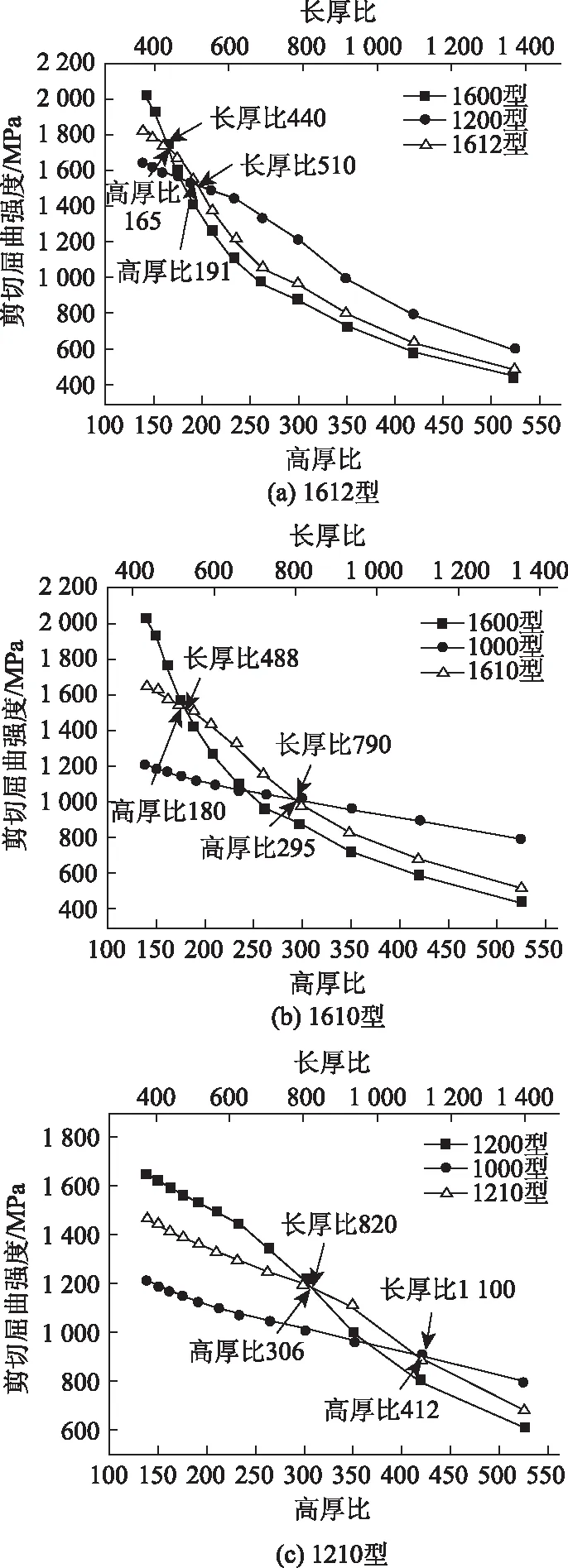
图6 不同组合类型波形钢腹板屈曲强度Fig.6 Buckling strengths of different combination types of CSW

由图6可知，3种型号组合波形钢腹板的剪切屈曲强度变化规律与前述规律类似，在两个非组合波形钢腹板剪切屈曲强度较接近时的厚度区间内，组合波形钢腹板的剪切屈曲强度均较大；当较大型号的组合波形钢腹板转变为小型号时，组合波形钢腹板较大剪切屈曲强度厚度减小，如1612型转变为1210型，1612型组合波形钢腹板较大剪切屈曲强度高厚比区间为165～191，1210型组合波形钢腹板较大剪切屈曲强度高厚比区间为306～412。

由上述可知，组合波形钢腹板的剪切屈曲强度变化规律不受组合波形钢腹板型号的影响，3种型号组合波形钢腹板均存在较大剪切屈曲强度厚度区间，但组合波形钢腹板较大剪切屈曲强度厚度的大小受组合波形钢腹板型号的影响较大。

3 实例对比分析

以某一变截面波形钢腹板钢箱-混凝土组合梁墩顶处的波形钢腹板为研究对象，该节段变截面波形钢腹板长度为3.63 m，墩顶处腹板高度为5.25 m，第1道横隔板处腹板高度为4.24 m，厚度为20 mm，材料与前述所用一致，波形钢腹板采用1600型；等截面波形钢腹板以变截面波形钢腹板为基础进行调整，高度取变截面平均高度4.8 m，其他参数均一致。为分析组合波形钢腹板的抗屈曲性能，仅将等截面和变截面腹板波形更改为1612型和1200型进行对比分析，其他参数均相同。计算得到3种型号不同截面的剪切屈曲强度，如表4所示。

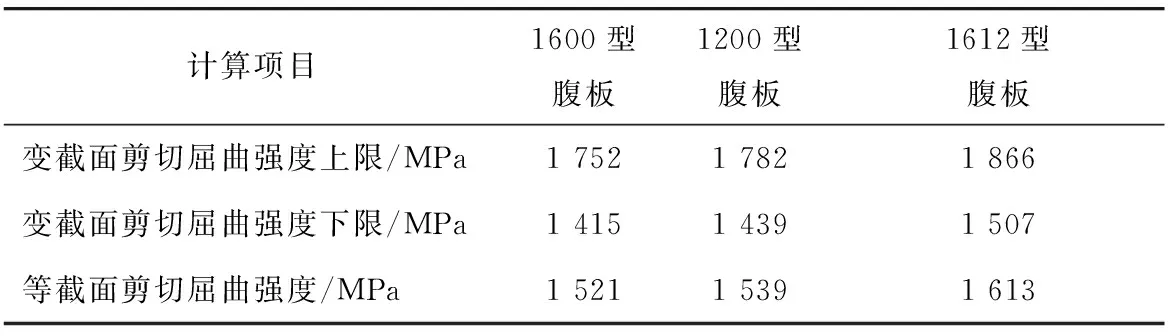
表4 不同型号波形钢腹板屈曲强度Tab.4 Buckling strengths of different types of CSW

由表4可知，3种波纹型号不同截面的波形钢腹板剪切屈曲强度相比，1612型的等截面和变截面波形钢腹板剪切屈曲强度均达到较大值，1612型与1200型和1600型波形钢腹板的剪切屈曲强度相比，变截面波形钢腹板的剪切屈曲强度分别增大了4.7%和6.5%；等截面波形钢腹板的剪切屈曲强度分别增大了4.8%和6%。

通过对上述3种不同波纹型号的变截面和等截面波形钢腹板进行计算分析可知，使用1612型组合波形钢腹板可提高变截面和等截面波形钢腹板的抗屈曲性能。

4 结论

(1)不同高度下，1612型组合波形钢腹板均存在较大剪切屈曲强度厚度区间，1612型组合波形钢腹板的剪切屈曲强度随高厚比的增大而减小；随着腹板高度增加，1612型组合波形钢腹板较大剪切屈曲强度的厚度减小。

(2)不同长度下，1612型组合波形钢腹板均存在较大剪切屈曲强度厚度区间，1612型组合波形钢腹板的剪切屈曲强度随长厚比的增大而减小；改变腹板长度，对组合波形钢腹板较大剪切屈曲强度厚度区间的影响较小。

(3)组合波形钢腹板的剪切屈曲强度变化规律不受组合波形钢腹板型号的影响，不同型号组合波形钢腹板均存在较大剪切屈曲强度厚度区间，当组合波形钢腹板由大型号转变为小型号时，组合波形钢腹板的较大剪切屈曲强度厚度减小。

(4)实际工程对比中，1612型变截面与等截面组合波形钢腹板的剪切屈曲强度均大于1200型和1600型波形钢腹板的剪切屈曲强度，提出的组合波形钢腹板具有一定适用性。