明代虚劳专著及专篇虚劳方药的分布特性研究
卢伟名 罗广波
1(广州中医药大学公共卫生与管理学院 广东 广州 510006) 2(广州中医药大学第一临床医学院 广东 广州 510405)
0 引 言
既往的研究表明,幂律现象在现实世界中广泛存在。近年来,幂律现象受到越来越多不同领域的学者们的关注,逐渐成为物理学、计算机科学、语言学、地球物理、神经科学、社会学、经济学、生命科学及医学等多个学科领域的研究热点。刘冰等[1]发现IPv6 AS级复杂网络中的节点度分布情况满足幂律分布。冼伟成等[2]发现面向对象软件度量因子服从幂律分布。Navas等[3]发现地震震级的频率分布是遵循幂律分布的。Whittles等[4]则发现个体在特定时间段内性伴侣的数目服从幂律分布。孟磊等[5]对工智能、生物和财经3个领域的中文文献的关键词进行了统计,发现关键词的词频分布服从幂律分布。Ma[6]发现人体微生物种群多样性的分布是服从幂律分布。Gardner等[7]发现人体食管pH值的频率分布服从幂律分布。Leskovec等[8]对美国专利引文网络做了统计分析,发现网络节点的度值服从幂律分布。张重阳等[9]发现百度百科词条的编辑时间间隔服从幂律分布。
然而,有学者对幂律分布的普适性提出了质疑。Broido及Clauset[10]的研究发现,目前大部分关于复杂网络的幂律现象的研究缺乏严谨、规范的论证及检验,其结果的可信度较低。同时该学者通过对不同领域的927份网络参数集进行分析,采用一系列严谨、规范的检验方法对其进行幂律分布检验,结果发现仅4%的数据能够确定是服从幂律分布的。基于此,Clauset[10-11]提出了一套基于极大似然估计的结合计算机模拟仿真的幂律分布检验方法,对参数集进行幂律拟合、参数估计及幂律分布检验,是目前较为严谨、规范及可靠的幂律分布的分析及检验方法。
虚劳病指脏腑元气亏损,精血不足为主要病理过程的一类慢性虚衰性病证的总称[12]。关于虚劳病的论述,以明代医家最为详尽、独到[13]。明代虚劳名家辈出,著述颇丰,相关著作的虚劳调治理论及组方用药各具特色,具有极大的研究价值。既往的研究发现,唐诗、宋词、元曲中的汉字及流行歌曲歌词的字频的频率分布皆服从幂律分布[14-15]。因此,本研究推测明代虚劳专著(专篇)中虚劳方剂的中药使用频数的频率分布亦服从幂律分布。另外,本研究通过构建明代虚劳专著(专篇)中虚劳方剂的中药配伍关系网络,研究中药在配伍网络中的度值的频率分布,同时猜测其中药度值的频率分布亦服从幂律分布。此外,本研究采用上述基于极大似然估计的结合计算机模拟仿真的方法对明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布进行幂律分布拟合、参数估计及幂律分布检验。通过研究明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布,并采用严谨、规范的科学方法检验其是否服从幂律分布,可以挖掘明代虚劳方药的用药特色及配伍模式,有利于指导临床用药及实验研究,最终造福于虚劳病患者。
1 数据与方法
1.1 数据来源与规范化
通过在线检索中华医典古籍数据库或查阅纸质版文献,收集整理明代医家辨治虚劳的文献。其中,文献的纳入标准为:
(1) 成书于明代(1368年-1644年);
(2) 虚劳病专著或综合性医著中的虚劳病篇。
文献的排除标准为:
(1) 不涉及虚劳辨治的虚劳病专著或综合性医著中的虚劳病专篇;
(2) 未记载有虚劳方药的虚劳病专著或综合性医著中的虚劳病专篇。
完成文献的筛选后,进一步提取明代虚劳专著(专篇)中的虚劳方药数据,利用Excel 2013储存及管理上述方药数据,进而构建明代虚劳专著(专篇)的虚劳方药数据库,同时以《中华人民共和国药典(2015年版)》[16]《中药大辞典》[17]《本草纲目》[18]及《中药学》[19]为标准和依据,对虚劳方剂中的中药名称进行规范化处理。
1.2 中药配伍关系网络的构建
在中医临床实践中,中药与中药间常配伍使用,组合形成方剂,才可以应用于疾病的治疗中。中药的配伍关系可以看作是一个复杂网络:每一味中药相当于复杂网络中的一个节点,而节点与节点的连边表示中药间的配伍关系。由此构建明代虚劳专著(专篇)的中药配伍关系网络。
1.3 数据的处理与分析
本研究利用Python 3.6.3统计明代虚劳专著(专篇)所记载的虚劳方剂中,各中药的使用频数;利用Pajek 5.08构建中药配伍关系网络,并计算中药配伍关系网络中的各中药的度值。此外,本研究从所有的明代虚劳专著(专篇)中随机抽取5部虚劳专著(专篇),按上述方法分别统计其所载虚劳方剂中,各中药的使用频数及度值。
1.4 幂律分布的拟合与参数估计
采用离散数据的极大似然估计法估计中药使用频数及中药度值频率分布的幂律拟合参数(α),同时采用Kolmogorov-Smirnov(KS)法确定中药使用频数及中药度值参数集中,满足幂律分布的最小变量(xmin)。
应注意,幂律分布与指数分布两者较为相似,皆具有“重尾”特征,因此在对参数集进行幂律拟合时,要注意与指数拟合进行比较。通过绘制观测参数集频率分布在双对数坐标系中的形态可对两种分布进行初步的比较及判断:符合幂律分布的频率分布其形态在双对数坐标系中应近似一条直线,而符合指数分布的频率分布其形态在双对数坐标系中近似一条弧线。另外,也可通过计算r值对两种分布进行的比较及判断。r值的计算公式为:
(1)

(2)
式中:PPL(x)表示幂律分布的概率密度函数;PEXP(x)表示指数分布的概率密度函数。若r>0,表示参数集的频率分布更倾向于服从幂律分布;若r=0,表示参数集的频率分布既不服从幂律分布,也不服从指数分布;若r<0,表示参数集的频率分布倾向于服从指数分布。
在求得r值后,需对r值作进一步的假设检验,其步骤如下:
(1) 提出假设:H0为r=0,H1为r≠0;
(2) 参数估计:计算Q值需先估算r值的均值μ及标准差σ。由于此时已假设r=0,故而其均值μ=0。对于σ,其计算公式为:
(3)
其中:
(4)
(5)
(3) 计算Q值:Q值的计算公式为:
(6)
若Q≤0.10[10-11],则拒绝H0假设,认为r≠0,r可用于比较两种分布拟合程度的优劣。
幂律分布的拟合及参数估计主要通过Python中的powerlaw包[20]实现。
1.5 幂律分布的检验
本研究主要参考了Clauset提供的方法,采用基于极大似然估计的结合计算机模拟仿真的方法进行幂律分布检验,其过程包括:
(1) 对实际参数集的频率分布进行幂律拟合及参数估计,估算幂律参数α及xmin,以及确定x=xmin时,实际参数集的KS统计量(D值)。
(2) 以步骤1中求得的α及xmin进行幂律生成,生成一定数量的拟合参数集,并进一步计算拟合参数集的D值。
(3) 进行假设检验:H0为实际参数集的频率分布与幂律分布没有差异,H1为实际参数集的频率分布与幂律分布有差异。
(4) 计算P值:P值即为拟合参数集的D值大于实际参数集的D值的概率,其计算公式为:
(7)
式中:S表示拟合参数集的总数目;N表示D值大于实际参数集D值的拟合参数集的数目,若P≥0.10[10-11],则不拒绝H0,认为实际参数集的频率分布符合幂律分布。
上述计算皆通过Python中的powerlaw包实现。
1.6 拟合参数集的生成及调整
为使拟合参数集尽可能地接近实际参数集,在生成拟合参数集后,还需对其进行如下调整:
(1) 计算实际参数集的变量个数及其满足x≥xmin的变量个数,分别记为n和ntail。
(2) 生成全幂律参数集:进行幂律参数生成,生成约10 000个满足x≥xmin的变量,形成全幂律参数集。
(3) 生成拟合参数集:拟合参数集的变量个数设置为n,在拟合参数集生成之后,仅保留其满足x≥xmin的变量,其数目记为n0。
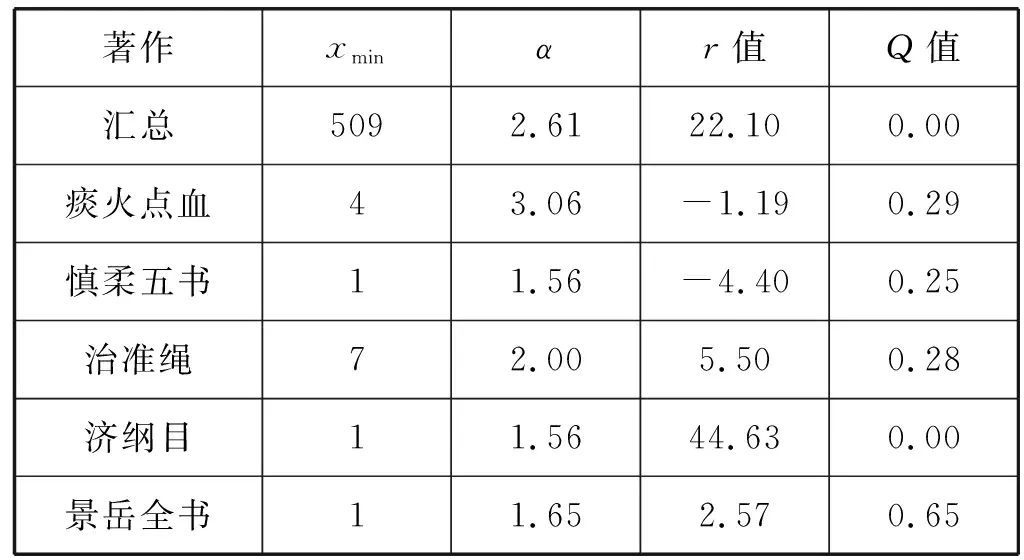
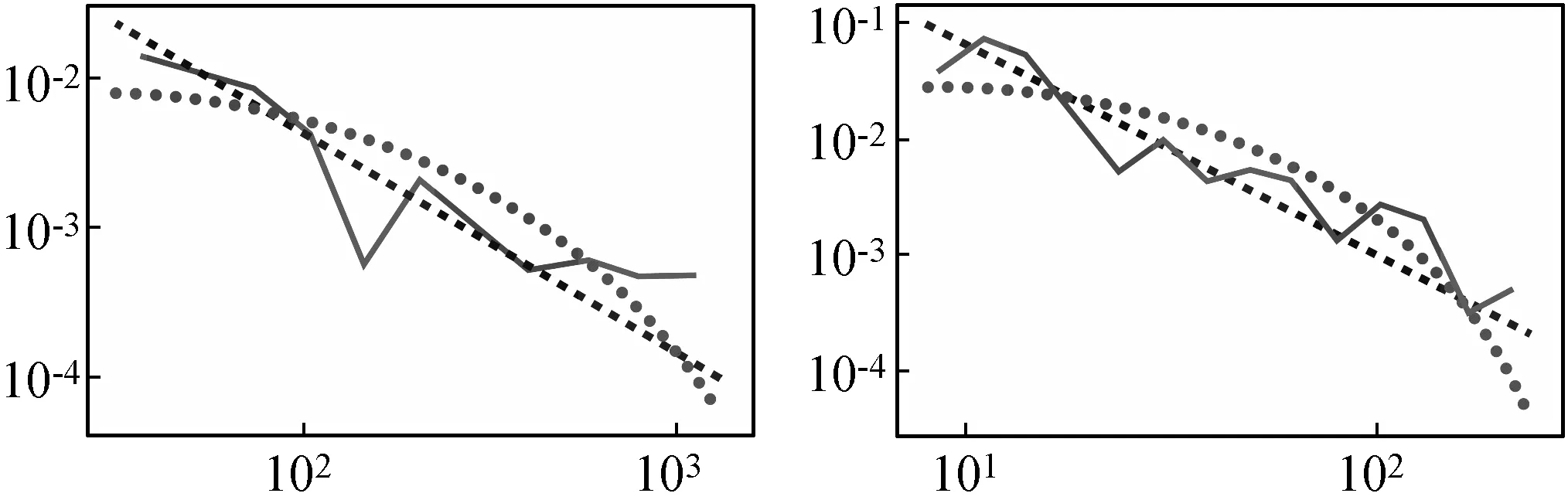
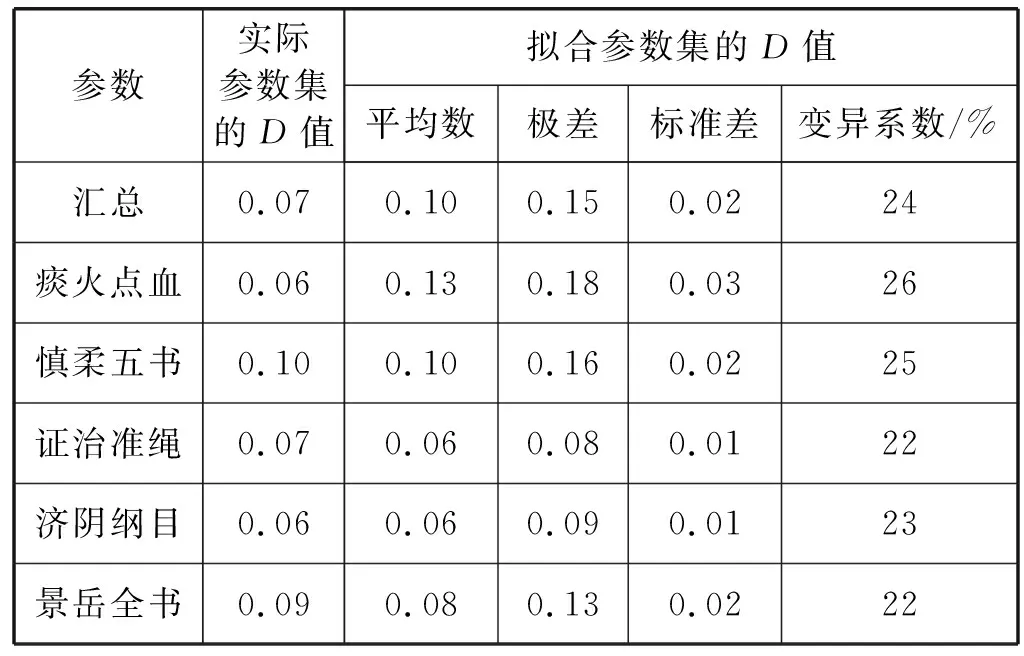
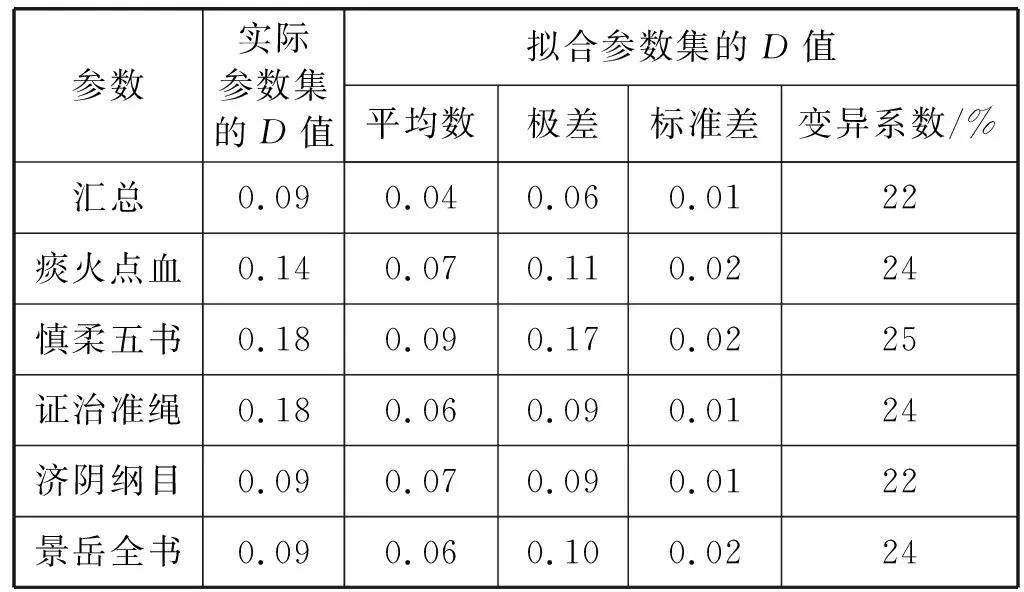
(4) 调整拟合参数集,若n0>ntail,则随机剔除其中n0-ntail个满足x≥xmin的变量,并从实际参数集中随机抽取n-ntail个满足x (5) 检查拟合参数集,保证n0=ntail,且拟合参数集中x (6) 重复步骤(3)-步骤(5),直至生成指定数目的拟合参数集。 拟合参数集的数目S的计算公式为: (8) 式中:λ表示P值的小数点位数。本研究的P值精确到小数点后两位,即λ=10-2,最终计算得拟合参数集的数目应为2 500。 本研究共筛选明代虚劳专著(专篇)89部,整理虚劳方剂2 750首,涉及中药561种,其使用频数合计为31 325次,使用频数排名前20%的高频中药的使用频数累积占比达87%,这提示明代虚劳专著(专篇)中虚劳方剂的中药使用是不均衡的,其使用情况符合二八定律。同时,本研究共挖掘出中药配伍关系22 056种,其度值合计为422 020,度值排名前20%的高度值中药的度值累积占比达88%,提示明代虚劳专著(专篇)中虚劳方剂的中药度值也是不均衡的,其使用情况同样符合二八定律。此外,本研究随机抽取了5部虚劳专著(专篇),包括《痰火点血》《慎柔五书》《证治准绳·虚劳门》《济阴纲目·虚劳门》《景岳全书·虚劳门》,对其方药进行了统计分析:其虚劳方剂分别为25、19、235、95及31首,涉及药物70、35、270、142和82种。此外,本研究分别绘制明代虚劳专著(专篇)及从其中随机抽取的5部虚劳专著中虚劳方剂的中药使用频数及度值的频率直方图,发现其直方图大多具有“重尾”的特征,提示明代虚劳专著(专篇)虚劳方剂的中药使用频数及度值的频率分布可能服从幂律分布。明代虚劳专著(专篇)虚劳方药的描述性统计结果详见表1,中药使用频数的频率分布直方图详见图1,中药度值频率分布直方图详见图2。 表1 明代虚劳专著(专篇)方药的描述性统计结果 (a) 汇总 (b) 痰火点血 (c) 慎柔五书 (d) 证治准绳 (e) 济阴纲目 (f) 景岳全书图1 明代虚劳专著(专篇)中虚劳方剂的中药使用频数的频率分布直方图 (a) 汇总 (b) 痰火点血 (c) 慎柔五书 (d) 证治准绳 (e) 济阴纲目 (f) 景岳全书图2 明代虚劳专著(专篇)中虚劳方剂的中药度值的频率分布直方图 本研究在对明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布进行幂律拟合后发现,其虚劳方剂的中药使用频数的频率分布的r值为22.10,大于0,且Q值小于0.10,提示其中药使用频数的频率分布倾向于服从幂律分布。明代虚劳专著(专篇)中的《证治准绳·虚劳门》《济阴纲目·虚劳门》《景岳全书·虚劳门》的r值皆大于0。其中《证治准绳·虚劳门》《景岳全书·虚劳门》的Q值大于0.10,r值不具备参考价值,暂时不能判断其虚劳方剂的中药使用频数的频率分布是否服从幂律分布;而《济阴纲目·虚劳门》的Q值小于0.1,提示其虚劳方剂的中药使用频数的频率分布倾向于服从幂律分布。另外,《痰火点血》《慎柔五书》的r值小于0,但其Q值皆大于0.10,r值不具备参考价值,暂时不能确定其虚劳方剂的中药使用频数的频率分布是否倾向于服从指数分布。 此外,明代虚劳专著(专篇)中虚劳方剂的中药度值的频率分布的r值为68.02,大于0,且Q值小于0.10,提示其中药度值的频率分布倾向于服从幂律分布。其中的《证治准绳·虚劳门》《济阴纲目·虚劳门》《景岳全书·虚劳门》的r值皆大于0,但其Q值皆大于0.10,r值不具备参考价值,暂时不能判断虚劳方剂的中药度值的频率分布是否倾向于服从幂律分布。而《痰火点血》《慎柔五书》的r值小于0,但其Q值皆大于0.10,r值不具备参考价值,暂时不能判断虚劳方剂的中药度值的频率分布是否倾向于服从指数分布。 明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布在双对数坐标系中的形态与上述结果较为一致:其中药使用频数及度值的频率分布在双对数坐标系中近似于一条直线,提示其中药使用频数及度值的频率分布倾向于服从幂律分布,而从其中随机挑选的5部虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布在双对数坐标系中的形态较不规则,暂时无法判断其倾向于服从哪种分布。 明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布的幂律拟合参数分别见表2及表3,其中药使用频数及度值频率分布在双对数坐标系下的形态分别见图3及图4。 表2 虚劳方剂的中药使用频数频率分布的幂律拟合参数 表3 虚劳方剂的中药度值频率分布的幂律拟合参数 (a) 汇总 (b) 痰火点血 (c) 慎柔五书 (d) 证治准绳 (e) 济阴纲目 (f) 景岳全书图3 虚劳方剂的中药使用频数频率分布的双对数坐标图 (a) 汇总 (b) 痰火点血 (c) 慎柔五书 (d) 证治准绳 (e) 济阴纲目 (f) 景岳全书图4 虚劳方剂的中药度值频率分布的双对数坐标图 以明代虚劳专著(专篇)及从中随机抽取的5部虚劳专著(专篇)虚劳方剂中的中药使用频数及度值作为实际参数集,分别对其进行参数集拟合,生成拟合参数集,进而计算各拟合参数集的D值,并与实际参数集的D值进行比较。研究结果表明,明代虚劳专著及其中的5部虚劳专著(专篇)的中药使用频数及度值的拟合参数集的D值的变异系数皆在22.00%~27.00%之间,拟合参数集的D值的变异程度相近,表明本研究的拟合参数集的生成方法较为稳定,基于同一实际参数集所生成的拟合参数集同质性较高。 通过绘制D值的散点图可以直观地比较实际参数集及其拟合参数集D值的异同。明代虚劳专著(专篇)中虚劳方剂的中药使用频数参数集的D值较其大部分的拟合参数集的D值小,其中的《痰火点血》亦是如此,提示明代虚劳专著(专篇)及其中的《痰火点血》中虚劳方剂的中药使用频数的频率分布服从幂律分布的可能性大;而《慎柔五书》《证治准绳·虚劳门》《济阴纲目·虚劳门》《景岳全书·虚劳门》中虚劳方剂的中药使用频数参数集的D值接近其拟合参数集D值的均值,提示其虚劳方剂的中药使用频数的频率分布服从幂律分布的可能性较大。 明代虚劳专著(专篇)中虚劳方剂的中药度值参数集的D值几乎大于其所有拟合参数集的D值,其中的《痰火点血》《慎柔五书》《证治准绳·虚劳门》《济阴纲目·虚劳门》《景岳全书·虚劳门》亦存在这种情况,提示明代虚劳专著(专篇)及从其中随机抽取的5部虚劳专著(专篇)中虚劳方剂的中药度值的频率分布不服从幂律分布的可能性大。 明代虚劳专著(专篇)中虚劳方剂的中药使用频数参数集及其拟合参数集的D值详见表4;中药度值参数集及其拟合参数集的D值详见表5;中药使用频数实际参数集及其拟合参数集的D值散点图详见图5;中药度值实际参数集及其拟合参数集的D值散点图详见图6。 表4 明代虚劳专著(专篇)中虚劳方剂的中药使用频数的D值 表5 明代虚劳专著(专篇)中虚劳方剂的中药度值的D值 (a) 汇总 (b) 痰火点血 (c) 慎柔五书 (d) 证治准绳 (e) 济阴纲目 (f) 景岳全书图5 明代虚劳专著(专篇)中虚劳方剂的中药使用频数的D值散点图 (a) 汇总 (b) 痰火点血 (c) 慎柔五书 (d) 证治准绳 (e) 济阴纲目 (f) 景岳全书图6 明代虚劳专著(专篇)中虚劳方剂的中药度值的D值散点图 经计算,明代虚劳专著(专篇)中虚劳方剂的中药使用频数参数集的P值为0.69,大于0.10,故而认为其中药使用频数的频率分布符合幂律分布。此外,本研究发现从明代虚劳专著(专篇)中随机抽取的5部明代虚劳专著(专篇)中虚劳方剂的中药使用频数参数集的P值皆大于0.10,其中药使用频数的频率分布皆符合幂律分布,这反映了幂律分布的无标度特性。而明代虚劳专著(专篇)中虚劳方剂的中药度值参数集的P值为0.00,小于0.10,故而认为明代虚劳专著(专篇)中虚劳方剂的中药度值的频率分布不符合幂律分布。另外,随机抽取的5部明代虚劳专著(专篇)中,除《济阴纲目》虚劳方剂的中药度值参数集的P值等于0.10外,其余的4部虚劳专著(专篇)虚劳方剂的中药度值参数集的P值皆小于0.10,其中药度值的频率分布皆不符合幂律分布,表明其分布不具备无标度的特性。明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布的P值详见表6。 表6 明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布的P值 幂律分布具有许多很有趣的特性,比如其频率分布直方图具有“重尾”特性,其频率分布在双对数坐标系中的形态近似于一条直线。在既往的研究中,幂律分布的上述特性常被应用于幂律分布的检验。由于人工观测的方法简单、直观,因此它常被用于幂律分布的初步检验。然而,由于人工观测的方法受观测者主观因素的影响较大,其检验结果往往缺乏客观性及准确性。如本研究发现明代虚劳专著(专篇)及从其中随机挑选出来的5部虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布直方图皆具有“重尾”的特性,明代虚劳专著(专篇)中虚劳方剂的中药度值的频率分布在双对数坐标系中的形态亦近似于一条直线,若仅采用人工观测法进行幂律分布检验,则会得出明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布皆符合幂律分布的错误结论。而计算机模拟仿真检验的结果表明,明代虚劳专著(专篇)中虚劳方剂的中药度值并不符合幂律分布。因此,在实际的幂律检验过程中,除人工观测法外,研究者仍需结合其他的检验手段,以综合评判幂律分布的拟合优度,提高幂律检验的准确性。 本研究发现,明代虚劳专著(专篇)中虚劳方剂的中药使用频数的频率分布符合幂律分布,说明在明代虚劳专著(专篇)中虚劳方剂所涉及的所有中药中,少数中药在虚劳病的辨治过程中获得极大量的使用,而大部分中药仅获得极少量的使用。明代虚劳方药使用频数的频率分布服从幂律分布的现实意义是,在研究明代虚劳专著(专篇)的虚劳方药时,仅需掌握其少部分的高频中药的信息,就能够基本把握其虚劳方药使用的整体情况。此外,本研究亦发现明代虚劳专著(专篇)中虚劳方剂的中药使用频数的频率分布具有无标度特性,其现实意义是,在研究任意一部明代虚劳专著(专篇)时的虚劳方药时,同样仅需掌握其少部分的高频中药的信息,就能够基本把握该部专著(专篇)虚劳方药使用的整体情况。上述研究结果有利于指导中医临床医师及科研人员的临床用药及基础研究,具有重要的现实意义。 本研究发现,明代虚劳专著(专篇)中虚劳方剂的中药度值的频率分布不符合幂律分布,说明其中药配伍关系网络并不是无标度网络。无标度网络中的各节点的度值服从幂律分布,而其节点的择优连接行为是引起各节点度值幂律现象产生的原因[21-22]。明代虚劳专著(专篇)中虚劳方剂的中药度值的频率分布不符合幂律分布,从侧面说明了其中药配伍关系网络中,各节点的连接模式并非择优连接模式,亦即一个新的中药节点在进入中药配伍关系网络时,网络中原有的大度值中药节点对它并不具有绝对的吸引力,新的中药节点并不会优先与大度值中药节点发生连接。明代虚劳专著(专篇)中虚劳方剂的中药配伍关系网络之所以会具有上述特性,是因为临床医师在进行药物配伍、组方治疗虚劳病时,更多的是根据病人的实际症状及病情进行中药的辨证配伍及辨证组方用药,而不会因为某一中药常搭配其他中药组方应用于虚劳病的治疗,就优先选用该味中药。这体现了中医辨证论治的思想,也在某种程度上证实了中医辨证论治的思想确实存在于虚劳病的治疗过程中。 本研究对明代虚劳专著(专篇)中虚劳方剂的中药使用频数及度值的频率分布进行了研究,并采用基于极大似然估计的结合计算机模拟仿真的方法对其进行了幂律拟合、参数估计及幂律分布检验,结果发现明代虚劳专著(专篇)中虚劳方剂的中药使用频数的频率分布服从幂律分布,而其中药度值的频率分布不服从幂律分布。上述发现具有重要的现实意义,有利于指导临床医师及科研人员的临床用药及基础研究,最终造福于虚劳病患者。1.7 拟合参数集数目的估算
2 结果与分析
2.1 描述性统计分析结果

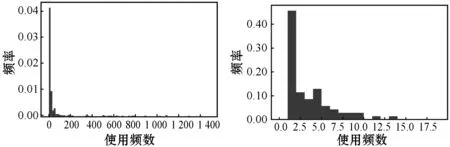
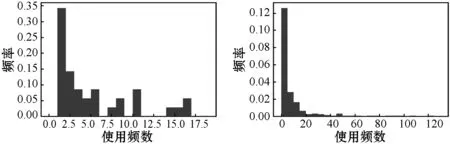
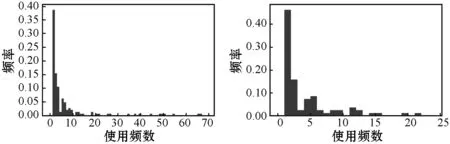
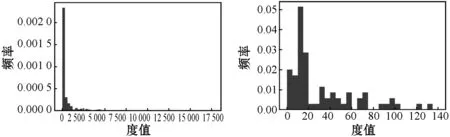
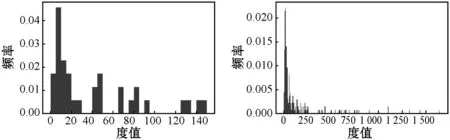
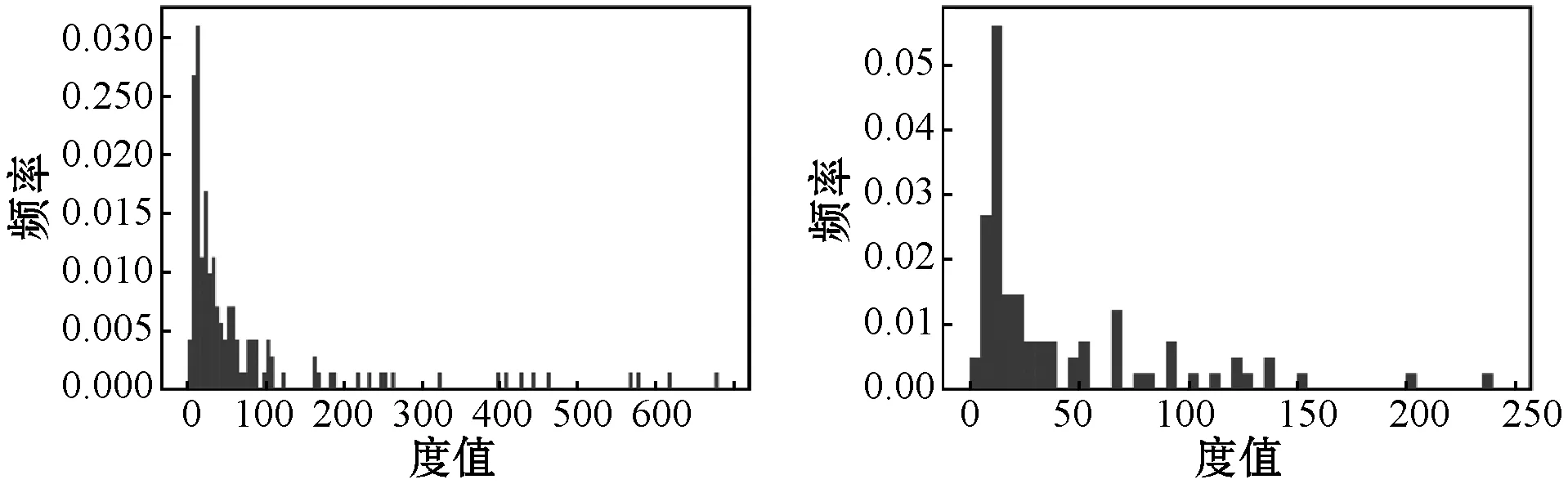
2.2 幂律拟合及参数估计结果

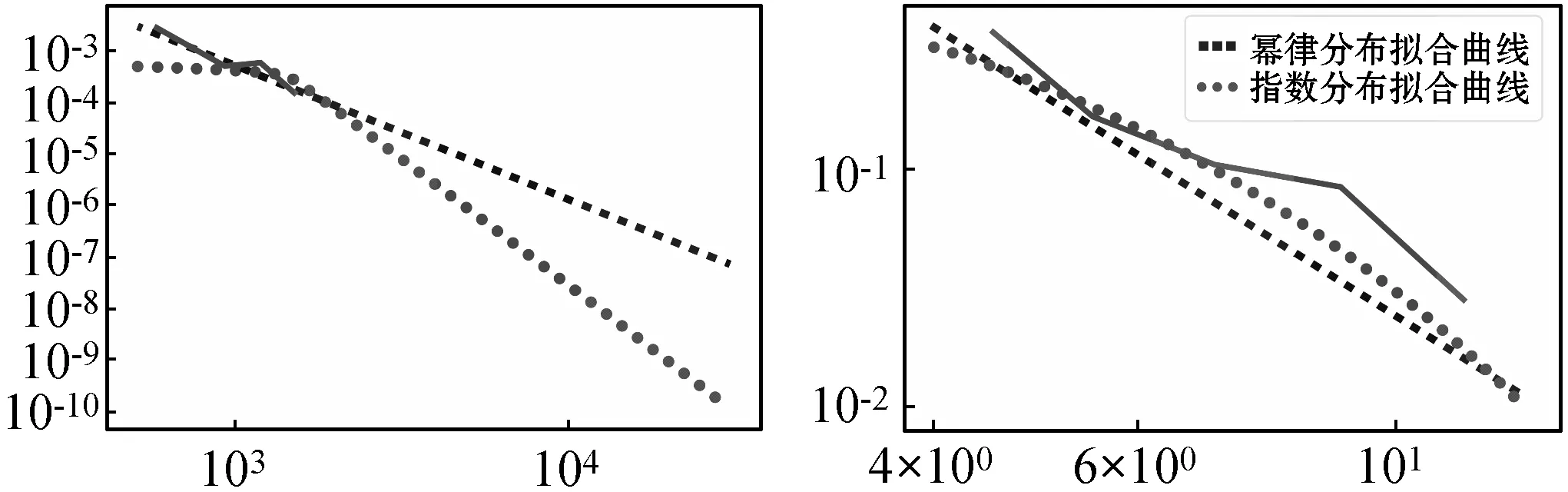
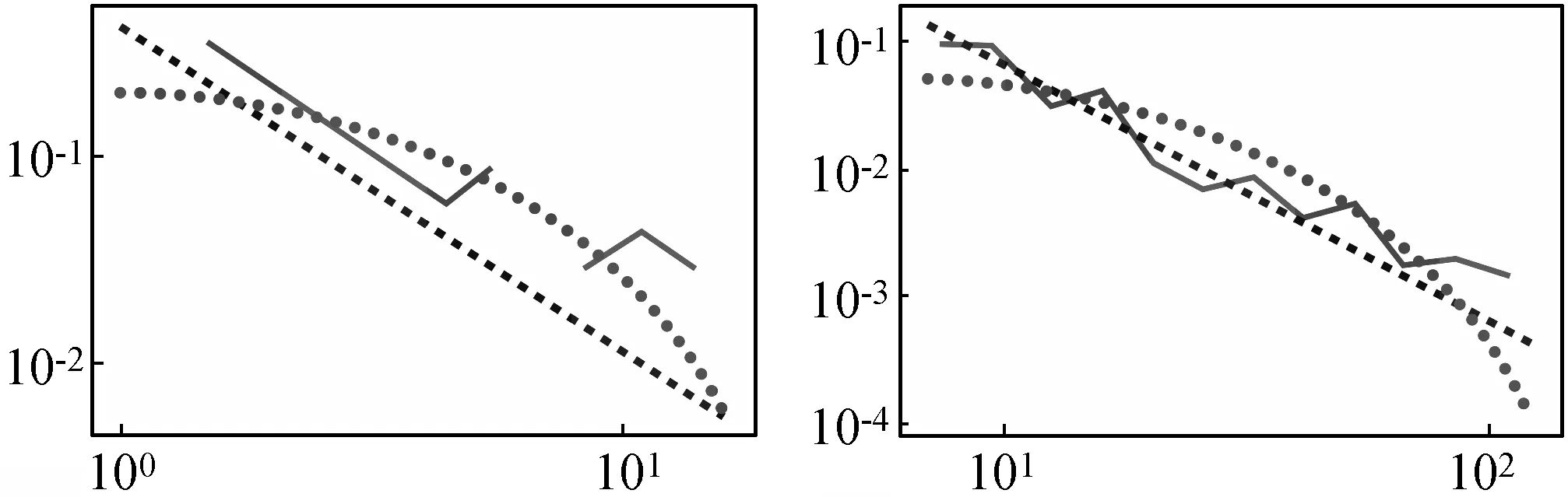
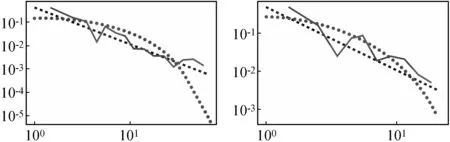
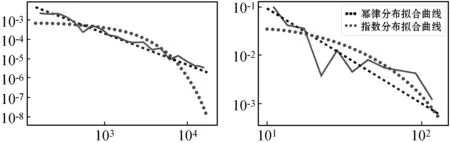
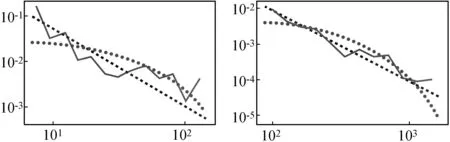
2.3 拟合参数集的生成及其D值计算






2.4 幂律分布检验结果

3 讨 论
3.1 幂律分布检验
3.2 明代虚劳方药使用频数的频率分布
3.3 明代虚劳方药度值的频率分布
4 结 语

