基于小波变换的船舶电力系统绝缘监测方法
姜帅全 朱志宇
(江苏科技大学电子信息学院 江苏 镇江 212000)
0 引 言
在船舶作业过程中,由于自然环境和作业环境的影响,例如化学腐蚀、机械损耗等,容性设备中的绝缘介质容易老化,其绝缘性能也会受到影响。介质损耗因数tanδ可作为重要参数反映容性设备绝缘情况。介质损耗角度是指变压器电场作用下的电流和电压之间的损耗角度,称为介质损耗角度δ,它可以反映电气设备的绝缘情况。但是,设备的绝缘情况在实践过程中由tanδ反映,即公共介质损耗角的切线。在实际作业过程中,由于交变电场的作用,绝缘材料中的内部自由粒子会产生介质极化和导电现象。当电流延迟时,材料内能量损失以热量形式释放。由于热能,绝缘材料在较长的工作时间内可能老化并降低绝缘能力。在这种情况下,船舶电力系统可能面临某些安全风险,必须及时进行绝缘检测以避免故障。
介质损耗角正切值也就是介质损耗因数,其定义:
(1)
式中:P测为被测试品的有功功率;Q测为被测试品的无功功率。
介质损耗角是反映高压电气设备绝缘性能的一项重要的指标。更改的介质损耗角度可以反映绝缘缺陷。绝缘监测对于船舶电力系统的安全性及可靠性具有重大的价值。
1 测量介质损耗角的方法
电气设备介质损耗系数(tanδ)检测方法包括两种,一种基于硬件,另一种基于软件。
1.1 以硬件为主的测量方法
1.1.1过零鉴相法
过零鉴相法用来计算tanδ。在实践中,由于硬件电路可能具有影响检测精度的固有零不平衡,因此通常可以通过在检测周期中将波形向上移至零以上两次来克服这种不平衡。过零鉴相法的缺点是受到波形畸变的严重影响,要求零点精度高,此外过零鉴相法对电网谐波的影响较大[1]。
1.1.2过零点电压比较法
对于电压幅度值相同、频率相同和相位角度稍有不同的正弦电压适用于过零点电压比较法。也就是说,可以通过两个高于零的正弦波之间的电压差异来唯一确定大小和频率相同的两个正弦电压之间的相位差异。过零点电压比较法的优势是不需要严格的A/D转换,且具有良好的抗干扰能力。
1.2 以软件为主的测量方法
介质损耗角度测量方法以硬件为主,仍存在着一些不足,例如电路的硬件要求高,易受站点环境中的电磁干扰和地面电网的谐波干扰。软件分析方法是目前常用的测试方法,其优点是灵活实用,便于信号处理,消除谐波产生的误差,克服了环境对硬件测量方法有较大影响的缺陷[2]。谐波分析、相关系数法和正弦波合法拟合法是主要的软件分析方法。由于不严格要求取样点数的相关系数分析方法的优势,选择相关系数分析方法作为介质损耗因素检测算法。
2 小波变换在绝缘检测中的应用
监测船舶电力系统绝缘情况时,因为船舶电力系统非常复杂,必须在收集过程中纳入环境电磁干扰和频繁出现的严重干扰信号(闪电脉冲、操作冲击等)。极端情况下,当实际电流信号被干扰信号淹没时,监测跟踪信号也更加困难。因此,从高度扰动环境中提取脆弱和有用的信号对于进一步处理至关重要,这对介质损耗系数的测量的准确性有直接影响[3]。在实践中,减少噪声不仅需要研究信号捕捉技术和设计信号电路,更重要的是还需要找到最好的方法来减少信号捕捉所产生的噪声。传统的过滤器是最常用的方法之一,但消除噪声往往会扭曲所需的信号。此外,傅里叶变换也是数字信号处理的一个重要方法,特别是当它被用于处理信号时,效果良好。但是,傅里叶变换不能用于局部分析。短期傅里叶变换在处理非光滑信号时,通过在傅里叶变换中引入窗口函数,并通过窗口平移可局部分析信号。
小波变换的特点是固定的窗口空间和可变的窗口形状,能够在时间和空间上分析信号,克服传统的傅里叶变换的局限性[8]。这种转换原则是傅里叶变换后的又一个重大突破,可以通过传统的傅里叶变换来处理所有的问题。小波变换对某一时刻的频率分布起到决定作用,混合信号由于可将不同频率的信号分为不同频率的信号块,所以具有消除噪声的优点。高次谐波存在于船舶交流电网中,介质损耗角正切值tanδ的准确测量会因为有高次谐波存在而受到影响。小波变化很少受频率偏移的影响,通过良好的噪声消除功能和频率跟踪功能。因此本文选择小波变换,在船舶交流电网中过滤谐波,获得正确的介质损失切值tanδ,及时对设备的绝缘情况进行检测,以便船舶电力系统的安全运行得到保证[4]。
2.1 小波变换的基本理论
小波变换能够很好地处理主要频率为低频信息的信号,与此不同的是小波包变换能够对信号的高频部分做更精细的分解。小波包的定义如下:
给定正交尺度函数φ(t)和小波函数ψ(t),其二尺度关系为:
(2)
进一步推广二尺度方程,定义递推关系:
(3)
式中:hk、gk分别为对应的尺度函数φ(t)和小波函数ψ(t)的滤波器系数。当n=0时,w0(t)=φ(t),w1(t)=ψ(t)。小波包具有平移正交性与w2n和w2n+1正交的关系。
目前的小波库中有许多小波包,不同的小波包的适用情况和性质均不用,在处理不同的问题时应选取合适的小波包。小波母函数和最优小波包基的选取在处理信号时非常关键,两个选取均合适会达到很好的处理效果,有利于下一步运算的进行[5]。
因船舶电网的高次谐波分量会影响介质损耗角的测量精度,若要准确进行绝缘检测则需提取出基波信号,滤除高次谐波。采用尺度分析的小波包变换可以在信号的不同位置得到最佳时域分辨率和频域分辨率,实现电压电流基波信号与高次谐波信号的分离,是一种有效的分析工具。
基于小波包变换谐波检测是将船舶岸电电网中含有高次谐波的电压和电流经A/D采样将信号离散化,再选取合适的小波包,将基波信号与各高次谐波分解到不同频带的子频带信号中,将检测出的电压电流基波信号体现在子频带区域中,其余的高次谐波则在其余子频带区域体现。小波包分解与重构得到基波分量的方法是对基波分量的子频带区域重构,达到基波信号与谐波信号的分离[6]。
由以上理论,可以将船舶电网中的电压、电流信号展开为小波基函数权值相加的线性组合。以电压信号为例,可以将电压信号展开如下:
(4)
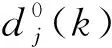
船舶电力系统中的电压信号VRMS的值在第j层分解可以用小波变换系数(Wavelet Transform Coefficients,WTCs)。
(5)
式(6)可近似如下:
(6)
电压v(t)的RMS值表示如下:
(7)
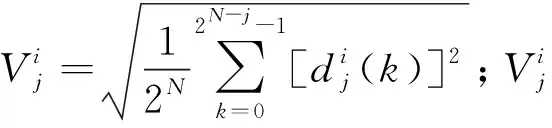
2.血清淀粉酶、脂肪酶测定:采用比色法检测淀粉酶、脂肪酶,试剂盒购自南京建成生物工程研究所,按说明书操作。
(8)
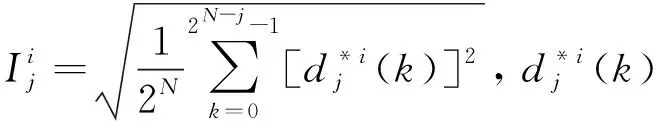
2.2 基于Daubechies(dbN)小波分析
小波(Daubechies)简写为dbN,其阶数用N表示,是由小波分析学者Daubechies提出的。当N=1时dbN具有对称性,N≠1时则不具备对称性的性质。此外,当N=1时dbN表达式可以确定,N≠1时转换函数h的平方模可明确,但表达式不可明确。
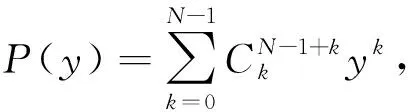
(9)
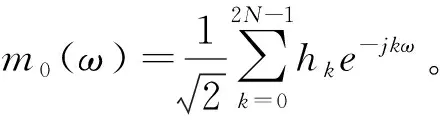
Daubechies小波有以下特点:可以由所谓“尺度函数”φ(t)求出小波函数ψ(t),尺度函数φ(t)是一种长度度有限的低通函数,支撑域在t=0~(2N-1)范围内。常用于电能质量分析的db4小波函数的波形图和滤波器如图1和图2所示。
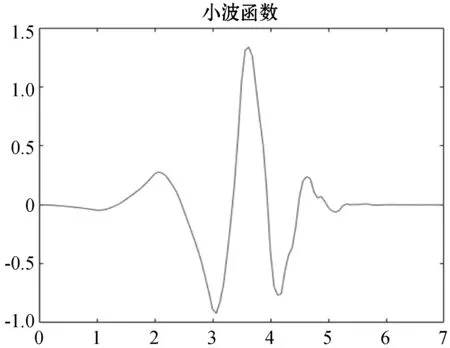
图1 db4小波函数
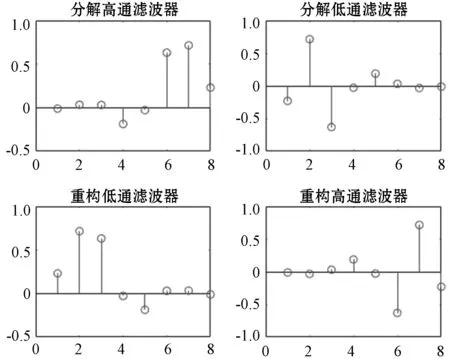
图2 db4小波函数小波滤波器
3 基于小波和相关函数分析的介损测量方法
3.1 相关函数介损测量算法
所谓相关函数法是根据船舶交流电网中的电压u=Umsin(ωt+φu)和电流i=Imsin(ωt+φi)的自相关函数和互相关函数获得船舶岸电系统中设备的介损角的。其中电压电流的自相关函数与互相关函数如式(10)所示。
(10)
式中:T为整周期,N为T内的采样点数。在实际算法中,相关算法的离散时间表达式如下:
(11)
介损角为:
(12)
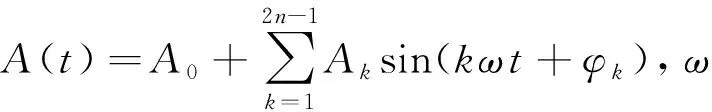
3.2 对相关函数介损测量的改进
以基波频率为60 Hz、电压为440 V的低压船舶电力系统为例,谐波主要是2n+1(n=1,2,…)等奇数次谐波,考虑到谐波衰减并且频率越高衰减越快,现将电力系统中基波电压及谐波信号设置如下:
基波电压信号为:
U1=440×sin(120×π×t)
(13)
三次谐波为:
U3=0.05×440×exp(-15×t)×
sin(360×π×t+π/3)
(14)
五次谐波为:
U5=0.03×440×exp(-20×t)×
sin(600×π×t+π/5)
(15)
七次谐波为:
U7=0.03×440×exp(10×t)×
sin(800×π×t+π/4)
(16)
九次谐波为:
U9=0.02×440×exp(5×t)×
sin(1 080×π×t+π/6)
(17)
十一次谐波为:
U11=0.01×440×exp(-1.5×t)×
sin(1 320×π×t+π/4)
(18)
原始电压信号图与幅频特性图分别如图3和图4所示。
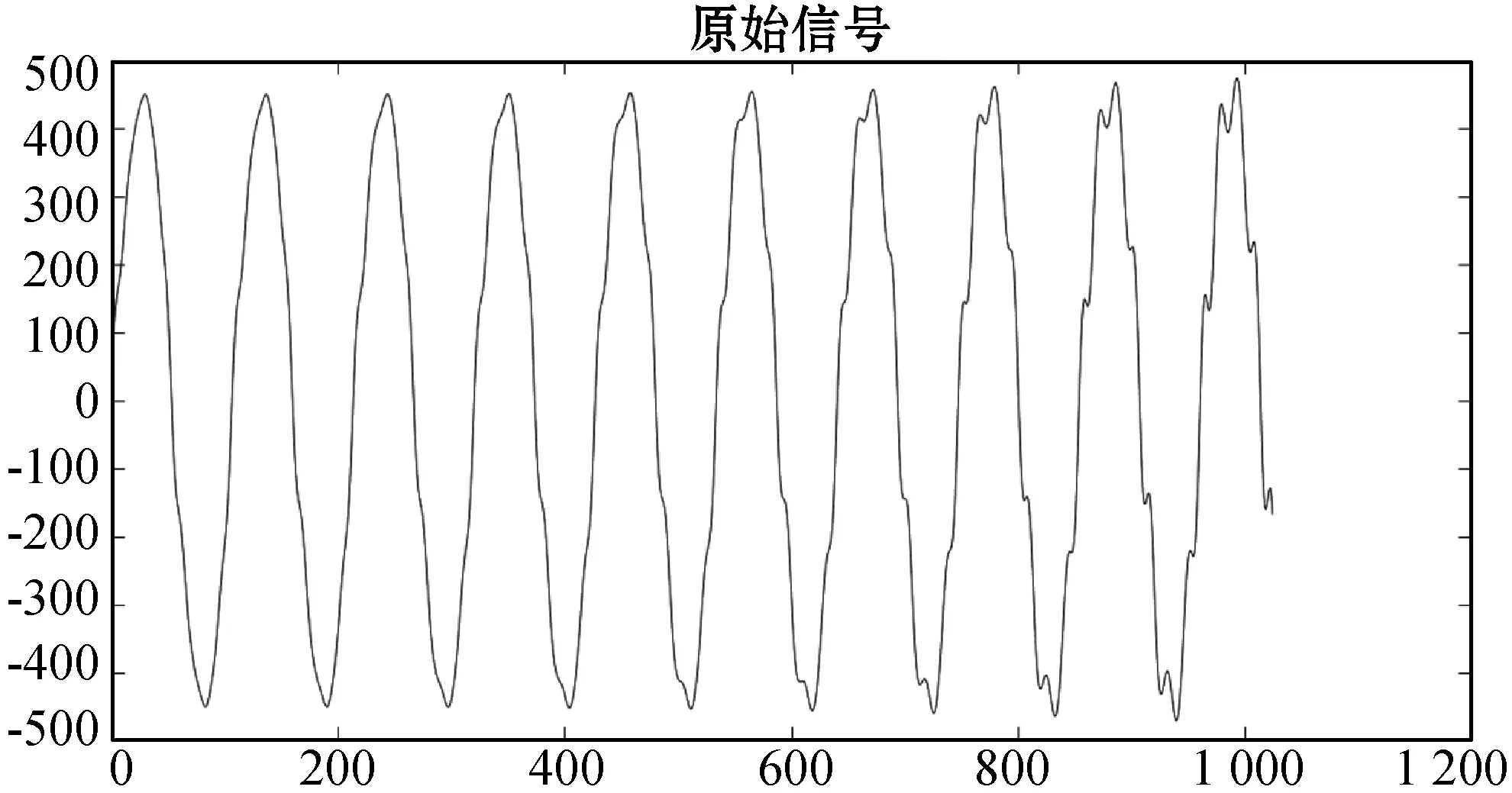
图3 原始电压信号
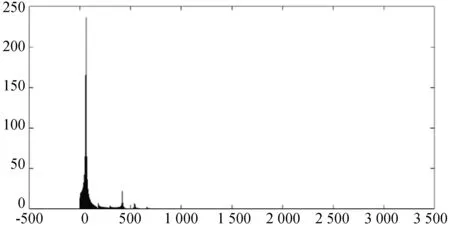
图4 原始电压信号幅频特性图
以此基波频率为60 Hz的船舶电力系统为例,船舶交流电网中有3~11次奇次谐波,需要将以上谐波全部滤除得到基波60 Hz的信号。设模拟采样频率为6 400 Hz,可以还原到频率为3 200 Hz的信号,对信号进行第一次Mallet分解可以还原的信号分为低频概貌(0~1 600 Hz)和高频细节(0~3 200 Hz),再将此低频概貌信号进行一次Mallet分解依旧可以得到低频概貌(0~800 Hz)和高频细节(800~1 600 Hz)以此类推,进行5次Mallet分解可以滤除高次谐波得到60 Hz的基频电流信号[7]。示意图如图5所示。
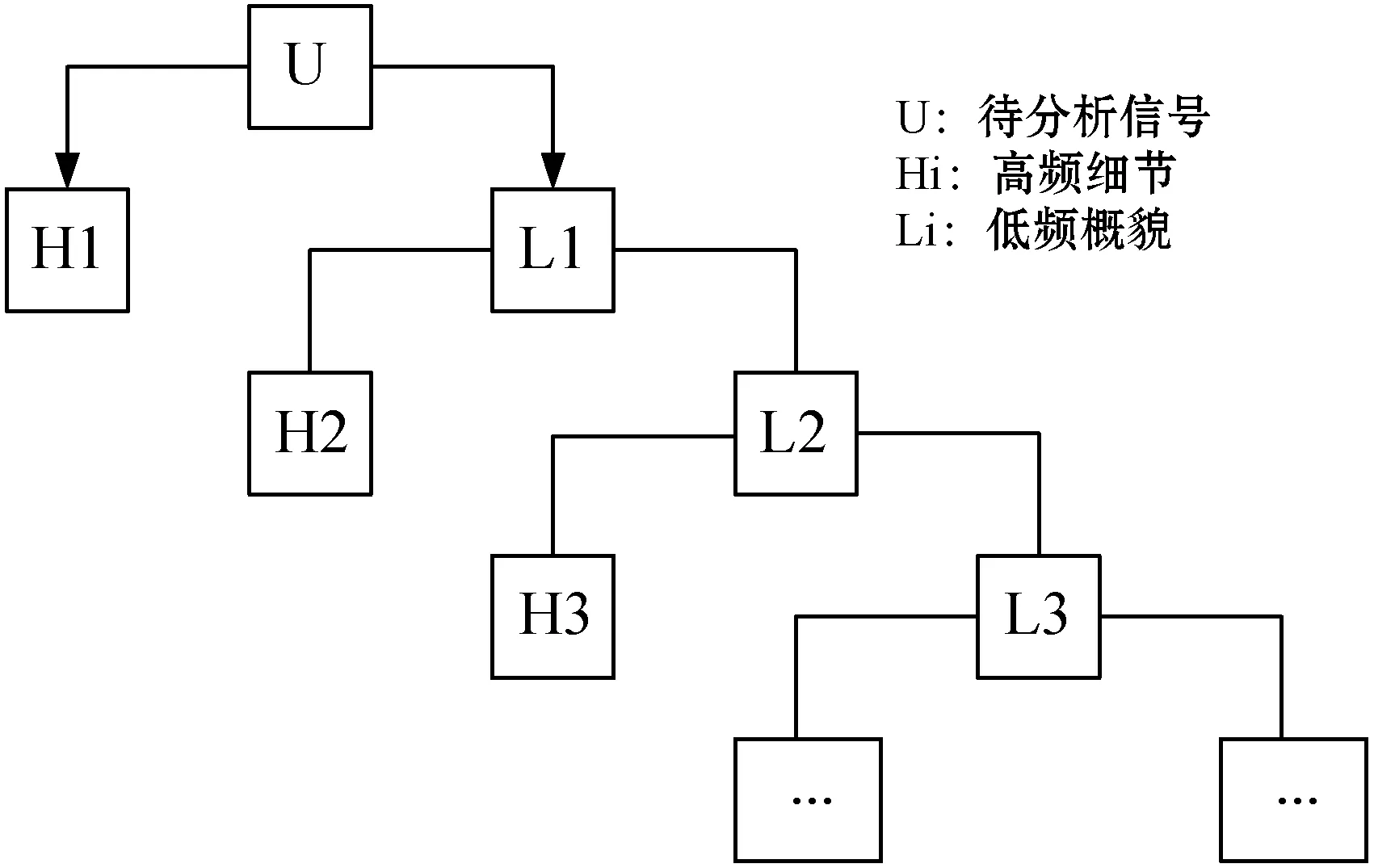
图5 Mallet分解示意图
以6 400 Hz的采样频率,用Mallet分解进行5次分解,五次分解后的低频概貌信号中含有60 Hz的基波电流信号,然后再经过5次小波重构,就可得到船舶交流电网中的电压基波信号。在小波重构的过程中,为了保证重构信号与真实信号之间的准确性、减少失真,即保证基波信号与谐波信号之间完全分离,则要求小波变换中使用的小波基具有以下特性:
① 紧支性。保证检测的精度。
② 正交性。使得基波谐波能够分离。
③ 高阶消失矩。使计算量有限。
④ 对称性。避免信号失真。
本文选择dbN小波包,N取14,即选取的小波具有十四阶消失矩,将前文中的原始电压信号进行小波去噪,即对原始信号进行5次分解和重构后得到船舶电力系统中的60 Hz基波电压信号。原始信号和滤波后信号如图6所示。
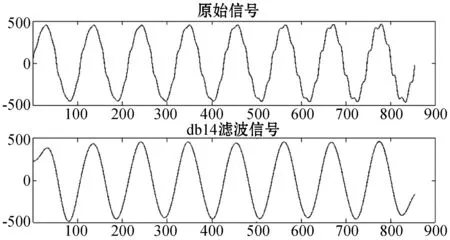
图6 db14滤波效果图
重构后的基波信号的幅频特性图如图7所示。

图7 重构低频信号的幅频特性
4 实验与结果分析
本文使用MATLAB进行基于相关函数分析法和小波变换去噪的介质损耗角测量仿真实验,电压和电流设置如下:
u(t)=sin(ωt+φu1)+0.02sin(3ωt+φu3)+
0.012 5sin(5ωt+φu5)+0.007 5sin(7ωt+φu7)
(19)
0.012 5sin(5ωt+φi5)+0.007 5sin(7ωt+φi7)
(20)
式中:ω=2πf,f=60 Hz;φu3、φu5、φu7、φi3、φi5、φi7为各谐波的相位角,φu1、φi1为基波电压、电流信号的初相角。本文通过仿真对比了过零鉴相法和经小波去噪后再使用相关分析法计算的各介质损耗角,其中,过零鉴相法的Simulink建模如图8所示。
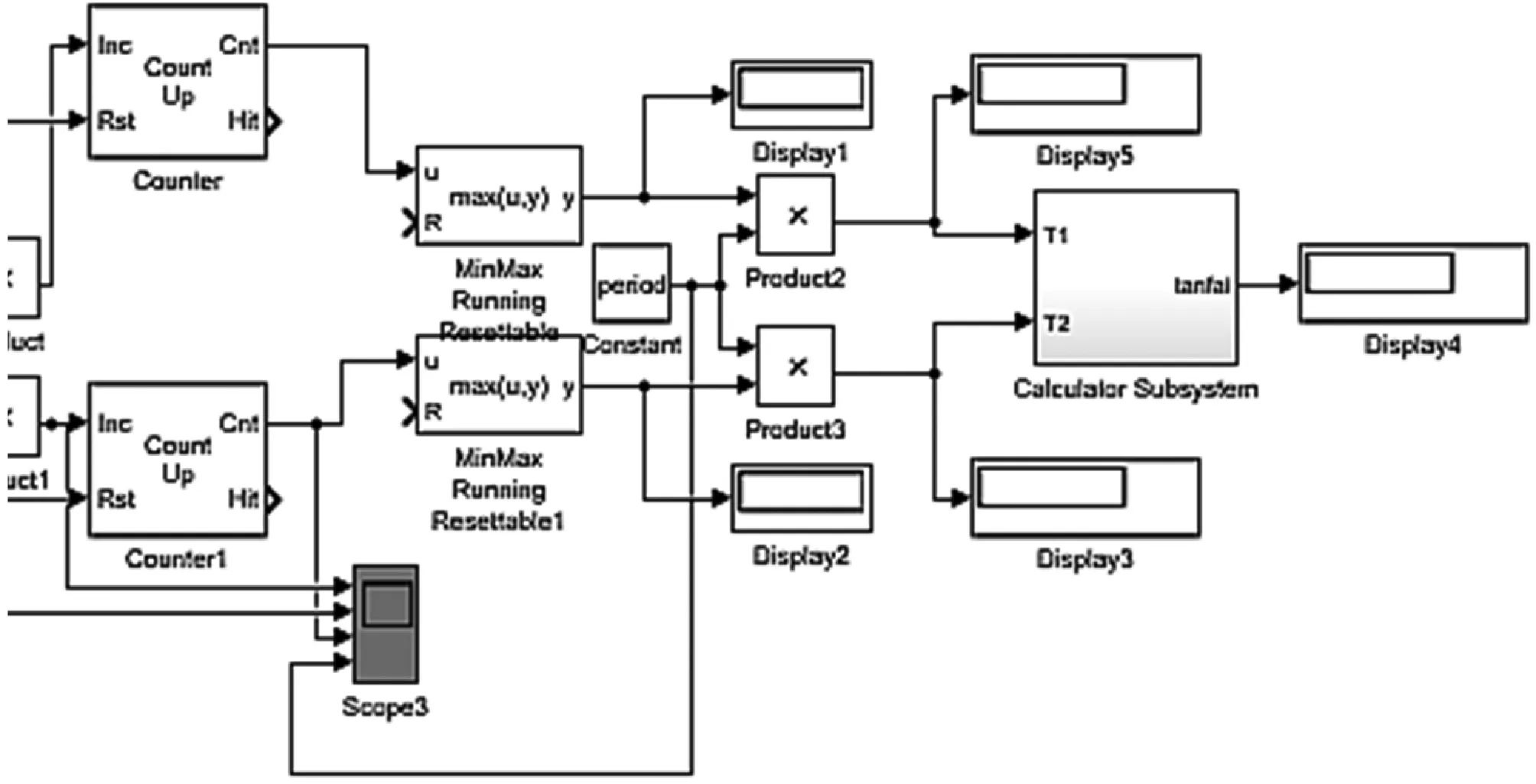
图8 过零鉴相法Simulink模型图
实验结果对比如表1和表2所示,结果表明经小波变换去噪后再使用相关分析法计算的各介质损耗角的测量方法绝对误差和相对误差都比已有软件检测方法(谐波分析法)好,具有更高的测量精度。
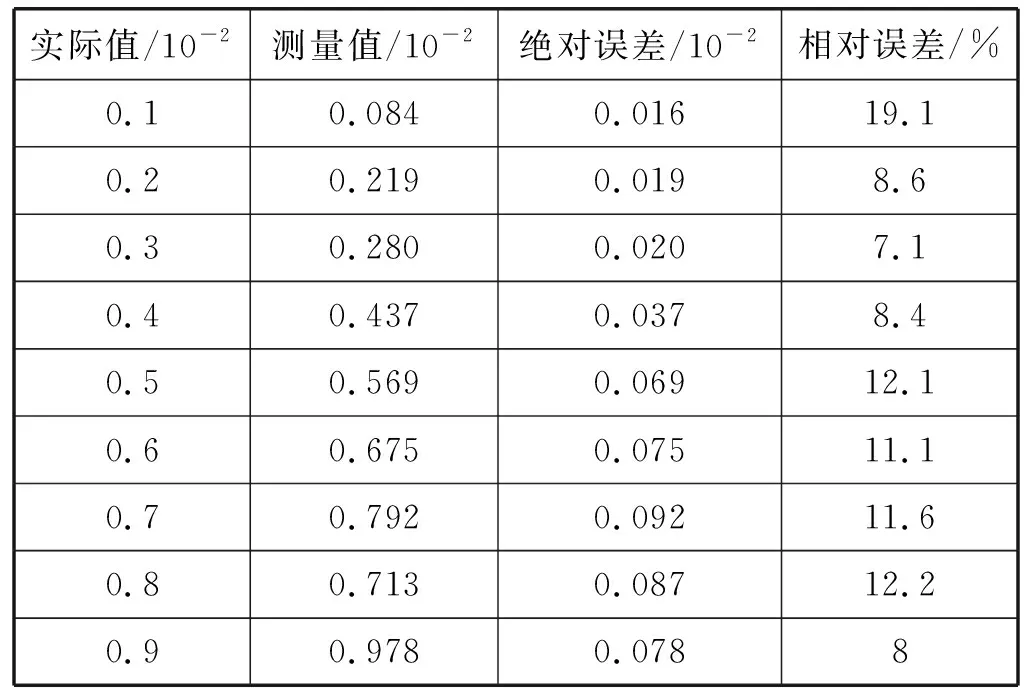
表1 δ角变化时过零鉴相法计算结果
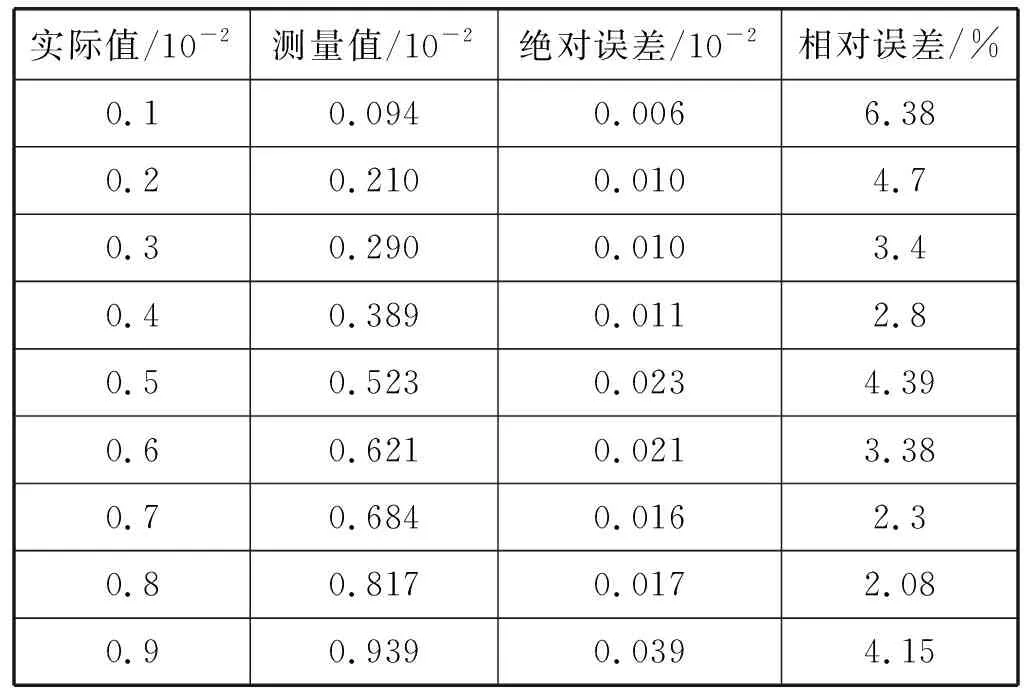
表2 δ角变化时改进相关系数分析法计算结果
5 结 语
本文在分析了介质损耗角的测量方法及影响介质损耗角测量准确度的因素后,使用小波变换,选取合适的小波基对原始电压电流信号进行分解和重构,滤除了船舶电网中的谐波,提取出电压电流的基波,选取相关函数分析法通过基波电压电流信号的自相关函数和互相关函数进行介质损耗角的计算。实验表明用此方法计算的绝缘介质损耗角准确率较高,能更好地监测船舶电力系统中的容性设备绝缘情况,对绝缘故障能够及时发现和处理。本文所提出算法能更好地完成船舶电力系统的绝缘监测工作。

