基于多距离度量kNN模型的森林蓄积量反演

吴胜义，王义贵，王 飞，李伟坡

（1.国家林业和草原局 西北调查规划设计院，陕西 西安 710048；2.旱区生态水文与灾害防治国家林业局重点实验室，陕西 西安 710048；3.中南林业科技大学，湖南 长沙 410004）

森林蓄积量是森林资源经营管理和森林生长质量评价的重要指标。森林蓄积量可以直接反映森林生态系统的健康状况，是森林固碳能力的重要体现[1-2]，对区域森林蓄积量进行估测对快速掌握森林生态系统质量具有重要意义[3]。

遥感技术的应用极大地提高了森林蓄积量的调查效率，利用遥感数据源结合实测样地调查数据进行森林蓄积量反演已经成为国内外研究的热点[4-5]。然而，反演模型的选择一直是影响森林蓄积量反演精度的重要因素。目前，常用的森林蓄积量反演模型主要以参数模型和非参数模型为主[6]。参数模型易于实现，可以直观地表现遥感变量与森林蓄积量之间的定量关系。以多元线性回归为代表的参数模型在森林参数估测上已经得到了广泛应用。此外，非参数模型，例如kNN和随机森林等机器学习算法由于不需要数据有固定的分布趋势，且在小样本上也具有较好的估测效果，已经被证明具有较高的应用潜力[7-8]。其中，kNN模型由于易于实现且效果较好，已经被证明可以成功地用于森林蓄积量反演。郑刚等[9]发现在进行参数优选后，利用kNN模型进行亚热带地区森林蓄积量的遥感估测精度要明显优于传统方法。宋亚斌等[10]以湖南省湘潭县为研究区，利用kNN模型成功地进行了森林蓄积量反演。蒋馥根等[11]利用方差速率变化结合kNN模型对旺业甸林场森林蓄积量进行反演，结果表明kNN模型应用于森林蓄积量反演具有较大的潜力。然而，目前对于kNN估测中的距离度量讨论较少，本研究将利用多种距离度量建立kNN模型进行森林蓄积量反演，以探索距离度量对于kNN在森林蓄积量反演上的效应。

本研究以Sentinel-2 多光谱影像为数据源，结合韩城市森林资源调查实测数据，建立多元线性回归模型、支持向量机模型、随机森林模型和基于多种距离度量的kNN模型对研究区森林蓄积量进行遥感估测。最终选择估测精度最高的模型进行韩城市森林蓄积量反演和空间分布制图，以期为森林蓄积量遥感反演提供参考。

1 材料与方法

1.1 研究区概况

韩城市位于陕西省东部，位置为110°07′09″～110°37′24″ E，35°18′50″～35°52′08″N。北 依 宜川，西邻黄龙，南接合阳，东隔黄河，总面积约1 621 km2。地势西北高，东南低，中部浅山区多为黄土丘陵，境内山原川滩等地貌类型兼有，深山和浅山丘陵占总面积的69%。韩城市处于暖温带半干旱区域，属大陆性季风气候，四季分明，气候温和，光照充足，降水量较多。年平均气温13.5℃，年均降水量559.7 mm，无霜期209 d，年日照2 436 h。春夏季易发生干旱，夏季阵雨多、强度大，水土流失严重。目前全市森林覆盖率为45.3%，主要树种为落叶松Larix gmelini和刺槐Robinia pseudoacacia等。研究区位置及样地分布如图1所示。

1.2 遥感影像预处理及森林蓄积量数据获取

研究使用的遥感数据源为Sentinel-2 MSI数据，获取时间为2018年10月12日，云量小于5%，于欧洲航天局（European Space Agency，ESA）官方网站获取数据（https://scihub.copernicus.eu/）。遥感影像预处理能校正遥感成像过程中由于大气环境、地形起伏和传感器自身影响等产生的误差，以获取更准确的影像信息[12]。本研究利用Sen2cor软件对获取的Sentinel-2数据进行辐射定标、大气校正等预处理，将所有的像元值转换为地表反射率。最终，选择空间分辨率为10 m和20 m的单波段共计10个波段用于后续的森林蓄积量反演。

根据韩城市2018年更新的森林资源二类调查数据，在乔木林地范围内采用随机抽样设置100个大小为30 m×30 m的样地进行森林蓄积量统计，样地分布如图1所示。最终将小班蓄积量转换为单位公顷蓄积量（m3/hm2），对所有样地蓄积量数据进行统计分析，结果如表1所示。

表1 样地蓄积量统计结果Table 1 Statistical results of the stock volume in sample plots

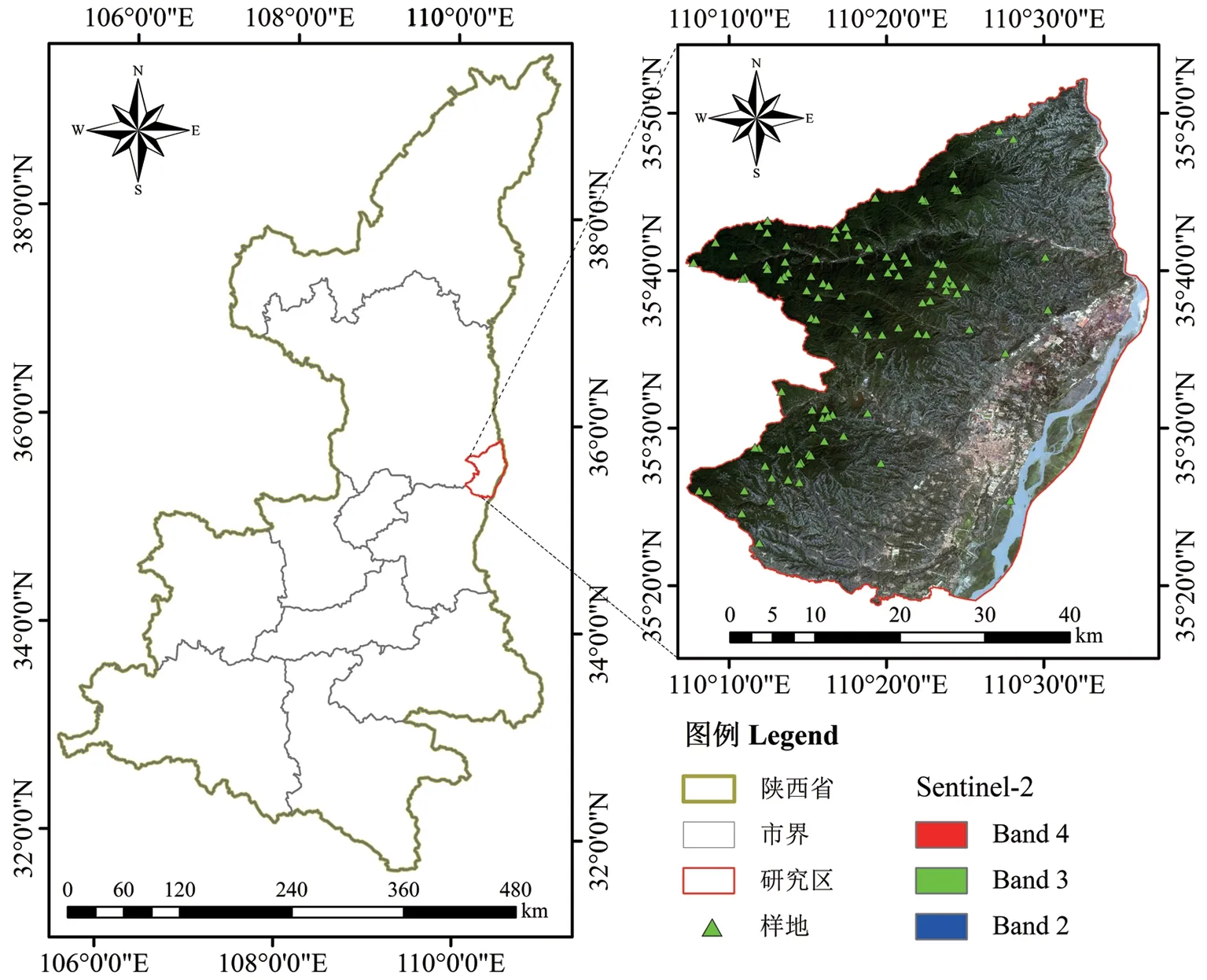
图1 研究区位置图及样地分布Fig.1 Location and plot distribution of the study area

1.3 遥感特征变量提取及筛选

研究共选取了Sentinel-2 中包括10 m和20 m空间分辨率的10个单波段作为光谱变量提取的信息源。提取单波段反射率、波段比值和常用的植被指数作为光谱变量。植被指数已经被证明可以有效地用于森林参数估测，研究提取了归一化植被指数（Normalized different vegetation index，NDVI）[14]、大气抗阻植被指数（Atmospherically resistant vegetation index，ARVI）、增强型植被指数（Enhanced vegetation index，EVI）和红绿植被指数（Red green vegetation index，RGVI）等常见的植被指数[12]。此外，红边归一化植被指数[15]（Red-edge normalized difference vegetation index，RENDVI）和红边叶绿素指数[16]（Red-edge chlorophyll index，RECI）[12]也被提取用于比较红边波段的有效性。纹理特征已经被证明可以有效地用于森林蓄积量反演，研究利用灰度共生矩阵提取所有波段的纹理特征信息[13]。研究提取的所有特征变量的计算公式如表2所示。

表2 遥感特征变量提取Table 2 Variable extraction of remote sensing features

利用统计软件R语言计算所有特征变量与森林蓄积量之间的Pearson相关系数（Pearson correlation coefficient）矩阵。选择与森林蓄积量显著相关的特征变量进行线性逐步回归筛选。为了提高变量筛选的可靠性，方差膨胀因子（Variance inflation factor，VIF）被用于减少变量之间的共线性[8]，VIF阈值设为10。此外，重要性评价也将作为对比进行变量筛选。重要性评价是基于随机森林算法实现的，能够提供所有特征变量的重要性排序，这对从众多特征变量中选取适合反演的特征变量尤其有用[17]。由于森林生态系统的复杂性，非线性特征变量筛选方法具有极大的潜力[18]。

利用线性逐步回归和重要性评价对所有的特征变量进行筛选，结果用于建立森林蓄积量反演模型进行精度比较。

1.4 森林蓄积量反演模型

1.4.1 多元线性回归

多元线性回归（Multiple linear regression，MLR）能定量地描述多个遥感变量与森林蓄积量的关系，作为参数模型的代表，由于方程形式简洁，易于实现，已被广泛用于森林参数估测[6]。多元线性回归模型一般形式为：

式（1）中：Yi为响应变量，X1，X2，…，Xi为解释变量，β1，β2，…，βi为回归参数，β0为常数项，μ为残差项。

1.4.2 非参数模型

支持向量机（Support vector machine，SVM）是一种基于监督学习对数据进行二元分类的分类器，可以通过构建核函数进行非线性估测。常见的核函数包括线性核函数、多项式核函数和高斯核函数。SVM计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这可以有效地避免维数灾难。

随机森林（Random forest，RF）是基于集成学习思想，通过快速构造大量的决策树来进行建模预测。RF学习过程快速，泛化能力强，对于大部分数据集可以平衡误差。此外，随机森林可以评估变量对于模型构建的相对重要性，这可以更好地理解模型的逻辑以及进行高效的特征变量选择[8]。

k最 近 邻（k-nearest neighbor，kNN）指 与预测样本最近的k个样本。kNN是将邻居样本属性的平均值赋给预测样本以得到预测结果。利用kNN模型进行预测时，首先得到预测样本与其他所有已知样本之间的距离排序，确定与预测样本距离最近的k个已知样本的属性，最终根据既定的决策规则进行预测[7]。k值大小和距离度量是影响kNN模型估测效果的主要因素。k值过小将产生噪声对结果产生影响，过大时模型的近似误差会增大[9]。此外，距离度量直接决定用于预测的样本，常用的距离度量有欧几里得度量（也称欧氏距离）（Euclidean metric）、曼哈顿距离（Manhattan distance）和马氏距离[19]（Mahalanobis distance），距离度量计算公式如式（2）～（4）所示。本研究为了探索不同的距离度量对kNN模型的估测影响，将同时基于3种距离构建kNN模型用于森林蓄积量估测。最终，与多元线性回归、支持向量机模型和随机森林模型进行对比分析，以确定研究区森林蓄积量最优估测模型。

式中：D1、D2和D3分别表示欧氏距离、曼哈顿距离和马氏距离，x1、x2、y1和y1分别为2个样本的光谱值。式（4）中：X为向量样本，T表示矩阵转置，均值记为向量μ。

1.5 精度评价指标

采用留一交叉验证（Leave-one-out cross validation）对模型估测效果进行精度验证，以保证尽可能多的样本进入模型，提高模型的稳定性和可靠性[8]。研究选择决定系数R2[19]（Coefficient of determination）、均方根误差[20]（Root mean square error，RMSE）、相对均方根误差（Relative root mean square error，RRMSE）和平均绝对误差（Mean absolute error，MAE）作为精度评价指标。所有指标计算公式如式（5）～（8）所示：

式中：yi表示森林蓄积量实测值，表示森林蓄积量模型预测值，表示实测森林蓄积量均值，n表示样本数量。

2 结果与分析

2.1 特征变量筛选结果

经过相关系数矩阵计算，与森林蓄积量显著相关的特征变量共有57个（P＜0.05）。利用线性逐步回归结合方差膨胀因子最终得到的特征变量组合为RECI、SR34和SR53，多元线性回归的模型统计量如表3所示。

表3 多元线性回归模型统计量Table 3 Multiple linear regression model statistics

重要性评价能对所有特征变量在模型估测上的贡献进行度量，从而得到更重要的变量进行建模。本研究利用R语言randomForest包对所有变量进行重要性计算并排序，部分变量重要性排序如图2所示，重要性最高的变量为RENDVI。此外，SR65、NDVI、B3和SR56也获得了较高的重要性。最终将利用这5个变量建立支持向量机、随机森林和kNN等非参数模型进行森林蓄积量估测。

图2 部分变量重要性排序Fig.2 Importance ranking of partial variables

2.2 森林蓄积量估测结果

利用多元线性回归、支持向量机模型、随机森林模型和基于多种距离度量构建的kNN模型对研究区森林蓄积量进行估测，模型结果如表4所示。非参数模型相比多元线性回归模型估测精度有显著提高，支持向量机模型和随机森林模型估测结果相似，基于欧式距离、曼哈顿距离和马氏距离构建的kNN模型的RMSE相比多元线性回归分别降低了24.1%、28.2%和29.9%。在3种距离度量中，基于马氏距离构建的kNN模型估测精度最好，R2为0.66，RMSE为10.02 m3/hm2。

表4 森林蓄积量估测模型精度比较Table 4 Precision comparison of forest stock volume estimation models

图3为利用多元线性回归、支持向量机、随机森林和基于多种距离度量构建的kNN模型得到的预测值和实测蓄积量值之间的拟合图。多元线性回归模型存在大量的高估和低估值，预测值随机性低，估测效果较差；基于欧式距离、曼哈顿距离和马氏距离构建的kNN模型拟合效果相似，但是高估和低估现象相对于多元线性回归模型有显著改善。其中，基于马氏距离的kNN模型拟合效果最好，模型预测值基本呈随机分布。

图3 森林蓄积量模型拟合Fig.3 Fitting diagram of forest stock volume models

2.3 最优模型森林蓄积量反演

以Sentinel-2多光谱遥感影像为数据源，结合韩城市森林蓄积量实测数据，并利用基于马氏距离的kNN模型对研究区进行森林蓄积量反演，反演结果如图4所示。研究区西北部地区的森林生长情况较好，森林覆盖率较高，蓄积量也分布较大。西南部地区蓄积量值次之。东部和南部地区主要是水域和建筑用地，森林分布较少，几乎无森林蓄积量分布。基于马氏距离的kNN模型森林蓄积量反演结果与研究区实际情况基本一致，反演效果较好，能满足反演需求。

图4 研究区森林蓄积量反演Fig.4 Forest stock volume inversion of the study area

3 结论与讨论

3.1 结 论

以韩城市实测森林蓄积量数据为基础，结合Sentinel-2多光谱影像，利用多元线性回归、支持向量机模型、随机森林模型和基于欧式距离、曼哈顿距离和马氏距离构建的kNN模型对研究区进行森林蓄积量反演，结论如下：1）利用kNN模型进行森林蓄积量估测的精度显著优于多元线性回归模型。基于欧式距离、曼哈顿距离和马氏距离构建的kNN模型的均方根误差相比多元线性回归分别降低了24.1%、28.2%和29.9%；2）在支持向量机模型、随机森林模型和基于3种距离度量的kNN模型中，基于马氏距离构建的kNN模型估测精度最高。决定系数R2为0.66，均方根误差RMSE为10.02 m3/hm2，相对均方根误差RRMSE为18.31%，平均绝对误差MAE为8.03 m3/hm2；3）基于马氏距离的kNN模型的森林蓄积量反演结果与研究区实际情况基本一致，反演效果较好，能满足反演需求。

3.2 讨 论

研究使用的Sentinel-2遥感数据源是2015年6月发射的多光谱卫星，空间分辨率包括10、20和60 m，能满足多种反演需求[21]。Sentinel-2包含3个对植被冠层较敏感的红边波段，能有效地进行森林参数反演[12]。红边波段已经被证明对森林参数估测有效，通过红边波段构建的红边植被指数与森林蓄积量、生物量等参数具有较强的相关性[22]，研究区提取的归一化红边植被指数RENDVI取得了最高的重要性。此外，通过线性逐步回归筛选的变量中也包括叶绿素红边指数RECI，证明了红边波段对森林蓄积量估测具有较高的敏感性。

线性逐步回归是常用的特征变量筛选方法，一般需要特征变量与森林蓄积量之间具有较高的相关关系，然而对于实际复杂的森林状况可能难以满足估测要求。重要性评价可以量化所有变量对于模型的贡献程度，从而通过重要性排序得到合适的特征变量组合，重要性评价结合非参数模型进行森林蓄积量反演具有极大的潜力[21]。距离度量方式能显著影响kNN模型的估测效果，蒋馥根等[11]利用距离倒数加权构建方差优化kNN模型，显著提高了森林蓄积量的估测精度。谢福明等[23]基于遗传算法结合不同的距离度量对优化的kNN模型进行优化，实现了高山松地上生物量高精度估测。本研究基于欧式距离、曼哈顿距离和马氏距离分别构建的kNN模型估测效果具有一定的差异，其中基于马氏距离构建的kNN模型精度最高，相比其他2种度量方式RMSE分别降低了7.6%和2.3%。然而，由于海拔、温度等环境因素影响，实际的森林蓄积量分布具有空间异质性，全局的k值在局部的森林蓄积量分布估测中可能存在局限性。Sun等[24]利用方差速率确定局部样本量构建kNN模型，实现了更合理的植被覆盖度制图。下一步将利用最优的距离度量结合局部样本量优化，确定适用于局部样本的k值对kNN进行优化，以实现更高精度的森林蓄积量估测和更合理的空间分布制图。