省域新能源与电网发展差异的时空格局演变

花秀峰，李婉莹，富丽娟，刘晶，董福贵

(1.国核电力规划设计研究院有限公司，北京100095；2.华北电力大学 经济与管理学院，北京102206)

近年来，中国新能源实现了快速发展，风电和太阳能发电稳居世界第一。到2020年底，风电累计装机281.53 GW，太阳能发电累计装机253.43 GW[1]。为实现2060年碳中和目标，新能源将超过化石能源成为主体能源[2]，风电和太阳能发电的发展前景十分广阔。但随着新能源的大量并网，新能源发电的波动性和间歇性给电网带来了巨大挑战。电网作为电力传输和电力市场的共同载体，是保障新能源发展的基本平台和主要媒介[3]。新能源和电网的协同发展是实现可持续发展的必然选择，然而各省级行政区(简称“省份”)的新能源和电网发展差异不断扩大。这种差异会影响跨区跨省的新能源消纳，最终影响中国的能源转型战略的实施。因此，研究中国新能源与电网发展差异具有重大现实意义。

针对新能源的发展，学者们多采用综合评价方法[4-5]，从经济、环境、技术和社会等多个方面对各省新能源的发展情况进行评价。文献[6]对新能源的发电效率进行评价，文献[7]研究了中国30个省份的风力发电效率及其影响因素。针对电网的发展，文献[8]从可靠性、经济性、低碳性和智能性4个维度对城市级配电网进行综合评估，文献[9]指出需要对电网进行差异化投资。对于新能源和电网发展的综合研究，多是进行综合评价[10]、效率效益评估[11]，鲜有运用空间统计分析对新能源和电网发展的时空演变进行研究。对于时空格局演变方法，马尔科夫链与空间马尔科夫链方法得到了较好的验证，已经应用在旅游业[12]、物流业[13]、区域碳排放[14-15]、农业[16]等多个领域。

综上，学者们对新能源的发展和电网发展的评价研究较多，比较分析了各省的发展差异，但忽视了邻域间的相互影响，没有同时考虑时间和空间效应对省域新能源与电网发展差异演变过程的动态研究。此外，基于新能源和电网发展的区域划分研究较少。因此，本文采用核密度估计方法、马尔科夫链与空间马尔科夫链方法，对新能源和电网发展的时空格局演变进行分析。最后，基于密度峰(density peak，DP)聚类算法对31个省份进行区域划分，为省域新能源发展提出具有针对性的建议。

1 数据来源与研究方法

1.1 研究数据

本文以中国31个省份为基本单元进行研究，由于中国新能源发电起步较晚，且省间差异较大，为保证样本的完整性和可比性，以2012—2019年各省的新能源发展和电网发展为分析指标。其中，新能源发展用风电累计装机容量和太阳能发电累计装机容量2个指标表示，数据来源于2012—2019年的国家能源局年度风电、太阳能发电并网运行情况报告[17]。电网发展用35 kV以上输电线路长度和35 kV以上变电设备容量2个指标表示，数据源于2013—2020年的《中国电力统计年鉴》[18]。此外，本文在聚类时所用的2019年新能源发电量(风电和太阳能的实际发电量之和)[17]和新能源消纳量(省内实际消纳量)[19]均来自国家能源局。

1.2 研究方法

本文以省域为空间单元，核密度估计方法可以描述新能源和电网随时间的整体演变趋势。马尔科夫链可以定量度量新能源和电网随时间格局演变的概率。空间马尔科夫链则是在马尔科夫链的基础上加入空间效应，可以分析受邻域影响的新能源和电网空间格局演变。在此基础上，DP聚类算法则结合了各省新能源和电网发展的特征，依据样本密度对区域进行划分，以便为不同区域制定具有针对性的发展建议。具体技术路线如图1所示。

1.2.1 核密度估计

核密度估计方法可以描述31个省份新能源和电网的概率密度分布情况，当对多个年份进行分析时，就可以直观地体现新能源和电网随时间的整体演变趋势。假设x1,x2,…,xN为取自新能源/电网指标总体X的N个样本，X服从同分布，且密度函数f(x)未知，需要通过样本对其密度函数进行非参数估计。标准核密度估计定义为

(1)

式中：h为计数区间宽度；n为与估计点x的距离不大于h的样本个数；xi为与估计点x距离小于h的样本点；K(*)表示核函数形式[20]。

核函数可以有多种具体形式，本文选择最常用的高斯核函数，即

(2)

核密度估计需要大量的样本数据，但本文研究的31个省份新能源和电网发展数据为小样本事件，为弥补样本信息的不足，需要采用信息扩散方法对数据进行集值化处理。最简单的信息扩散函数是正态扩散函数，一个样本点x可以将信息扩散给m个点，m个扩散点的集合用U={u1,u2,…,um}表示，每个扩散点的概率函数可表示为

(3)

式中：g(ui)为正态扩散函数；ui为第i个扩散点；ρ为扩散系数，可根据样本集合中样本的最大值和最小值及样本个数确定[21]。

样本点x扩散成m个点后，每个扩散点的核密度函数可表示为

(4)

1.2.2 空间马尔科夫链

马尔科夫链分析法可以用来计算新能源和电网随时间格局演变的概率，从而分析各省域之间不同时期的新能源和电网发展演变情况。首先将样本数据根据分位数法或等间距法划分为k个类别，然后计算各种类别的概率分布和转移情况，将其演变过程近似为马尔科夫过程。t时刻的区域类别用1×k的状态概率向量Et=(E1,t,E2,t,…,Ek,t)表示，则状态转移过程就可以用k×k的马尔科夫转移概率矩阵M抽象表示。定义pij为在t时刻中属于类别i的区域在t+1时刻转移为类别j的概率值，则

(5)

式中：nij为t时刻中属于类别i的区域在t+1时刻转移为类别j的区域数量总和；ni为实现转移的年份中属于类别i的区域数量总和。

空间马尔科夫链是传统马尔科夫链与空间自相关相结合的产物[22]。空间马尔科夫链分析法本质上是传统的马尔科夫链引入“空间滞后”概念后的产物[23]。空间马尔科夫链方法可以直观地分析受邻域影响的新能源和电网空间格局演变情况。空间马尔科夫链转移概率矩阵以某一区域a在t时刻的空间滞后类别为条件，将传统的马尔科夫链分解为k个k×k的条件转移概率矩阵。区域a的空间滞后值是该区域的空间邻近区域属性值的加权平均，即

(6)

式中：P为与区域a相邻区域的个数；B为区域总数；Wab为区域a和区域b的空间关系，邻接为1，不邻接为0；Yb为区域b的属性值；La为区域a的空间滞后值，表示区域a的邻域状态[14]。

1.2.3 DP聚类算法

Rodriguez和Laio在2014年提出了DP聚类算法，此算法是基于密度的一种聚类算法[24]。该算法能够自动地发现簇中心，实现任意形状数据的高效聚类。传统的聚类算法需要提前设定大量参数，且结果对阈值较敏感，而此算法对阈值更加鲁棒，且不需要输入聚类中心个数。DP聚类有2个准则，一是聚类中心的密度大于周边，二是不同聚类中心之间有较大的距离。可表示为：

(7)

(8)

式(7)、(8)中：dc为截断距离；dij为样本点i到样本点j的欧式距离；ρi为到样本点i的距离小于dc的点的个数；当dij-dc<0时，χ(dij-dc)=1，否则为0；δi为密度比样本点i大的所有点中与样本点i的最小距离。样本点中，ρi值小、δi值大的是异常点，两者都大的是聚类中心[25]。

2 新能源和电网发展的基本特征分析

2.1 新能源和电网发展的空间分布

虽然我国新能源发电起步较晚，但到2019年，风电并网容量达到210.05 GW，太阳能发电并网容量达到204.30 GW，均处于世界领先地位。由图1可知：风电装机量较高的地区主要集中在内蒙古、新疆、河北、陕西、甘肃和宁夏等，其中内蒙古风电装机水平遥遥领先。从整体来看，风电装机容量北方地区优于南方地区，省间差异较大。太阳能发电装机量较高的地区主要集中在山东、江苏、河北和浙江，其次为安徽、青海、陕西、内蒙古、新疆和河南；从整体来看，太阳能分布的空间集聚性较为明显，中东部沿海地区太阳能发电装机最多，省间差异相比风电较弱。

电网建设是实现新能源跨区跨省输电的基础，本文采用35 kV以上输电线路长度和35 kV以上变电设备容量2个指标来衡量各省的电网建设能力，输电线路长度代表输电距离，变电设备容量代表输电最大负荷。2019年，内蒙古、山东和河北的35 kV以上输电线路长度超过100 000 km，四川、江苏，北京、海南和上海的输电线路依次递减。2019年，江苏、广东、山东和浙江的35 kV以上变电设备容量最高，青海、海南和西藏的变电设备容量较小。图2为2019年省域新能源和电网发展空间分布情况，可以看出输电线路长度和变电设备容量的空间分布存在一定的差异：上海、浙江、福建和北京的输电线路发展弱于变电设备发展，用电密集度较高；云南、广西、新疆、甘肃、黑龙江和内蒙古输电线路发展强于变电设备发展，用电密集度较低。

图2 2019年省域新能源和电网发展空间分布

2.2 新能源和电网发展的时间序列

为了进一步了解省域新能源和电网发展的分布，选择2015—2019年数据进行核密度测算(2012—2014年大部分省份的新能源的此测算值接近0，区分效果不明显)。图3为省域新能源和电网发展的核密度测算值，由图3可知：①2015—2019年风电装机呈单峰分布，峰值有所下降，密度分布向右移动，省间差距逐渐拉大，部分省份的风电装机容量仍较小。②2015年太阳能发电装机容量普遍较低，19个省份的太阳能发电装机容量低于0.65 GW，与第20名安徽的1.21 GW出现了断层，省间发展极不平衡；2016年以后太阳能发电实现快速增长，各省之间的差距逐渐缩小；到2019年，峰值不明显，10.00 GW以下基本为均匀分布。③2015年35 kV以上输电线路长度为双峰分布，逐渐发展为2018年的单峰分布，2019年又有向双峰发展的趋势；整体来看，输电线路的建设已经较为成熟，在中间值附近的密度值较大。④35 kV以上变电设备容量则呈单峰分布，2015—2019年峰值在不断波动，密度函数在缓慢地向右移动，省域间仍存在较大差距。

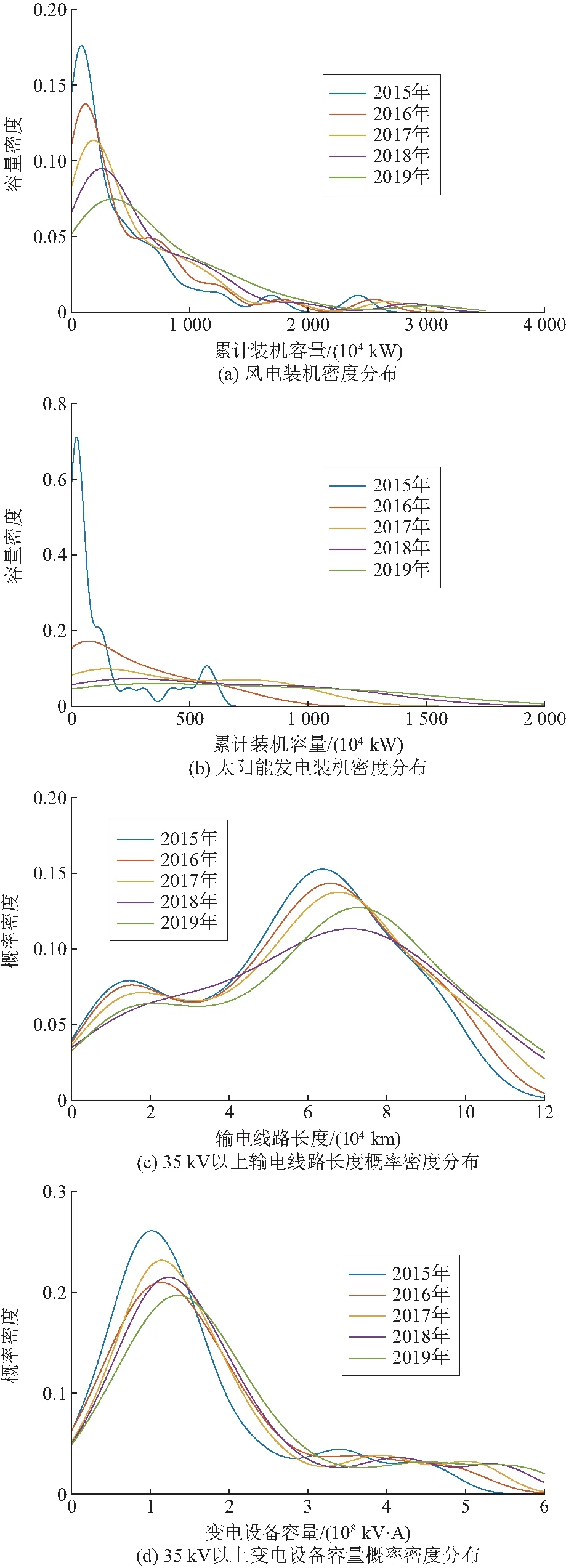
图3 省域新能源和电网发展的核密度测算值

3 新能源和电网发展差异的时空格局演变

本文采用等间距法将样本数据划分为4个类别，分别为Ⅰ(<33%，表示小于样本均值的33%，下同)、Ⅱ(33.3%～100%)、Ⅲ(100%～166.6%)、Ⅳ(>166.6%)。类别Ⅰ为发展最弱，类别Ⅱ为发展较弱，类别Ⅲ为发展较强，类别Ⅳ为发展最强。利用马尔科夫链和空间马尔科夫链对省域新能源和电网发展类别的转移进行分析，由弱到强为类别上升，由强到弱为类别下降，具体分析见3.1、3.2节。

3.1 新能源和电网发展差异的时间格局演变

利用马尔科夫链分析，分别得到2013—2019年各省新能源和电网发展类别的马尔科夫转移概率矩阵，见表1。

表1 2013—2019年省域新能源和电网发展类别的马尔科夫转移概率矩阵

从表1可以看出：①对角线上的概率值均大于非对角线的概率值，类别不变的可能性更大，风电装机保持原有类别的概率至少为75.9%，太阳能发电装机保持原有类别的概率至少为61.9%，输电线路长度保持原有类别的概率至少为80.0%，变电设备容量保持原有类别的概率至少为85.7%；②各类别之间的转移概率均较小，风电装机发生类别转移的可能性最大为13.8%，太阳能发电装机发生类别转移的可能性最大为19.6%，输电线路长度发生类别转移的可能性最大为18.0%，变电设备容量发生类别转移的可能性最大为11.9%；③在4个矩阵中，太阳能发电装机类别变动的概率最大，其次为风电装机类别，且上升概率大于下降概率，说明部分省份的新能源发展仍有较大潜力；④风电装机、太阳能发电装机和变电设备容量类别Ⅳ的稳定性最好，输电线路长度类别Ⅲ的稳定性最好，整体上两边类别的稳定性优于中间类别；⑤转移多发生在邻近类别之间，仅太阳能发电装机存在由类别Ⅰ上升为类别Ⅲ、类别Ⅱ上升为类别Ⅲ的可能性，最大值为仅4.3%。

3.2 新能源和电网发展差异的空间格局演变

根据2013—2019年各省的新能源和电网发展类别，利用ArcGIS软件对新能源和电网发展空间类别格局演变进行绘图。在传统的马尔科夫转移概率矩阵的基础上加入邻域类别为条件，辨别不同邻域类别对城市碳排放强度类别转移的影响，并对邻域类别的转移情况进行空间可视化。具体如图4所示。

由图4可知，2013—2019年，各省域新能源发展类别的变动较大，电网发展类别的变动则较小。其中，14个省份的风电装机类别上升(例如由类别Ⅰ上升为类别Ⅱ)，3个省份的风电装机类别下降(例如由类别Ⅳ下降为类别Ⅲ)，南部地区风电实现快速发展，类别下降的省份集中在东北地区。13个省份的太阳能发电装机类别上升，8个省份的太阳能发电装机类别下降，东北地区和河南及其周边省份的太阳能发电迅速发展，内蒙古、宁夏和甘肃的太阳能发电装机类别由类别Ⅳ下降为类别Ⅲ。整体来看新能源的发展，大部分省份均发生了转移，新能源发展的空间格局变动较大，安徽、贵州、河南、湖南、陕西和云南的风电装机和太阳能发电装机均实现向上转移。26个省份的输电线路长度类别未发生改变，类别上升的有西藏和内蒙古，类别下降的有黑龙江、江苏和陕西。26个省份的变电设备容量类别未发生改变，类别上升的有安徽和内蒙古，类别下降的有湖北、山西和上海。整体来看电网的发展，大部分省份均未发生转移，说明电网的发展相对稳定，内蒙古地区的输电线路长度和变电设备容量均实现向上转移。安徽和陕西新能源的发展对电网发展具有积极促进作用。

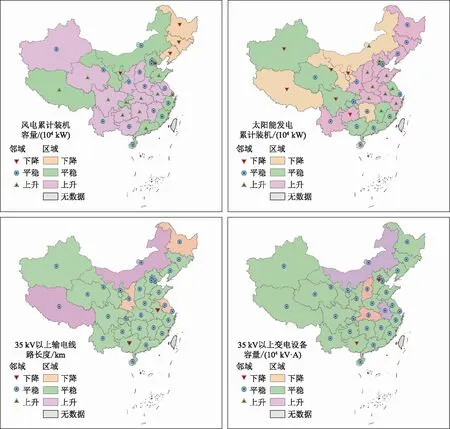
图4 2013—2019年省域新能源和电网发展及邻域类别转移的空间分布格局

本区域和邻域风电装机同时向上转移的省份有安徽、贵州、湖北、湖南、青海和四川，各省呈“V”字相邻排列，同时向下转移的省份集中在东北地区，风电装机受区域背景的影响较大。本区域和邻域太阳能发电装机同时向上转移的省份有安徽、河北、河南、湖北、山东、山西和浙江，各省相邻，同时向下转移的省份有甘肃、宁夏、西藏，太阳能发电装机受区域背景的影响较大。输电线路长度和邻域输电线路长度类别同时向上变化和向下变化的空间分布不一致，变电设备容量也是如此，说明电网发展受区域背景的影响较小。综上，新能源发展的空间趋同变化较电网发展的空间趋同变化更明显。

4 区域划分

采用DP聚类算法对各省新能源发展和电网发展分别聚类。考虑到新能源的实际消纳情况，本文将风电累计装机容量、太阳能发电累计装机容量和新能源发电量作为聚类指标对新能源发展进行聚类，将35 kV以上输电线路长度、35 kV以上变电设备容量和新能源消纳量作为聚类指标对电网发展进行聚类。先对各指标进行无量纲化处理(实际值除以指标最大值)，再对新能源发展和电网发展分别进行DP聚类，聚类结果见表2。

最终，新能源发展分为3类，第1类的省份数量最多，有18个省份(对应表2中新能源发展分类为1的整行省份，下同)，第3类仅有内蒙古，由第1类到第3类新能源发展逐渐增强；电网发展分为3类，第1类的省份数量偏多(对应表2中电网发展分类为1的整列省份，下同)，第2类省份的数量其次，整体比较均匀，由第1类到第3类电网发展逐渐增强。具体聚类中心见表3。

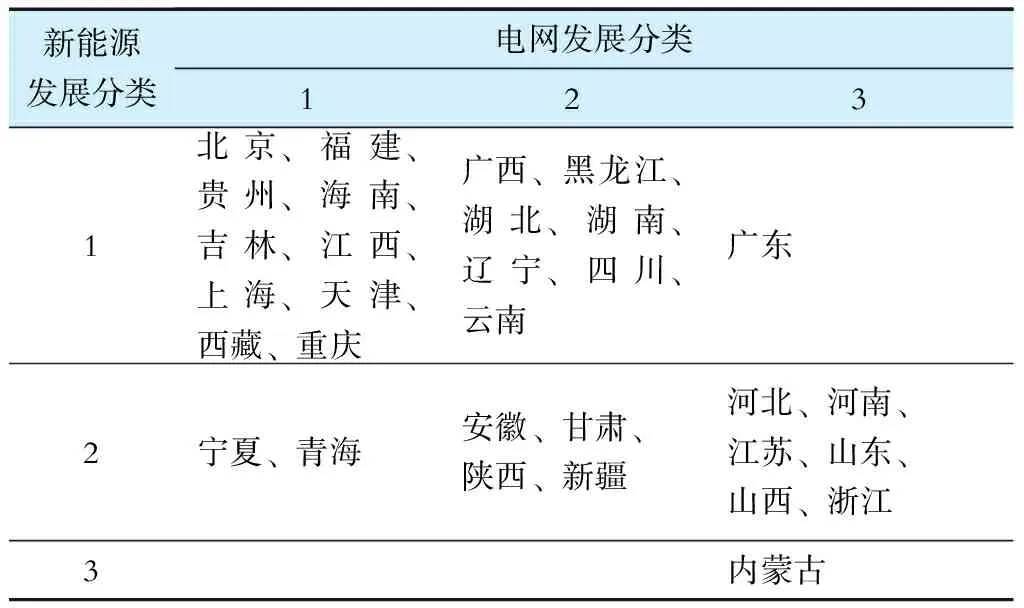
表2 区域划分结果

整理DP聚类结果，得到如表3所示的区域划分结果。位于(1，1)的有10个省份，位于(2，2)的有4个省份，位于(3，3)的有1个省份，共计15个省份，新能源和电网的发展水平相当，在今后的电力发展中，应注重新能源和电网的同步发展。位于(1，2)的有7个省份，位于(2，3)的有6个省份，共计13个省份，新能源发展弱于电网发展，在今后的电力发展中，应优先发展新能源。位于(1，3)的有1个省份，新能源发展远弱于电网发展，在今后的电力发展中，应重点发展新能源。位于(2，1)的有2个省份，新能源发展强于电网发展，在今后的电力发展中，应优先发展电网。(3，1)、(3，2)对应坐标无省份。

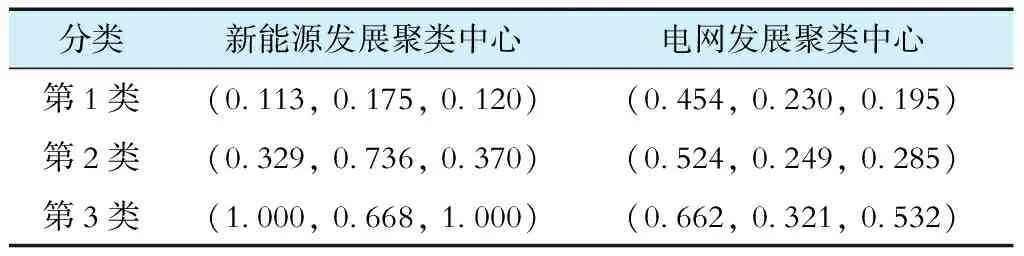
表3 DP聚类结果

5 结论

本文采用核密度估计方法，对新能源和电网发展的基本特征进行分析。基于马尔科夫链与空间马尔科夫链的方法对新能源和电网发展的时空格局演变进行分析，并采用DP聚类算法对31个省份进行区域划分。研究得出以下结论：

a)风电装机容量北方地区优于南方地区，太阳能分布的空间集聚性较为明显，中东部沿海地区太阳能发电装机容量最多。上海、浙江、福建和北京的输电线路发展弱于变电设备发展，用电密集度较高；云南、广西、新疆、甘肃、黑龙江和内蒙古输电线路发展强于变电设备发展，用电密集度较低。

b)2015—2019年风电装机容量呈单峰分布，峰值有所下降，密度分布向右移动，省间差距逐渐拉大；2015年太阳能发电装机容量普遍较低，到2019年，峰值不明显，10.00 GW以下基本为均匀分布。2015年的输电线路长度为双峰分布，逐渐发展为2018年的单峰分布；2015—2019年变电设备容量峰值在不断波动，密度函数在缓慢地向右移动。

c)通过马尔科夫链分析可知，各类别之间的转移概率均较小，在4个指标矩阵中，太阳能发电装机类别变动的概率最大，其次为风电装机类别，且类别上升概率大于类别下降概率，说明部分省份的新能源发展仍有较大潜力。

d)通过空间马尔科夫链分析可知，新能源发展的空间格局变动较大，电网的发展相对稳定，安徽和陕西新能源的发展对电网发展具有积极促进作用。新能源发展的空间趋同变化较电网发展的空间趋同变化更明显。

采用DP聚类算法对省域新能源发展和电网发展分别聚类，最终将31个省份划分为7类，根据新能源和电网的发展特点，提出具有针对性的新能源和电网发展建议。