基于多层迭代算法的电网检修计划优化方法
凌亮,何强,熊正勇,赖晓文,李思思,张丙金
(1.国家电网有限公司西南分部,四川 成都 610041;2.北京清能互联科技有限公司,北京100084)
电力设备是电网的重要组成部分,在其日常运行过程中,可能会随着运行时间的推移出现各种故障。为避免在电力系统正常运行时因电力设备发生故障引发电网安全问题,需要在对电力设备进行检修之前制订合理科学的检修计划[1]。
制订检修计划是电网调度部门的重要业务,近年来,电网运行管理精益化的要求不断提高,这不仅要求检修计划满足电网运行的安全性需求,还要能够合理安排电力设备的检修时间,避免重复检修和检修冲突等问题,从而降低设备检修对用户带来的用电影响[2-4]。为此,针对电力设备检修计划的研究成为电网调度智能化发展的重点之一。
目前,我国对电网检修计划智能编排的研究相对较少,尚处于起步阶段[5]。传统电网检修计划根据人工经验进行编排,较为粗放,得到的计划可行性欠佳,亟需对电网检修计划的智能编排进行深入研究。文献[6-8]针对含复杂约束的发输电检修计划优化问题,提出使用Benders分解法将检修计划优化问题分解为一个主问题和若干个子问题进行求解;文献[9-10]采用动态规划法对通过建立决策树获得的配电网检修计划方案进行比较,以得到最佳检修计划方案;文献[11-13]应用遗传算法分别对最优检修停电决策问题、梯级水电站中长期调度和检修计划双层优化模型,以及输电系统检修计划优化模型进行求解;文献[14-15]采用粒子群算法,分别对配电网设备检修计划联合设备位置自动切换优化模型,以及考虑电网运行总风险和设备检修收益联合的检修计划优化模型进行求解;文献[16]使用一种将混沌粒子群分层算法和改进的旅行商问题(traveling salesman problem,TSP)搜索算法结合的混合算法,求解含光伏-储能联合发电系统和可控负荷的配电网双层检修计划优化模型;文献[17-19]利用混合整数规划法分别求解水电系统发电机检修计划优化模型、含有大规模可再生能源接入的输电设备检修计划模型、电力市场下的发电检修计划协调优化模型,以及机组发电调度和检修计划联合优化模型。
上述文献求解电网检修计划优化模型的方法主要包括Benders分解法、动态规划法、各种智能算法和混合整数规划法。Benders分解法的优势是其能够巧妙缩减模型规模,不断缩小优化问题的解空间,提高模型求解的计算效率,但是其在决策变量数量达到一定规模时,仍存在计算效率低下的问题;动态规划法具有方法灵活、原理直观等优点,特别适用于离散型问题的求解,但是其缺点在于较难考虑复杂的约束条件,当优化问题的规模较大时,易出现“维数灾”,且无法保证求解效率;智能算法的基本原理是模仿某些自然现象以求解优化问题,这类算法易陷入局部最优解,不能保证得到全局最优解,并且稳定性和鲁棒性不足是其致命缺点,难以适用于求解大规模实际工程问题;混合整数规划法求解混合整数优化问题的方法为分支割平面法,该方法结合了分支定界法和割平面法,是许多商业优化软件的核心算法,但是当模型的规模较大,尤其是整数变量较多时,模型求解难度呈指数级增加,无法有效解决计算效率低下的问题。综上分析,电网检修计划优化问题是大规模混合整数规划问题,采用上述算法进行求解仍然存在计算效率低、收敛性差等问题。
为此,本文提出一种多层迭代的混合整数规划算法,用于求解大规模检修计划优化模型。首先建立电网年检修计划优化模型,该模型的目标为检修计划编排总数最大,决策变量包括检修计划总状态、检修开始时间和检修计划日状态,约束条件包括日检修数量限制约束、检修同时约束、检修互斥约束等。其次采用多层迭代算法对模型求解,由于检修计划要求尽可能按照上报检修日期进行安排,第1层计算按照将检修开始时间取值范围不断放宽的思路进行多次迭代计算,直到检修开始时间的取值范围大于0到总检修周期;若第1层计算结束后仍有检修计划未被优化,则进行第2层计算,这层计算将日检修最大数设为日检修数平均值,然后进行多次迭代计算,计算逻辑与第1层计算相同;第2层计算结束后,若还有检修计划未被安排,则考虑对日检修最大数进行松弛,重复多次迭代计算,直到检修计划被全部成功安排。最后,基于某省级电网,验证本文所提优化算法的正确性和可行性。
1 检修计划优化模型
本文对检修计划的优化即对需要检修的设备在相应检修项目中的检修时间进行优化。
1.1 目标函数
检修计划优化模型以尽可能满足检修计划需求为目标,即
(1)
式中:N为检修计划总数;αi为第i条检修计划的总状态,为0-1变量,1表示执行,0表示不执行。
1.2 约束条件
检修计划优化模型的约束条件主要包括检修计划总状态、检修开始时间和检修计划日状态变量之间的耦合约束、检修窗口期约束、日检修数量限制约束、检修同时约束、检修互斥约束、检修时序约束、重复停电约束、一停多用约束以及区域保电约束。并且上述检修窗口期、检修同时、检修互斥和区域保电等停电规则,是电网调度员为了考虑电网安全、稳定运行而制订的,因此本文所提检修计划优化模型中并未直接涉及电网安全约束。
1.2.1 决策变量之间的耦合约束
a)检修开始时间与检修计划总状态之间的耦合约束
αi≤xi≤αiT.
(2)
式中:xi为第i条检修计划的检修开始时间,为整数变量;T为总检修周期,1年为365 d。式(2)表示当执行第i条检修计划时,其检修开始时间的取值范围为[0,T];若不执行时,则检修开始时间为0。
b)检修开始时间与检修计划日状态之间的耦合约束
(3)
式中:yi,t为第i条检修计划在第t日的检修状态,为0-1变量,0表示不检修,1表示检修;Ti为第i条检修计划的检修工期。式(3)表示第i条检修计划在其检修区间xi≤t≤xi+Ti-1内处于检修状态,在检修区间外检修状态为0。但是,式(3)为非线性约束,需要对其进行线性化处理,具体转化过程如下。
由逆否定理可得:
(4)
引入检修计划日状态辅助0-1变量zi,t,将式(4)转化为
(5)
由式(5)可知:当yi,t=1时,式(5)恒成立,不构成约束;当yi,t=0时,xi≥t+1‖xi≤t-Ti必有一个成立,取决于zi,t的值,当zi,t=0时xi≥t+1,当zi,t=1时xi≤t-Ti。
同理可得:
(6)
将式(6)线性化为
T(yi,t-1)≤t-xi≤Ti-1+(T-Ti+1)(1-yi,t).
(7)
由式(7)可知:当yi,t=0时,式(7)恒成立,不构成约束;当yi,t=1时,xi≤t≤xi+T-1成立。
1.2.2 检修窗口期约束
检修窗口期表示设备只能安排在其检修窗口期内进行检修,约束如下:
yi,t=0,t∉Ωi,win.
(8)
式中Ωi,win为第i条检修计划的检修窗口期集合。
1.2.3 日检修数量限制约束
考虑电网安全和电网承载力,需要限制每日检修设备数,以保证电网的正常稳定运行。
(9)
式中Dt为第t日检修最大数。
1.2.4 检修同时约束
为避免重复停电,有些检修设备需要满足同时检修的要求,约束为:
(10)
式中:Ωi为同时检修计划集合;M为同时检修计划集合中的检修计划数量。
1.2.5 检修互斥约束和重复停电约束
某些检修设备同时停电会导致其他设备出现过负荷情况,因此需要满足互斥约束,即
yi∈s1,t+yi∈s2,t≤1s1,s2∈Ωj
(11)
式中Ωj为不同时检修集合;检修设备s1和s2属于检修互斥集合Ωj。
同一设备可能对应多条检修计划,若该设备需要进行多次检修,则这些检修计划必须分开执行,并且满足重复停电约束,其建模方式与检修互斥约束相同。
yi1,ta+yi2,ta≤1,i1,i2∈Ωa.
(12)
式中:Ωa为设备a对应的检修计划集合;yi1,ta为设备a的检修计划i1在第t日的检修状态,yi2,ta为设备a的检修计划i2在第t日的检修状态。
1.2.6 检修时序约束
特定检修项目会设置前序项目,且设有时间间隔,例如计划j的检修开始时间必须在计划i的结束时间之后,且只有计划i检修结束满足一定时间间隔后,计划j才能执行。
(13)
式中Wj为计划i检修结束时间与计划j检修开始时间之间的时间间隔。
1.2.7 “一停多用”约束
同一设备可能对应多条检修计划,没有要求这些计划一定要分开执行,为了提高检修效率,避免重复检修,将这些计划规定在同一时间内进行检修。
xi,a=xj,a,i,j∈Ωa.
(14)
1.2.8 区域保电约束
若某区域要求在节假日或特殊会议期间不能停电,则该区域下的设备在这些指定期间内不能进行检修操作。
(15)

2 模型求解
本文建立的检修计划优化模型为整数规划,由式(1)、(2)、(5)、(7)—(15)组成。由于模型中整数变量“检修开始时间”的取值范围过宽,并且模型存在大量的0-1变量,使得解的可行域空间过大,造成模型求解效率非常低,采用CPLEX软件难以在短时间内找到可行解。
为解决检修计划优化模型求解困难问题,本文提出多层分步迭代计算的方法对模型进行求解,求解流程如图1所示。
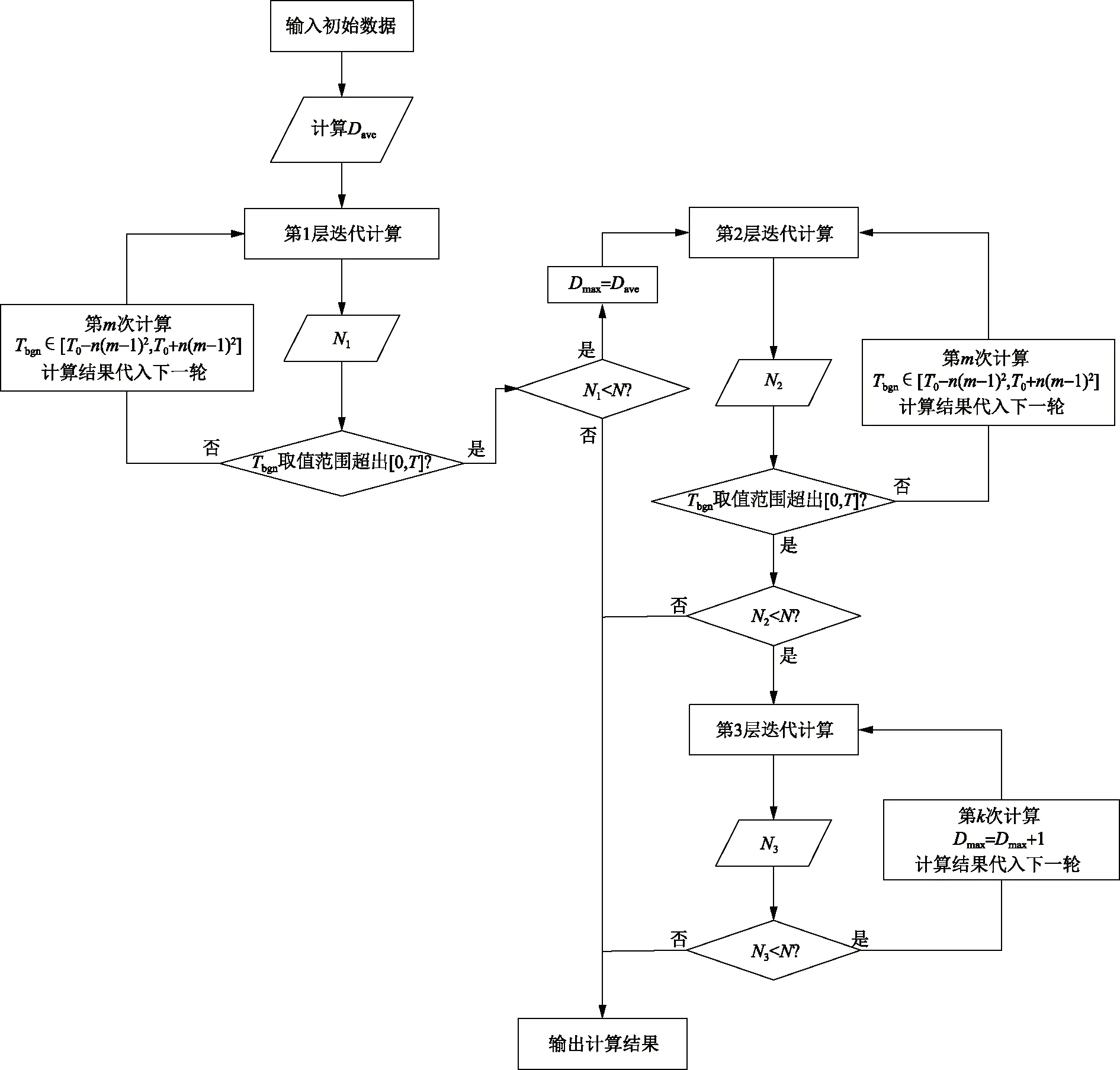
图1 检修计划优化模型求解流程
a)输入初始数据,包括检修计划申报日期(开始时间和结束时间)、检修计划窗口期、日检修最大数等,根据检修计划申报开始时间和结束时间,以及总检修周期计算日检修平均数Dave。
b)开始第1层迭代计算,按照将检修开始时间Tbgn的取值范围不断放宽的思路,调用CPLEX软件采用分支切割算法(branch-and-cut)对模型进行多次迭代求解。第1次计算将所有检修计划的检修开始时间设为申报开始时间T0,第2次计算将检修开始时间取值放宽为[T0-n,T0+n],第3次计算放宽为[T0-n×22,T0+n×22],第m次计算放宽[T0-n(m-1)2,T0+n(m-1)2],若T0-n(m-1)2≤0,取T0-n(m-1)2=0;若T0-n(m-1)2≥T,取T0-n(m-1)2=T,直到检修开始时间的取值范围超出[0,T],迭代计算终止。将每次优化的检修计划固定下来,没有优化的检修计划在下一次计算中放宽约束继续优化,每次优化的检修计划总数量为N1。另外,参数n决定了计算次数及每次计算的取值宽度,如果取值太大,计算次数减少,但是计算效率及收敛性会受到影响;取值太小,虽然收敛性会提高,但是计算次数会增加,同样会影响到计算效率,并且可能会降低解的质量,因此应根据实际情况合理设置参数n。
c)若第1层迭代计算完毕后,仍有检修计划未被优化,则进行第2层迭代计算。为达到每日检修数均衡的目的,将日检修最大限制数设为日检修平均值,使得每日检修数逼近日检修平均值。计算逻辑与第1层迭代计算相同,每次计算后被成功安排下来的检修计划总数为N2。
d)若第2层计算完成后,仍有检修计划未被优化,则进行第3层计算。同样为使得每日检修数均衡,该层计算每次对日检修最大数松弛1个数,直到所有检修计划被成功安排为止。N3为第3层迭代计算中每次计算后被成功安排的检修计划总数。
3 算例分析
以某省级电网为例,验证本文所提检修计划优化方法的有效性。申报的检修计划总共180条,其中有141台检修设备和94个检修项目,检修起始日期为2021年1月5日,终止日期为2021年12月18日,总检修周期348 d。
采用本文提出的多层迭代算法对上述180条检修计划进行优化,经测试,算法能够在满足所有约束条件的情况下成功对所有检修计划进行优化,优化计算时间为376 s。下面对优化结果进行分析。
3.1 优化结果分析
3.1.1 检修窗口期规则分析
本测试算例对设备87设置了检修窗口期,为2021年2月5日—2021年7月2日,其对应检修计划优化后的检修时间为2021年4月6日—2021年4月9日,在其检修窗口期内,见表1。

表1 设备87对应检修计划优化后的检修时间
3.1.2 检修同时规则分析
本测试算例包括1个同时检修计划集合,集合中包含设备68和设备71,2个设备对应检修计划的检修时间优化结果见表2。

表2 检修同时计划优化结果
3.1.3 检修互斥规则分析
本测试算例包括1个检修互斥集合,集合中包含设备49和设备90,2个设备对应检修计划的检修时间优化结果见表3。
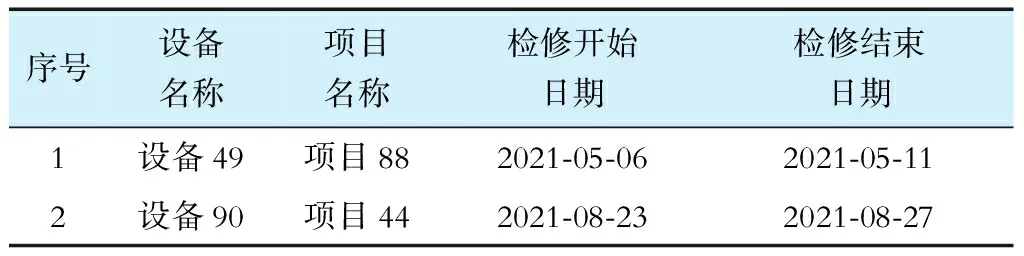
表3 检修互斥计划优化结果
3.1.4 检修时序规则分析
本测试算例包括1个检修时序集合,集合中包含项目48和项目49,且规定项目48在结束10天后才能实施项目49,2个项目对应检修计划的检修时间优化结果见表4。
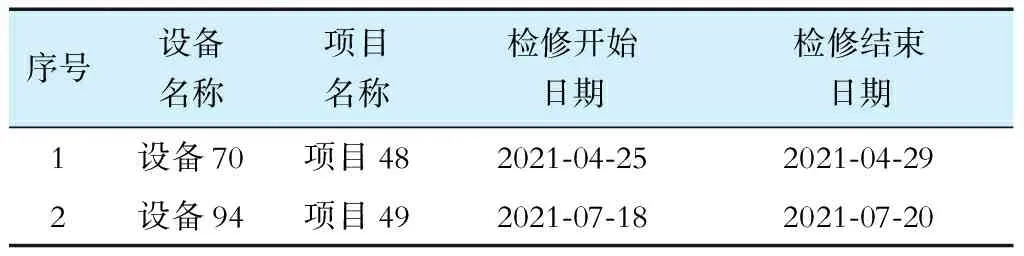
表4 检修时序计划优化结果
3.1.5 不可调整规则分析
本算例含有2条不可调整检修计划,其检修时间必须与申报时间一致,见表5。

表5 不可调整检修计划优化结果
3.1.6 重复停电规则分析
以设备118为例进行分析,该设备对应可重复停电检修计划的优化结果见表6。从表6可以看出,各条计划的检修时间均不一样且不交叉,严格遵守分开执行的规则。

表6 可重复停电检修计划优化结果
3.1.7 “一停多用”规则分析
同样以设备118为例,该设备对应的不可重复停电检修计划的优化结果见表7。由表7可知,各条计划的检修开始时间均相同,相当于合并成了一条计划,实现“一停多用”。

表7 不可重复停电检修计划优化结果
3.1.8 区域保电规则分析
本算例对区域1进行保电设置,设置该区域的保电区间为2021年7月1日—2021年7月30日,该区域下所有设备对应的检修计划均未在保电区间内进行停电检修,见表8。

表8 区域1下设备对应检修计划优化结果
3.1.9 检修编排均衡性分析
检修编排均衡性可通过每日设备检修数量来体现,本算例的每日设备检修数量优化结果如图2所示。从图2可以看出,每日设备检修数量均集中在2~4之间,均衡性很好。

图2 每日设备检修数量分布
3.1.10 优化时间与申报时间偏差分析
经本文算法优化后,所有检修计划均被成功安排。其中,87条计划按照申报时间进行检修,占比48.3%;申报时间与优化时间不相同且相差10 d内的检修计划包含23条;申报时间与优化时间相差大于10 d且在30 d内的检修计划包含19条;申报时间与优化时间相差大于30 d且在90 d内的检修计划包含27条;申报时间与优化时间相差大于90 d且在180 d内的检修计划包含18条;申报时间与优化时间相差大于180 d的检修计划只有6条。
3.2 算法优越性验证
为验证本文所提方法的优越性,使用CPLEX软件直接对整个模型进行一次性求解,分别采用分支切割算法和动态搜索算法(dynamic search),其求解结果与本文优化结果的对比如表9和图3所示。表9为本文求解方法和一次性求解方法的求解效率对比情况。

表9 求解效率对比
可以看出,采用分支切割和动态搜索算法计算耗时分别是3 603 s和4 017 s,总共有178条检修计划被成功优化,还有2条计划未被安排,这表明采用一次性求解方法直接求解原问题,计算效率均较低,而本文所提算法的计算效率高,优化效果更好。图3为本文求解方法与一次性求解方法的每日设备检修数量优化结果对比情况,由图3可见采用本文算法对检修计划进行优化更有利于检修编排的均衡性。

图3 本文求解方法与一次性求解方法的每日设备检修数量对比情况
为进一步体现本文算法的鲁棒性和稳定性,将电网规模增大到含有272条检修计划和953条检修计划,分别称为模型272和模型953。分别采用本文求解方法和一次性求解(分支切割)方法求解,结果见表10。

表10 本文方法和一次性方法(分支切割)求解模型272和模型953的效率对比
由表10可知,采用本文方法求解模型272和模型953的计算时间分别为1 531 s和3 022 s,并且能够成功优化所有检修计划,而采用一次性方法求解,计算时间长达36 005 s和36 062 s,均达到10 h,优化效果不佳,尤其当电网规模增加,其优化效果更差,模型953的优化比例只有62%。这说明随着电网规模增大,本文提出的优化算法计算时间有所增加,能够成功安排所有检修计划。
4 结束语
本文提出一种基于多层迭代算法的电网检修计划优化方法。首先,建立以尽可能多地安排检修计划为目标的年度检修计划优化模型,为使得该模型能够满足检修业务的要求,以检修开始时间、检修计划总状态和检修计划日状态为决策变量,采用线性化技术对三者的耦合关系建模,并利用3个决策变量对检修业务相关的所有约束条件建模,很好地解决了整个检修计划优化的数学建模问题。其次,由于本文建立的检修计划优化模型为大规模整数规划问题,采用传统算法不能有效求解,本文采用多层迭代的计算方式对其进行求解。最后,某省级电网算例结果表明,本文所提检修计划优化方法不仅可以成功安排所有检修计划,还可以满足每日检修设备编排的均衡性。

