基于多任务学习的公路隧道支护方案优化分析
渠成堃,吴德兴,李伟平,张传庆
(1.浙江省交通规划设计研究院有限公司,杭州 310030;2.水下隧道智能设计、建造及养护技术与装备交通运输行业研发中心, 杭州 310030;3.中国科学院武汉岩土力学研究所,武汉 430071)
近年来,随着中国交通基础设施的发展,隧道建设规模越来越大[1-2]。现场隧洞掘进过程中地质条件频繁变化,设计提供的支护方案越来越难持续适应后续复杂的地质条件。而在隧道支护设计时,支护方案多为定制化方案,难以根据围岩特征变化做出针对性的响应,且针对现场不同的地质条件定制化方案可能会造成不必要的材料浪费。
为制定更有效、更具针对性的支护方案,姬海[3]分析了不同围岩分级标准后,基于岩体质量分级(rock mass rating,RMR)方法确定了一种长短锚杆结合、强钢架的支护方式。童建军[4]针对围岩分级指标跨度较大的情况,进一步划分了亚级,并结合数值计算方法研究了各亚级围岩的隧道支护参数。大量研究人员针对公路、铁路隧道支护方案的分析总结,对中国公路隧道建设具有深刻的指导意义。
随着人工智能技术发展,大量学者将智能算法应用于公路隧道建设中[5-8]。朱利明等[9]通过遗传算法进行支护优化设计,确定成本与安全性间的平衡点。夏永旭[10]利用BP(back propagation)神经网络算法实现围岩等级预测,并选择了相应的支护方案。杨卓等[11]通过BP神经网络进行了岩溶隧道突水预测。焦战等[12]提出了基于博弈组合赋权和综合灰色关联分析的支护参数优选方法,通过工程案例证明了其可行性,对类似隧道工程提供了参考和借鉴。姚添智等[13]采用BP神经网络训练了地下厂房系统锚杆支护的智能化设计模型。
人工智能技术一定程度上促进了支护设计的发展,但支护设计的实时性没有明显提高,部分支护方法的泛化能力较弱,并且无合理的方式评估模型预测和实际方案。为此,现以溧阳至宁德高速公路(G4012)浙江景宁至文成段龙丽温隧道为背景,对围岩特征数据清洗后,关联相关支护参数,计算获得围岩特征与支护参数的相关性。进一步构建基于深度学习的多任务算法模型,开展支护方案动态优化。最终通过层次分析法对比不同支护方案,确定最合理支护方案。
1 地质与支护特征相关性分析
1.1 隧道工程概况
溧阳至宁德高速公路浙江景宁至文成段属于浙江省“十二五”交通建设规划“两纵两横十八连三绕三通道”中的一连——龙(游)丽(水)温(州)高速公路的一部分。区内出露前第四纪地层主要有下白垩统(K1)火山岩、陆相碎屑沉积岩及侵入岩。第四纪地层主要为冲洪、坡洪积的砂砾石层和砂性土和黏性土层等。
根据松散岩类地下水的赋存条件分析,勘察区内主要为松散岩类孔隙潜水和基岩裂隙水。地下水赋存相对较为贫乏,对支护设计影响较小。
1.2 地质特征与支护特征处理
为保证研究成果能够指导后期工程,本研究仅选取以往《项目现场办公记录》中可获得的围岩地质特征及相应的支护类型编号进行模型训练。
基于《公路隧道设计规范》[14]和修正的岩体分级质量指标(basic quality,BQ)值围岩判别标准中的围岩特征分析,在挖掘现场办公记录后发现主结构面倾角、地应力特征无明显描述。岩性为名称类特征,其作用仅在于结合围岩风化特征确定围岩强度情况。因此初步确定围岩风化程度、坚硬程度、岩体完整程度、地下水状态、围岩稳定情况作为输入围岩特征,如表1所示。

表1 围岩特征与支护参数Table 1 The surrounding rock features and support parameters
进一步获得不同围岩特征下的支护参数明细,见表2。在分析支护参数后认为,本项目不同围岩特征对于超前支护方式、二次衬砌参数的影响较小。因此,进一步确定本次分析预测支护参数为:锚杆间排距、锚杆长度、喷砼厚度、钢拱架类型。
1.3 地质特征与支护特征相关性分析
为进一步分析不同特征相关性,对文字性特征进行数字化映射。将围岩特征按照优势程度,从小到大进行特征数字化表征。围岩风化程度划分为5级,那么未风化定义为0,微风化为1,中风化为2,强风化为3,全风化为4。坚硬程度划分5级,坚硬岩对应为0,较坚硬岩为1,较软岩为2,软岩为3,极软岩为4。岩体完整程度分为5级,完整对应为0,较完整为1,较破碎为2,破碎为3,极破碎为4。地下水状态分为4级,其中“无水”状态为0,“潮湿或滴水”为1,“淋雨状或涌流状出水,水压<0.1 MPa或单位出水量<10 L/(min·m)”为2,“淋雨状或涌流状出水,水压>0.1 MPa或单位出水量>10 L/(min·m)”状态为3。
同理,锚杆间排距划分为6个等级,间排距“必要时”为0级,“1.5 m×1.5 m”为1,“1.2 m×1.5 m”为2,“1.2 m×1.2 m”为3,“1.0 m×1.2 m”为4,“0.75 m×1.0 m”为5。锚杆长度划分4个等级,2 m为0级,2.5 m为1级,3 m为2级,3.5 m为3级。喷砼厚度划分5个等级,6 cm为0级,10 cm为1级,18 cm为2级,20 cm为3级,25 cm为4级。钢拱架型号划分3级,无拱架为0级,格栅钢拱架为1级,14号工字钢拱架为2级。通过数字化表征得到与表2支护参数相应的数字特征,见表3。

表2 围岩特征对应支护参数Table 2 Support parameters corresponding to surrounding rock features
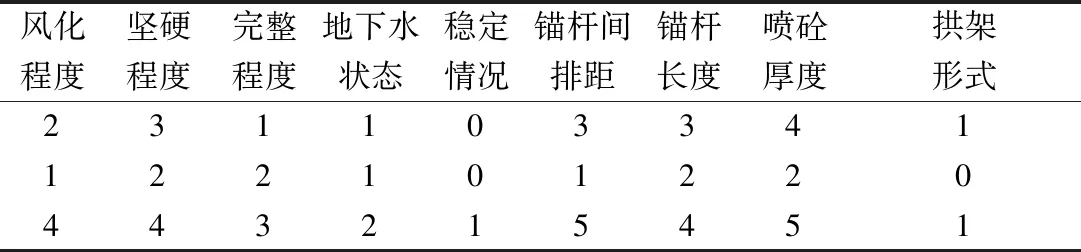
表3 围岩特征对应支护参数特征表Table 3 Support parameters corresponding to surrounding rock features
进一步通过Python分析特征相关性[15],Python分析特征相关性的指标主要有:Pearson相关系数、Kendall相关系数、Spearman相关系数。其中,Spearman相关系数引入了“秩次”概念,即n个样本按照特征1排列时,相应特征2在其正确排序中的次序,并引入参数d代表特征1“秩次”与特征2“秩次”差的绝对值。显然,如果两特征没有相同“秩次”,则相关系数可以表示为
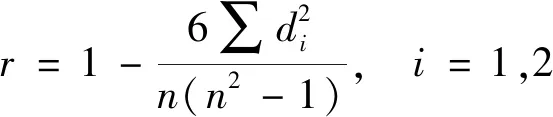
(1)
若两特征“秩次”相同,则显然d≡0,这时需要通过Pearson相关系数公式来计算系数,即
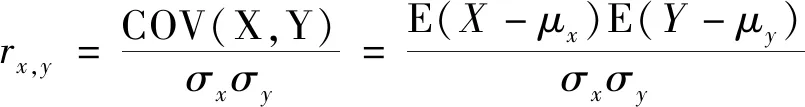
(2)
式(2)中:X、Y分别代表相关的两个特征;μx、μy分别代表特征X、Y的数学期望;σx、σy分别为X、Y的标准差。
Spearman相关系数常被称为非参数相关系数,这是因为只要两特征具有单调的函数关系,就是完全Spearman相关的。Spearman相关性不仅考虑了Kendall相关中的“秩次”,同时也结合了Pearson相关系数的计算公式。因此后续分析中选用Spearman相关性系数判断特征相关性。
表4中围岩特征与支护参数间的相关性系数,反应了不同围岩特征下支护参数的变化敏感程度。基于围岩特征变化情况,对不同支护特征响应围岩特征变化的敏感程度排序,结果如下。
(1)风化程度:锚杆间排距≈喷砼厚度>锚杆长度>拱架形式。
(2)坚硬程度:锚杆间排距>喷砼厚度>锚杆长度>拱架形式。
(3)完整程度:锚杆间排距>喷砼厚度>拱架形式>锚杆长度。
(4)地下水状态:锚杆长度>锚杆间排距≈喷砼厚度>拱架形式。
(5)稳定程度:拱架形式>锚杆长度>锚杆间排距≈喷砼厚度。
(6)另外从表4的相关系数值来看,支护特征随风化程度的变化更为频繁,其次为稳定情况、完整程度、坚硬程度。本次研究中地下水状态与支护参数并没有呈现出明显的相关关系,主要原因在于项目地下水状态较为单一,集中在无水或滴水情况,对支护参数影响较小。
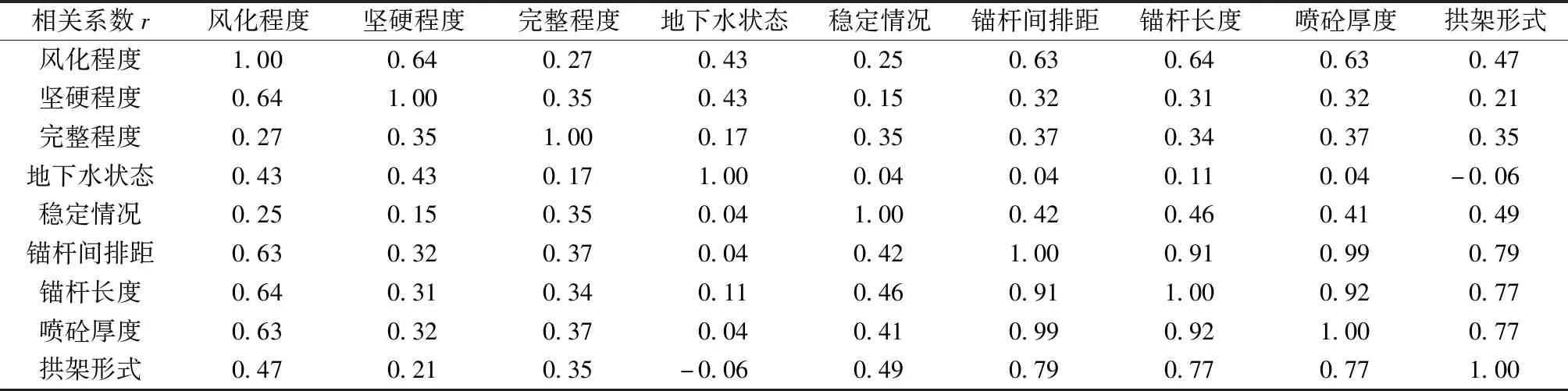
表4 不同特征Spearman相关系数表Table 4 Spearman correlation coefficient of different features
2 多任务学习的支护模型
2.1 多任务学习模型设计
通常大多数深度学习模型均为独立学习,即所谓的单任务学习(single-task learning,STL),模型仅针对一个特定任务,预测一类回归或分类问题的结果,例如通过一张岩石图片识别岩性。
通常为了优化模型预测效果,需构建目标函数评估并提升模型效果。目标函数通常由表征预测值与真实值之间误差的经验损失和描述模型复杂程度的正则项J(又称为“结构化损失”)[9]构成,表示为
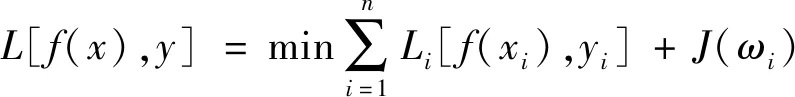
(3)
式(3)中:f(xi)、yi分别为第i组特征的预测值和真实值;ωi为第i组特征的常数项。
对于本研究中通过不同围岩特征预测多个支护参数的任务,如果将任务拆解成四个子任务分别预测锚杆间排距、锚杆长度、喷砼厚度、钢拱架类型,显然会忽略任务间的关联、冲突和约束,也会导致多任务的整体效果无法更优。为此,采用多任务学习(multi-task learning,MTL),将多个相关任务一起建模学习以便实现效果更优。相比单任务学习,多任务学习存在以下优势。
(1)多个任务共享一个模型,降低内存占用。
(2)同一模型一次计算出多任务结果,提升计算效率。
(3)任务间共享信息,提升模型效果。
为优化多任务学习预测效果,将多个单任务学习的损失函数累加,表达式为
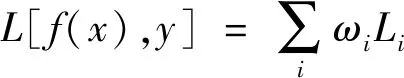
(4)
式(4)中:ωi为第i个任务在整个任务中的权重,如果每个任务权重均相同则为1;Li为各任务的损失函数。
2.2 多任务学习模型结构
关于锚杆间排距、锚杆长度、喷砼厚度、钢拱架型号的特征预测均为多分类任务,因此调用Keras模块中的多分类Softmax激活函数,模型语言及相应模块版本见表5。

表5 算法模型环境Table 5 Algorithmic model environment
为平衡模型性能和精度,模型加入三层激活层、两层dropout层用以弃置一部分神经元节点,避免模型过拟合造成较大误差[16],结构见图1。
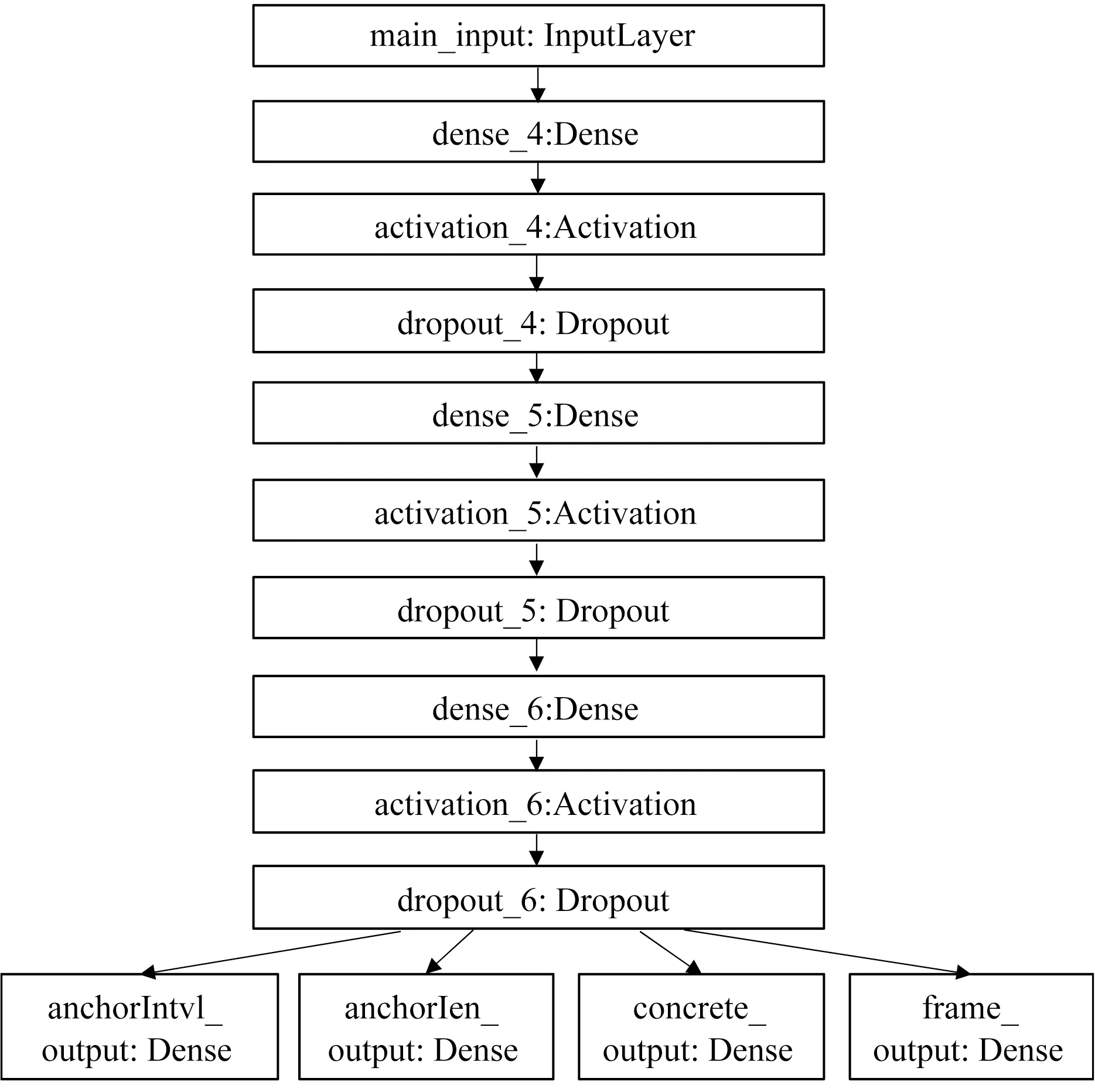
图1 模型结构图Fig.1 Model structure figure
2.3 多任务学习模型结果
结合1.3节数据与2.2节的模型结构训练模型,随机抽取约10%的围岩数据作为测试集评估模型预测效果,其中单次围岩数据见表6。
对比表7、表8中实际与预测参数可见,由围岩特征组1、4、6预测的参数较之实际更为保守。围岩特征7获得的预测参数与实际参数相同。由围岩特征组2、3获得的预测支护参数强度明显低于实际。
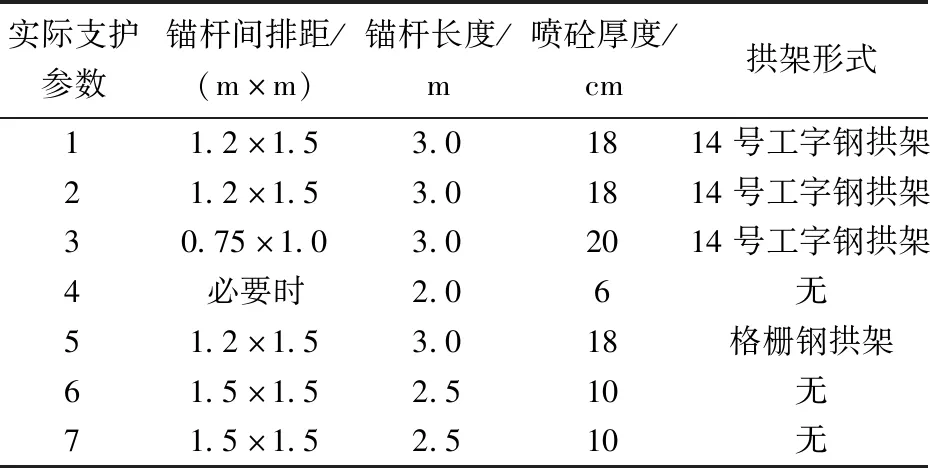
表7 实际支护参数Table 7 The actual support parameters
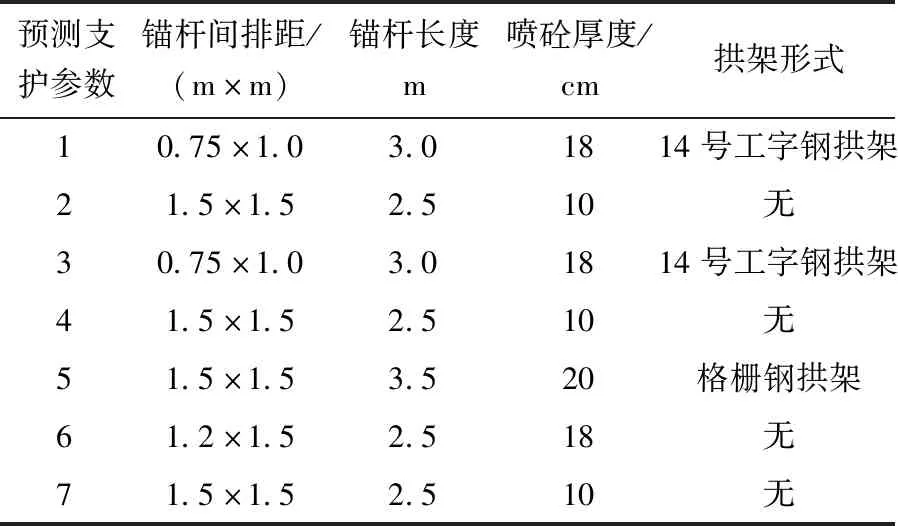
表8 预测支护参数Table 8 The predict support parameters
对于围岩特征组5,预测结果的锚杆间排距为1.5 m×1.5 m,显然要弱于实际的锚杆间排距 1.2 m×1.5 m。而预测的锚杆长度为3.5 m,喷砼厚度20 cm,显然强于实际的长度3 m,喷砼厚度 18 cm。因此,两方案的优劣有待进一步判断。
为进一步充分评估模型泛化性能,利用十折交叉法[17]抽取不同测试集进行8次模型效果评估,并按照预测参数较之实际参数强、相同、弱、各有强弱四种情况统计,结果见表9。各组预测参数强度高于或等于实际参数的比例分别为0.86、1、1、0.71、0.71、0.71、0.57、0.57,平均值为0.77。可见大部分模型预测参数强于实际。由于本次模型训练数据量较少,依然有部分预测结果低于实际支护参数,有待收集更多的现场数据迭代优化。
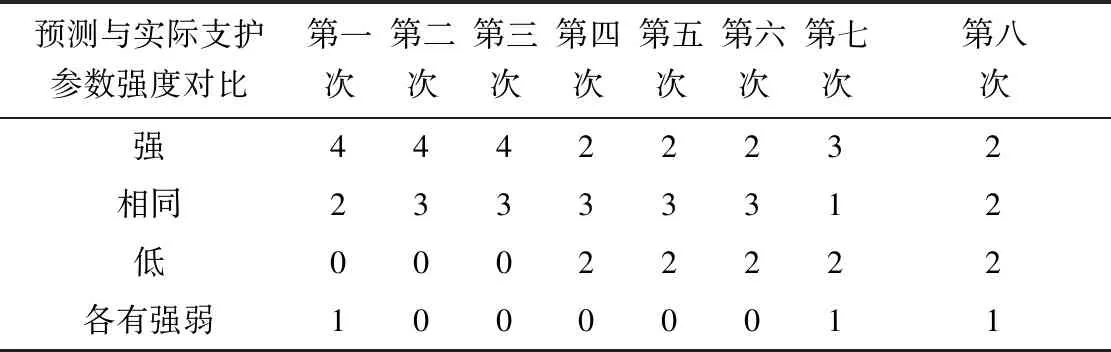
表9 预测与实际参数八次结果统计表Table 9 The statistical result between predict parameters and actual parameters in eight results
3 基于层次分析的支护方案评价
对于第2节中围岩特征5获得的预测和实际参数各有强弱的两套支护方案,如何评价其优劣是工程中一个亟待解决的问题。针对此问题,工程经验与专家会诊是常见的解决方案,部分学者更针对不同的支护方案数值建模计算评估效果。这不仅影响了评估的实时性,且泛化能力不足,无法完全覆盖工程中的各种支护设计。为此,借鉴之前研究后采用层次分析法[18]评估两种支护方案,以弥补以往支护方案评价中实时性和泛化性能不足的问题。
层次分析法建模,通常分为三个步骤:建立递阶层次结构、构建满足一致性检验的各层次判断矩阵、方案层的权重转换。
3.1 建立递阶层次结构
应用层次分析法分析问题,首先把问题条理化、层次化,构造一个有层次的结构模型。在此模型下,复杂问题被分解为多组成元素。这些元素又按属性及关系形成若干层次。上一层次的元素作为准则对下一层次相关元素起支配作用。
基于1.3节数据,将锚杆间排距、锚杆长度、喷砼厚度、钢拱架类型等最终的支护参数确定为方案层,也即最高层(第三层)。将围岩风化程度、坚硬程度、岩体完整程度、地下水状态、围岩稳定情况等与支护参数的相关性系数划分为第一层,用以表征各围岩特征对支护设计的总体影响程度。将风化程度、坚硬程度、完整程度、地下水状态、稳定情况对于围岩整体稳定性的影响权重划分为第二层,表征本研究中各围岩特征对于围岩整体稳定性的影响程度。
3.2 构建判断矩阵和一致性检验
基于表4数据,计算各支护参数对于围岩特征相关性系数的平均值,以此表征围岩特征变化时各支护参数响应的敏感程度。可知,各支护参数与围岩风化程度、硬度、岩体完整程度、地下水状态、围岩稳定情况的相关性系数平均值分别为0.63、0.33、0.39、0.05、0.48。
在Saaty层次分析法公式[19]中采取对因子两两比较建立矩阵的方法,即每次取两个比较因子xi和xj,以aij表示xi和xj的相关性对结果影响之比,例如坚硬程度与支护参数总体相关性为0.33,围岩风化程度与支护参数总体相关性为0.63,则坚硬程度相对于围岩风化程度对支护参数的相关性影响程度为0.33/0.63=0.52。显然判断矩阵A=(aij)n×n满足关系式
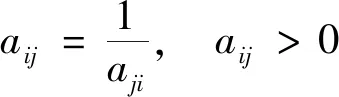
(5)
式(5)中:i,j= 1,2,…,n,n为特征数。
基于式(5)计算各围岩特征对支护参数的相对影响程度值,见表10。尽管表10能较为客观地反映两个影响因子的比重关系,但综合对比全部结果时却难免存在一定程度的非一致性。如果需要结果完全一致,判断矩阵A还应满足关系式
aijajk=aik
(6)
式(6)中:i,j,k= 1,2,…,n,n为特征数。
为保证式(6)成立,需对判断矩阵进行一致性检验。首先,计算获得表10所示矩阵的最大特征值λmax=4.993。通过式(7)获得一致性指标CI为-0.001 75。
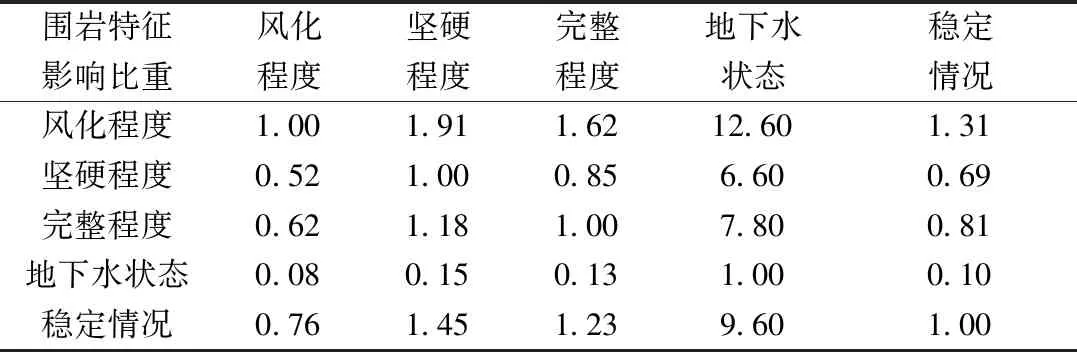
表10 围岩特征相对影响程度的判断矩阵Table 10 Judgment matrix of relativity about surrounding rock features
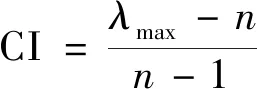
(7)
随后,结合特征数量根据平均一致性指标(表11),确定RI=1.12。进一步通过式(8)计算一致性比例CR=-0.001 56。

表11 平均一致性指标RITable 11 Mean consistency index RI
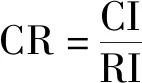
(8)
层次分析法理论认为CR<0.1时,判断矩阵的一致性是可以接受的。因此,认为当前判断矩阵的一致性符合要求。
进一步对表10矩阵中各列归一化后计算各行平均值,得到风化程度、坚硬程度、完整程度、地下水状态、稳定情况的相应权重矩阵A为

(9)
同理,可依次获得围岩特性对于各支护参数的判断矩阵,见表12~表16。根据式(7)计算得到表12~表16对应矩阵的CR分别为0.001 4、0.001 17、0.001 13、0.001 07、-0.000 6。显然依据式(8)可认为判断矩阵一致性均符合要求。
对表12~表16中判断矩阵进行列归一化后求每行平均值,获得各支护参数受围岩特征影响的权重矩阵B为
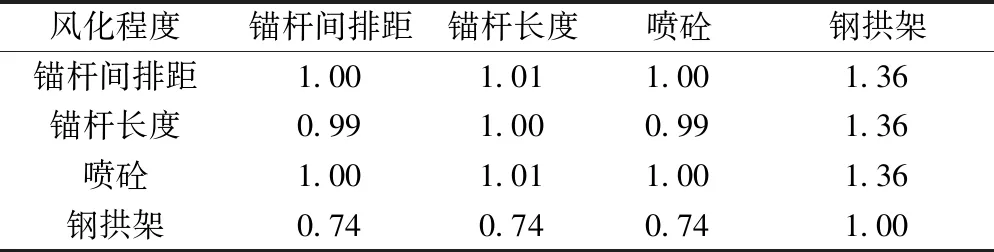
表12 风化程度对各支护参数判断矩阵Table 12 Judgement matrix of supporting parameters on decay
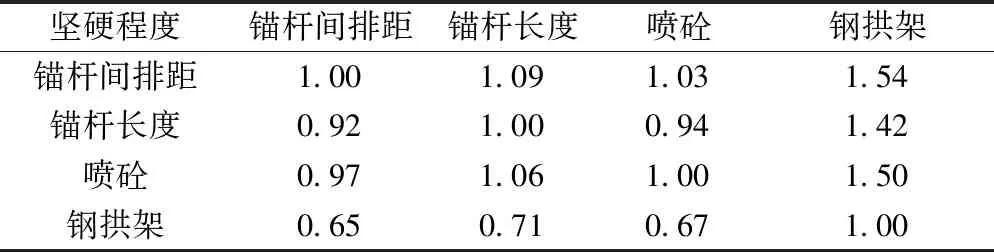
表13 坚硬程度对各支护参数判断矩阵Table 13 Judgement matrix of supporting parameters on hardness
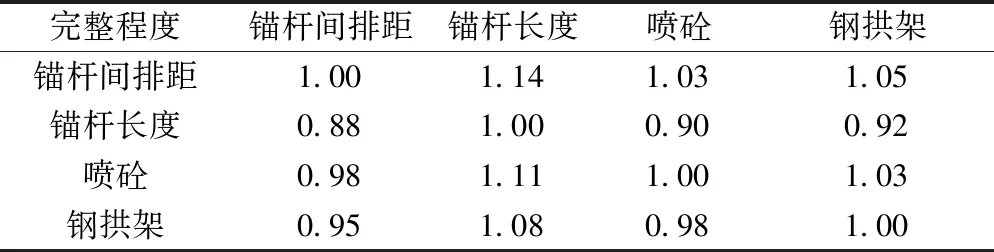
表14 完整程度对各支护参数判断矩阵Table 14 Judgement matrix of supporting parameters on integrity
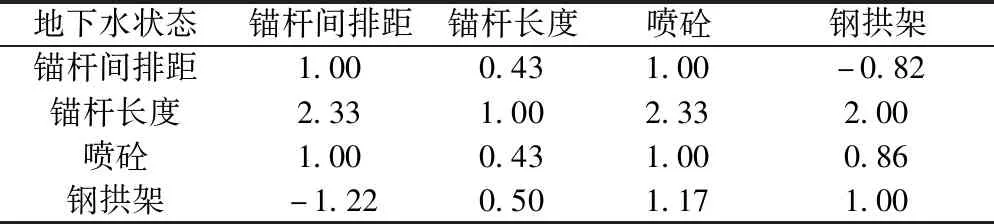
表15 地下水状态对各支护参数判断矩阵Table 15 Judgement matrix of supporting parameters on water
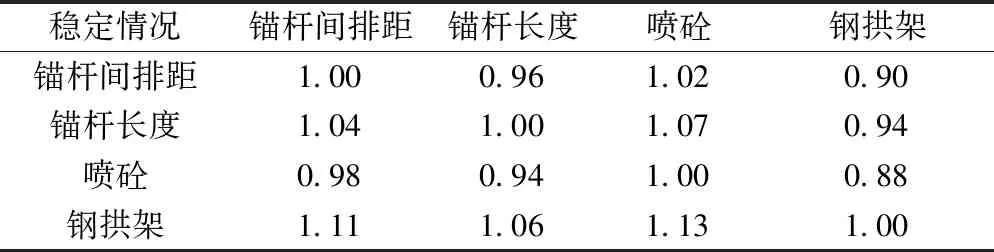
表16 稳定情况对各支护参数判断矩阵Table 16 Judgement matrix of supporting parameters on stability

(10)
3.3 支护方案层的结果表征
基于2.3节中多任务学习模型的计算结果,针对中风化、较坚硬岩、较完整、无掉块、无水的围岩特征(表6围岩特征5),多任务模型预测结果为[1,4,4,1],实际方案为[2,3,3,1]。
为对比两方案各支护参数的权重,首先初始化一个2×2的矩阵。令矩阵主对角线上元素为0.5,对于矩阵第一行第二列数字,如果方案二(实际支护参数)的效果优于方案一则取值为1,否则为0。同样对于矩阵第二行第一列的数字,如果方案一(预测支护参数)的效果优于方案二则取值为1,否则为0。针对本次预测和实际方案的4个支护参数,形成8×2的对比矩阵,即

(11)
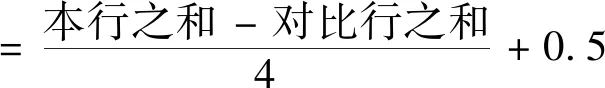
(12)
为避免两方案结果差异过大,同时考虑0在后期矩阵相乘计算时结果始终为0,利用式(12)对矩阵中非对角元素进行平滑,得到方案对比矩阵为

(13)
随后对各支护参数结果按列归一化,并对各支护参数结果按行计算平均值,得到预测与实际支护方案最终结果表征为

(14)
3.4 基于层次分析法的支护效果评价
综合围岩特征权重矩阵A和支护参数方案矩阵B,结合方案层矩阵W,计算两支护方案的综合评判值为
R=ABTW=[0.473,0.414]
(15)
根据最大优属度原则,预测支护参数得分为0.473,实际支护参数得分为0.414,可认为预测支护参数更为合理。
4 结论
首先分析了围岩特征与支护参数的相关性,通过构建多任务学习模型预测了支护方案,并通过层次分析法对比了支护方案效果,获得如下结论。
(1)通过数字化表征围岩特征与支护参数相关性,获得了各支护参数随围岩特征变动的响应敏感程度,结果表明支护特征受围岩风化程度变化影响最敏感,其次为稳定情况、完整程度、硬度。
(2)构建多任务学习模型预测了不同围岩特征下的支护参数,并通过十折交叉法评估了预测与实际支护参数的效果。在10组测试集中,预测参数强于实际的比例平均为0.77,可见预测结果大部分优于实际,模型对现场设计施工具有一定的指导意义。
(3) 基于围岩特征与支护参数相关性,采用层次分析法计算比较了预测支护参数与实际支护方案。结果表明预测方案得分高于实际方案,相比实际方案更具有优势。

