非饱和黄土场地水分入渗规律及影响因素的现场试验与数值模拟
张豫川,刘智璠,高旭龙,刘东发,黄鸿伟,赵野
(1.兰州大学西部灾害与环境力学教育部重点实验室,兰州 730000;2.兰州大学土木工程与力学学院,兰州 730000)
资源具有独特的时空差别,干旱年份有些地方总降水不足80 mm,过涝年份有些地方达到1 262 mm,年际变化十分悬殊且降雨量呈增加趋势[1],同时靠近水源的黄土台塬地区灌溉活动频繁[2],由于水分入渗作用导致的各类滑坡和工程地质灾害时有发生,因此对黄土地区的水分入渗规律进行研究非常具有必要性。
对此很多学者已经取得了丰硕的成果,白盛元等[3]进行半干旱区降雨入渗试验,发现水分随着深度增加,土体含水率变化逐渐滞后,增幅逐渐减小;潘振辉等[4]运用数值模拟手段研究地表入渗作用下土水特征曲线参数与边界条件对入渗结果的影响,探究了黄土中水分入渗规律;赵乐等[5]利用自主研发的一维土柱垂直入渗试验装置,分析了受干密度变化影响下的压实黄土垂直积水入渗特性;马鹏辉等[6]在不同深度裂缝处与非裂缝处布置监测仪器,并结合数值模拟手段分析裂缝对水分入渗的影响;关晓迪等[7]以甘肃某均质黄土边坡为原型,分析了不同坡比条件下降雨入渗过程和坡面冲刷现象,评价了不同坡比条件下降雨入渗规律的差异;Yao等[8]通过原位试验监测模拟降雨入渗和饱和入渗条件下土层含水率和崩塌变形等信息,为砂质黄土的水分物理作用和变形响应机制提供了新的认识;徐硕昌等[9]开展了重塑黄土的浸水入渗模型试验,分析了浸水过程中不同位置的体积含水率变化及湿润锋面发展过程,研究了入渗水分在水平和径向的发展变化规律;夏森林等[10]发现湿陷性黄土场地在有限雨水作用下水分的迁移作用范围和程度有限且呈不对称分布;温夏伟等[11]研究了覆被类型对黄土高原土壤水分的影响,发现了土壤水与植被之间存在一个平衡状态,当平衡状态被打破时,直接影响植被的生长,进而影响土壤水分的运动。张常亮等[12]在天然降雨入渗条件下对黄土中不同深度土层为期一年的体积含水率监测数据进行分析,发现浅部土层对降雨的反应敏感,土壤水分变化趋势同蒸发量和地表气温的变化趋势较为吻合;武小鹏等[13]对青海乐都黄土场地地基进行现场试坑浸水试验,得出水分在原状黄土地基内的竖向扩散速率和径向扩散速率均随着渗透距离的增加均呈减小趋势,入渗范围近似为一个“圆台形”或“喇叭形”;马闫等[14]对晋中地区黄土场地进行了打设注水孔的浸水试验,分析了水分在土层中的扩散规律是由上下两个方向共同向中间运移,且浸水影响范围与湿陷土层厚度的比值在1.6倍左右;陈静茹等[15]以西安地区黄土为研究对象,通过常规三轴剪切试验,研究了冻融循环对重塑黄土水分迁移的影响;潘俊义等[16]对边坡开展4种雨强下的野外人工模拟降水试验,分析并比较边坡浸水深度、土体含水率和边坡应力变化特征。
综合上述研究成果可以发现,试验地点的不同,土性的差异,水分入渗规律均会有所区别,在天然降水条件下黄土土体水分入渗深度及宽度是有限的。同时大多数的水分入渗研究是对某一地点进行某一水量的研究,没有考虑水分入渗形式及水量的差异影响。现依托某非饱和黄土场地浸水试验,探究水分入渗规律,结合数值模拟研究浸水类型及水量对水分扩散规律的影响,为类似黄土地区因浸水引发的工程地质及滑坡等灾害提供依据。
1 试验场地概况
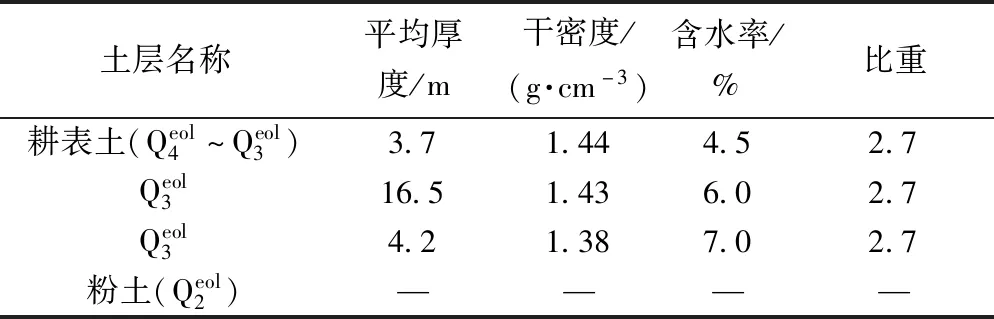
表1 试验场地的土层特征及物理力学指标Table 1 Characters and physical and mechanical parameters of soil layers
2 现场试验设计
2.1 浸水坑尺寸及水分计安置
浸水坑平面为椭圆形,长、短轴分别为30、20 m,试坑底面深度为-0.7 m,开挖1#、2#、3#和4#探井用以埋设水分计,水分计埋设位置为沿长轴方向距离探井侧壁1 m,试坑尺寸、探井及水分计位置如图1所示。水分计在上述位置的不同深度交错布置,以全面获取地层的水分入渗信息,具体见如图2所示。水分计通过在探井侧壁掏孔埋设,在设计深度处采用小型洛阳铲向探井侧壁掏土,掏土深度为1 m,将水分计探针插入孔深处原状土体直至探针完全没入,向孔内回填土体并培实,保证密实度与原始土体接近。同一位置不同深度处的水分计埋设完毕后,进行探井回填,每层虚填30 cm,夯实回填至探井顶部,顶部用灰土做封顶处理。仪器埋设完毕后,在试坑表面铺设10 cm厚砂砾层,保证水分均匀入渗。
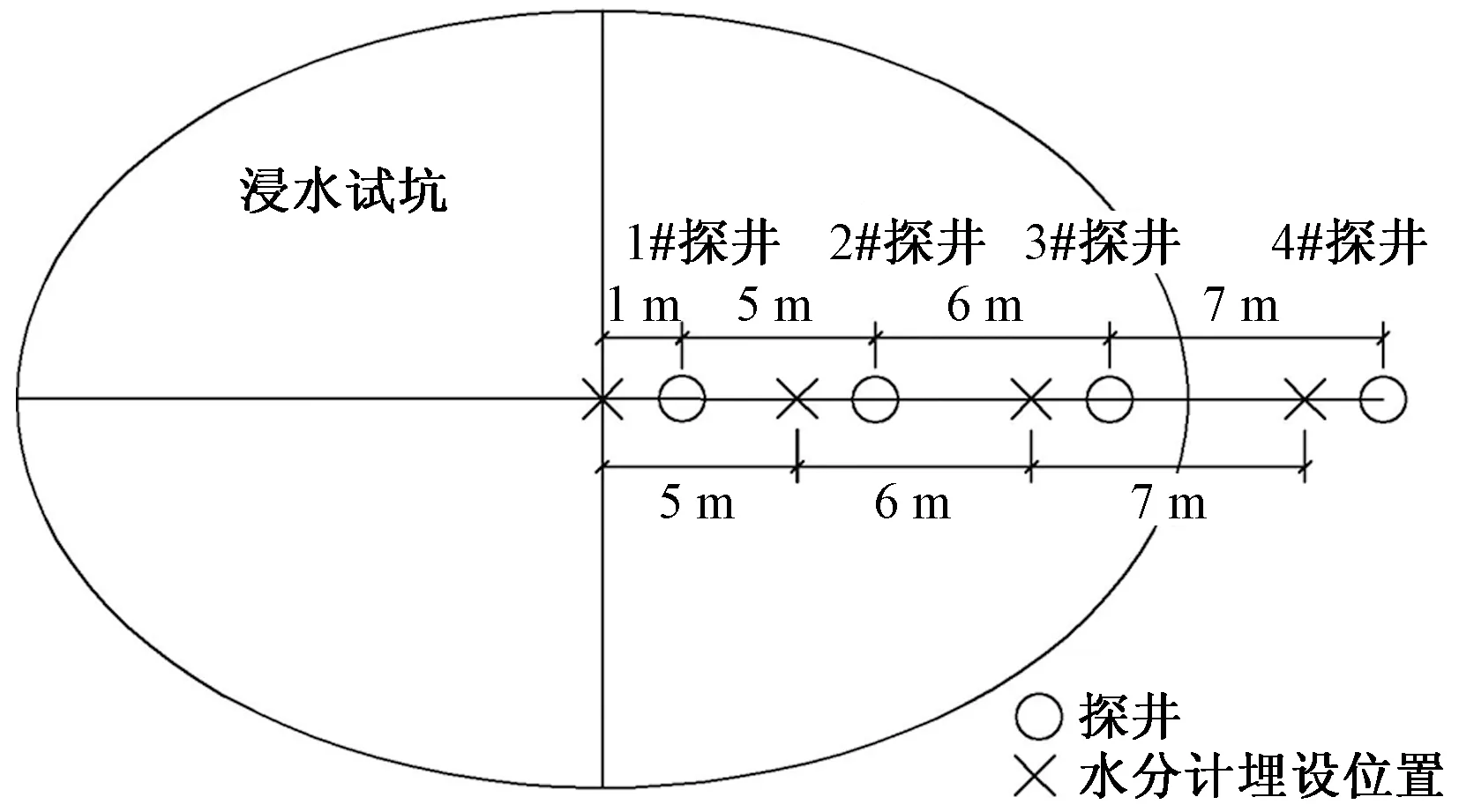
图1 浸水试坑平面图Fig.1 Sketch of immersion pit
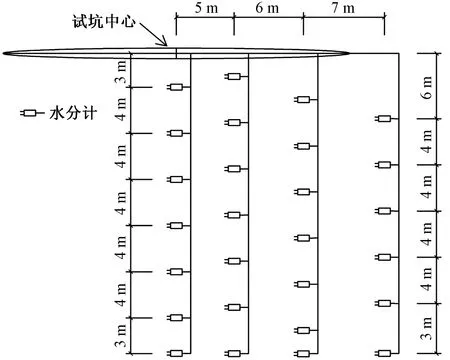
图2 水分计安置方位图Fig.2 Location of moisture meter
2.2 试坑浸水及数据采集
为使试坑平面浸水均匀,采用管道喷淋方式浸水。在椭圆轴端距离试坑边缘3 m处安置容积为60 m3的卧式圆柱体水罐,每个水罐负责1/4椭圆面积浸水,如图3所示。水罐底部的出水管道与输水管道连接,输水管道为内径3.8 cm、壁厚2 mm的塑料软管,管道表面间隔1.2 m设置直径为2 mm的喷淋孔。输水管道布设间隔0.6 m,在椭圆的拐角处增大弧度,避免管道弯折导致水流阻塞。输水管道布设完毕后,开启或关闭出水管道的阀门实现试坑场地浸水及停水。试验时间为2019年9月21日—10月22日,共计32 d,其中浸水阶段时间为9月21—27日,共计7 d,浸水停止后继续监测至10月22日,共计25 d。浸水阶段每天水量为90 m3,共计浸水量630 m3,为当地最大年降雨量的3倍。

图3 现场试验图Fig.3 Picture of field test
2.3 体积含水率变化规律
以试坑中心1#探井-3 m和-7 m位置处水分计监测到的水分信息为例阐述土体体积含水率变化规律,如图4所示,土体体积含水率随时间关系曲线均呈现出4个阶段变化特征:稳定段ab、上升段bc、快速下降段cd和缓慢下降段de。稳定段ab体积含水率始终为9.8%,表明土体始终保持天然含水率状态,水分未入渗至水分计埋设位置,-3 m和-7 m这一阶段时间分别为3 d和13 d。上升段bc表明上部土体中的水分入渗至相应位置,b点为体积含水率随时间变化曲线的第一个拐点,表示着湿润锋到达埋设点位置[13],随着时间的增加,体积含水率增加的速率逐渐减小,在达到顶峰c点之前,水分入渗呈先快后慢趋势。这主要是因为:①土体逐渐接近饱和,黏粒表面的结合水膜变厚,粒间以斥力为主,阻碍了自由水分的向下入渗;②随着浸水试验的发生,上部土体可能发生自重湿陷,湿陷导致上部土层压密,空隙变小,进一步阻滞水分扩散和渗入。因此,在该阶段曲线的斜率逐渐减小[17]。-3 m和-7 m这一阶段时间分别为3 d和10 d;快速下降段cd表明在此阶段水分向更深位置的土体消散,体积含水率快速下降,-3 m和-7 m这一阶段时间分别为18 d和16 d;缓慢下降段de体积含水率降低速率较cd段小的多。
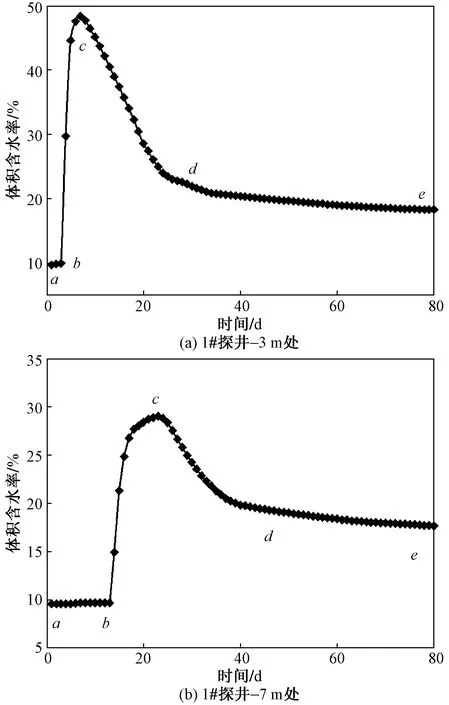
图4 试坑中心-3 m、-7 m深度土体体积含水量变化Fig.4 Changes of volume moisture content for soli with depth of -3 m and -7 m in the center of test pit
同时可以看出,-3 m处土体体积含水率最大值为48%,接近饱和状态,而-7 m位置土体体积含水率最大值为29.3%,试验全过程中始终没有达到饱和。结合其他不同位置水分计监测信息,只有1#探井-3 m位置,2#探井-2 m位置,3#探井-4 m位置三处土体达到饱和,可见降雨入渗条件下,水分饱和入渗的深度是有限的,只是在浅层形成了似富水带。浸水过程中因入渗水源不断补给,富水带已有水分向深部迁移的同时存在上部补给水分地不断流入,富水区逐渐扩大。停水使得入渗水源补给消失,此时富水带水分继续向下迁移入渗,入渗深度仍在扩大,但富水区因自身水分逐渐丧失并变为非饱和区域。综合不同位置处的水分计监测信息可以发现,体积含水率变化均为上述四个阶段特征,区别在于各阶段时间的长短和体积含水量峰值的大小,对于浅部土体,稳定段ab时间较短,体积含水率峰值较大,快速下降段cd段较陡。
2.4 浸润锋扩散规律
将两个竖向相邻水分计之间的距离除以浸润锋在这两点之间的运移时间即为水分在两点之间土层的竖向平均扩散速率。1#探井土层竖向平均扩散速率如表2所示,可以发现,随着土层深度增加,渗透时间不断增加,竖向平均渗透速率逐渐减小,0~-3 m土层到-11~-15 m土层渗透时间从4 d增加至23 d,竖向平均扩散速率从8.68×10-4cm/s降至2.01×10-4cm/s。

表2 土层竖向平均扩散速率Table 2 Average vertical diffusion rate of water in soil layer
3 数值模拟
3.1 有限元模型建立
现场试验由于耗时长、费用高等因素限制无法实现长时间、多工况的研究工作,结合土样室内试验和现场监测结果并借助数值模拟手段可以在时间上加以延伸,同时可以研究不同浸水类型及不同水量条件下黄土中水分入渗特征及扩散规律。为对应现场试验,模型尺寸为60 m×40 m,入渗边界长30 m,坑深0.5 m,网格划分长度为0.4 m,节点数28 502个,单元数28 351个,左、右和下边界为不透水边界,如图5所示。根据前期地层勘察得知,试验场地覆盖层为厚度较大的夹砂粉质黄土,土质较为均匀,因此将土层设置为均质黄土(L1),初始含水率为9.8%,地下水位大于50 m,不考虑地下水对模型区域的影响。
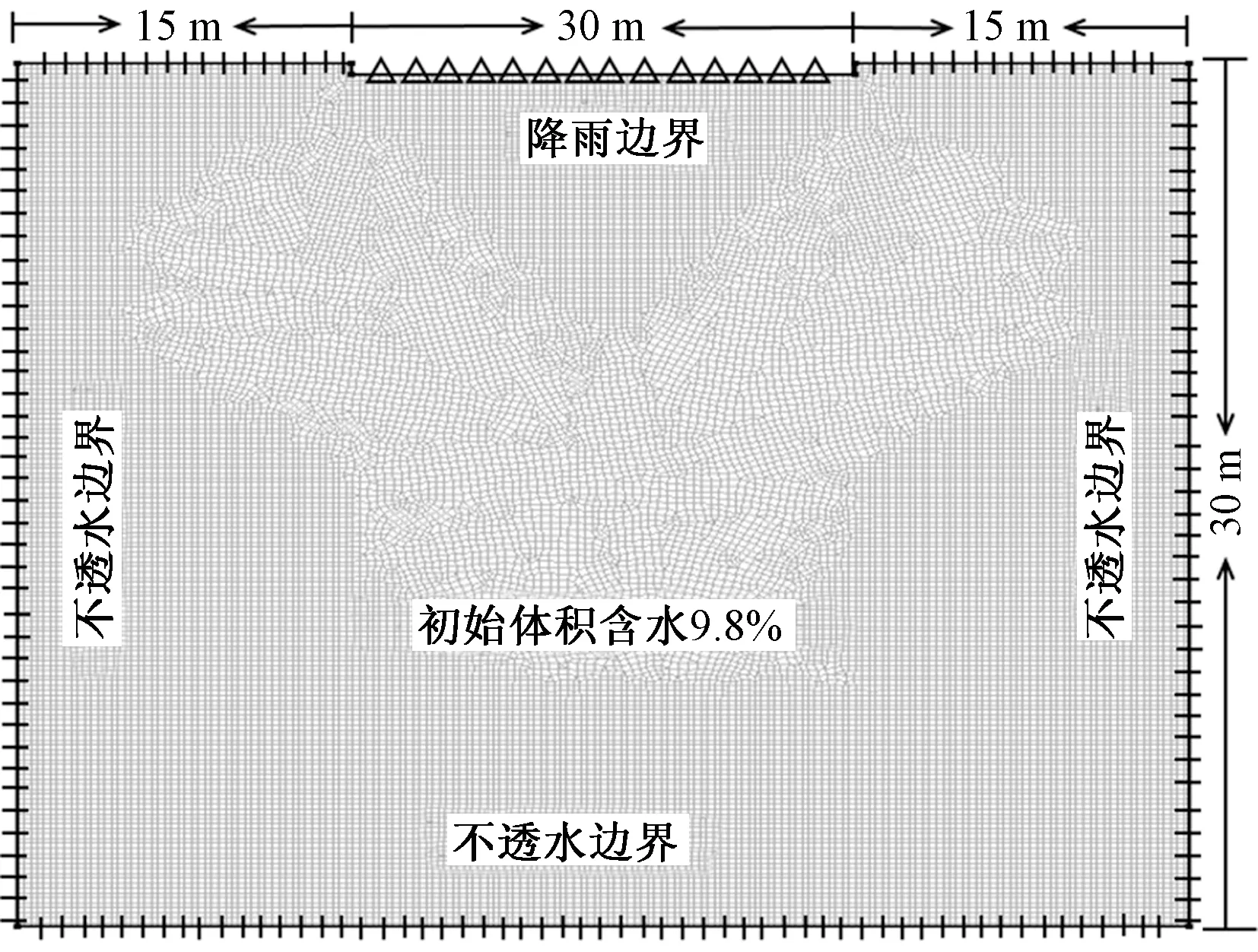
图5 有限元网格建立及边界设置Fig.5 Establishment of finite element mesh and boundary setting
3.2 模型参数选取
3.2.1 土水特征曲线
对非饱和渗流问题进行数值模拟,需要确定土体的土-水特征曲线和考虑含水率变化(或基质吸力)的渗透系数函数,上述曲线和函数能否真对非饱和渗流问题进行数值模拟,需要确定土体的土-水特征曲线和考虑含水率变化(或基质吸吸力)的渗透函数,上述曲线能否真实地反映试验场地土体的性质直接影响到模拟结果的准确性。对探井原状土样进行室内试验,并采用Van Genuchten模型[18]对试验所得数据进行拟合以获得土水特征曲线,拟合方程为
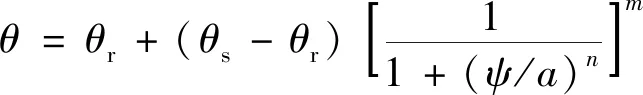
(1)
式(1)中:θ为体积含水率;θr为残余含水率;θs为饱和含水率;ψ为基质吸力;a、n、m为表示土水特征曲线的相关参数,具体取值如表3所示。

表3 土水特征曲线的模拟参数Table 3 Simulation parameters of soil-water characteristic curve
3.2.2 非饱和渗透系数
VG的渗透系数函数kr(ψ)解析表达式为
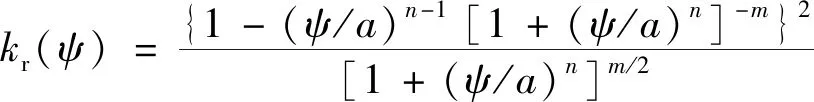
(2)
将测定的土-水特征曲线和渗透系数函数带入至模型中计算发现能和现场监测结果有良好的对应,土-水特征曲线及基质吸力-渗透系数函数如图6、图7所示。
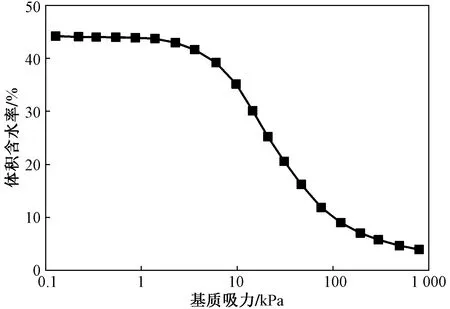
图6 土-水特征曲线Fig.6 Soil-water characteristic curve
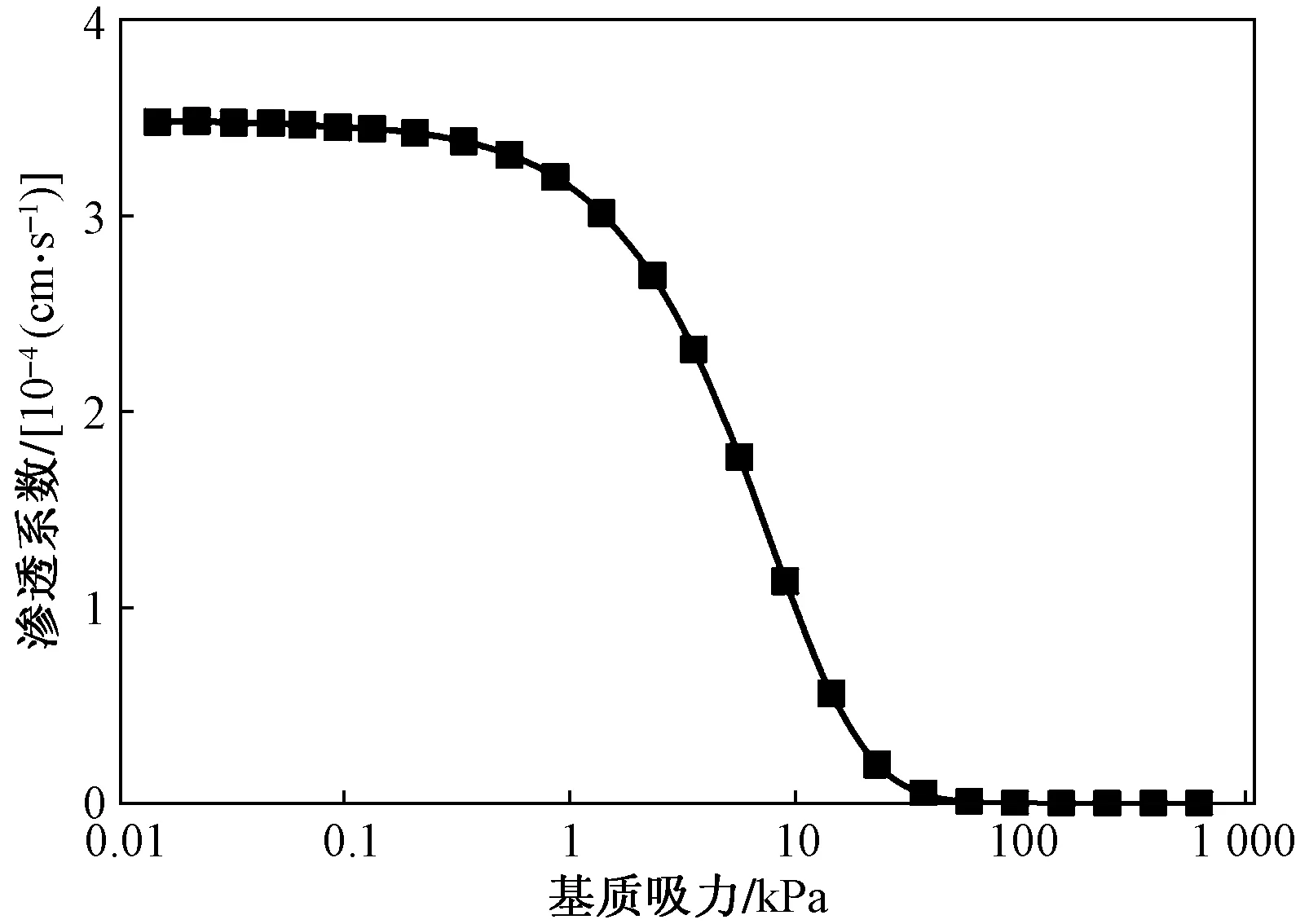
图7 渗透系数函数Fig.7 Permeability coefficient function
3.3 不同浸水类型黄土水分扩散规律
将浸水分为“平均型”“上峰型”“下峰型”和“中峰型”4种类型,分析600 m3水量时4种浸水类型黄土水分扩散特征,图8为4种浸水类型及每种类型的水量随时间变化柱形图。
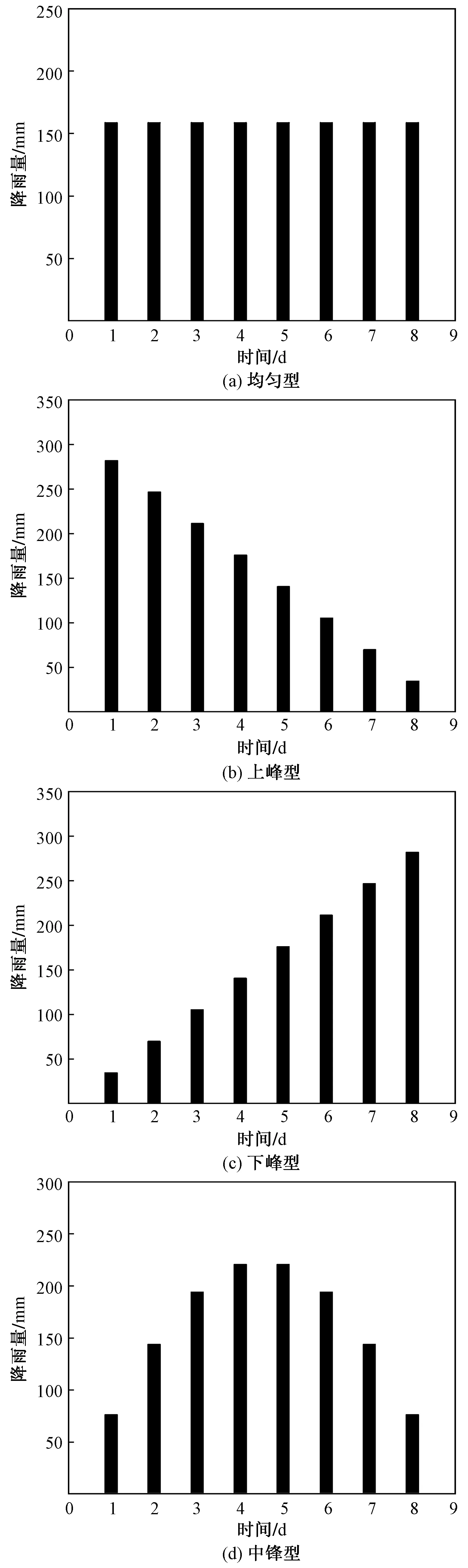
图8 不同浸水类型及水量随时间变化Fig.8 Different types of water immersion and water volume change with time
由2.3节所述,土体体积含水率开始变化代表湿润锋到达埋设点位置,在数值模拟中当土体的体积含水率由初始值9.8%升高至12%即可认为水分入渗至土体,即浸润锋到达土体所在位置,图9为4种浸水类型在10、30、50、100、150、200 d浸润锋扩散图,可以看出,4种浸水类型浸润锋扩散形态相同,均以椭圆形扩散(长轴为水平向)。
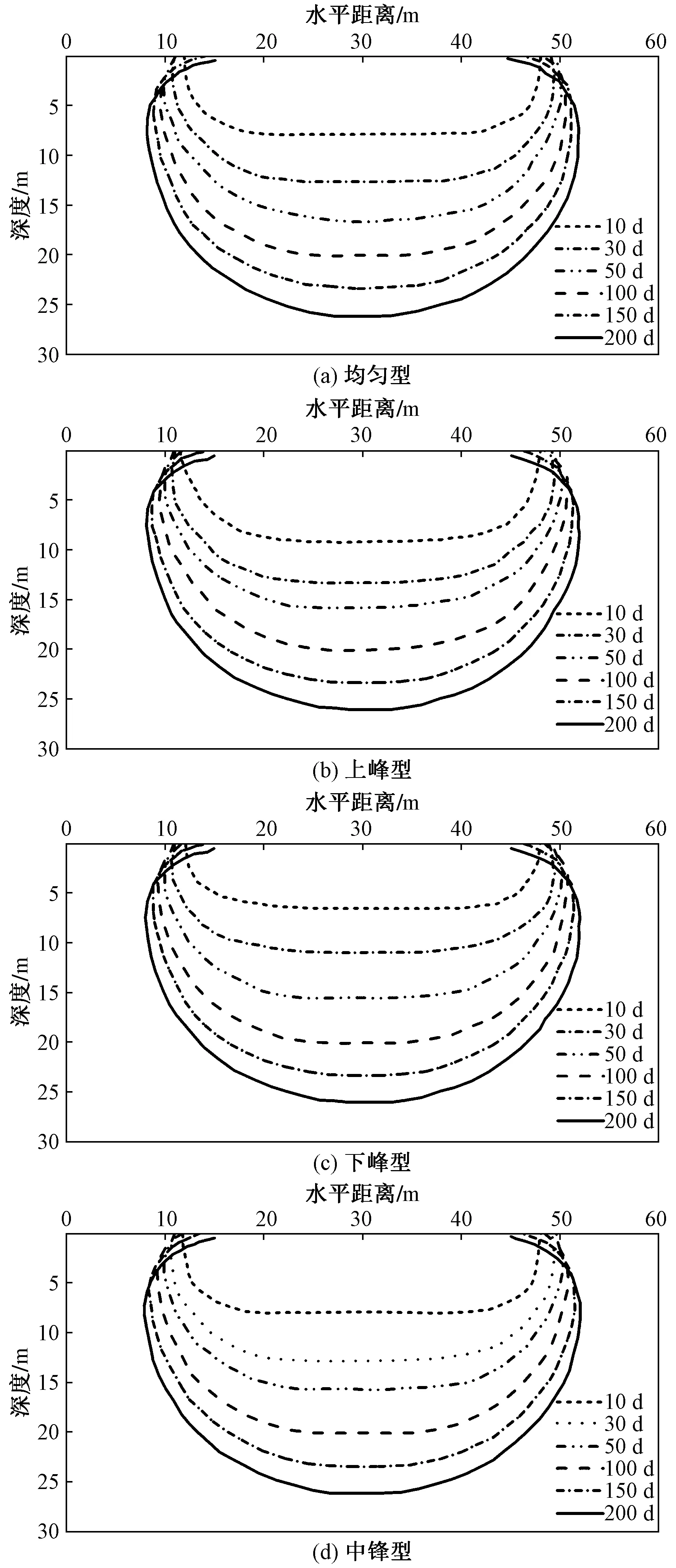
图9 不同浸水类型浸润锋扩散图Fig.9 Diffusion diagram of infiltration front of different precipitation types
图10为不同浸水类型入渗深度及宽度随时间的变化。“均匀型”和“中锋型”在不同天数时的扩散范围基本相同,表明这两种浸水类型入渗特征较为一致。“上峰型”入渗深度及宽度在30 d内比“均匀型”和“中锋型”大,“下峰型”入渗深度及宽度在30 d内比“均匀型”和“中锋型”小,这是缘于当较大的水量出现在前期时,非饱和土体在短期内水量入渗相对较快,导致入渗深度及宽度较大。在50 d时4种浸水类型入渗深度及宽度达到一致,随着时间的继续延长,入渗深度及宽度增加保持一致。由此可以看出,当浸水量相同时,不同浸水类型的入渗深度及宽度在短时间内会存在差异,然而对最终入渗深度及宽度并没有影响。
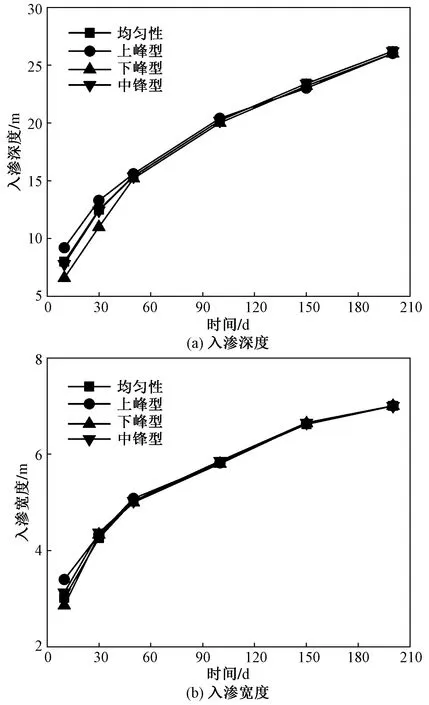
图10 不同浸水类型入渗深度及宽度随时间的变化Fig.10 Variation of infiltration depth and width of different precipitation types with time
3.4 不同浸水量水分扩散特征
分别模拟了浸水类型为“均匀型”,水量为300、600、900、1 200 m3时在200 d内的水分扩散,将4种不同水量在50、100、150 、200 d时的浸润锋扩散形态画出,如图11所示。
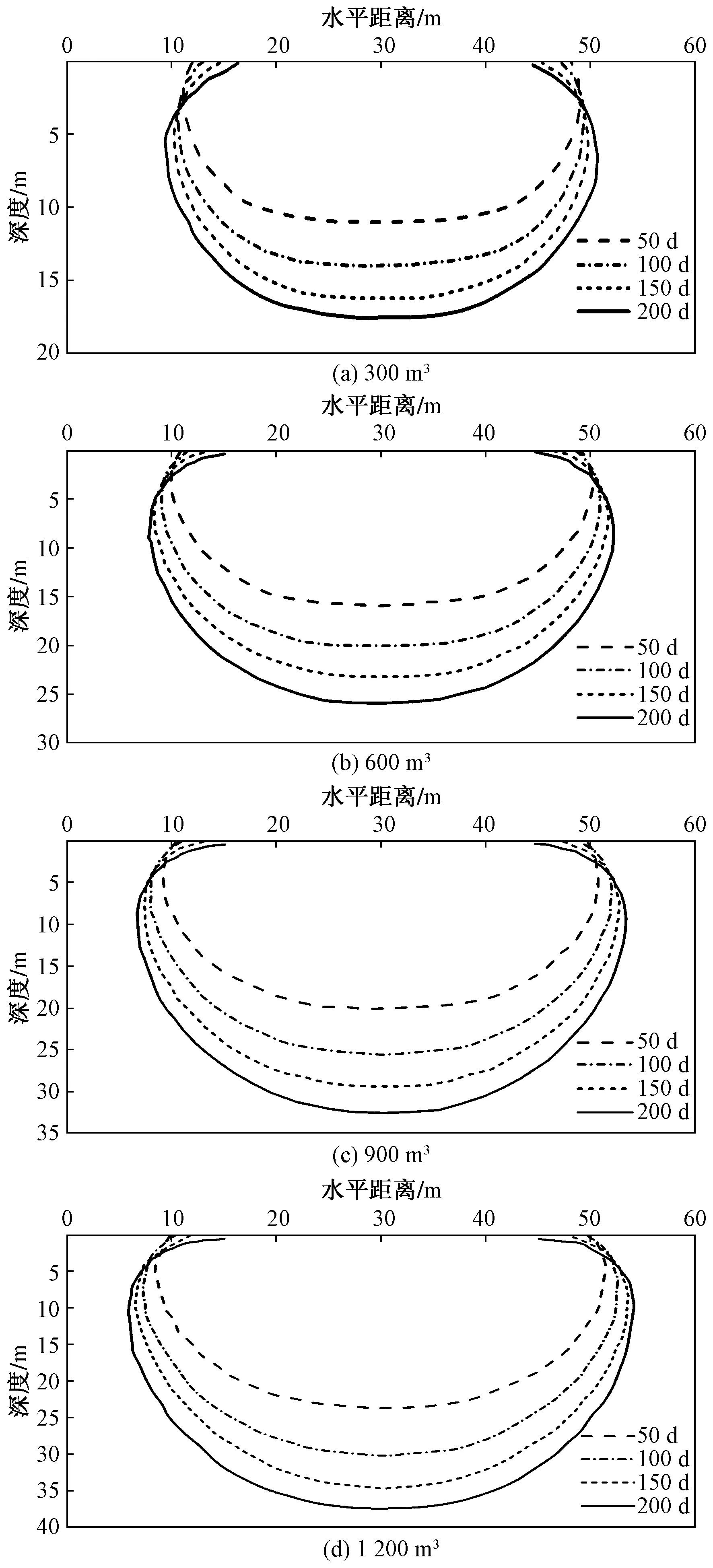
图11 不同水量水分扩散图Fig.11 Water diffusion diagram of different water immersion amount
从图11中可以发现50 d内水分入渗深度及宽度较大,4种浸水量在50 d内入渗深度及宽度均为200 d的60%左右,表明在浸水发生的短期时间内,水分入渗速率较快,入渗深度及宽度较大;随着时间的延长,入渗速率减缓,相同时间间隔水分入渗深度及宽度逐渐减小,这与文献[9]中描述的重塑黄土竖向水分入渗规律一致。入渗速率减缓的原因有:①入渗初期,渗流路径较短,水分补充充足,入渗较为迅速,且土体表面与大气联通,空隙气体可以自由逸出;②随着时间的推移,深度的增加,土体内部变成了封闭系统,进入土中的水分不断压缩土体空隙中的气体,使得各深度处的气压增长,同时反作用于水流,阻滞了水分的向下入渗;另外,如2.3节所述,粒间斥力的增大以及上部土体的湿陷也是导致入渗速率减缓的重要原因。
图12为4种浸水量在不同时间的浸润锋扩散深度、宽度变化,200 d时4种浸水量的入渗深度分别为17.5 、26.2、32.5、37.4 m,比前一级分别增加了49.7%、24.0%和15.1%,入渗宽度分别为5.5、7.1、8.3、9.0 m,比前一级分别增加了29.1%、16.9%和8.4%,由此可以看出,随着浸水量的增加,该非饱和黄土场地水分入渗深度及宽度增加幅度逐渐减小,入渗宽度变化更加明显。主要原因是,受土体内不同作用力的影响,竖向水分的运移实际上是本深度层重力、吸力和上部水压三力共同作用的结果,而径向入渗只有吸力和上部水压。两者相比,压力势在竖向和径向数值大小相等,而吸力势与重力势相比却小的多,随着水分扩散至较深土体部位时,吸力势会进一步降低[19],使得水分径向运动受到限制,阻滞水分的运移;另外,试验场地所属的砂质黄土,相比一般黄土粒径更大、吸力更小,入渗宽度增加幅度的变化可能与此也有着重要关系。推测入渗深度及宽度的界限值分别为43 m和10 m左右。
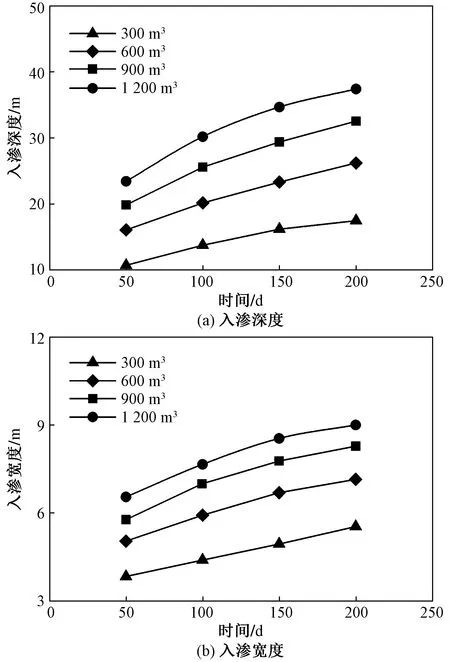
图12 入渗深度及宽度随时间的发展Fig.12 Development of infiltration depth and width with time
同时不可忽略的是,在0~-5 m深度范围内,水分水平向扩散距离呈先增大后减小的趋势。这是由于在浸水发生的短期时间内,浅层土体水分含量较高,水平向入渗率较大导致水分扩散距离较远,随后随着土体孔隙中的水在重力和基质吸力作用下向下运动,含水量逐渐降低,水平向扩散距离减小。
4 结论
(1)非饱和黄土场地在浸水条件下,不同深度处土体的体积含水量变化均呈四阶段特征,区别在于各阶段时间的长短和体积含水量峰值的大小。
(2)湿润锋以椭圆形状扩散,水分扩散速率随深度及宽度的增加越来越慢,其中水平向变化更加显著。
(3)浸水过程中,浅层土体会产生一定范围的富水区,停水后富水区的水分不断向四周土体扩散,整个水分到达区域呈非饱和状态,降雨条件下场地渗流以非饱和入渗为主。
(4)不同浸水类型的入渗深度、宽度在短时间内会存在差异,然而对最终入渗深度、宽度并没有影响。随着浸水量的增加,黄土中水分入渗深度和宽度不断增加,但增加幅度不断减小。

