高速公路收费站车道功能及方向优化模型

宋浪，俞山川，王少飞，安文娟

(1.招商局重庆交通科研设计院有限公司，重庆 400067；2.哈尔滨工业大学交通科学与工程学院，哈尔滨 150090)

2019年起中国逐步加快推进电子不停车快捷收费的推广应用，且根据《取消高速公路省界收费站总体技术方案》要求，未来实现高速公路开放式无站自由流收费。电子不停车收费(electronic toll collection,ETC)系统的便利性和快捷性促进其推广应用，ETC用户数和使用率正在逐步增加，但目前ETC的使用率不足以支持取消人工半自动收费(manual toll collection,MTC)车道，使得收费站ETC、MTC车道混合设置长期存在。故需结合收费站交通量、交通组成和ETC使用率，科学合理地设置收费广场车道配置方案，以保证收费站通行效率。

姬杨蓓蓓等[1]以建设运营成本和延误成本最小为目标建立优化模型，探讨在不同流量和ETC比例下收费站的合理建设方案。杨涛等[2]根据车辆类型和不同支付方式服务时间修正得到车道的实际通行能力，以此实现建设期车道数优化计算。随着自动驾驶技术的兴起，未来需考虑高速公路自动驾驶车辆收费车道的设置，为此Yu等[3]探讨不同自动驾驶车辆占比下收费站车道配置。以上研究探讨的是建设期的车道配置方案，而运营期更多关注车道的开放数量和车道的使用功能。

林培群等[4]以收费站运营成本和用户延误成本最小为目标，研究收费站车道类型组合开放方案。钱超[5]等构建了包含跟驰和变道行为的收费广场交通行为模型，并由此提出了收费广场车道合理配置方案。Wang等[6]选取排队长度作为收费站拥堵的评价指标，从而给出不同流量下收费站车道开放方案。Kim等[7]研究了收费广场的最佳车道配置，并制定策略将车辆引导到排队较短的车道。崔洪军等[8]考虑运营成本和排队成本，探讨收费车道开启方案。上述研究是一种车道功能优化方案，通过调整ETC/MTC混合车道的使用功能，以达到收费站整体通行效率最优，但并没有突破收费站出口或入口的容量限制。还有学者针对收费站混合车道通行能力、几何设计等方面展开了研究[9-12]。

近年来，随着人民生活水平的不断提高，居民节假日和周末定期选择郊区旅游或回乡的现象越来越明显，使得一些临近城区的高速公路收费站存在显著潮汐现象，假期开始以出城上高速交通需求为主，假期结束以返城下高速交通需求为主。为此，部分收费站试点开设了“潮汐车道”的潮汐收费岛，以缓解通行压力，这属于一种车道方向优化方案。

另一方面，为从根本上解决收费站拥堵问题，部分省市出台了收费站拥堵免费通行政策，但由于相关研究较少，使大多数拥堵免费通行的规定较为模糊。崔志宾等[13]提出了考虑车道长度和车道面积折算的免费放行位置计算方法。而冯晓燕等[14]基于排队论发现，当收费广场排队长度超过一定值，排队车辆将无限排列下去，故免费通行位置的设置需参考此值。此方法确定的免费放行排队长度值较大，适用于收费站开足收费车道仍存在拥堵现象的情况。但对运营单位为节约运营成本，故意未开足收费车道而导致拥堵的情况，需要同时考虑用户延误成本和收费站免费放行损失成本。

为此，借鉴城市交叉口逆向可变车道、借道左转车道等车道控制思想[15-16]，通过动态调整收费广场车道功能和切换车道收费方向，将其建立到一个统一的优化模型中，以适应不同流量场景，在不扩建收费广场的情况下突破收费站出口或入口的容量限制，实现“智慧扩容”。并对比分析用户延误成本和收费站免费放行损失成本随免费放行排队长度阈值的变化情况，以通过平衡上述两种成本给出收费站免费放行判定标准。

1 基本概念与车道配置过程

基于车道的收费广场车道配置如图1所示，从出入口各自行车方向的最右侧往左连续设置相应的收费车道，使得在收费广场中间车道形成双向收费，车道的收费方向和使用功能可根据预测的交通量选择配置。在运营期，通过动态调整MTC/ETC混合车道的使用功能，同时动态切换车道收费方向，以平衡收费站出入口交通需求，缓解单向拥堵，为“潮汐收费车道”和混合车道的开放提供理论依据。

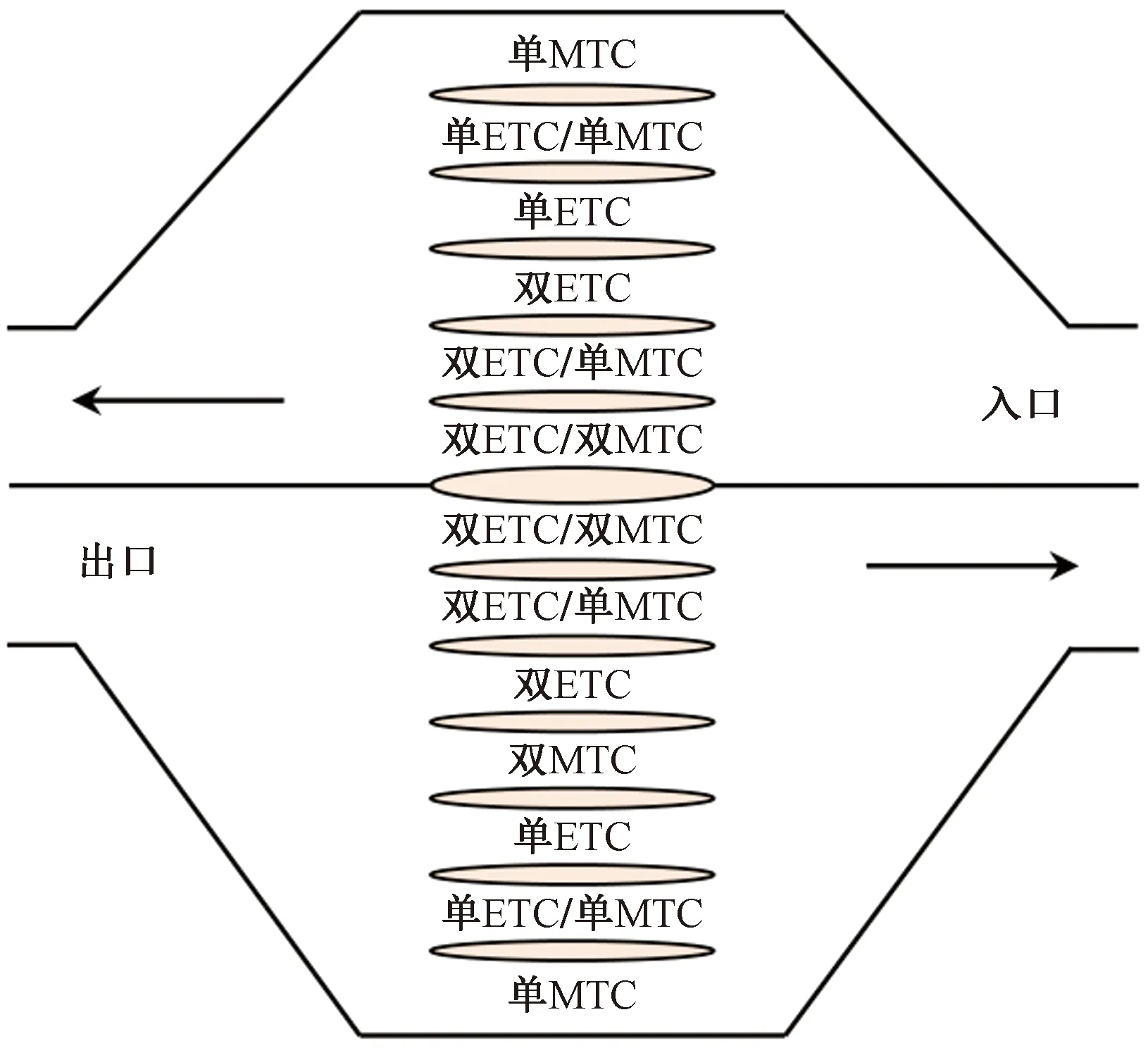
“双”“单”分别表示车道是否可切换方向图1 收费广场车道布局Fig.1 Layout of toll plaza

2007年颁布的《收费公路联网收费技术要求》给出了收费车道数计算依据，首先换算得到设计小时交通量，结合服务时间理论值，在设计要求的平均等待车辆数下，从车道数表格选取合适数值。但只适用单一收费制式，对于混合车道和双向车道需进一步分析，基于车道的收费广场设计阶段车道配置过程如下。

Step 1根据《收费公路联网收费技术要求》等，针对不同流量场景下的交通需求和ETC使用率，给出相应流量场景收费广场出入口MTC、ETC车道数；

Step 2分别寻找所有流量场景中收费广场、出口和入口总车道数最大值N、Nc、Nr，其中N作为收费广场设计车道数，Ns=Nc+Nr-N为双向收费车道数，Nc-Ns、Nr-Ns分别为单向出口、入口车道数。

Step 3分别寻找所有流量场景中出口MTC、出口ETC、入口MTC和入口ETC车道数最大值NcMTC、NcETC、NrMTC、NrETC，其中，Ncs=NcMTC+NcETC-Nc,Nrs=NrMTC+NrETC-Nr分别为出口和入口MTC/ETC混合车道数，NcMTC-Ncs、NcETC-Ncs分别为出口MTC、ETC单一车道数，NrMTC-Nrs,NrETC-Nrs分别为入口MTC、ETC单一车道数。

在设计阶段车道配置基础上，结合基于车道的收费广场车道功能和车道方向控制思想，建立运营期收费广场车道开放优化模型。

2 优化模型

2.1 目标函数

2.1.1 收费站运营成本

MTC车道运营成本包括设备运行成本、材料购置成本和人工成本[4]，材料购置成本按每辆车收费耗材计算。ETC车道运营成本即设备运行成本。则收费站运营成本计算公式为

Cjk=C′1+C′2λjk/yjk+C′3,∀j;k=1

(1)

Cjk=C′4,∀j;k=2

(2)

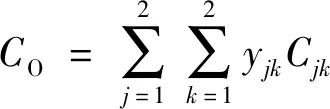
(3)

式中：C′1为MTC设备运行成本，元/h；C′2为材料购置成本，元/veh；C′3为人工成本，元/h，按每月工作22 d、每天工作8 h换算得到；C′4为ETC设备运行成本，元/h；Cjk为方向j功能k车道运营成本，元/h；CO为收费站运营成本，元/h；yjk为收费车道开放为方向j功能k的车道数；λjk为选择方向j功能k缴费的交通需求，veh/h；j为车道方向，j∈{1,2}分别表示出口、入口；k为车道功能，k∈{1,2}分别表示MTC、ETC。

2.1.2 用户延误成本

延误成本是车辆因排队等待造成的时间损失费用，姬杨蓓蓓等[1]分为客车延误成本和货车延误成本计算，并将多种车型延误成本加权平均换算为单车平均延误成本，杨涛等[2]同样采用加权平均法将多种收费方式服务时间换算为单车平均服务时间。故用户延误成本计算公式为

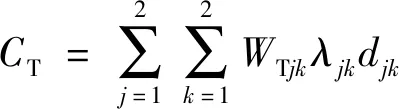
(4)

式(4)中：djk为平均等待时间，h；WTjk为车辆平均成本系数，元/(h·veh)；CT为用户延误成本，元/h。

2.1.3 收费站免费放行损失成本

中国多个省份都出台了收费站拥堵免费通行政策文件，例如，《广东省公路条例》规定“因未开足通道而造成在用通道平均五台以上车辆堵塞的，应当免费放行并开足通道”；《江苏省高速公路条例》规定“因未开足收费道口而造成平均十台以上车辆待交费，或者开足收费道口待交费车辆排队均超过二百米的，高速公路经营管理单位应当免费放行，待交费车辆有权拒绝交费”。通行费收取对运营单位有着重要作用，直接影响运营单位收费车道开放策略，需在优化模型中考虑。当出口各种车道平均排队车辆数超过一定值，运营单位应免费放行，收费站免费放行概率和损失成本为

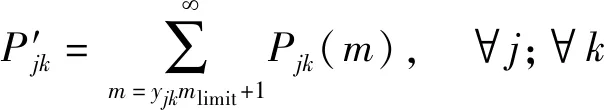
(5)

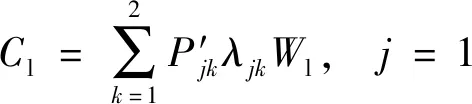
(6)

式中：Pjk(m)为方向j功能k中有m辆车的概率；mlimit为免费放行排队长度阈值，veh；P′jk为方向j功能k中超过免费放行长度yjmlimit的概率；Wl为平均每辆车通行费用，元/veh；Cl为收费站免费放行损失成本，元/h。

优化目标为运营成本、用户延误成本和收费站免费放行损失成本之和，即

min(CO+CT+Cl)

(7)

2.2 约束条件

2.2.1 车道划分约束

收费车道不能同时开放为出口和入口车道；为避免出入口车流相互交织，开放为出口的车道一定要位于出口侧，开放为入口的车道一定要位于入口侧；收费车道只有设计了各方向车道功能才能切换为此收费方向；各方向开放为各种功能车道数之和与切换为此方向的车道数相同；各方向开放为各种功能车道数不大于因车道设计限制允许开放的最大车道数。以上约束条件为

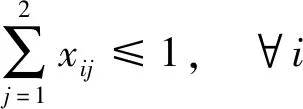
(8)

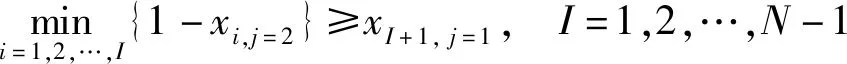
(9)

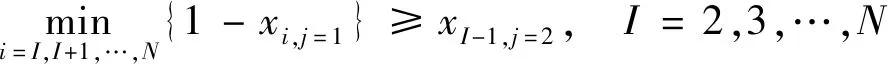
(10)

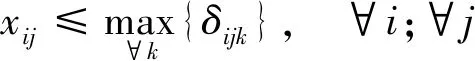
(11)

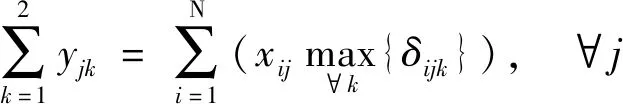
(12)

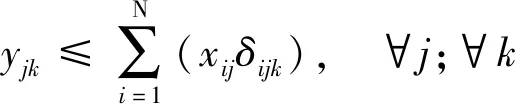
(13)

式中：xij为车道i是否切换为方向j，xij∈{0,1}，1表示是，0表示否；δijk为车道i是否可作为方向j功能k的收费车道，δijk∈{0,1}，1表示是，0表示否；根据收费车道具体设计输入；i为车道编号，以出口方向最右侧车道起往左分别编号{1,2,…,N}；N为收费广场所有车道数。

2.2.2 排队模型

采用数理统计中的M/M/N排队系统模型来描述车辆通过收费站的过程，即

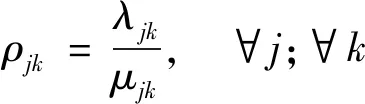
(14)

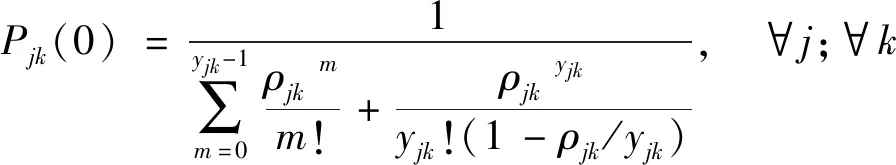
(15)

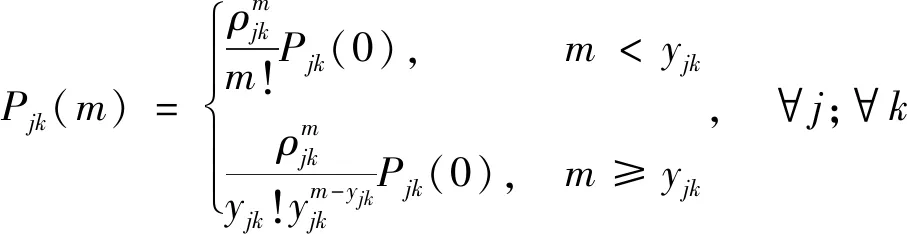
(16)

(17)

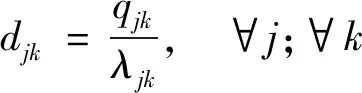
(18)

式中：ρjk为服务强度；qjk为平均排队长度，veh；μjk为平均服务率，veh/h。

根据级数求和公式推导将式(5)变为

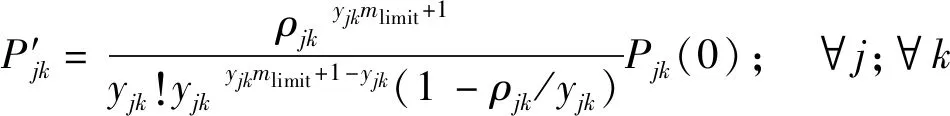
(19)

2.2.3 其他约束

为维持收费站稳定的运行状态，根据交通流理论中的排队论可知，每条车道的交通强度应小于1，及变量取值范围为

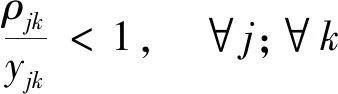
(20)

xij∈{0,1},yjk≥1,∀i;∀j;∀k

(21)

2.3 讨论

2.3.1 双向收费车道设置问题

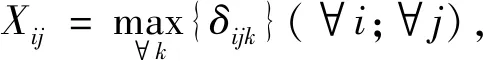
2.3.2 收费站免费放行判定标准

各省出台的收费站拥堵免费通行政策是对运营单位进行约束，避免运营单位为了降低运营成本，未开足收费车道，造成在用车道排队拥堵。为此，在交通强度为定值的情况下，据式(18)和式(19)，探讨不同开放车道数中免费放行排队长度阈值对免费放行概率和车辆平均等待时间的影响，如图2所示。

由图2可知，免费放行概率随免费放行排队长度阈值增加而降低，当阈值超过5～10 veh后，免费放行概率接近于零，此时阈值的增加对降低收费站免费放行损失成本作用较小，同时当阈值确定后，通过增加车道数，降低交通强度，可以降低免费放行概率，从而减少收费站免费放行损失成本。因平均等待时间随阈值增加而增加，为平衡收费站免费放行损失成本和用户延误成本，根据收费站车道数和管控目标，免费放行排队长度阈值宜在5～10 veh选取。

3 案例分析

3.1 基础参数

选取如图1所示的收费广场作为研究对象，该收费广场常规布局为出口方向7条车道，入口方向6条车道。为验证本文优化控制的通行效益，选取车道不可切换收费方向的控制方案(简称“传统方案”)对比分析。参考《收费公路联网收费技术要求》和林培群[4]等参数取值，选取如表1所示的输入参数。选取6种流量场景，根据优化模型确定收费广场的最优车道配置方案，结果如表2所示。

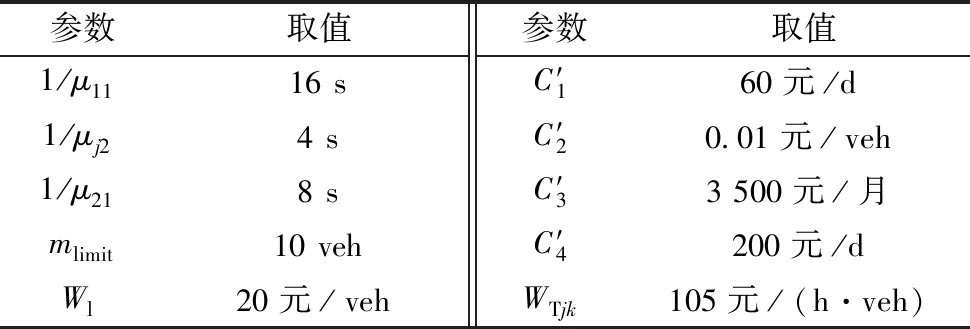
表1 基础参数Table 1 Basic parameters

3.2 结果分析

利用VISSIM 9.0软件对两种方案仿真对比分析，调整随机种子共仿真10次取均值作为评价依据[16]。如表3所示，在场景1、2中，两种方案成本指标和延误指标均相同，原因在于此时出入口交通需求较均衡，不需要切换车道方向便能达到系统最优。对于场景3、4出口交通需求大于入口，优化方案通过切换车道方向以分配更多的车道供出口使用，从而使得优化方案系统成本和总平均延误小于传统方案，提升了收费站通行效率。而场景5、6入口交通需求大于出口，优化方案则分配更多的车道供入口使用，以保证系统最优。由表2可知，因场景2、4、6车辆ETC使用率大于场景1、3、5，所以模型分配更多的车道作为ETC车道，同时降低了系统成本和总平均延误，说明增加ETC使用率，能显著提升收费站通行效率。

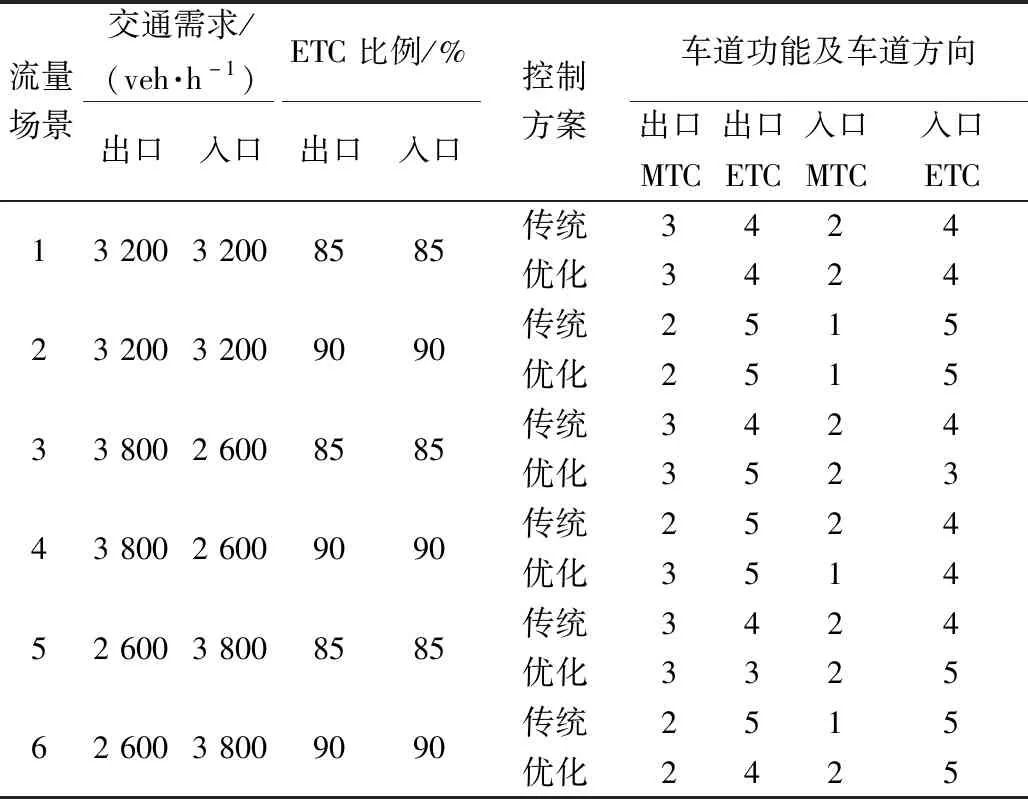
表2 不同情况下车道数的最优配置Table 2 Optimal allocation of lanes under different conditions

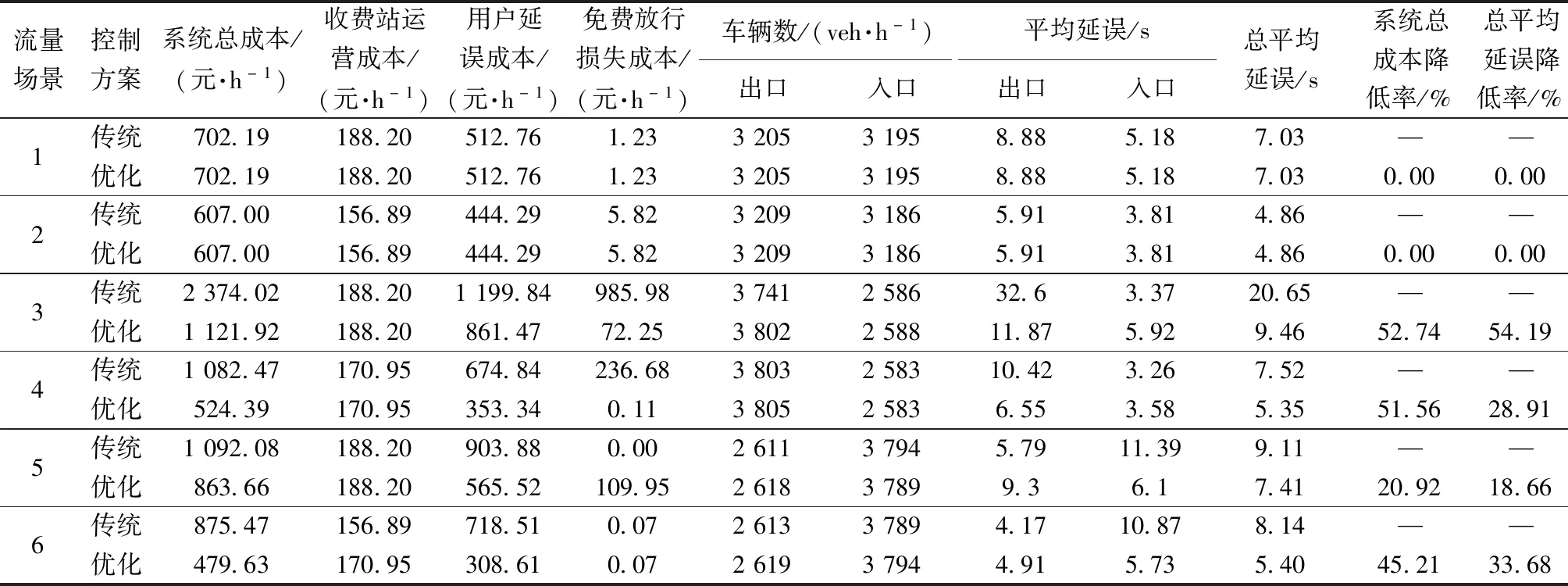
表3 仿真评价指标Table 3 Simulation evaluation indicators

4 敏感性分析

进一步分析两种方案适用场景，探讨ETC使用率和交通需求对系统成本的影响，ETC使用率取30%～90%，收费广场总交通需求取3 000～6 000 pcu/h，优化方案所有车道均设计为双向混合车道，传统方案所有车道均设计为单向混合车道，其余输入参数和案例分析相同。

如图3所示，系统成本随着ETC使用率增加而降低，且降低幅度逐渐减小，图3(b)存在不满足此规律的特例是由于决策变量为离散取值集合导致的。系统成本随交通需求的增加而增加，且当交通需求较大、MTC使用率较高时，收费站通行能力不能满足交通需求，使得模型没有可行解。整体来看，优化方案系统成本普遍小于传统方案，说明基于车道的收费站控制方法能够提升收费站通行效率。同时，在部分流量场景中，优化方案存在可行解，而传统方案不存在可行解，说明优化方案在不扩建收费站的前提下，通过车道控制突破了出口或者入口的容量限制，实现收费站“智慧扩容”。

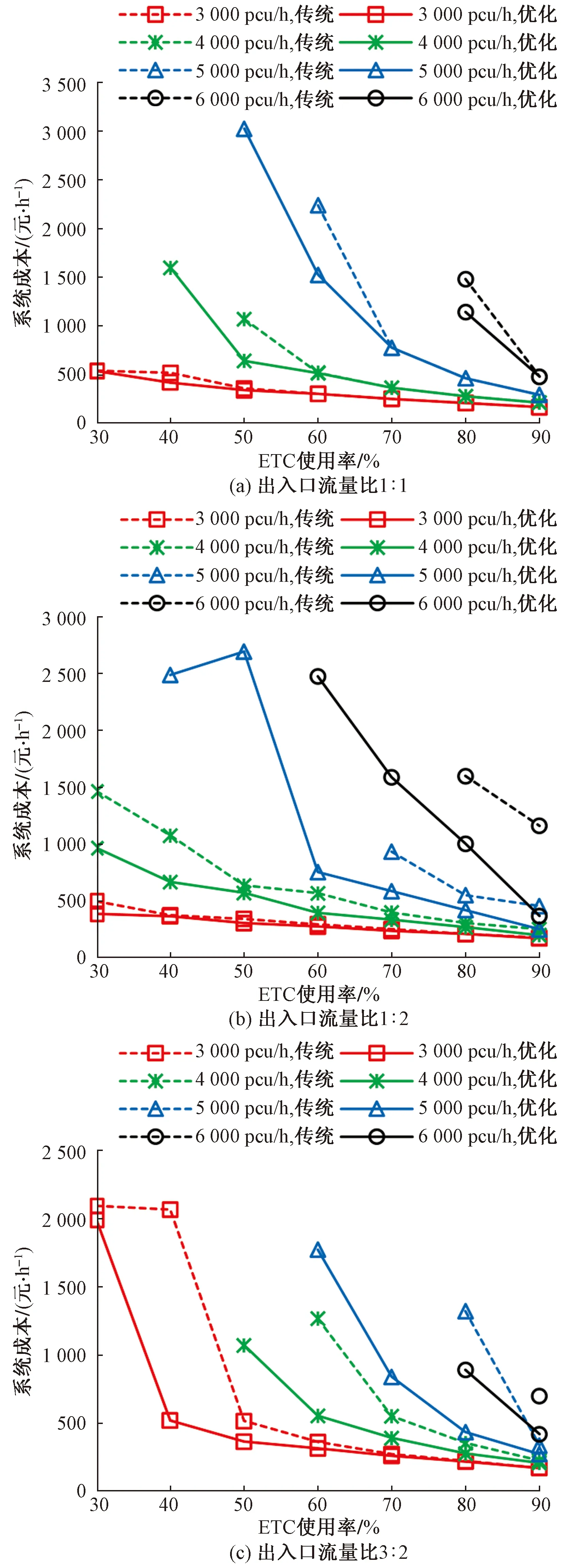
图3 ETC使用率、到达流量和系统成本关系Fig.3 Relationship between ETC usage rate,arrival flow rate and system cost

5 结论

(1) 通过动态调整收费车道使用功能和切换车道收费方向，构建了基于车道的收费站车道功能及收费方向优化模型。通过讨论发现：出口车道、入口车道需从各自行车方向的最右侧往左连续设置，使得在收费广场中间车道形成双向收费；收费站免费放行排队长度阈值宜在5～10 veh之间选取。

(2)通过案例分析和敏感性分析发现，优化方案通过动态调整车道方向和车道功能，以平衡出入口交通需求，降低了系统成本，提升了收费站通行效率。随着ETC使用率增加、交通需求减少，系统成本随之降低。优化方案系统成本普遍小于传统方案，且适用的流量场景更广。

(3) 在本文的后续研究中应重点关注中央分隔带位置调整、车辆变道等微观特征对收费车道通行能力的影响，以保证实际应用效果最佳。