基于修正证据理论的高耸结构翻模施工安全风险评估

桑莹雪,韩风霞*,乔亮,李占成,王守西

(1.新疆大学建筑工程学院，乌鲁木齐 830017；2.中铁二十一局集团第一工程有限公司，乌鲁木齐 830026)

近年来，高度发展的社会经济以及迅速的城镇化进程增加了高耸结构的数量，不论是公共建筑或者民用建筑，其设计都普遍采用框架、剪力墙或框剪结构。因此，模板工程在建筑主体结构施工中的重要意义也越来越突出。高耸结构随着施工高度的变化，外部风荷载等因素对施工的影响更是不容忽视，其施工具有较大的难度和一定的技术含量，使得施工过程的复杂性和不确定性等特点显著[1]。翻模施工是在传统爬模技术上进行了现代化的演变，其工艺和技术带有相对的特殊性，因能更好地适应多样化变截面施工近年来被广泛的应用于筒形、矩形等工程实际。但翻模相关的施工方案因结构体系复杂、涉及到的相关工艺较多、技术要求高，对其安全性的研究尚不完善，一旦发生翻模模板施工安全生产事故，将造成一定的损失，从而风险评估仍是施工安全监督管理的重要内容。目前对高耸结构翻模施工安全的研究成果日渐丰富，但大多仍是在施工技术层面上进行的，而从施工安全风险管理理论分析方面去阐述高耸结构翻模安全性的研究还不多见。基于对事故风险和重大安全影响因素的系统分析，有必要探索一种有效的高耸结构翻模施工安全风险评价方法，以降低其安全风险，推动高耸结构翻模的可持续发展。

目前，国内外学者针对建筑施工风险评价的方法进行了大量的研究，并在实际工程中得到了应用。如：Nguyen等[2]为解决建筑风险评估时缺乏历史数据和依赖专家意见的情况，首次基于改进的模糊集理论开发了模糊隶属度函数分步过程，以此确定风险变量；Li等[3]提出了建立云模型对基于层次分析法的风险评估方法进行了改进,并形成了基于云的层次分析法施工风险评估体系；张静萱等[4]则基于熵权和物元可拓模型，首次提出一种基于施工运营的安全评价方法。Solovyev等[5]在可靠性分析同时涉及定量和定性等不确定性的情况时，首次提出了一种基于证据理论和模糊概率分布相结合的结构可靠性分析方法。针对高耸结构翻模施工安全风险评价方面，López-Arquillos等[6]采用静态分组的方法，对模板施工的12个活动的安全风险进行评估，以此确定高空坠落为最危险的模板施工活动；王晶猛等[7]基于传统作业条件危险性评价法(LEC法)进行改进，对高大模板施工风险评估进行半定量化评估，得到模板风险事件的等级。

综上所见，大多数研究是针对建筑施工风险评估进行的，对高耸混凝土塔翻模施工风险评估的研究还不多。高耸混凝土塔翻模施工风险评估受诸多种因素影响，它们之间的关系是复杂的，在评价过程中常采用专家判断为指标权重的确定提供定量化依据，但这也容易产生对专家意见的依赖。此外，在高耸混凝土塔翻模施工安全风险评价中，专家的意见往往具有不一致性，以往的评价方法通常无法充分综合专家意见导致其评价结果具有不确定性。证据理论在不确定性处理和意见融合方面具有很高的有效性，使之可以应用于信息系统融合、风险评价等诸多领域。因此，现结合翻模施工工艺从模板安装、钢筋安设、混凝土浇筑、模板提升、模板拆除等5个方面构建评价指标体系，引入主观与客观相结合的结构熵权法对指标权重赋值，提高权重确定的科学性和准确性，运用贝叶斯修正的证据理论，处理不确定性信息并充分利用多源信息以得到更好的融合结果，提高对高耸混凝土塔翻模施工安全风险评估的准确性。

1 高耸结构翻模施工安全危险源分析

1.1 高耸结构施工安全威胁分类

高耸结构具备了建筑高度高、建筑材料需用量大、大型机械配合度高等特点，同时施工项目通常危险源多，其中不乏重大危险源出现。通过《住房和城乡建设部办公厅关于2019年房屋和市政工程生产安全较大及以上事故情况的通报》[8]可见，以土方和基坑开挖、模板支撑体系、建筑起重机械为代表的危险性较大的分部分项工程事故占总数的73.91%，依然是风险防控的重点和难点，具体描述见图1。

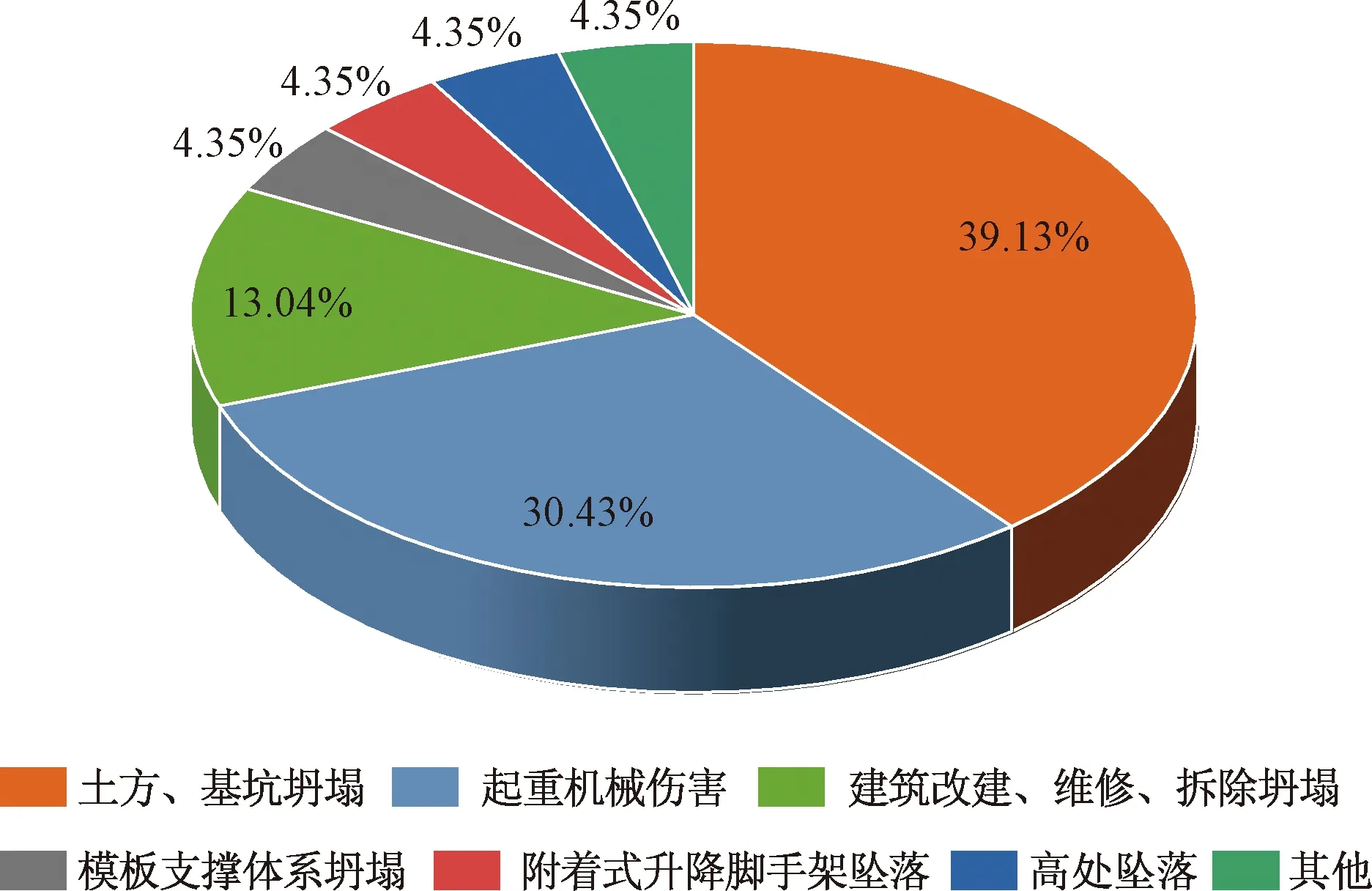
图1 2019年全国房屋市政工程安全生产较大及以上事故类型情况Fig.1 The national housing and municipal engineering safety production accidents of major and above types in 2019

1.2 高耸混凝土塔翻模施工安全需求

翻模施工技术是利用具有一定工作强度的混凝土结构作为固定支撑体，施工所需的各种材料用吊车或塔吊进行提升，上层模板支承在下层模板上，交替循环上升进行施工作业。虽然此项技术已趋于成熟并广泛应用于高耸结构建设项目中，但与其配套的施工工作平台及安全防护措施由于缺乏统一的标准和规范，使得工程质量和施工安全难以充分保证。同时对施工过程中存在的诸如风荷载等偶然因素的考虑往往容易忽略，从而带来较大安全隐患。因此对施工过程中可能存在的风险源进行识别、预估、响应和分析，以确保施工安全是必要的。

2 构建评价指标体系的因素选择

本文从翻模施工技术及工艺角度出发，结合大量工程实践和众多专家研究，参照中国已发布并实施的《建筑施工模板安全技术规范》(JGJ 162—2008)、《施工企业安全生产管理规范》(GB 50656—2011)、《混凝土结构工程施工规范》(GB 50666—2011)等，针对高耸混凝土塔翻模施工安全风险评估这一目标，从模板安装、钢筋搭设、混凝土浇筑、模板提升、模板拆除5方面[9]进行论述，最后确立了高耸混凝土塔翻模施工安全风险指标体系，见表1。

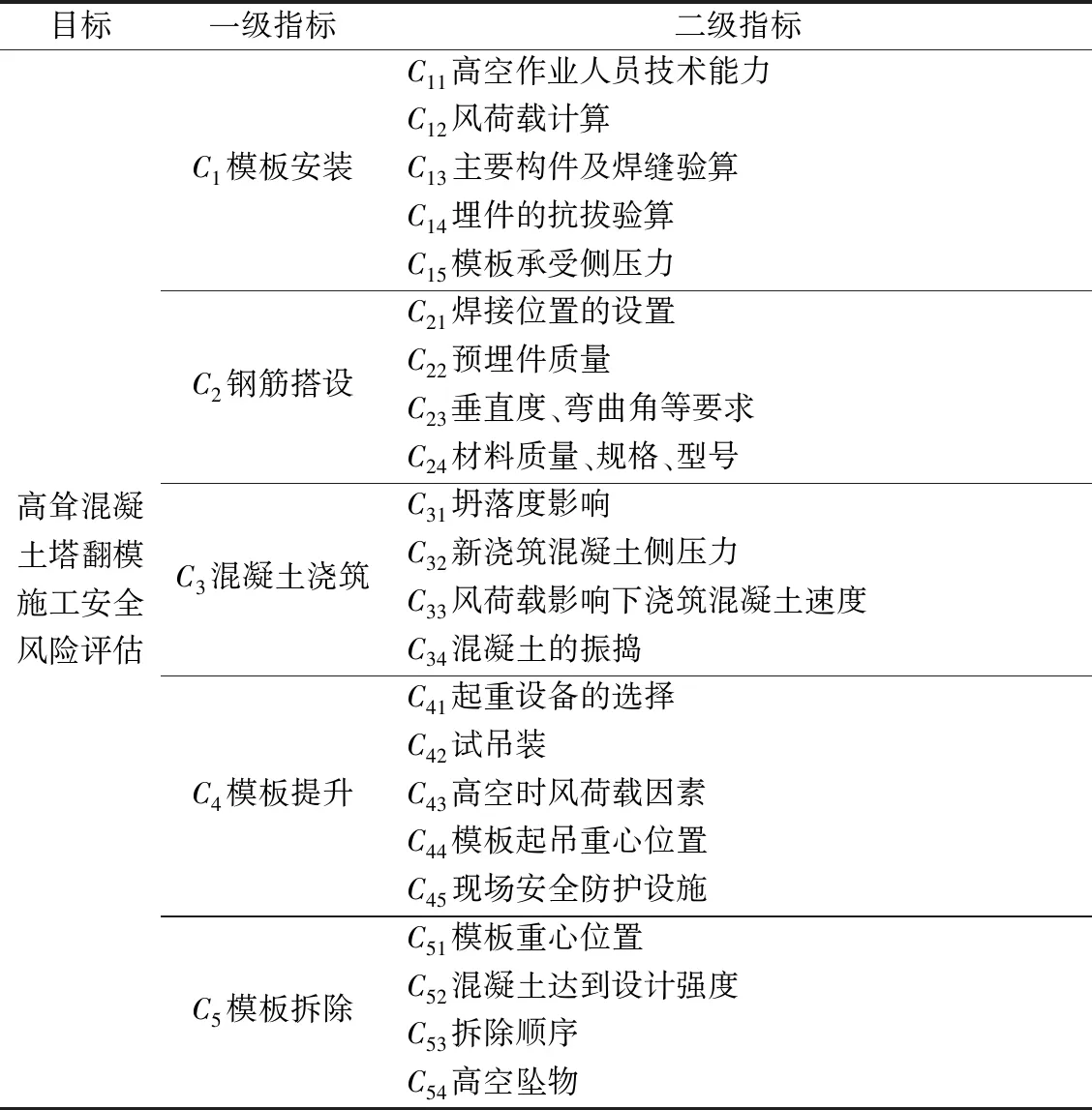
表1 高耸结构模板施工安全风险评估指标体系Table 1 Safety risk evaluation index system of high-rise building formwork construction

3 基于结构熵权法的评价指标权重计算

施工安全风险评价是一个要综合考虑基于风险评价体系中多个指标，并将其定量化的分析过程，因此保证指标权重的合理性是十分重要的。目前，指标权重的计算方法可分为主观赋值和客观赋值两类。在主观分配中专家的经验可以得到充分利用[10]，同时专家个人的学识和目的差异往往使结果呈现出较大波动；客观分配在一般情形下精度比较好，但是容易因为筛选客观数据时忽略其代表的意义出现与现实不符的状况。为最大限度的发挥主观性和客观赋权的精确性，本文中采用主观德尔菲法与客观熵值法相结合的方式来判断指标的权重大小。结构熵权法计算指标权重大小的具体过程[11]为

(1)专家意见征集。假设有k组专家，则第i组专家表示为Ei。然后每组专家根据他们的专业知识和经验对所有安全指数C=(c1,c2,…,cn)进行重要性排列。评价指数根据其重要性从高到低进行排名，例如，标记“1”表示“最重要”，标记“2”表示“第二重要”，等等。在此过程中，专家的选择应具有代表性、权威性和公平性。可以允许一些指标被认定为同样重要，指标的最终排名可经过所有专家的讨论得出。专家Ei对指标ci的评价指数为aij，由此可得出代表专业人员意见的典型排序矩阵,记作

i=1,2,…,k;j=1,2,…,n。

(1)

(2)确定结构熵[12]的重要性矩阵。典型排序矩阵通常具有来自专家意见的数据“噪声”，这可能会导致偏差和不确定性。为了消除这种数据“噪声”并减小不确定性，需要对典型排序矩阵A代表的专家意见进行统计分析。以下使用熵理论计算熵值，其定性排名结果可以通过隶属函数转换为定量结果，隶属函数χ(I)定义为

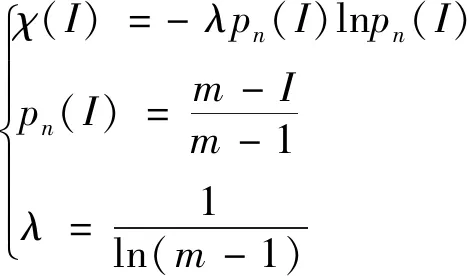
(2)

式(2)中：I为专家组对指标的排序数值；m为转换参数，假定m=j+2，则j对应的为序号中的最大值。

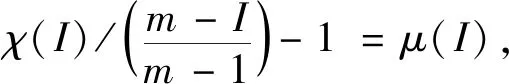
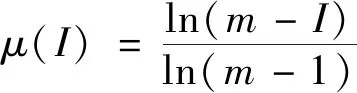
(3)

(3)将典型排序矩阵A中每个I=aij代入式(3)，对aij进行定量转换，令c(aij)=bij，由此可求得排序数I的隶属度矩阵B[B=(bij)k×n,i=1,2,…,k;j=1,2,…,n]。

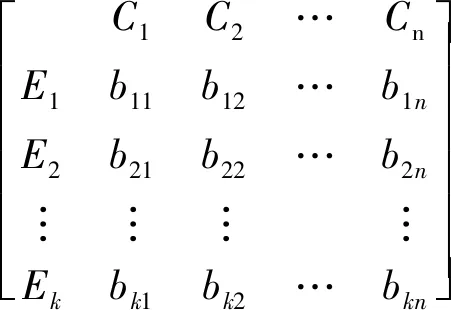
(4)

(4)消除认识盲度。不同领域方向的专家对于同一个问题的看法存在一些理解差异，这就是认识盲度，增加了分析问题的不确定性。

对数组{b1j,b2j,…,bkj}取算术平均值,记作bj，表达式为

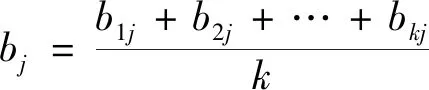
(5)

称bj为k个专家对指标cj的一致认识，也叫作平均认识度。

定义专家对指标cj的认识差异为认识盲度Qj，表达式为

Qj=|[max(b1j,b2j,…,bkj)-bj]+

[bj-min(b1j,b2j,…,bkj)]/2|

(6)

由此所有专家对指标cj的整体认识程度xj定义为

xj=bj(1-Qj)

(7)

最后，可根据指标cj的整体认识度xj而得到评价向量X=(x1,x2,…,xn)，再进行归一化后的指标综合权重，表达式为

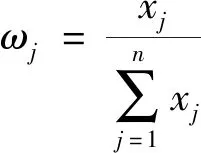
(8)

4 基于修正证据理论的证据合成

在施工风险评估过程中，考虑到选定的指标并不能完全代表施工安全所有影响因素以及专家评价产生的差异，因此，将使用修正证据理论的方法对结构翻模工程施工过程做出安全风险评估。证据理论可以逐步缩小较少信息蕴含的不确定性，最终得到具有一定可信度的结果。通过修正证据理论的方法能够对结构模板工程施工安全风险评价中可能具有包容性的不确定性问题进行科学有效的解释，并且能够很好地解决不同专家看法中的冲突问题。

4.1 证据理论的概念

证据理论是由Dempster[13]首次提出的一种描述不确定性问题的方法，通过定义辨识框架Θ和信度函数，可以把关注的命题描述为建立在辨识框架基础上的各个子集，并由具有上下限的可信度函数值(信度区间)来表明其发生可能性，进而依靠多个证据的积累融合来减小推断的不确定性。辨识框架Θ是一个非空集合，由一些相互互斥的基本子集构成。每个命题都相对于在辨识框架Θ上的某个子集合，并满足关系式

(9)

式(9)中：m:2Θ→[0,1]为Θ上的基本可信度赋值，即mass函数；2Θ表示Θ中所有子集所组成集合，包括2n个元素，n为集合Θ中两两互斥的子集数量。对于辨识框架Θ中的命题(或事件)A，m(A)表示根据证据m，A事件所发生的可能性。如果m(A)>0，则称A为一个焦元(focal element)，并定义信任函数(Bel)和似真函数(Pl)来描述命题A发生概率的取值范围，表达式为

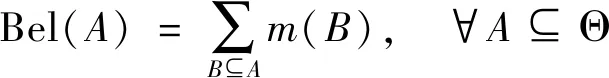
(10)

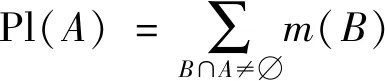
(11)

4.2 证据理论中的数据来源

以结构模板工程施工的安全风险为主要评价目标，将评价目标细分成n个一级评价指标Ci(C1,C2,…,Cn)，并在此基础上，将一级评价指标再细分为二级评价指标Cij(i=1,2,…,n;j=1,2,…,k)，从而形成了多层次的评估指标体系。

在证据理论中，评判准则通常分为高、中、低等若干个评判层次，评语的集合定义为Θ={θ1,θ2,θ3,…}，其中θk(k=1,2,3，…)作为指标Ci可能被判定的一个评语。专家对指标评语的支持率即指标Ci被判定为θk的概率，记为βik。例如10位专家中的2位专家认为指标Ci属于评价标准中的θk，即Ci被判定为θk的概率βik=0.2。由此，得到评价矩阵D为

(12)

4.3 mass函数计算

在mass函数[14]计算时，通常引入折扣率a(0≤a≤l)来反映决策者对指标评价结果不能完全接受的实际，一般取a=0.9。

由以下过程得到mass函数矩阵：第一，将结构熵权法所定义的指标权重向量中，权重最高的指标定为关键指标。对于关键指标Ci，设其被评价为θj(j=1,2,…,k)的概率为βij；考虑到决策人员对这一结论的信任程度，可以对定义关键指标的信任程度值为mij=aβij；而对非关键指标Cq来说，设其对θj(j=1,2,…,k)的概率为βqj，根据Cq对关键指标Ci的重要程度wq/wi，可定义其折扣率为(wq/wi)/a，其信任程度为mqj=(wq/wi)/(aβqj)。

对任一级指标Ci，其基本信度函数值为

mi(θj)=mij，i=1，2，…，n;j=1，2，…，k

(13)

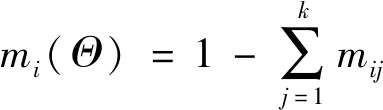
(14)

式中：mij表示第i个指标被确定为等级θj的概率,而mi(Θ)则代表第i个指标的不确定程度，是未被分配的概率。

由此生成与之相应的n个指标的mass函数矩阵，即

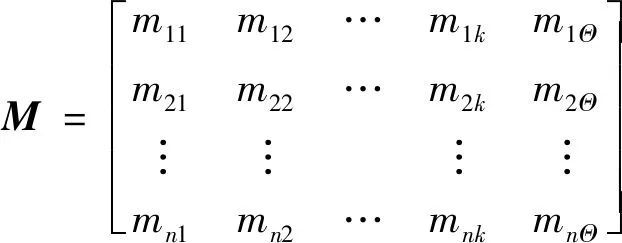
(15)

4.4 证据理论的组合规则

取得基本概率赋值后，运用证据理论中的Dempster证据合成规则将证据进行融合计算，定义如下。

对于∀⊆Θ，Θ中的两个mass函数m1、m2合成后的基本概率赋值为

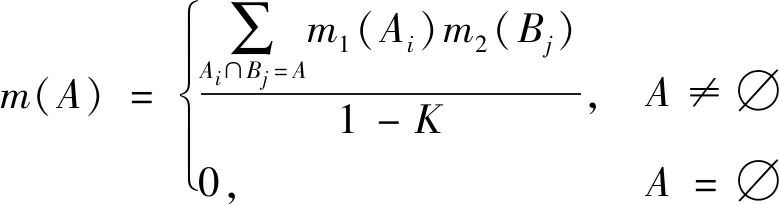
(16)

考虑到对多指标的mass函数矩阵，Dempster证据合成过程计算量过大，n个评估指标就有2n-1个“焦元”。为了避免上述“焦元爆炸”问题，简化焦元数目以减小计算量，在不影响合成结果的前提下，本文中采用Voorbraak F提出的Bayes简化公式进行计算[15]。Bayes简化计算公式为

m(A)=

(17)

式(17)中：C为构成辨识框架集合Θ的子集，|C|为集合C的子集个数。

最后，将修正的mass函数值代入式(16)，便得到修正后的证据合成公式。修正后的证据合成公式具有更好的收敛性，能够有效提高高耸建筑施工风险评估结果的聚焦程度，从而提高评价结果的可靠性。

5 实证研究

选用新疆某工程作为实例进行实证分析，该工程结构形式为钢筋混凝土圆筒形塔结构，建筑高度149.85 m，地上28层，地下2层。结构半径10.5 m，每层梁板支架的跨度均大于18 m。墙身外模采用悬臂式翻模，模板尺寸为5.6 m×4.131 m(高×宽)。模板平面和立面布置图分别见图2。采用本文建立的基于结构熵权和修正证据理论的评价方法，对该工程施工过程的翻模模板体系进行安全风险评估。

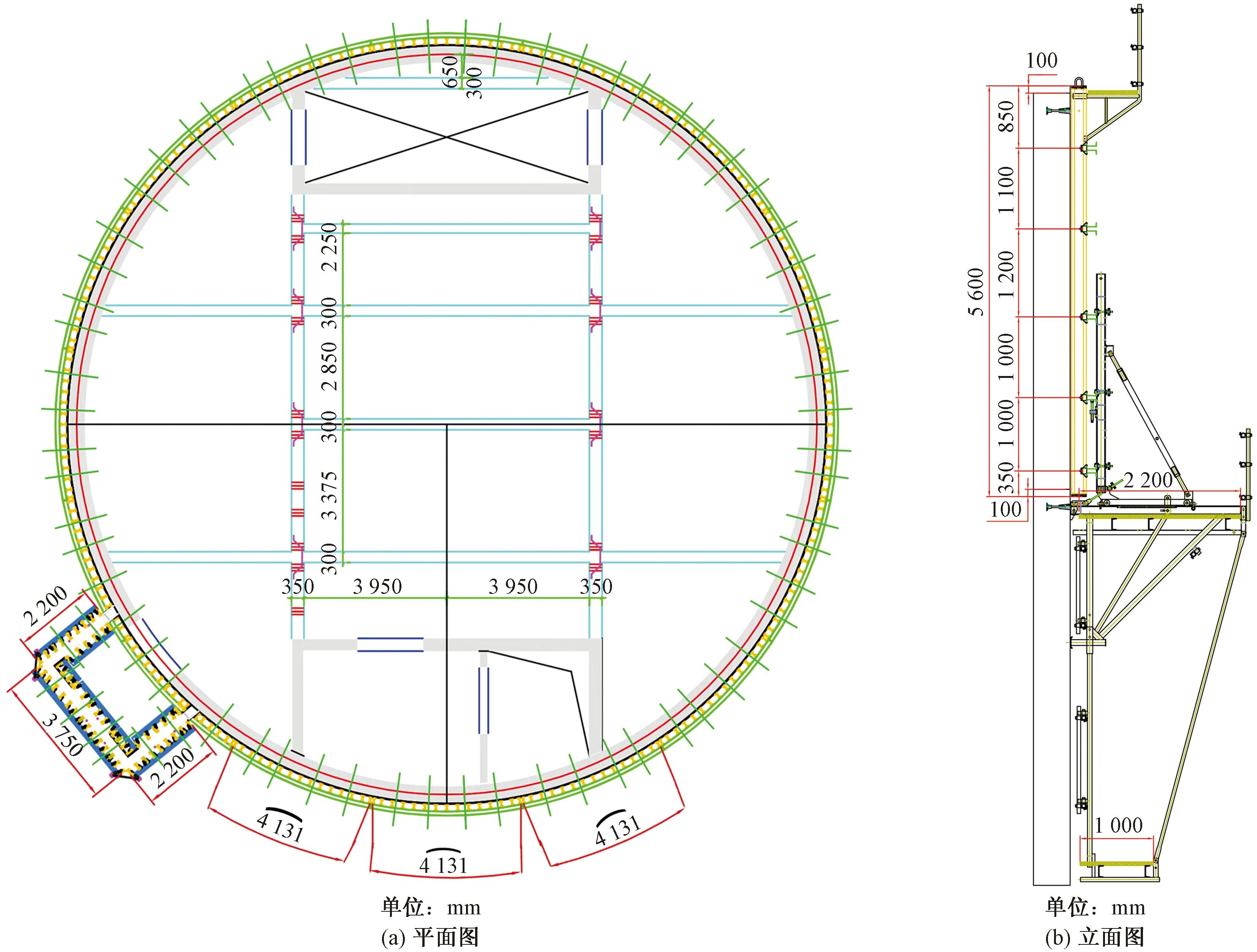
图2 模板布置图Fig.2 Formwork layout

5.1 确定指标权重

运用结构熵权法计算高耸结构模板施工安全风险评价指标体系中各级指标的权重值。将以下5个一级指标作为例子，具体介绍指标权重的确定过程。

(1)专家意见征集，形成了典型排序矩阵。邀请在高耸建筑模板现场施工及风险管控方面具备大量成功经验的专家，合计15人，将他们随机分为5组，3人为一组。每组专家对各个指标的重要性进行独立排序，在进行若干次的反馈和讨论之后，根据结论形成了由5组专家共同讨论之后的典型排序矩阵(aij)5×5，展开式为

(18)

(2)应用熵理论计算熵值，并进行盲度分析，计算总体认识度。将定性排名结果形成的典型排序矩阵aij利用式(3)，转换为定量矩阵(bij)5×5，即

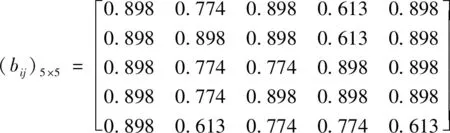
(19)

依照式(5)～式(7)可以计算得到5组专家的整体认识度，记作X，为

X=(0.898,0.657,0.796,0.651,0.721)

(20)

(3)通过应用式(8)对X进行归一化处理，得出的就是5个一级指标的综合权重。该向量代表了专家们对各指标重要性的一致性评估。

w=(0.241,0.177,0.214,0.175,0.194)

(21)

按照上述相同的方法计算的二级指标权重见表2。

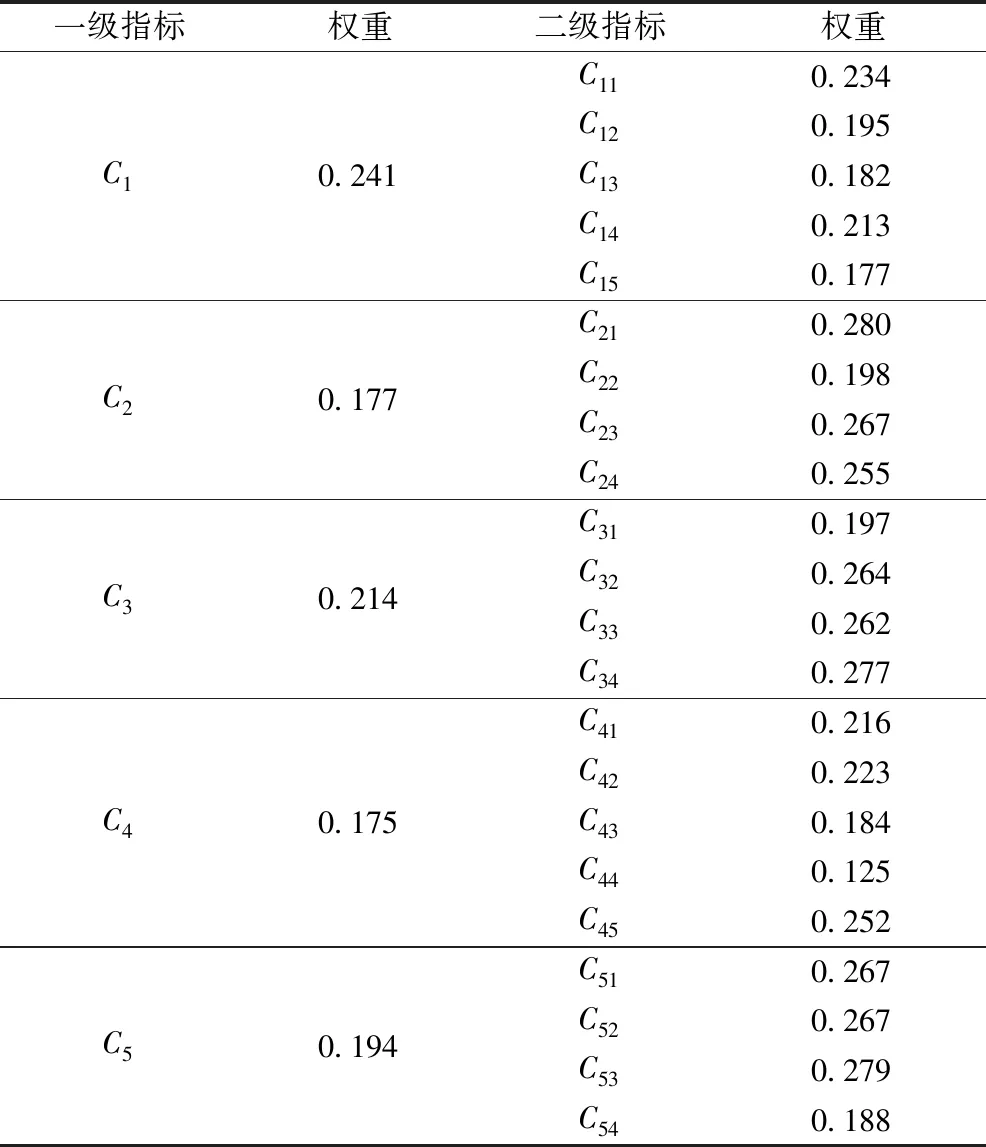
表2 模板施工各级风险评价指标权重Table 2 Formwork construction risk evaluation index weight at all levels

5.2 基于证据理论的评价过程

5.2.1 确立证据来源数据

将高耸结构翻模施工技术的施工安全风险分为高、较高、中等、低、较低5个层级，用θ1、θ2、θ3、θ4、θ5表示，由它们组成的集合为辨识框架，即Θ={θ1、θ2、θ3、θ4、θ5}。

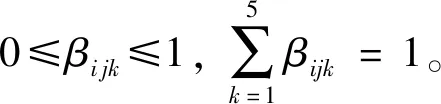
5.2.2 mass函数的融合计算

将影响高耸结构翻模施工安全风险评价中的各指标作为证据理论中证据，评价等级Θ={θ1、θ2、θ3、θ4、θ5}作为识别框架，结合表3辨别框架Θ中的基本支持度数值，构建mass函数。

以C1为例具体分析，C1的指标权重向量w1={w11,w12,w13,w14,w15}=(0.234,0.195,0.182,0.213,0.177)，可见，C11为关键指标。依据mass函数的计算规则，对C11折扣率取a=0.9，则C12、C13、C14、C15折扣率分别为(w12/w11)a=0.750、(w13/w11)a= 0.701、(w14/w11)a=0.821、(w15/w11)a=0.680。参照表3中C1评价指标的基本支持度，可得到C1的mass函数矩阵为

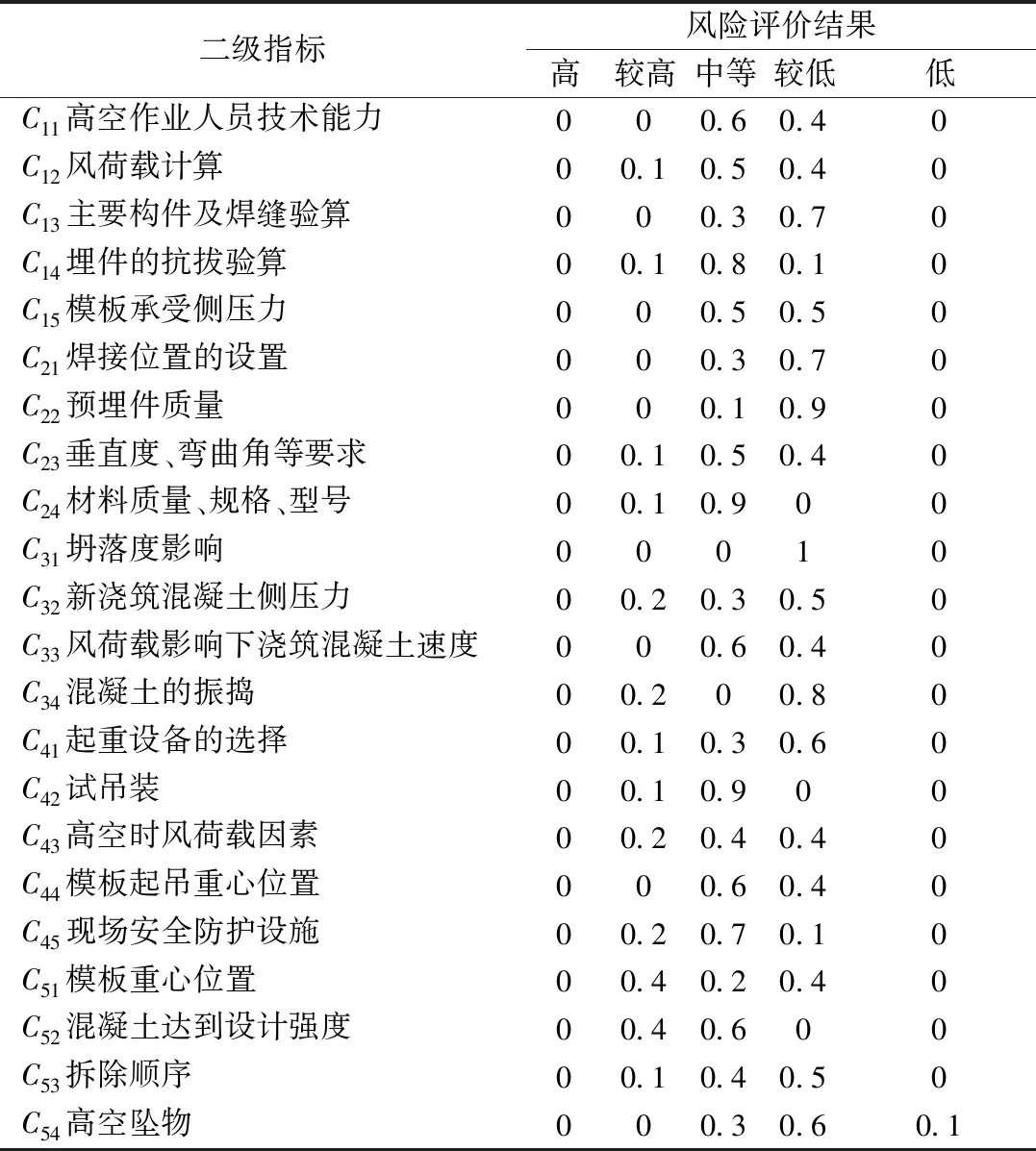
表3 专家对各二级指标风险评价结果Table 3 Expert risk evaluation results for each secondary index

M(C1)=

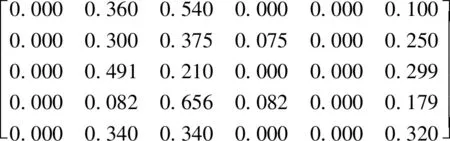
(22)

根据式(17)对原mass函数加以Bayes近似计算，并用Bayes近似计算值取代mass函数值，从而得出经过修正的mass函数为

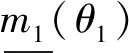
=0.071

(23)

同样的，分别可以计算出

由此可得到C1的修正mass函数矩阵为

(24)

5.2.3 Dempster证据合成

根据式(16)在经过三次递归合成后，将C1中包含的5个二级指标的修正mass函数合成为一个mass函数。其第一次递归合成结果为{0.034,0.344,0.544,0.044,0.034}；第二次递归合成结果为{0.017,0.467,0.476,0.023,0.017}；第三次递归合成结果为{0.006,0.229,0.748,0.011,0.006}；第四次递归合成的最后结果为{0.003,0.232,0.757,0.005,0.003}。同样的计算C2、C3、C4、C5的最后合成结果。由上述得到的5个一级指标的递归合成结果，建立一级指标的评价矩阵为

(25)

5.2.4 综合评价值的计算

通过一级指标权重向量w=(w1,w2,w3,w4,w5)= (0.241,0.177,0.214,0.175,0.194)，可知C1为关键指标，则可以按照标准mass函数的计算方法，取C1折扣率a=0.9，即C2、C3、C4、C5的折扣率分别为0.659、0.797、0.652、0.723，则评价目标的mass函数就可以用矩阵描述为

M(C)=

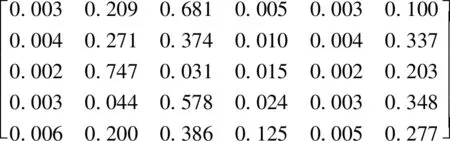
(26)

通过式(10)得到修正后的mass函数矩阵为

(27)

同理，依据前述递归合成算法，对修正后的mass函数矩阵进行4次递归合成后，得到最终的关于评价目标的合成结果：mC(θ1)=0.006，mC(θ2)=0.289，mC(θ3)=0.688，mC(θ4)=0.010，mC(θ5)=0.005。

5.3 评价结果分析

根据上述计算结果，对五个一级指标递归合成后形成的结果(见图3)，进行分析，风险等级高、较高、中等、较低、低的总体支持度分别为0.006、0.289、0.688、0.010和0.005，高、较低、低的递归合成结果分别接近0。按照隶属度最大的原则，从施工安全风险的角度评价高耸混凝土塔翻模施工安全属于总体可控的等级。同样，对模板安装、钢筋搭设、模板提升、模板拆除等因素的评价也属于中等，而混凝土浇筑因素的隶属度评价为“较高”。

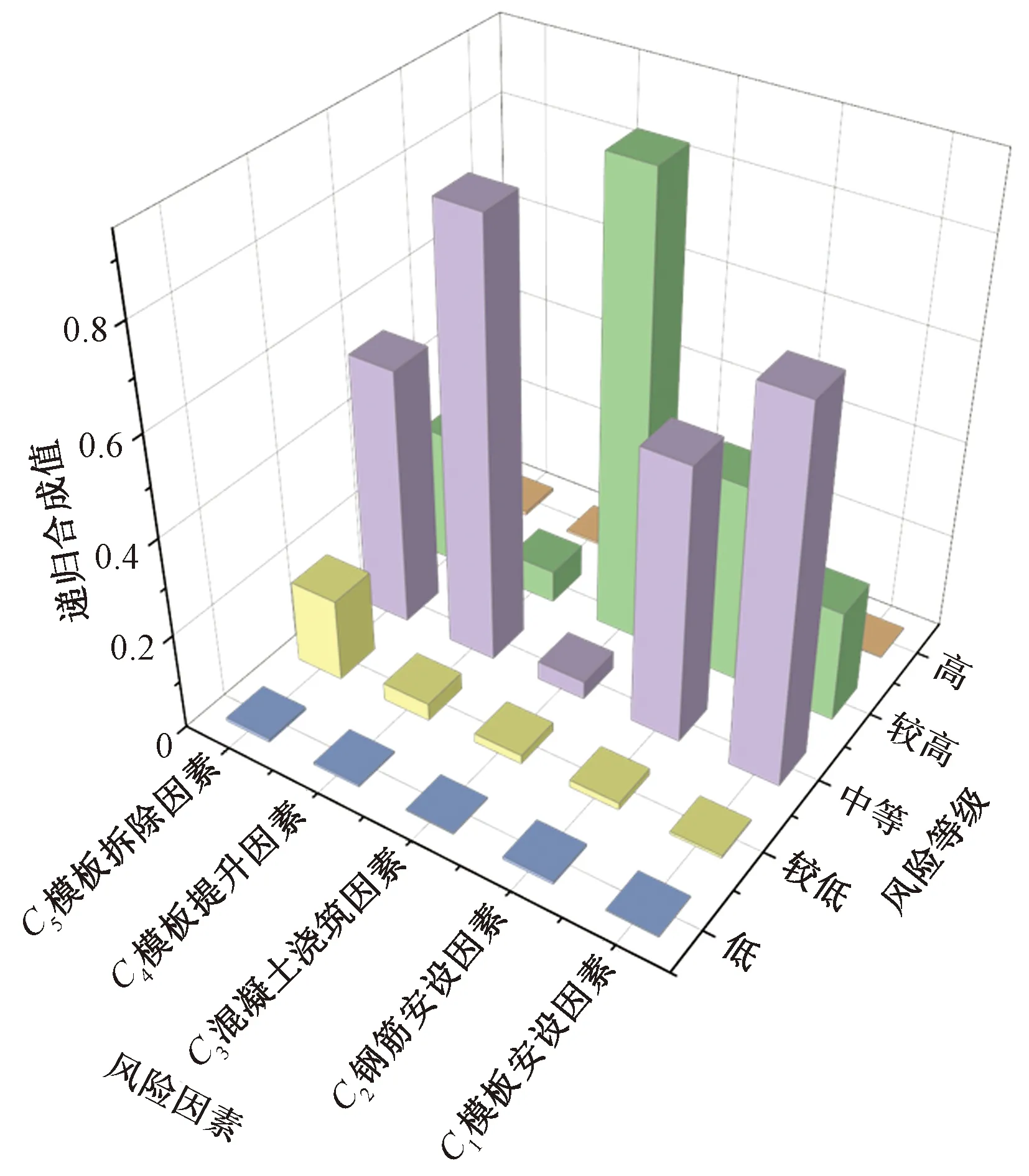
图3 一级指标递归合成结果Fig.3 Recursive synthesis results of first-level indicators

其中，C1模板安装因素的Dempster递归合成结果为{0.003,0.232,0.757,0.005,0.003}，从数据合成的结果来看，模板安设因素是构成施工安全风险的重要组成之一。首先操作人员的技术能力的提高会主动降低安全事故发生的概率，在模板设计时应充分考虑项目所在地区自然气候特点，适当提高设计安全冗余度，时刻将安全生产放在第一位。

C2钢筋搭设因素的Dempster递归合成结果为{0.006,0.412,0.567,0.015,0.006}，表明在安全风险评估体系中风险等级为中等，建议做好钢筋材料、规格及型号的比对工作，同时焊接位置的选择将会对下一步混凝土浇筑施工产生重要的影响，应当在施工中对不利的焊接位置加以避免。

C3混凝土浇筑因素的Dempster递归合成结果为{0.003,0.937,0.039,0.019,0.003}，隶属度最大的等级为较高，表明在高耸结构翻模施工安全的风险评估中，混凝土浇筑因素的带来的施工风险不可忽视，同时这与该项目实际情况相符。在施工中新浇筑混凝土时受到自然环境中风荷载以及大温差等因素的影响尤为显著，应做好风险预判和排查。

C4模板提升因素的Dempster递归合成结果为{0.005,0.068,0.885,0.036,0.005}，在高耸结构翻模施工风险评估体系的结果为中等，实际施工中模板提升过程确实存在一定的风险，既要重视外部风险因素的出现，也要做好安全防护工作以防高空物体打击的伤害。

C5模板拆除因素的Dempster递归合成结果为{0.009,0.277,0.534,0.172,0.007}，隶属于的评价结果为中等，在施工过程中混凝土强度必须达到规范要求后再拆除模板，并防止模板重心失稳带来的高空坠物危害，要重视拆除时的风险的管控，一旦忽视风险将有向“较高”程度发展的趋势。

根据最终一级指标的合成结果可见mC(θ3)>mC(θ2)>mC(θ4)>mC(θ1)>mC(θ5)，其中高、低风险等级的支持度分别接近0，根据最大隶属度原则，从施工安全的角度评价翻模施工的风险为中等，反映出在实际的施工过程中要重视各个施工阶段风险的识别，特别是在模板安装阶段以及混凝土浇筑阶段，要做出行之有效的风险应对预案。

5.4 有效性分析

在进行风险评价的过程中，可选用多种不确定理论建立风险评估模型，基于本文构建的施工风险评估模型对文献[16]的工程实例进行分析，以文献中构建的风险指标体系为例，采用贝叶斯修正证据理论对其权重进行递归合成，得到的合成结果为mC(θ4)>mC(θ3)>mC(θ5)>mC(θ2)>mC(θ1)，得到的风险评估结果按最大隶属度原则属于较低等级，与文献[16]中所采用的方法评价结果一致，见表4。因此，采用本文修正的合成规则进行数据融合能有效反应风险评估结果的有效性。

表4 两种评估方法的结果Table 4 Results of the two assessment methods

6 结论与建议

(1)结合高耸结构翻模施工的施工特点及关键工序的情况，从模板安装、钢筋搭设、混凝土浇筑、模板提升、模板拆除五方面确定了评价指标，引入结构熵权法，通过专家意见征集、盲度分析和归一化处理确定合理的指标权重，信息熵的运用提高了描述信息不确定性的能力。

(2)通过将贝叶斯近似法与专家意见相融合，解决了传统数据分析在处理评价指标之间不一致性，并能有效提高对不确定性问题评估的准确性。

(3)通过对某实际工程高耸结构翻模体系的施工进行安全实证研究与评价，评价结果中高耸结构翻模施工安全风险为“中等”，这与实际施工情况具有一致性，说明运用本文提出的评估方法具有一定的指导性和可操作性，为更精准的评价高耸结构翻模施工技术的安全风险提供了方法和参考。

由于各评价指标的安全风险等级的划分标准以及评价指标的分值是否合理会对评价结果产生较大影响。因此，在后续研究中，有必要进一步补充和完善高耸结构翻模施工安全风险评价指标，研究评价指标的分值及其安全风险分类标准，以进一步提高评价指标体系的科学性，增强评价结果的全面性和客观性。