2023年云南省初中学业水平考试数学试题分析与备考建议

王学先 董丽娥

2023年云南省初中学业水平考试虽然已经结束，但是对于新一批九年级备考的学生和教师而言这仅仅只是个开始.研究2023年初中学业水平考试试题，可以增强备考的科学性和有效性，提高备考效率.深入研究2023年初中学业水平考试的新变化，以研促教，优化复习策略，打造高效课堂，备战2024，是摆在全体九年级教师面前的首要问题.

一、试题的整体情况分析

2023年云南省初中学业水平考试数学试题更加注重考查基础，面向全体，弱化区分，充分体现义务教育阶段的要求，在《义务教育数学课程标准》（2022年版）（以下简称“新课标”）和“双减”“双升”政策，以及云南省新中考背景下，严格落实新课标命题的规定要求，减轻学生过重课业负担，坚持以学定考，以评促学，以评促教.试题回归教材，在注重考查“四基”“四能”和通性通法的同时，增加综合性、开放性、应用型、探究性试题的比例，直击学科核心素养，强化对数学本质的考查，减少机械记忆性试题，防止偏题、怪题，防止难度过大，切实提高命题质量，体现了以下变化点：

1.整体相对稳定，局部持续调整

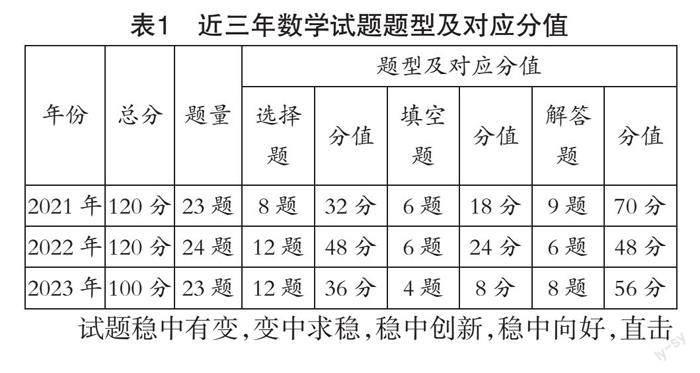
近三年云南省初中学业水平考试数学试题结构包括填空题、选择题、解答题三个大题，总体结构无变化，但这三年数学试卷每部分的题量和分值进行了微调.2023年数学试题满分由原来的120分调整为100分，具体情况见表1.

表1 近三年数学试题题型及对应分值

试题稳中有变，变中求稳，稳中创新，稳中向好，直击数学核心素养，有利于学生数学能力的提高，为学生的“学”指明有意义的方向，为教师的“教”指明有价值的导向，稳步提升质量.数学试题落实“双减”政策的要求，既让学生轻松快乐地学习，又能考出满意的答卷.随着新课标、新课程、新教材的落地和实施，2024年以后的试题结构还可能会进一步调整.

2.考查内容全面，占比趋于合理

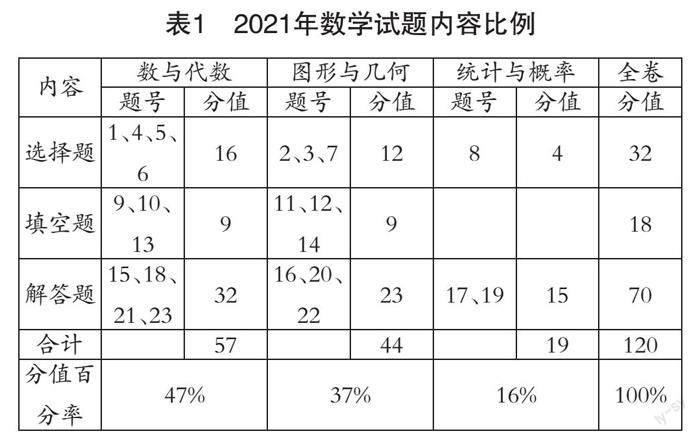
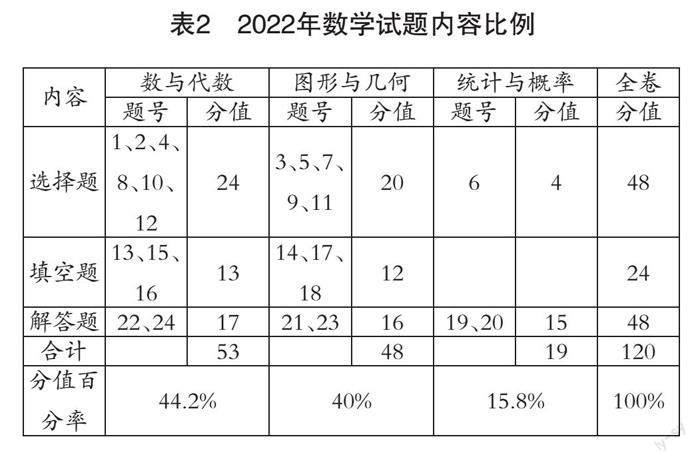
从考查内容上来看，近三年的云南省初中学业水平考试数学试题中包括数与代数、空间与图形、概率与统计三个部分的内容，保持既源于课本，又高于课本的特点，公正、客观、全面、准确地评价学生通过初中教育阶段的数学学习所获得的发展状况.表2、表3、表4是近三年云南省初中学业水平考试数学试题内容比例统计.

表1 2021年数学试题内容比例

表2 2022年数学试题内容比例

表3 2023年数学试题内容比例

总体上看，近三年数学试题考查内容占比总体相对稳定，并且逐步趋向合理.如表3，2023年的初中学业水平考试数学试题覆盖面广，考查数与代数、图形与几何、统计与概率三个领域的内容分值分别是43分、40分和17分，占比为43%、40%和17%，这与整个初中阶段数学知识在三个领域的课时比例吻合度极高.

3.分值设置清晰，难度结构明确

2023年云南省初中学业水平考试数学试题的多维细目表分值设置非常清晰.整套试卷难易度（易、中、难）比例为7∶2∶1，其中前20道题为简单题，共计70分，选择题和填空题中均不再命制压轴型的题目.以往的选择题最后一题综合性极高，常以含参不等式、含参分式等综合问题压轴;以往的填空题最后一题基本上是基于分类讨论思想的多解题，常以图形形状不确定、点位置不确定、运动方向不确定、对应关系不确定等问题压轴.如2021年填空题第14题（填空题最后一题）考查了正方形、等腰三角形性质及应用，涉及角平分线、勾股定理、锐角三角函数等知识.题目中没有给出图形，由于图形的不确定，故需要分类讨论，共有四种结果，属于难度高的试题.2022年填空题第18题（填空题最后一题）考查了等腰三角形的基本性质，由于给出的角度没有明确是等腰三角形的底角还是顶角，故需要分两种类型来讨论，属于简单的考查分类讨论思想的试题.而2023年填空题的最后一题，与往年相比，变化最大的是不再以双解（多解）的形式出现.从2023年考试的结果来看，考查的内容较为简单，此位置也不再考查分类讨论的思想，而对分类讨论思想的考查转移到解答题最后一题来体现.明显的变化是填空题多解的淡化和分类讨论思想的转移.对解答题而言，2023年的第17题分值6分，主要考查实数运算;第18题分值6分，主要考查全等三角形的判定和性质;第19、20题分值均为7分，分别考查统计和概率的知识;第21、22题分值均为7分，主要考查“图形与几何”中的四边形和“数与代数”中的一次函数、不等式或方程的知识，并且每道题都按中等难度要求设置;第23、24题分值均为8分，属于压轴题，主要考查图形与几何中的圆和数与代数中的二次函数的知识，并且每道题第一问按中等难度设置，分值为3分，第二问按较高难度设置，分值为5分，对于学生而言，最后两道试题的最后一问难度很大，年年有创新，不易得高分.总之，试题题型结构、分值设置、难度结构、内容结构均已做到清晰明确，泾渭分明.

二、新课标理念下的命题趋势分析

1.依据课标理念，立足全国视野

从2023年全国各地的初中学业水平考试数学试题来看，随着新课标的颁布和实施，核心素养、跨学科、大单元等概念走进了今天的数学课堂.学业水平考试在尊重课程标准、尊重学生的基础上，在命题风格、命题素材等方面做了一些改进和创新，既要考查基础知识、基本技能，也要考查思维过程、创新能力和分析问题、解决问题的能力.命题者合理设置试题结构，减少机械性、记忆性试题比例，提高探究性、开放性、综合性试题比例，积极探索跨学科命题，提升试题情境设计水平，培养学生实践精神和创新精神，形成和发展核心素养.

2.落实“双减”“双升”，促进考教衔接

2023年云南省初中学业水平考试数学试题严格依据新课标，深化基础性和综合性，聚焦学科核心素养，精选试题情境，加强关键能力的考查，促进学生提升科学素养，引导全面发展，助推初中阶段育人方式改革.试题充分发挥基础学科的作用，在高度注重基础知识考查的同时，突出素养和能力的考查，通过双压轴题的设置来甄别思维品质、展現思维过程.命题者在解决问题方面，通过设置合适的运算过程和运算量，力求使情境化试题达到试题要求层次与学生认知水平的契合与贴切，给学生搭建展示的舞台和发挥的空间，致力于服务人才自主培养质量的提升和现代化建设人才的选拔;在反套路、反机械刷题方面下大功夫，突出强调对基础知识和基本概念的深入理解和灵活掌握，注重考查学科知识的综合应用能力，落实云南省“双减”“双升”政策的要求;在合理控制试题难度方面，科学引导初中教学，力图促进其与义务教育小学阶段和高中学段的有效衔接，促进考教衔接，引导学生提高在校学习效率，避免机械、无效的学习.

3.体现减负精神，回归核心本质

例1（2023年·17）計算：|-1|+（-2）2-（π-1）0+（）-1-tan45°.

【趋势解读】此类题型主要考查学生的计算能力，可能会以实数的运算、解不等式、解方程（组）、分式化简求值等形式出现.2023年和2021年的云南省初中学业水平考试数学试题都是以实数的运算来考查学生的运算素养，一般涉及加、减、乘、乘方运算，融入零指数幂、负整数指数幂、特殊角的三角函数值、去绝对值等知识点.2022年云南省初中学业水平考试数学试题解答题的第一题是统计题，解答题中没有考查实数运算，但依据课标的要求，加强数学运算能力素养的落实.此类题型是最基础、最核心的，学生好掌握、易得分，也必然是未来命题趋势上考查运算能力的重点题型之一，既落实“双减”要求，又回归教学本真.

【备考建议】实数的相关运算法则是基础且重要的知识点.教师必须引导学生熟练掌握，对于易错的知识点要注意辨别，并结合教学情况进行有针对性的训练;在解答过程中要引导学生规范书写，字迹清晰工整，确保在此类题目拿到满分.

例2 （2023年·18）如图1，C是BD的中点，AB=ED，AC=EC.求证：△ABC≌△EDC.

图1

【趋势解读】2023年和2021年的学业水平考试数学试题解答题的第二个题都是考查全等三角形的判定和性质的，一般情况只设置一问，是常考题型，属于简单题.本题主要是考查学生的逻辑推理能力.2022年云南省初中学业水平考试数学试题解答题的第二个题是概率题，解答题中没有考查全等三角形的证明，但依据课标的要求，落实好数学推理能力素养.此类题型也是最基础、最核心的，学生好掌握易得分，必然是未来命题趋势上考查简单逻辑推理能力的重点题型之一，既落实“双减”要求，又回归教学本真.

【备考建议】解答此类题型，需要学生熟练掌握证明三角形全等的五个判定定理，即SAS，ASA，AAS，SSS，直角三角形全等还有HL.在解答的过程中教师要注意引导学生加强逻辑推理的严谨性和书写的规范性，并用符号写出证明三角形全等所用的判定定理，不在解答过程中失分.

3.从“育分”到“育人”，培育核心素养

从2023年云南省初中学业水平考试数学试题来看，首先，试题严格依据课标命题，变“以考定教”为“以学定考”“以学定教”.其次，试题增强考查内容的基础性与情境性，既要考查学生的学科基础知识.如第4、7、9、11、16、19、20、21题等不仅考查学生数与代数、图形与几何、统计与概率、综合与实践四个领域的核心知识，还考查学生面对真实问题情境时表现出的情感态度、价值观念.又如，第1、2、4、6、7、11、16、19、20、21、24题等渗透传承传统文化、生活情趣和爱国情怀的情感价值.再次，试题创新命题形式，基于基本性、通用性及情境的典型性，着眼于社会发展与日常生活的应用性，最终服务于学生的创新发展.如第23、24题不仅着眼于学生图形模型应用能力、函数建模能力，更要求学生在解决问题中增强服务社会的意识.2023年云南省初中学业水平考试数学试题对初中数学教学具有指挥棒效应，对提高教学质量起到了积极的引导、促进作用，具有以评促教、以评促学和以评育人的功能，立足于学生的全面发展，“双减”政策下的学业水平考试向前迈出了一大步.

未来，结合新课标、新课程、新教材的落地实施，试题会更关注数学知识的应用，发挥数学应用广泛、联系实际的学科特点，同时选择具有时代气息和云南本土特色的素材创设情境，命制具有教育意义的试题，增强学生的社会责任感，引导学生学以致用，提升数学核心素养，重视运用数学必备知识、思想方法及数学模型解决实际问题，充分发挥核心素养的育人功能，促进学生全面发展、健康成长.

5.注重能力素养，难度区分有效

例3 （2023年·23）如图2，BC是☉O的直径，A是☉O上异于B、C的点.☉O外的点E在射线CB上，直线EA与CD垂直，垂足为D，且DA·AC=DC·AB.设△ABE的面积为S1，△ACD的面积为S2.

（1）判断直线EA与☉O的位置关系，并证明你的结论;

（2）若BC=BE，S2=mS1，求常数m的值.

图2

【趋势解读】2023年的第23题（倒数第二题）与2022年的第22题（倒数第二题）一样，都以圆为背景，设置两个小问，第（1）问主要是考查切线的证明，第（2）问涉及的知识多，综合程度高，入口较难，重在考查学生的逻辑推理能力，具有极大的挑战性，属于学业水平考试压轴题，承担选拔和区分的功能.

例4 （2023年·24）数和形是数学研究客观物体的两个方面，数（代数）侧重研究物体数量方面，具有精确性，形（几何）侧重研究物体形的方面，具有直观性.数和形相互联系，可用数来反映空间形式，也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题，充分利用代数、几何各自的优势，数形互化，共同解决问题.

同学们，请你结合所学的数学解决下列问题.

在平面直角坐标系中，若点的横坐标、纵坐标都为整数，则称这样的点为整点.设函数y=（4a+2）x2+（9-6a）x-4a+4（实数a为常数）的图象为图象T.

（1）求证：无论a取什么实数，图象T与x轴总有公共点;

（2）是否存在整数a，使图象T与x轴的公共点中有整点？若存在，求所有整数a的值;若不存在，请说明理由.

【趋势解读】2023年的第24题（最后一题）与2022年第23题（最后一题）一样，都是以二次函数为背景的代数推理问题.本题第（1）问考查了二次函数与一元二次方程的联系，需要用一次函数和二次函数分别证明函数图象T与x轴总有交点.抛物线与x轴交点的情况实际上就是对应的一元二次方程根的情况.从“形”的角度提出问题，用“数”的方法来解决问题相对简单一些，也就是用一元二次方程根的判别式来进行解答，该知识点往年一般以选择题的形式出现.本题第（2）问是在上一问的基础上进行升华的，考查分式整数解的问题，要求学生具备较高的数学素养方能解决.

2022年和2023年云南省学业水平考试数学压轴题放在最后两个大题中的最后一问，承担选拔、区分和控制满分率的功能，以能力立意，考查学生的数学核心素养的落实情况，既尊重了学生的数学水平差异，又能较好地区分不同数学水平的学生，较好地保证了区分结果的稳定性，从而确保试题具有良好的区分度.

【备考建议】在平时的教学过程中，教师除了要引导学生掌握好基础知识以外，还要有针对性地钻研拔高题，注重对模型的识别和归类，总结相应的解题技巧和解题方法，精讲精练，旨在提升学生的代数推理能力和几何推理能力.代数推理往往以二次函数为背景，结合数、方程或不等式来进行推理.几何推理可能以圆为背景或者以特殊四边形为背景进行考查，要有意识地调整学习策略，针对命题趋势进行训练，精准备考.

三、新课标理念下的备考建议

1.基于课程标准，立足课堂教学

2023年云南省学业水平考试数学试题结合新课标，依标命题，教考衔接，引导教学重视课堂、重视教材，鼓励教师挖掘教材中的素材，促进学生在课堂上積极探索、主动学习，重视知识的形成过程.在课堂教学中，一方面，教师要以教材内容为教学载体，设计和选择能够引发学生思考的教学方式，注重启发式、探究式、参与式、互动式等教学方式;另一方面，要强化情境的设计和问题的提出，注重发挥情境设计和问题提出对学生主动参与教学活动的促进作用，围绕教学任务，选择贴近学生生活经验、适合学生年龄特点和认知层次的素材，以体现数学学科的育人功能.

2.内容形成结构，整体设计教学

新课标中明确提出，教师要整体把握教学内容，注重教学内容的结构化，注重教学内容与核心素养的关联，重视单元整体教学设计.例如，在“数与代数”领域中，运算能力应该是贯穿学习始终的，教师可以尝试从明确运算对象、理解运算法则、求得运算结果、优化运算过程的角度，形成基于发展学生运算素养的单元教学设计;改变过于注重以课时为单位的教学设计，合理整合教学内容，分析主题-单元-课时的数学知识和核心素养的主要表现，确定单元教学目标，并落实到教学活动的各个环节中.

3.注重归纳反思，加强错题管理

注重归纳反思各部分内容的基本问题，建立错题集，分门别类、管理错题、分析错因、纠正错误.错题通常是如下几种情况：一是会做但做错的，原因可能是审题不清、误写和表达不规范等;二是来不及做的，原因包含题量过大或者解题效率低下;三是能力不够，确实不会做的.教师应引导学生针对不同错因采取有效措施，争取在考试中尽量做对.错题管理重在日积月累，落实到位，养成习惯.

4.积极应对调整，高效复习备考

掌握指导看要求，钻研教材找标准，研究考题看形势，推敲评价找方向.2024年云南省初中数学学业水平考试的时间为120分钟，满分为100分，但试题的分值结构发生变化，客观题（选择题和填空题）共38分，主观题（解答题）共62分.第一部分为选择题，15个小题，每小题2分，共30分，设置难度均为易.第二部分为填空题，4个小题，每小题2分，共8分，设置难度均为易.第三部分为解答题，共8个小题，共62分，其中第20、21、22、23题分值分别为7分、6分、7分、6分，设置难度均为易;第24、25题分值均为8分，设置难度均为中等;第26题8分，设置难度为3分易、5分难;第27题12分，设置难度为3分易、4分中等、5分难，整套试卷难易度（易、中、难）比例保持为7∶2∶1.面对变化，广大教师要积极调整教学策略，落实“四基”、培养“四能”、发展“三会”，通过“讲知识，讲思想，讲方法，讲策略”来达到“求效率，求质量，求提高，求创新”的目标，注重知识的“生长点”与“延伸点”，落实核心素养，注重学科课程思政，体现数学学科的育人价值，全面落实“双减”政策，在取得好成绩的同时切实减轻学生过重的课业负担.

◇责任编辑 邱 艳◇