运营高铁箱梁顶升平移纠偏关键控制参数及结构稳定性分析

朱江江,俞 添,陈 占

(中铁第四勘察设计院集团有限公司,武汉 430063)

引言

在长期运营过程中，高速铁路受线路周边堆卸载、抽水、工程建设等多种因素影响，部分高铁桥梁地段出现了超出扣件系统可调范围的横向偏移，严重影响了列车正常安全运行。因此，开展无砟轨道桥梁横向偏移病害整治相关研究，使高速铁路长期保持安全、平稳、舒适运行具有重要意义[1-2]。

目前，国内外学者针对桥梁地段出现的横向偏移问题进行了诸多研究。在成因机理方面，王崇淦[3]、董亮[4]、梁育玮[5]等分析大面积单侧堆载对高铁桥梁墩台的影响，揭示了单侧堆载是无砟轨道桥梁地段出现横向偏移的重要原因；胡军[6]、王菲[7]、潘振华[8]等通过数值分析以及现场位移、水位等实时检测手段，计算了基坑开挖及抽水对高速铁路桥梁桩基变形的影响规律及范围；王景春等[9]以某立交匝道桥下穿高速铁路桥梁为背景，研究了桩基施工与运营阶段对高铁群桩基础变形的影响。姜惠峰[10]依托京津城际无砟轨道桥梁沉降修复工程，通过理论与实践相结合的方式，验证了桥梁沉降顶升修复的可行性。袁新华等[11]依据摩擦阻荷原理设计了一套竖向和横向顶推联动装置，在北郊河桥的纠偏施工中得到了成功应用。陈占等[12-13]在大量文献调研及工程实践基础上，提出一种用于运营高速铁路桥梁无砟轨道结构纠偏的方法，形成了相关专利，已应用于10余条线路100多片箱梁的纠偏施工。孙明德等[14]以一座在建铁路连续梁桥桥墩的球型支座，提出了单墩顶升梁体更换支座的整治方案，并采用数值模拟分析了不同顶升高度时的梁体应力。刘竞等[15]通过建立无砟轨道结构力学模型，分析了顶推纠偏对无砟轨道各结构层受力与变形的影响。马慧君等[16]针对无砟轨道桥梁墩身差异沉降，通过实时监测抬梁过程中轨道结构的应力和位移变化情况，评估了无砟轨道和桥梁结构的安全性能。

综上所述，采用顶升平移的方式进行桥梁地段线路纠偏是一项有效技术措施，并在大量工程实践中得到了成功应用，但已有研究大多以施工工艺为主，相应的关键控制参数研究则较少[17-19]。因此，本文通过建立数值模型，分析不同顶升高度及平移量下轨道结构的应力变化规律，探讨纠偏施工中的关键控制参数；同时选取最不利工况，对不同偏移量下轨道结构的稳定性进行检算，以期为运营高铁箱梁顶升平移纠偏现场施工提供技术指导。

1 顶升平移纠偏技术

无砟轨道桥梁纠偏是采用桥墩自身作为顶升平移纠偏反力系统，通过在梁底和墩顶位置布设联动装置，利用竖向千斤顶摩擦力平衡水平千斤顶顶推反力，在不单独设置反力装置的情况下，对箱梁进行顶升平移，调整梁体位置，恢复线路线形的新型纠偏技术，其工作原理如图1所示。

图1 箱梁顶升平移纠偏工作原理

顶升平移纠偏联动装置主要由2组千斤顶组成，每组千斤顶包括多个竖向千斤顶和1个水平千斤顶，竖向千斤顶用于箱梁顶升，水平千斤顶用于箱梁平移。每个竖向千斤顶包含1个伪固定面和1个滑动面，通过竖向千斤顶摩擦力平衡水平千斤顶顶推反力，实现对箱梁的横向平移。该技术不受轨道结构和场地条件限制，无需单独布设反力装置，具有适用性强、施工效率高等技术特点，通过采用PLC多点同步液压控制系统进行施工，纠偏精度可控制在2 mm以内，在简支梁地段已取得成功应用。

2 顶升平移纠偏数值模拟

2.1 数值模型建立

现依托某高铁桥梁偏移整治工程，选取其中4跨简支梁及CRTSⅢ型板式无砟轨道结构，建立轨-梁-墩实体模型，模型从上至下依次为：钢轨、轨道板、砂浆层、底座板、箱梁(包括预应力钢绞线)、支座、桥墩，模型横断面如图2所示[20]。

图2 轨-梁-墩实体模型横断面

模型中轨道和桥梁结构为Hex单元，采用C3D8R单元类型；预应力钢绞线为Truss单元，采用T3D2单元类型，不设置普通钢筋；模型网格划分如图3所示。

图3 网格划分完成后的轨-梁-墩实体模型

2.2 计算参数选取

模型中箱梁尺寸参照《预制无砟轨道后张法预应力混凝土简支箱梁(双线)》(图号：通桥(2016)2322A-II-1)铁路工程建设通用参考图，长度为32.6 m，梁缝宽0.1 m，底座板与箱梁等长；每片箱梁上布设4块5.6 m和2块4.925 m长的轨道板，板间缝隙0.07 m，砂浆层与轨道板布设方式一致；钢轨为60 kg/m标准轨，总长130.7 m；扣件垂向、横向、纵向刚度分别为35，50，15 MN/m；每跨简支梁左侧桥墩为固定支座，右侧桥墩为活动支座，支座尺寸按《铁路桥梁球型支座(TJQZ)安装图》(图号：TJQZ-8360)取值，桥墩为双柱墩形式；轨道结构双线布设，模型部件尺寸及材料属性如表1所示。

表1 模型部件尺寸及材料属性

2.3 荷载及边界条件

由于顶升平移纠偏在“天窗点”期间施工，计算时不考虑列车荷载作用，仅有结构自重与二期恒载，顶升和平移施工工况通过施加位移实现。模型中钢轨与轨道板之间的扣件采用弹簧阻尼单元模拟，扣件间距0.63 m，其余各部件之间采用绑定约束；固定支座在X、Y和Z方向固定，纵向活动支座在X和Y方向固定、Z方向自由，桥墩底面完全固定U=R=0，线路两端在X、Y和Z方向固定。

2.4 施工工况模拟

为分析顶升和平移对轨道结构的影响，共设置24种不同工况，顶升和平移施工分为单点和隔墩2种方式，顶升高度和平移量大小共6种，数值模拟工况如表2所示。

表2 顶升和平移施工数值模拟工况

3 顶升平移纠偏关键控制参数

箱梁顶升高度和平移量是顶升平移纠偏施工的关键控制参数，其大小直接影响轨道结构受力状态，现对不同工况下的轨道结构应力进行分析，确定施工过程中的单次最大顶升及平移量。

3.1 竖向顶升对轨道结构影响分析

竖向顶升计算工况分为单点顶升和隔墩顶升，顶升高度分别为0，5，10，15，20 mm和30 mm，现以顶升10 mm工况为例，分析对轨道结构的影响，计算的各结构层应力云图如图4所示。

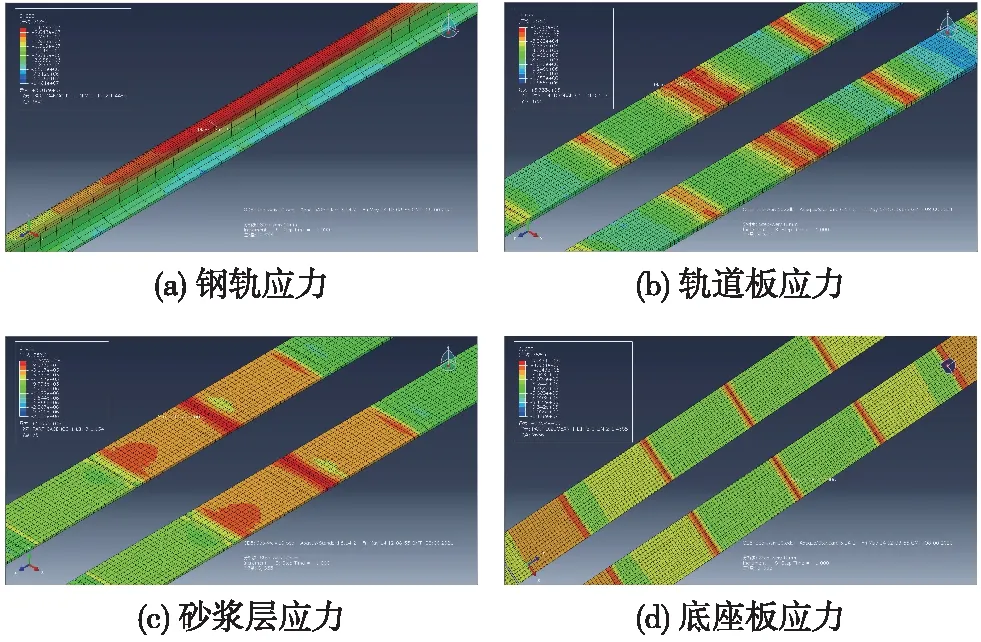
图4 单点顶升10 mm工况各结构层应力云图(单位：Pa)

根据计算结果，钢轨最大应力出现在顶升点上方，钢轨顶面最大拉应力为30.12 MPa；轨道板最大应力出现在相邻桥墩上方梁缝处，最大拉压应力分别为0.57 MPa和1.86 MPa；砂浆层最大应力出现部位与轨道板一致，最大拉压应力分别为0.13 MPa和2.53 MPa；底座板最大应力出现在顶升点两侧的梁跨中部，最大拉压应力分别为1.63 MPa和9.34 MPa。各轨道结构层应力均小于C40混凝土抗拉压强度标准值2.39 MPa和26.8 MPa，并以抗拉强度为控制指标，因此后续分析中仅考虑拉应力的影响。

隔墩顶升10 mm工况下，钢轨、轨道板、砂浆层和底座板的最大拉应力分别为32.87，0.59，0.14 MPa和1.64 MPa，与单点顶升工况下相差不大，并均小于相应材料的强度值。

3.2 横向平移对轨道结构影响分析

横向平移计算工况分为单点平移和隔墩平移，两种平移方式均在顶升高度为10 mm条件下进行，平移量分别为0，5，10，15，20和30 mm，现以平移10 mm工况为例，分析对轨道结构的影响，计算的各结构层应力云图如图5所示。

图5 单点平移10 mm工况各结构层应力云图(单位：Pa)

根据计算结果，钢轨最大应力出现在平移点上方，钢轨顶部侧面最大拉应力为54.32 MPa；轨道板最大拉应力出现在相邻桥墩上方梁缝处，最大值为0.74 MPa；砂浆层最大拉应力出现部位与轨道板一致，最大值为0.20 MPa；底座板最大拉应力出现在平移点两侧的梁跨中部，最大值为1.78 MPa；各轨道结构层应力均小于C40混凝土抗拉强度标准值。

隔墩平移10 mm工况下，钢轨、轨道板、砂浆层和底座板的最大拉应力分别为58.35，1.12，0.75 MPa和1.80 MPa，与单点平移工况下相差不大，并均小于相应材料的强度值。

3.3 现场实测数据对比分析

为检验数值模拟的计算结果，在某高铁秦淮河3号特大桥桥梁偏移整治工程中，对轨道结构的应力状态进行了现场监测，根据实测数据绘制的轨道板和底座板的应力变化规律如图6所示。

图6 轨道板和底座板实测应力变化规律

由图6可知，顶升平移纠偏对轨道结构的影响不大，施工引起的轨道板和底座板应力变化范围分别为-0.23～0.79 MPa和-1.15～0.57 MPa。在单点平移工况下，采用数值模型计算的轨道板和底座板应力分别为0.74 MPa和1.78 MPa。通过对比分析，计算值与实测值基本接近，表明所建数值模型及计算结果较为可靠。

3.4 单次最大顶升及平移量确定

根据不同顶升工况下的计算结果，各轨道结构层拉应力与顶升高度之间的关系曲线如图7所示。

图7 不同顶升工况下各结构层拉应力

由图7可知，在不同顶升工况下，随着顶升高度增加，钢轨和轨道结构拉应力逐渐增大，并且隔墩顶升工况下的应力略大于单点顶升工况。当顶升高度在30 mm以内时，钢轨和轨道结构拉应力均未超过强度标准值；但顶升高度大于10 mm后，各结构层拉应力显著增大。同时现场实际施工表明，顶升高度达到5～8 mm时，既有支座与支撑垫石已能较好分离，可满足横向平移要求。因此，为尽量减小施工对轨道结构的影响，建议最大顶升高度为10 mm，极值控制在30 mm以内。

在顶升10 mm状态下，根据不同平移工况下的计算结果，各轨道结构层拉应力与平移量之间的关系曲线如图8所示。

图8 不同平移工况下各结构层拉应力

由图8可知，在不同平移工况下，随着平移量增加，钢轨和轨道结构拉应力逐渐增大，并且隔墩平移工况下的应力略大于单点平移工况。以隔墩平移工况下轨道板拉应力作为控制条件，最大平移量不应超过20 mm。考虑平移量大于10 mm后各结构层拉应力显著增大，同时为尽量减小施工对轨道结构的影响，建议采用多次少量的方式进行箱梁平移，单次最大平移量为10 mm，单个“天窗点”累计平移量控制在20 mm以内，并加强对轨道结构应力状态的监测。

4 顶升平移纠偏结构稳定性分析

根据顶升平移纠偏施工工艺，施工过程中桥梁结构历经几种不同受力状态，通过对比整个施工过程，选取最不利工况分析桥梁结构稳定性。

4.1 桥梁结构受力最不利工况

顶升平移纠偏过程中，在箱梁横向平移完成、既有支座灌浆定位前，上部荷载全由临时支座承担时(临时支座间距2.5 m)，桥梁结构处于最不利状态。根据我国高速铁路机车车辆主要技术参数，动车组车辆全长在25 m时，车辆定距和固定轴距可分别取17.5 m和2.5 m；由于箱梁长32.6 m，当一车厢位于箱梁中部，前车厢的后转向架与后车厢的前转向架均位于此箱梁上时，为最不利工况。为分析顶升平移纠偏过程中桥梁结构稳定性，分别计算了正常条件、临时支座支撑状态以及箱梁偏移10，30，50，80，120 mm和200 mm共计8种工况下，箱梁和桥墩应力以及支座反力的变化规律。

4.2 数值模型荷载施加

根据TB 10002—2017《铁路桥涵设计规范》，计算时荷载应考虑主力与一个方向(顺桥或横桥方向)的附加力相结合。主力主要包括列车竖向动力作用、离心力和横向摇摆力；附加力为顺桥向制动力。列车竖向动力作用可按竖向静活载乘以动力系数确定，根据文献[21]中ZK和ZC活载，计算的高速铁路和城际铁路桥梁结构动力系数为1.08，列车轴重取17 t，则列车竖向动力作用为183.6 kN。曲线上桥梁应考虑列车竖向静活载产生的离心力，当曲线半径取7 000 m时，列车离心力为44.2 kN，水平向外作用于钢轨顶面以上1.8 m处。高速铁路横向摇摆力为80 kN，多线桥梁可仅计算任一线，横向摇摆力作为一个集中荷载取最不利位置，以水平方向垂直线路中线作用于钢轨顶面。列车制动力按计算长度内列车竖向静活载的10%计算，双线桥梁按任一线考虑；根据ZK标准活载图式计算的制动力为173.4 kN，作用于钢轨顶面以上2 m处。

4.3 箱梁和桥墩应力状态分析

最不利工况下轨道结构受力状态变化不大，因此只检算临时支座支撑运行情况下，箱梁和墩身的应力。现以偏移量80 mm工况为例，分析桥梁结构受力状态，箱梁的应力云图(S22)如图9所示。

图9 最不利工况下箱梁应力云图(偏移80 mm)(单位：Pa)

由图9可知，在临时支座支撑状态下，当偏移量为80 mm时，箱梁最大应力出现在与临时支座的接触部位，不考虑因支座刚度较大导致的应力集中现象，箱梁的最大拉应力为1.64 MPa，略小于C50混凝土的抗拉强度设计值1.89 MPa，抗拉强度满足规范设计要求。计算得到的墩身应力云图(S22)如图10所示。

图10 两种工况下墩身应力云图(单位：Pa)

由图10可知，在正常条件下，桥墩顶部最大应力位于既有支座垫石附近，墩身应力呈对称分布；临时支座支撑状态下，桥墩顶部最大应力位于临时支座垫石附近，且墩身应力向一侧转移。正常条件下桥墩主要承受竖向压应力，仅在桥墩底端出现微小拉应力，最大拉压应力分别为0.17 MPa和8.95 MPa；临时支座支撑状态下，偏移量为80 mm时，最大拉压应力则增加至1.80 MPa和15.57 MPa；但仍小于C35混凝土抗拉压强度标准值2.2 MPa和23.4 MPa。

根据不同工况下的计算结果，箱梁和墩身应力与偏移量之间的关系曲线如图11所示。

图11 不同工况下箱梁和墩身应力变化规律

由图11可知，箱梁和墩身应力随支座支撑状态和偏移量的增大逐渐增加，当偏移量达到80 mm后，箱梁拉应力发生显著变化，已超过C50混凝土抗拉强度2.64 MPa。但即使偏移量增大至200 mm，墩身拉压应力1.80 MPa和19.13 MPa，也未超过C35混凝土抗拉压强度2.2 MPa和23.4 MPa。因此，顶升平移纠偏过程中箱梁的拉应力为控制条件，在列车不降速运行情况下，可实施的最大纠偏量为80 mm，此时墩身不开裂，但应重点监测箱梁底部拉应力。

4.4 轨道结构稳定性分析

根据不同工况下支座的受力状态，绘制支座反力与偏移量之间的关系曲线如图12所示。

图12 不同工况下支座反力变化规律

由图12所示，在上部结构和列车荷载作用下，随支座支撑状态和偏移量的增大，位于同侧的1号和3号支座反力逐渐增大，相应的另一侧2号和4号支座反力逐渐减小，但支座反力总和均在14 910 kN附近。当偏移量达到80 mm后，1号和3号支座反力发生显著变化，已超过铁路桥梁常用TGPZ-5000-0.10g型盆式橡胶支座的承载能力，甚至会有被倾覆风险。因此，为保证轨道结构稳定性，顶升移梁纠偏时的最大平移量应控制在80 mm以内。

5 结论

针对部分高铁桥梁地段出现的横向偏移问题，本文通过建立轨-梁-墩实体数值模型，探讨了纠偏施工中的关键控制参数，同时选取最不利工况，检算了不同偏移量下桥梁结构的稳定性，得到了以下结论。

(1)单点平移10 mm工况下，数值计算的轨道板和底座板应力分别为0.74 MPa和1.78 MPa，现场施工实测的应力变化范围分别为-0.23～0.79 MPa和-1.15～0.57 MPa，计算值与实测值基本接近，所建数值模型及计算结果较为可靠。

(2)随着顶升高度和平移量增加，轨道结构应力逐渐增大，为尽量减小纠偏施工对轨道结构的影响，建议最大顶升高度为10 mm，极值控制在30 mm以内，单次最大平移量为10 mm，单个“天窗点”累计平移量控制在20 mm以内。

(3)箱梁和墩身应力以及支座反力随支撑状态和偏移量的增大逐渐增加，以箱梁拉应力和支座反力作为控制条件，为保证轨道结构的稳定性，在高铁列车不降速运行情况下，可实施的最大纠偏量为80 mm，同时应重点监测箱梁底部拉应力。