重载铁路典型波磨区段轮轨力仿真分析

肖炳环,牛留斌,刘金朝,张 昭,周素霞

(1.中国铁道科学研究院研究生部,北京 100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所,北京 100081；3.北京建筑大学机电与车辆工程学院,北京 100044)

引言

重载铁路因其运能大、效率高、运输成本低而受到世界各国铁路的广泛关注。重载运输已被国际公认为铁路货运发展的方向，成为世界铁路发展的重要趋势[1-2]。随着重载铁路的发展，其轴重越来越大，线路设备所承受的荷载较大，尤其钢轨更是病害发生的集中部位。常见的一种病害就是钢轨波磨，钢轨波磨是指沿钢轨纵向出现的波浪形不均匀磨损[3]。车辆经过钢轨波磨区段时，会产生较大振动，引起异常的轮轨力，造成车辆、轨道、扣件等各结构部件产生疲劳损伤，严重时会危及列车行车安全。

轮轨关系一直是铁路行业重点关注对象，国内外众学者建立了很多仿真模型进行探究。1996年，IGELAND[4]基于接触力学关系，研究了在非线性赫兹轮轨刚度接触条件下车轮与钢轨间的接触力情况。2009年，OYARZABAL O[5]等研究了14个轨道参数对波磨的影响，发现轨枕间距、轨枕质量、垫块垂直刚度、垫块横向刚度和道碴垂直刚度这5种参数影响更大。2016年MEEHAN P A[6]等建立了轮轨耦合动力学模型，研究了车辆在弯道运行时车辆运行速度对钢轨波磨生长的影响，研究结果表明，控制车辆在弯道的倾斜程度可以降低波磨的生长速率。2019年AMIN K[7]等建立了二维数值模型，考虑了短波产生的高频激励效应，研究了在具有谐波不平顺的平板轨道中轨垫刚度对轮轨力的影响。研究结果表明，在低频范围内，轮轨力随着轨垫刚度的增加而增加。

2015年，丁荣[8]等建立重载铁路轨道结构仿真模型，分析了不同轴重及不同轨道参数下的轨道结构受力特性，发现列车轴重对钢轨位移与应力影响最大。2018年，吴斌[9]等通过分析获得30 t轴重列车的大量轮轨力实测数据，揭示不同轴重重载列车作用下轮轨垂向力分布特征以及变化规律。2020年，周成[10]等为分析高速铁路钢轨波磨对轮轨力的影响，建立三维轮轨瞬态动力学模型，发现波磨会导致轮轨垂向力、轴箱和钢轨垂向振动加速度等指标出现高频振动特征。2020年WANG[11-13]等利用ABAQUS建立了轨道三维有限元模型，研究了地铁轨道的固有频率和产生波磨频率之间的关系，基于轮轨接触耦合动力学模型，研究了轨道切向断面波磨的原因和生长特点，并且分析了轨道结构参数和车辆运行速度对钢轨波磨产生和生长的影响。2021年MA[14]等建立了柔性双车轮轨耦合动力学模型，根据钢轨波磨生长速率揭示了钢轨波磨的起裂机理。CUI[15]等建立了钢轨波磨有限元模型，研究了轮轨间的摩擦振动对诱发钢轨波磨的影响。

波磨产生机理及其影响因素研究取得了大量的成果，但是重载铁路钢轨波磨波长对轮轨力的影响至今还没有达成共识。为分析重载铁路典型波长下的轮轨力，本文结合铁路现场钢轨波磨情况，利用有限元仿真分析技术，通过控制变量法，计算不同波长的钢轨波磨区段轴重、速度、扣件刚度、阻尼等参数对轮轨力的影响，探究不同波长参数下波磨区段轮轨力影响因素，为重载线路波磨区段的养护维修提供理论指导。

1 重载波磨动态响应特性分析

中国幅员辽阔、资源丰富、煤炭等货物运量占有率高，重载铁路能带来更便捷的服务。因此重载铁路的发展从1984年开始建设以来，一直在走“速度快、密度高、质量大”的道路。至今已建成年运量超亿的大秦铁路、神朔铁路、侯月线和朔黄铁路。

在发展的同时也要检测和监测铁路状态，进行预防性维修和保证车辆-线路系统处于良好运营状态[16]。钢轨波磨作为常见的重载铁路病害之一，要及时打磨防止其继续恶化带来的不利影响。然而，波磨波长一般较短，无法从轨道几何检测识别这类短波病害，因此利用轴箱加速度检测短波病害成为近几年发展趋势[17-19]。

分析某重载铁路线路轴箱加速度数据，发现其上行里程K140～K142、K272～K274、K385～K388等多个区段的轴箱加速度振幅较大，且通过功率谱分析发现此区段数据周期性较强，波长集中在200～300 mm，复核发现现场存在波磨且波磨波长约为280 mm。以K372+550～K372+600为例，轴箱加速度波形如图1(a)所示，计算功率谱结果如图1(b)所示，波磨波长为283 mm。现场复核时发现该区段存在钢轨波磨现象。

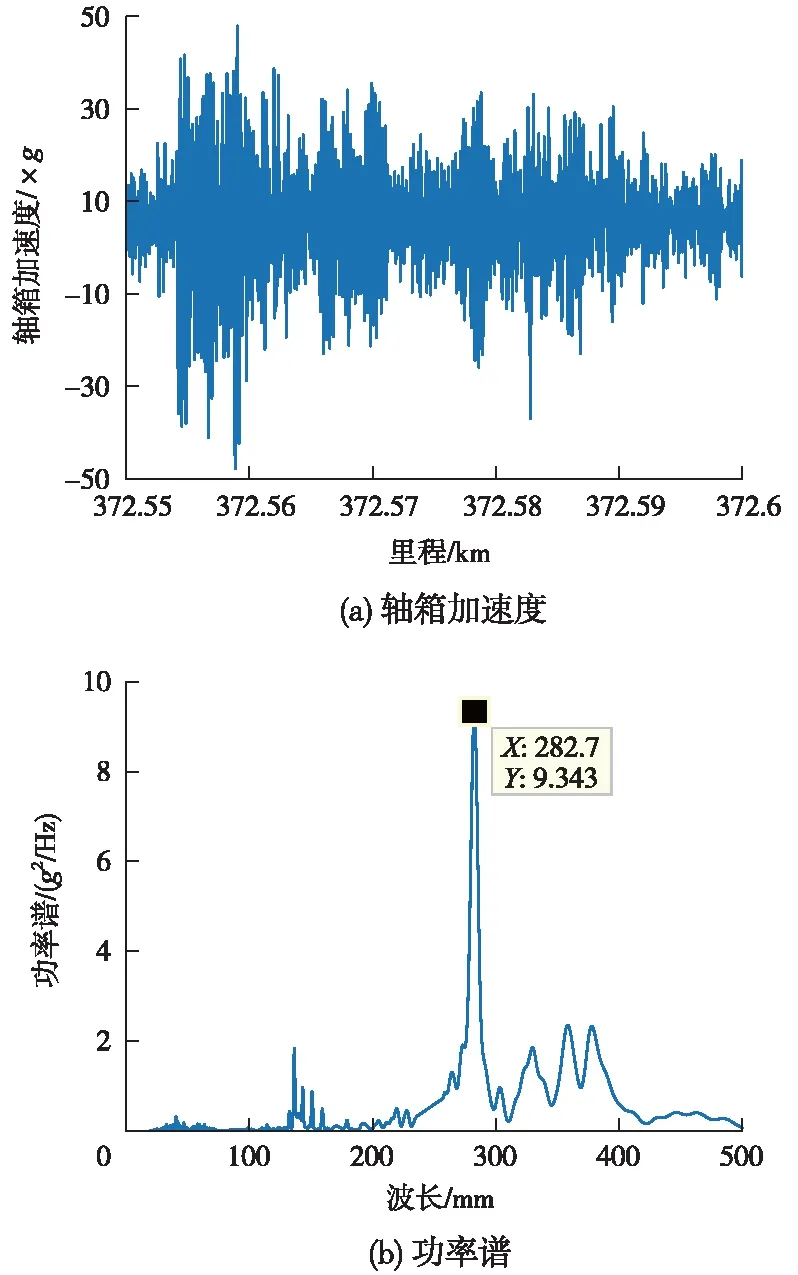
图1 K372+550～K372+600轴箱加速度和功率谱

利用波磨小车采集该区段轨面平直度数据，如图2(a)所示。同样计算其功率谱，如图2(b)所示。采样频率是500 m-1，该区段波磨对应波长为285 mm，与现场钢轨表面波磨波长相符，现场轨面情况如图3所示。

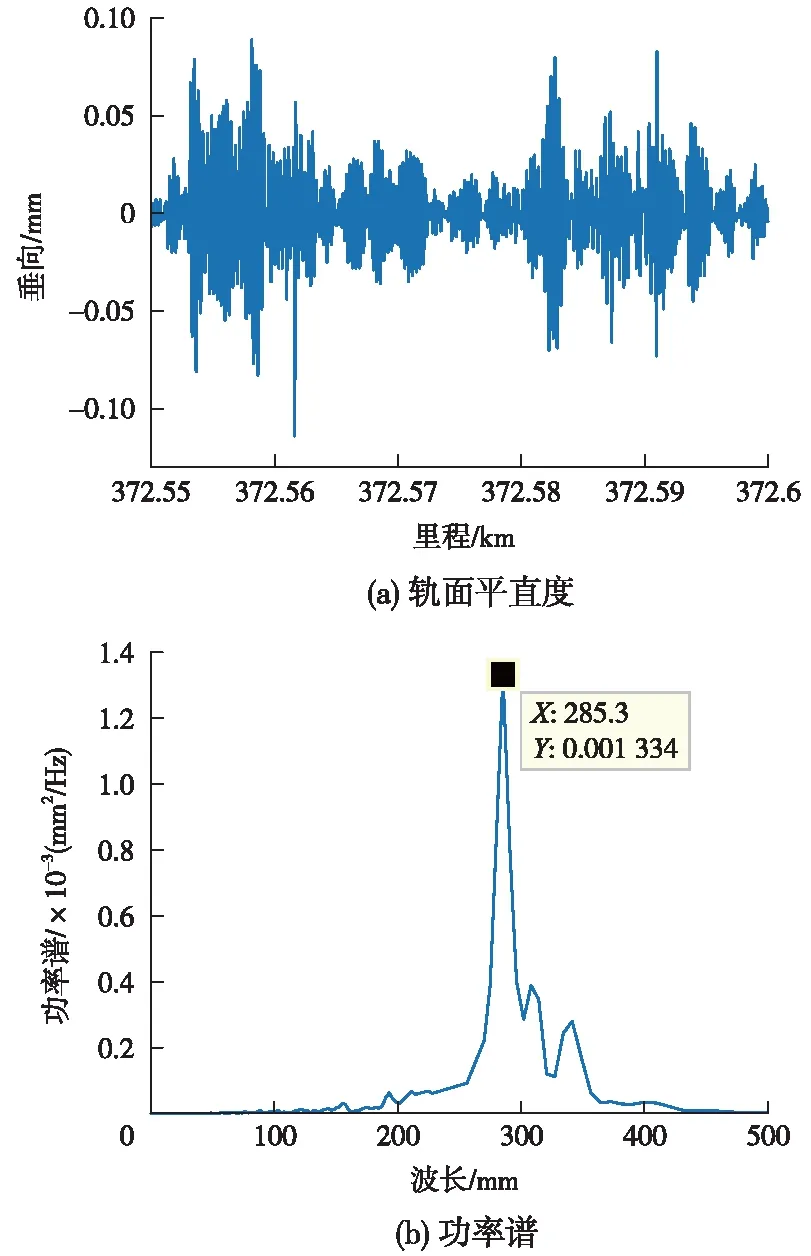
图2 K372+550～K372+600轨面平直度和功率谱

图3 重载铁路上行K372+590附近钢轨表面情况

分析其他区段轴箱加速度时疑似存在波长120 mm左右的波磨区段。经过现场复核，确认了该区段存在波磨，且波磨波长为120 mm，现场轨面情况如图4所示。可见，重载铁路也存在100 mm左右波长的波磨。为了与280 mm波长的波磨区段作对比，另一个模型波长设为120 mm。

图4 重载铁路120 mm钢轨波磨

2 重载波磨高频有限元建模

本研究中利用有限元分析软件ABAQUS进行模拟，建立的三维有限元模型如图5所示。考虑缩短计算规模，模型分为四部分，分别为车体、钢轨、车辆轮对以及道床，其中，车体用一个刚性单元代替，钢轨、轮对以及轨道板尺寸信息基于现场实际测量数据建立，并根据铁路现场典型波磨信息对模型中钢轨施加波磨，波磨波长分别设置为280 mm和120 mm，波深0.1 mm。

图5 轮轨接触三维有限元模型

为更好地还原真实情况，模型中钢轨与道床连接的扣件采用11组弹性元件模拟，每组弹性元件包含2个弹性单元，其垂向刚度为5 000 N/m，阻尼为7 N·s/mm，相邻弹性单元之间的距离为130 mm，每组弹性元件之间的距离为650 mm；采用横向弹簧和垂向弹簧模拟列车的一系悬挂，其中横向弹簧刚度为918 N/mm，垂向弹簧刚度为750 N/mm，弹簧阻尼系数为10 N·s/mm[20]。

按照我国重载线路及典型车辆参数建立轮轨有限元模型，采用旋转建模、过渡网格以及加密网格的方法离散轮对有限元模型，以六面体网格为主，考虑到钢轨与轮对的接触问题，对自钢轨的轨顶面向下10 mm距离的部位进行网格细化，网格细化为2 mm使之与轮对踏面部分的网格相同。其余远离轮轨接触部位如轨枕、路基等采用较大的网格尺寸。局部网格划分如图6所示。

图6 轮轨网格划分方式

根据现场车辆的实际运行情况，同时考虑模型收敛性，车轮与钢轨之间设置为罚函数，表面与表面接触。由于轮轨接触问题是一动态问题，故在有限元分析软件ABAQUS中对模型设置动力显示分析步，时间增量通过中心差分法求解[21]。

(1)

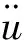
图7 轮轨接触边界条件示意

为验证模型的有效性，利用轨道检查车实测的轮轨接触力与有限元模型数值计算结果作对比。图8中实线是实测轨道不平顺条件下输入轨道模型得到的轮轨垂向力仿真波形，虚线是实测轮轨垂向力数据。从图8中可知，两波形吻合良好且趋势一致。计算其相关系数为0.82，说明两组数据之间存在较强的线性相关性。

图8 轮轨垂向力仿真结果与实测对比

3 关键参数影响特性分析

通过控制变量法，计算两种波磨波长情况下不同车辆轴重、列车速度、弹簧阻尼和扣件刚度参数的轮轨垂向力，然后进行对比分析。作为对照组，参数设置如下：轴重25 t，速度60 km/h，弹簧阻尼10 N·s/mm，扣件刚度5 000 N/m。120 mm和280 mm两种波长下轮轨垂向力如图9所示。

比较图9中两种波长下的轮轨垂向力，120 mm波长下轮轨力标准差为36.81 kN，280 mm波长下轮轨力标准差为29.05 kN。可以发现，120 mm波长对应的轮轨力波动范围比280 mm波长的大。接下来，分别改变车辆轴重、列车速度、弹簧阻尼和扣件刚度，对比两种波长下时的轮轨垂向力。

图9 重载铁路两种波磨区段轮轨垂向力对比

3.1 轴重影响

仅改变轴重参数，当车辆轴重15 t时，两种波长下的轮轨垂向力结果如图10所示，120 mm波长下轮轨力标准差为30.86 kN，280 mm波长下轮轨力标准差为21.89 kN；当车辆轴重30 t时，两种波长下的轮轨垂向力结果如图11所示，120 mm波长下轮轨力标准差为39.5 kN，280 mm波长下轮轨力标准差为33.66 kN。可以发现，当车辆轴重不同时，120 mm波长对应的轮轨力波动比280 mm波长的大。

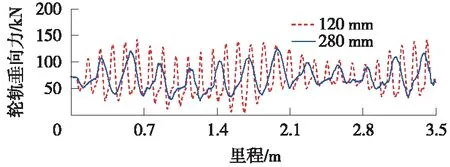
图10 15 t轴重两种波磨区段轮轨垂向力对比

图11 30 t轴重两种波磨区段轮轨垂向力对比

3.2 速度影响

仅改变速度参数，当列车辆速度30 km/h时，两种波长下的轮轨垂向力结果如图12所示，120 mm波长下轮轨力标准差为33.39 kN，280 mm波长下轮轨力标准差为23.95 kN；当列车车辆速度90 km/h时，两种波长下的轮轨垂向力结果如图13所示，120 mm波长下轮轨力标准差为44.69 kN，280 mm波长下轮轨力标准差为35.31 kN。可以发现，当列车速度不同时，120 mm波长对应的轮轨力波动比280 mm波长的大。

图12 30 km/h两种波磨区段轮轨垂向力对比

图13 90 km/h两种波磨区段轮轨垂向力对比

3.3 扣件刚度影响

仅改变扣件刚度参数，当刚度为3 500 N/m时，两种波长下的轮轨垂向力结果如图14所示，120 mm波长下轮轨力标准差为36.59 kN，280 mm波长下轮轨力标准差为28.74 kN；当刚度为6 500 N/m时，两种波长下的轮轨垂向力结果如图15所示，120 mm波长下轮轨力标准差为37.5 kN，280 mm波长下轮轨力标准差为29.17 kN。可以发现，当扣件刚度不同时，120 mm波长对应的轮轨力波动比280 mm波长的大。

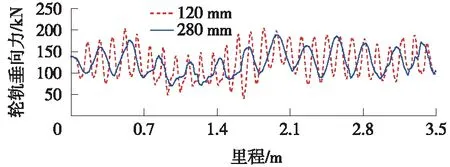
图14 3 500 N/m两种波磨区段轮轨垂向力对比

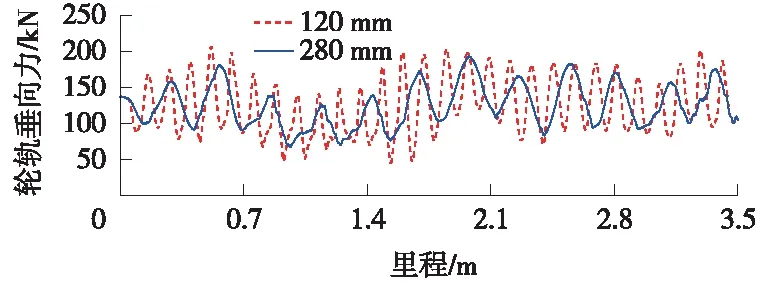
图15 6 500 N/m两种波磨区段轮轨垂向力对比

3.4 弹簧阻尼影响

仅改变弹簧阻尼参数，当阻尼为7 N·s/mm时，两种波长下的轮轨垂向力结果如图16所示，120 mm波长下轮轨力标准差为39.08 kN，280 mm波长下轮轨力标准差为24.53 kN；当阻尼为13 N·s/mm时，两种波长下的轮轨垂向力结果如图17所示，120 mm波长下轮轨力标准差为36.79 kN，280 mm波长下轮轨力标准差为33.54 kN。可以发现，当弹簧阻尼不同时，120 mm波长对应的轮轨力波动比280 mm波长的大。

图16 7 N·s/mm两种波磨区段轮轨垂向力对比

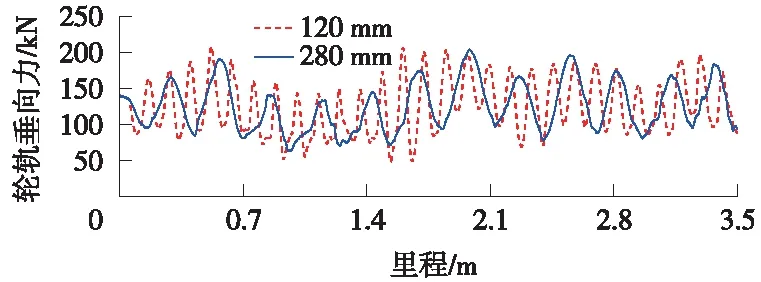
图17 13 N·s/mm两种波磨区段轮轨垂向力对比

本节通过对比不同参数下的轮轨垂向力仿真结果发现，相同工况下，120 mm波长对应的轮轨垂向力波动都比280 mm波长的大。

4 结论

针对重载铁路不同波长的钢轨波磨区段轮轨垂向力问题，建立重载铁路高频有限元模型，结合铁路现场实测数据，使用控制变量法计算了不同波长波磨区段的轮轨垂向力。通过对比不同车辆轴重、运行速度、扣件刚度和弹簧阻尼，不同波磨波长下的轮轨垂向力，发现在相同工况下，相比于波长较大的波磨区段，短波长造成的轮轨垂向力波动性更大。因此，在重载铁路养护维修时应及时打磨钢轨波磨，防止因异常的轮轨力造成轨道恶化，造成部件伤损和安全问题。研究成果为铁路工务提供理论指导，以保持良好的轨道健康状态。