全附体潜艇的PMM仿真实验❋
张大朋,严 谨,赵博文,朱克强
(1.广东海洋大学船舶与海运学院,广东 湛江 524088;2.浙江大学海洋学院,浙江 舟山 316021; 3.宁波大学海运学院,浙江 宁波 315211)
潜艇是水下作战的主要武器,对潜艇的水动力特性进行研究有着一定的实用价值[1]。鉴于潜艇在水下时经常经历斜航和回转,可进行斜航和回转的实验,但这两种实验都只能获得同速度(包括线速度和角速度)相关的水动力系数,无法获得同加速度、角加速度相关的水动力系数[2-4]。为了获取同加速度、角加速度相关的水动力系数,需要对水平面和垂直面的运动机构进行试验,这就是平面运动机构试验(Planar motion mechanism,简称PMM)[5]。平面运动机构试验可在拖曳水池中进行,拖车上安装一支或两支振荡杆,通过调整振荡杆的振幅和相位,获取潜艇摇摆和振荡过程中的力和力矩,然后根据试验结果运用傅里叶展开获取与加速度、角加速相关的水动力系数。
国内外学者对潜艇操纵性及PMM试验的数值研究进行了大量的工作。Racine[6]基于重叠网格法模拟了扁平体水下航行器的斜航试验、回转臂试验和平面运动机构试验,求解了11个主要的水动力系数。Ahmad[7]、Hiroyoshi[8]以及Kim[9]等用计算流体力学(CFD)技术模拟了平面运动机构试验,并与水池中的试验结果进行对比,证明了数值模拟方法的可靠性。戴余良等[10]采用网格变形技术研究了全附体潜艇PMM的仿真试验,计算精度达到了工程应用的要求。吴兴亚等[11]对某民用打捞船进行了PMM数值试验并考虑了兴波和船模姿态的变化。高婷等[12]提出了一种求解水下航行器水动力系数的空间拘束运动模拟方法,并用平面机构运动试验证明了该方法的可靠性。刘义、邹早建等[13]采用CFD技术对三艘内河船舶在不同水深下的静舵试验、纯横荡和纯艏摇试验进行了数值模拟。
平面运动机构试验又分为水平面的平面运动机构试验和垂直面的平面运动机构试验。本文将结合潜艇的水下运动情况下对这两种平面机构的运动理论进行简单介绍,并采用重叠网格法进行PMM仿真实验,基于傅里叶变换和仿真数据,得到潜艇加速度和角加速度的方法,并计算了特定频率下潜艇的流场变化。
1 SUBOFF潜艇的模型参数
SUBOFF潜艇模型是美国国防高等研究计划署[14]设计的专门用于验证CFD计算准确性的标准模型。目前很多国家对SUBOFF模型进行了系统的水动力性能计算及流场的测试试验,其中最为详细且被广泛应用的是美国泰勒水池完成的试验,研究成果涉及速度、压力、摩擦阻力、雷诺应力以及水动力系数等一系列的试验数据。本文也将以SUBOFF全附体潜艇为计算模型进行仿真实验。
SUBOFF全附体潜艇由1个回转的裸艇体、1个指挥台围壳和4个呈十字形分布的尾舵翼组成,实际潜艇总长104.5 m,采用1∶24缩小模型。首部长1.016 m,平行中段长2.229 m,尾部长1.111 m,总长4.356 m。艇身最大回转直径为0.508 m。指挥台前缘位于艇体0.924 m处,指挥台长0.368 m,高0.46 m。尾翼后缘位于4.007 m处,呈十字形布置。SUBOFF的主尺度和几何模型见表1和图1。

表1 SUBOFF主尺度

图1 SUBOFF全附体几何模型(单位:m)
2 平面运动机构理论分析
2.1 纯横荡/升沉
潜艇纯横荡指潜艇在水平面内沿着中心线作匀速运动的同时叠加一横向位移,艇艏方向不变,潜艇无旋地作纵倾角为0的正弦运动。图2是纯横荡的示意图。

图2 纯横荡示意图
纯横荡的相关参数如式(1)所示:
(1)
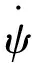
纯升沉的原理同纯横荡类似,区别在于从水平面变成了垂直面,潜艇在垂直面内沿着中心线作匀速运动的同时叠加一垂向位移,绕y轴的转角始终为0。图3是纯升沉运动的示意图。
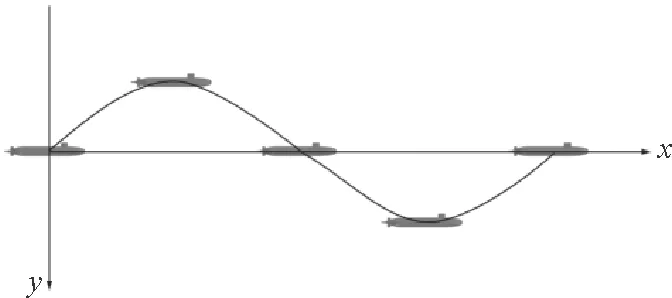
图3 纯升沉运动示意图
纯升沉运动的相关参数如式(2)所示:
(2)
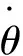
2.2 纯艏摇/俯仰
水平面的潜艇纯艏摇是指潜艇沿中心线匀速运动的同时叠加一个艏向角的变化,该艏向角使潜艇的运动轨迹时刻与艇体坐标系的纵轴(y轴)相切。图4是纯艏摇示意图。

图4 纯艏摇示意图
纯艏摇的运动参数如式(3)所示:
(3)

垂直面内纯俯仰的原理同纯艏摇类似,其速度方向始终与运动轨迹相切。图5是纯俯仰的示意图。
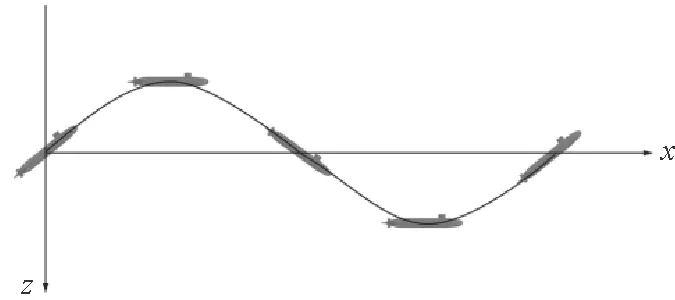
图5 纯俯仰运动示意图
纯俯仰的运动参数如式(4)所示:
(4)

3 PMM试验的数值实现
本节应用动态重叠网格法来进行潜艇PMM试验的计算。潜艇沿中心线作匀速运动的速度被等价为给定入口的流速,同时潜艇叠加一个振荡或摇摆,以此等价视为潜艇做PMM运动。PMM试验中惯性坐标系放置在艇的重心上,x轴正向指向艇艏,y轴指向右舷侧,z轴指向艇底,原点距离艇艏2.009 m。在惯性坐标系的基础上直接生成一个相同的坐标系,该坐标系即为斜航的艇体坐标系。
3.1 建立计算域
静止的背景区域(试验池)采用方形计算域,模拟拖曳水池。PMM试验的背景区域一般由以下准则确定:入口边界距离艇艏1.25倍艇长,出口边界距离艇尾2倍艇长,四周边界距离艇体1.25倍艇长。运动区域采用方块状,大小能够包络住整个艇体外形即可。
如图6所示对于纯横荡/升沉,潜艇分别在y方向和z方向上平移,因此,在潜艇作平移的范围内需要添加体网格加密区域,其网格尺寸应该与运动区域的网格尺寸保持一致。对于纯艏摇/俯仰,潜艇分别绕着z轴和y轴旋转的同时做上下或前后振荡,因此潜艇做平移叠加旋转运动的最大范围内同样需要体网格加密,且网格尺寸需要同运动区域的尺寸保持一致。

图6 各区域示意图
3.2 网格划分
两个区域均采用切割体网格。重叠网格的尺寸和背景网格在重叠区域的尺寸应保持一致,以确保交界面处插值计算的稳定;艇体周围和尾流部分应适当加密,保证周围流场拥有良好的分辨率。最终生成重叠区域网格数量约138万,背景区域网格约343万,总计约481万,如图7所示。

图7 截面网格
3.3 自定义场函数
平面运动机构的仿真试验中,潜艇沿中心线做匀速直线运动的速度被等价为计算域入口的流速,而潜艇做振荡或摇摆则通过区域的平移或旋转来实现,其中平移速度或旋转角度需要通过场函数来指定。对于纯横荡或升沉,需要指定其振幅a、圆频率ω以及平移速度(横向速度v或垂向速度w)。以纯横荡的振幅为0.3 m、圆频率为0.625π。纯升沉的场函数设置过程与纯横荡的完全一致。
对于纯艏摇或俯仰运动,不仅需要指定其圆频率ω、旋转角度(ψ或θ)以及最大旋转角度(ψ0或θ0),还需要指定艇体做艏摇或俯仰运动时的振幅。该振幅是由航速、最大旋转角度和圆频率共同确定。一方面艇体按照正弦规律左右或上下振动,另一方面则绕重心在水平面或垂直面内按正弦规律转动,这两种运动的合成就是纯艏摇或俯仰运动。以纯艏摇为例,其旋转角度为10°、圆频率为0.625π。
下一步需要生成与振荡相关的振幅a和振荡速度v,该振幅和速度需要区别于纯横荡或升沉的振幅和速度。振幅a的取值由航速、最大旋转角度和圆频率共同确定,分析纯艏摇的运动性质,振幅a的推导过程如下:

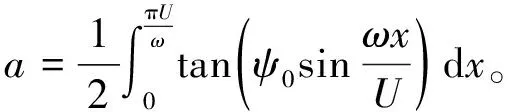
当频率f=0.312 5、最大旋转角度ψ=10°、航速U=3 m/s时,潜艇做纯艏摇的振幅a=0.133 9 m。
为了获得稳定的计算结果,通常计算4~6个运动周期,1个运动周期分为400个时间步,因此,当纯横荡的频率f=0.312 5 Hz时,运动周期T=3.2 s,时间步长为T/400=0.008 s,最大物理时间4T=12.8 s。其余频率依此类推。
4 后处理和数据分析
4.1 水动力系数
以纯横荡为例,分析其运动性质可以发现,纯横荡过程中产生的力和力矩包括与纯横荡同相的振荡部分和正交的振荡部分,其运动方程式可以简化为
(5)
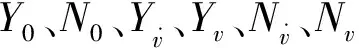
将式(1)中的运动参数代入式(5)中,则有
(6)
式中:a为纯横荡的振幅;ω为纯横荡的频率;t为时间。
将等号右侧无因次化,得到
(7)
式中:U为线速度;L为艇长;ρ为流体密度。
初始状态下,潜艇自身的力均为零,因此常数项可以省略,所以有
(8)
因而纯横荡运动可以求解的无因次水动力系数有
其余3个运动求解水动力系数的原理同纯横荡一致,在此不作过多赘述。需要注意的是,纯艏摇或俯仰涉及的水动力系数同角速度和角加速度有关,因此系数在无因次化得过程中分母要比纯横荡或升沉多一个L。
由于PMM运动属于非定常运动,速度和旋转角度是关于时间的周期函数,因此力和力矩也是关于时间的周期函数,不能同斜航和回转那样待计算收敛后得到一个稳定的力和力矩值,因此无法采用和前2种试验相同的数据处理方式。由PMM的运动性质可知,力和力矩采用正交分解的方法,可以分解为同向分量和正交分量,因此PMM的周期性数据可以通过傅里叶展开以获得准确的水动力系数。式(9)、(10)以纯横荡为例,简单阐述用傅里叶积分展开处理PMM数据的过程:
(9)
(10)
式中:f(t)为傅里叶积分函数;an、bn为积分系数;l为运动周期的一半。

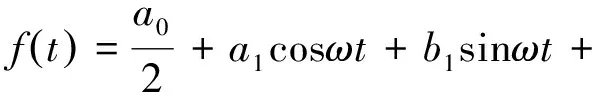
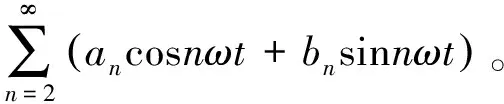
(11)
由于a1>>a2,b1>>b2,因此省略a2、b2项及后面的项,则有
(12)
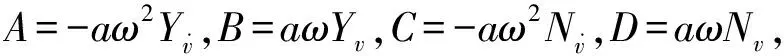
(13)
式(13)应用傅里叶积分展开定理得
(14)
(15)
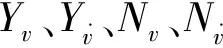
待PMM仿真对应的4~6个完整周期计算结束后,取稳定的最后一个周期或倒数第二个周期的401个计算值,将计算结果导出并处理,最终将处理后的数据以数值矩阵的形式导入Matlab进行积分,得到完整的A、B、C、D值后进行线性拟合,得到与PMM运动相关的水动力系数。
纯横荡或升沉中,航速U为3 m/s,振幅a为0.3 m,为了使得到的周期T易于计算,选取的频率f为0.2、0.25、0.312 5、0.4、0.5和0.625 Hz,对应的周期分别为5、4、3.2、2.5、2和1.6 s。纯横荡的傅里叶积分结果如表2所示。
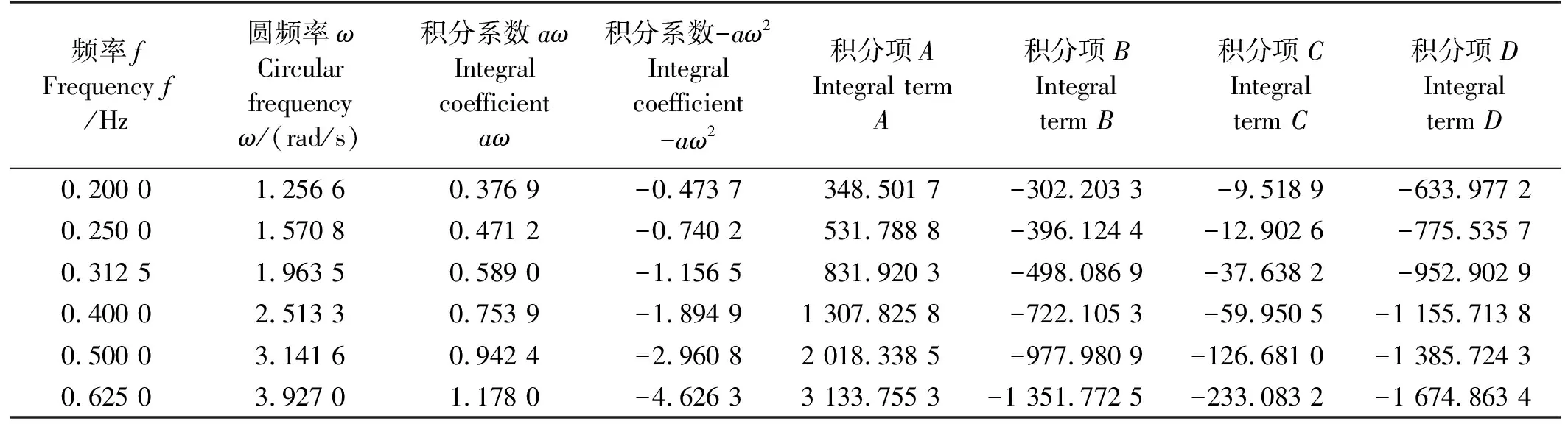
表2 纯横荡傅里叶积分结果
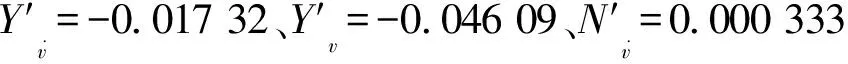
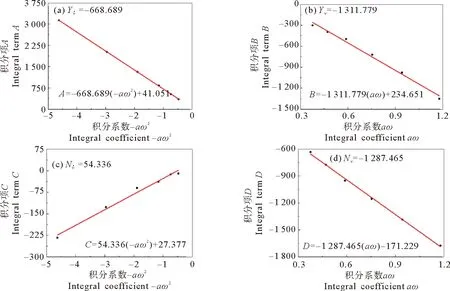
图8 纯横荡运动的拟合曲线
同理,将纯升沉的方程式应用傅里叶积分展开定理得
(16)
(17)
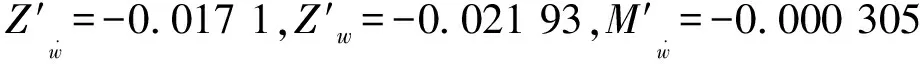

图9 纯升沉运动的拟合曲线
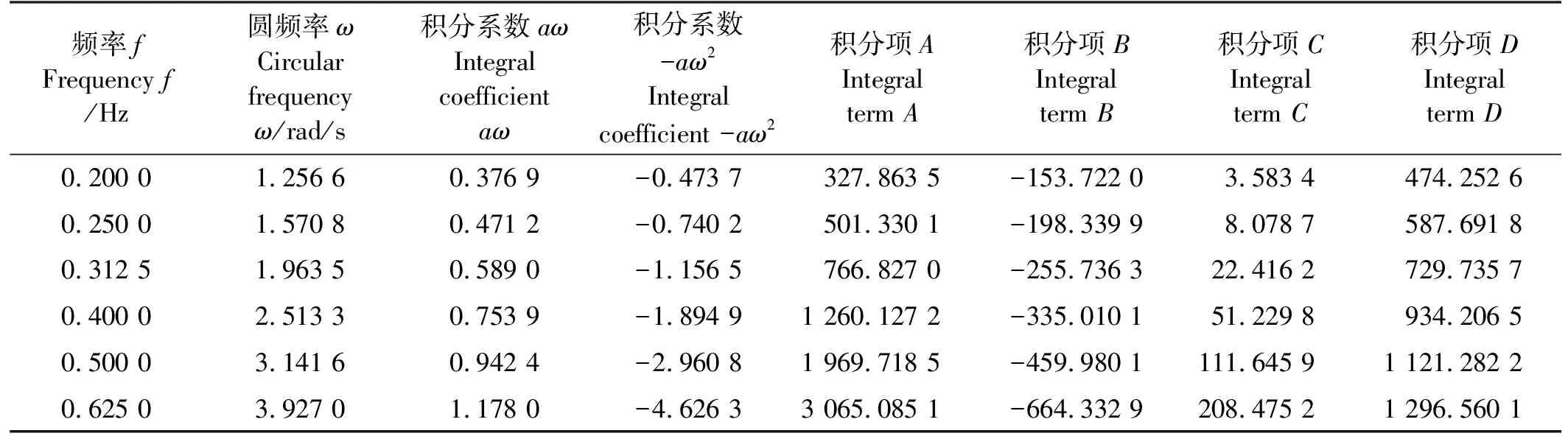
表3 纯升沉傅里叶积分结果
纯艏摇或俯仰中,航速U为3 m/s,最大旋转角度为10°,为了使得到的周期t易于计算,频率f同样选取为0.2、0.25、0.312 5、0.4、0.5和0.625 Hz,对应的周期分别为5、4、3.2、2.5、2和1.6 s。
将纯艏摇方程式应用傅里叶积分展开定理得
(18)
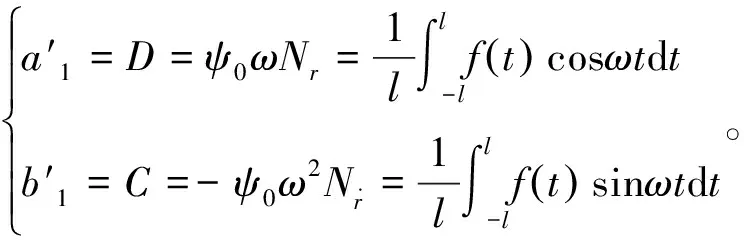
(19)
纯艏摇傅里叶积分结果如表4所示。
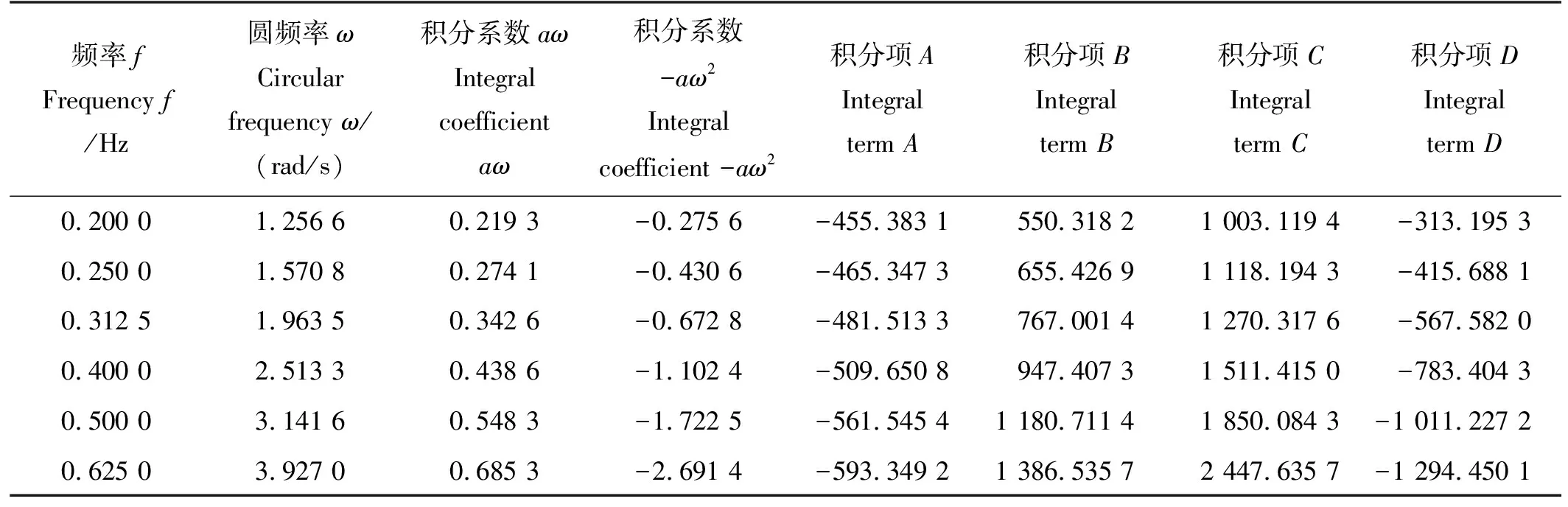
表4 纯艏摇傅里叶积分结果


图10 纯艏摇运动的拟合曲线
同样的,将纯俯仰的方程式应用傅里叶展开定理得
(20)
(21)
纯俯仰的傅里叶积分结果如表5所示。

表5 纯俯仰傅里叶积分结果
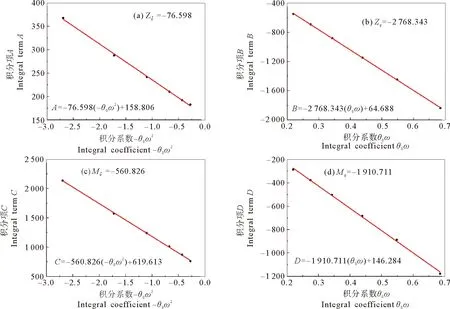
图11 纯俯仰运动的拟合曲线
美国泰勒研究中心做了SUBOFF全附体潜艇的操纵性试验,并公布了部分水动力系数试验数据[15]。表6、7将本文计算所得到的所有水动力系数列出,并与试验数据和其他2个约束模试验数据进行对比。
由表6可以看出,整体而言,PMM运动计算所得的惯性类水动力系数与试验值吻合较好,与力相关的(角)加速度系数误差明显比力矩相关的(角)加速度系数小。从运动性质上分析,振幅和摇摆角度对拟合曲线中的力和力矩影响不大,因为最终算得的水动力系数都进行了无因次化处理。但由于本文选取的PMM振幅0.3 m和摇摆角度10°均是较大的数值,因此在频率较大的情况下,潜艇所受的力和力矩会表现出强烈的非线性以及计算的不稳定性,从而对最终的拟合曲线和水动力系数带来较大的误差,这种较大的误差更明显的体现在表7的黏性类水动力系数中。除此之外,PMM运动所采用的数学模型是基于小振幅线性假设的,并没有考虑非线性项和耦合项的影响,这也是产生误差的重要原因之一。

表6 惯性类水动力系数
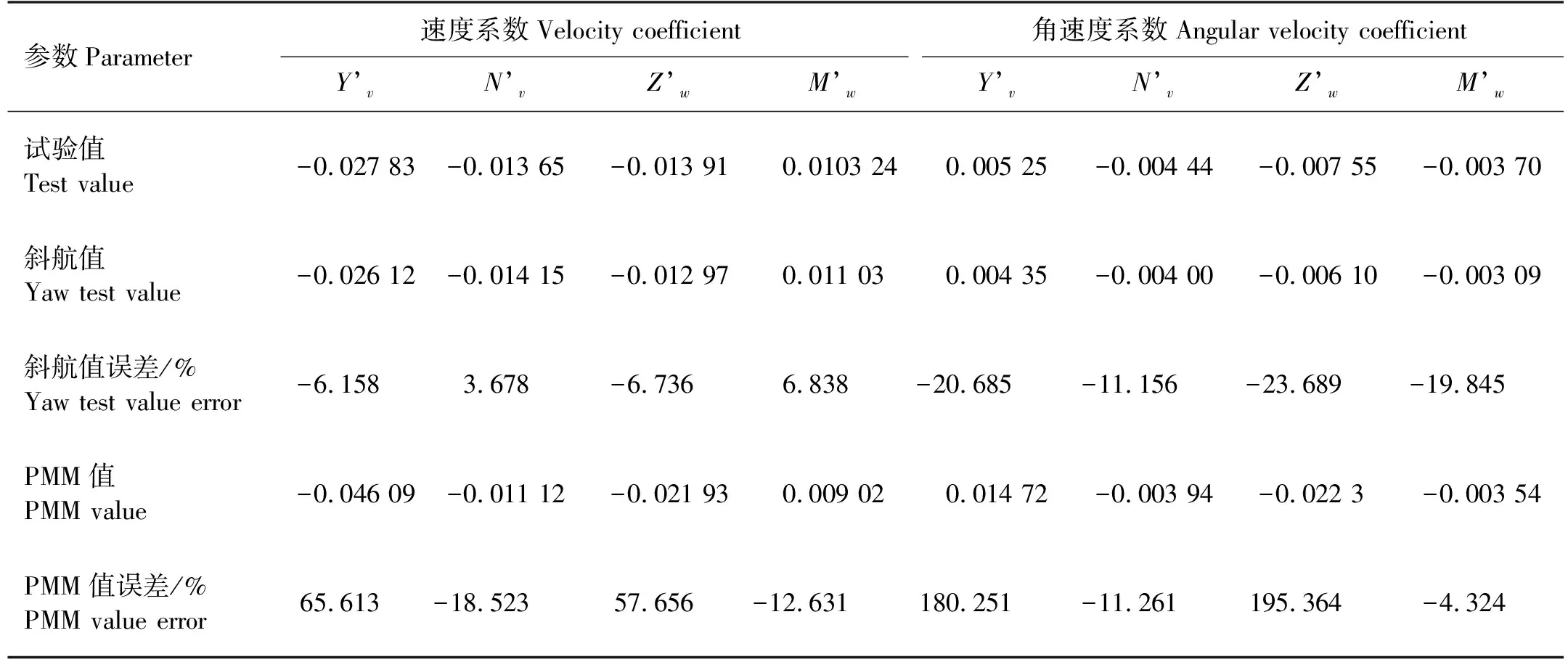
表7 黏性类水动力系数
由表7可知,部分黏性水动力系数(尤其是角速度系数)表现出了相当大的误差。从数值方法上分析,这与目前所采用的湍流模型对潜艇分离流的模拟精度可能仍然较差有关。当潜艇处于大攻角或大漂角的姿态下艇体和附体背流面均会产生明显的流动分离和一系列复杂涡系。当潜艇做纯横荡或纯艏摇时,潜艇姿态发生改变(偏移或旋转),其流动分离和涡系也会相应的发生偏移,涡量和附着涡系的动态变化在一定程度上影响了边界层厚度和流动,导致算例中的湍流模型适用性降低,从而产生了数值上的计算误差。
参考文献[16]的工作,在应用PMM试验求解线性导数的过程中,过原点拟合和不过原点拟合的结果有明显差异。本文的纯艏摇和纯俯仰曲线的线性部分明显不过原点,无疑会增大计算误差。PMM试验应进行多工况求解,并过原点进行线性拟合,获取拟合后的线性导数值。从线性理论出发,由多工况绘制的曲线应该具备过原点和近似线性变化的特征,因此在PMM形成振荡的数值预报技术中,其线性水动力导数的获取需要将原点考虑在内进行线性拟合。此外,工况数多寡也会影响线性导数的拟合结果,因此需设置较多工况进行拟合,尽量减小影响。
总而言之,虽然PMM试验可以将黏性类水动力系数从力和力矩中分离出来,但其受到各种原因的束缚,计算得到的精度明显不如惯性类水动力系数。但从计算效率的角度上看,一组PMM试验能够同时获得惯性类水动力系数和黏性类水动力系数,而斜航和回转试验需要多组漂角或攻角姿态和多组回转半径,因此PMM试验的计算效率明显高于斜航和回转。
4.2 流场结构
对于同一平面机构运动而言,频率的改变一般只会影响艇体的流动分离程度,对于整个流场结构的分布并无太大影响,同时由上文的拟合曲线可以看出,水动力系数与ω项呈现线性关系,两者之间的非线性程度较弱,因此本节只选取频率f=0.4 Hz时,4个平面运动剖面处的速度云图作为分析PMM运动流场结构的对象,其余频率不作讨论。
图12、13是纯横荡运动和纯艏摇运动在一个周期内4个典型时刻(t=T/4、t=T/2、t=3T/4和t=T)的中横剖面速度云图。由图12可以看出,潜艇在水平面做振荡或摇摆时,艇体周围的速度分布以半个周期为界限,呈现严格的对称性。当潜艇做纯横荡时,艇体进流段和去流段的肩部均会发生不同程度的速度跃升现象。当0 图12 纯横荡速度云图 图13 纯艏摇速度云图 纯艏摇中,前1/4个周期内潜艇艏向角由0°向左转到最大转角10°,率先接触水流的进流面(左舷)面积逐渐增大,导致从艇艏到左舷肩部的扇形低速区面积也越来越大,而背流面的肩部形成一个高速区。潜艇平行中段到去流段的向内收缩曲率也会引起一个速度差。左、右舷的速度分布不均引起了压力不均布,从而产生了周期性变化的侧向力和偏航力矩。潜艇从最大漂角回转到起始位置的过程中,左舷周围流场的速度值逐渐增大,直至t=T/2时形成一个拉长的倒马鞍形。纯艏摇后半周期的速度场变化同样与前半周期以中纵轴线呈对称分布。 图14 纯升沉速度云图 图15 纯俯仰速度云图 垂直面的平面运动机构相当于水平面翻转90°,因此其中纵剖面处速度云图的分布规律与水平面几乎一致,唯一的区别在于:垂直面在艇体进流段的上方多出了一个指挥台围壳,指挥台围壳跟随艇体一起做振荡和摇摆。潜艇在垂直面运动时,指挥台围壳后方会形成一道长长的速度拖尾,在潜艇向上平移和向下摆首的过程中该速度拖尾会逐渐贴近艇体直至融合,潜艇下浮和翘首时又会逐渐分离。这种现象会一定程度上改变潜艇周围流场的结构,但受到尺寸等因素的约束,总的来说影响并不会太大。 (1)整体而言,PMM运动计算所得的惯性类水动力系数与试验值吻合较好,与力相关的(角)加速度系数误差明显比力矩相关的(角)加速度系数小。部分黏性水动力系数表现出了相当大的误差。线性导数的预报同工况及数值模型的适用性等多因素密切相关。 (2)从计算效率的角度上看,一组PMM试验能够同时获得惯性类水动力系数和黏性类水动力系数,而斜航和回转试验需要多组漂角/攻角姿态和多组回转半径,PMM试验的计算效率明显高于斜航和回转。 (3)当潜艇纯横荡时,艇体进流段和去流段的肩部均会发生不同程度的速度跃升现象;纯艏摇后半周期的速度场变化同前半周期一样以中纵轴线呈对称分布;潜艇垂直面的平面运动机构相当于水平面翻转90°,因此其中纵剖面处速度云图的分布规律与水平面几乎一致,唯一的区别:垂直面在艇体进流段的上方多出了一个指挥台围壳,指挥台围壳跟随艇体一起做振荡和摇摆。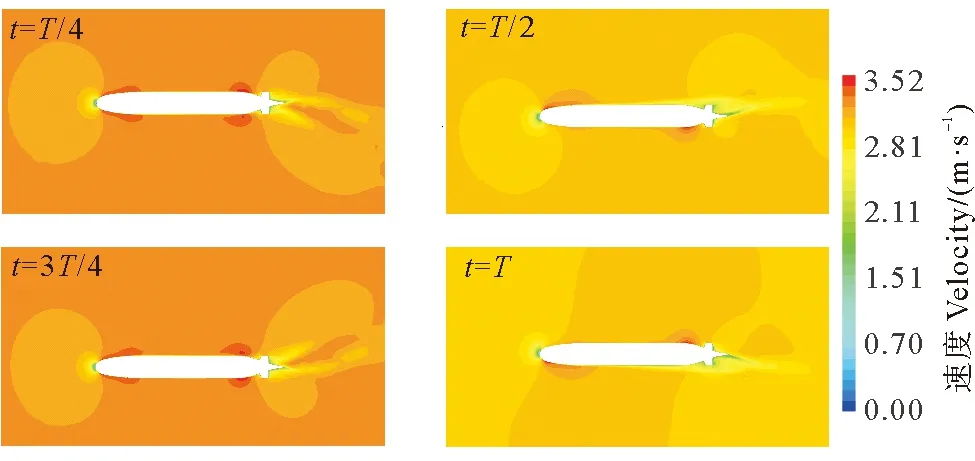



5 结论

