海表外强迫效应对连续层化流体中先驱内孤立波生成的影响❋

张静华，江文胜

(1.中国海洋大学环境科学与工程学院, 山东 青岛 266100；2.交通运输部天津水运工程科学研究院，天津 300456；3.中国海洋大学海洋与大气学院物理海洋教育部重点实验室, 山东 青岛 266100; 4.青岛海洋科学与技术试点国家实验室，山东 青岛 266237)

内孤立波是层化海洋中常见的现象，其现象丰富、机制复杂，尽管研究手段多样，但目前尚未完全认识清楚。传统观点认为，内孤立波主要由正压潮流和地形相互作用而产生[1-2]，但这种机制并不能解释所有的内孤立波生成。研究表明，一些其它机制如混合区塌陷机制、共振机制、西边界流不稳定机制等也可能引起内孤立波，其中共振机制解释的是沿着某一水平方向运动的外强迫，在接近临界速度条件时会向强迫上游周期性地生成内孤立波，外强迫可以作用于水体表面或水底。除了向强迫上游周期性地产生孤立波外，在强迫下游还会形成一个随时间发展的向下游方向延伸的等密度面的凹陷区(称为压水区)，以及紧随其后的一列弱非线性弱频散的尾波，这种机制生成的内孤立波被称为先驱内孤立波。考虑来自水面的外强迫时可能为海面移动的大气压异常，或者在海面航行的船舶；来自水底的外强迫则对应底地形起伏(如海山、海沟等)。

先驱孤立波现象最早在实验室中模拟船舶航行激发的表面波时发现，进而开展了一系列研究[3-7]。Zhu[8]、Grimshaw和Smyth[9]、Grimshaw和Yi[10]等参照表面波的研究方法将研究拓展到两层流体界面的内波，证明两层流体内界面上产生的先驱内孤立波与均匀流体表面产生的先驱孤立波具有相似的性质。在模拟先驱孤立波时，广义Boussinesq模型以及fKdV(forced KdV)方程模型(后者是在前者基础上限定外强迫只在某单一方向运动而得到，两者可归为一类)应用最为广泛，但是采用这类模型具有以下缺点：首先，广义Boussinesq方程和fKdV方程都是基于弱非线性、弱频散假设推出的，当内波振幅较大从而非线性变得显著时，采用弱非线性假定的模型结果并不可靠。其次，这类模型基于两层近似，跃层被简化为一条线，这与海洋中真实层结相差过大，会影响对跃层及其附近水体动力过程的认识。模拟先驱孤立波的另一思路是对动力学基本方程组Navier-Stokes方程进行数值求解，这样既可不受弱非线性和弱频散假设的限制，也能模拟连续层化的情形。Stastna等[11-13]采用欧拉方程模型(不考虑粘性时)模拟了层化流体流经起伏的地形时因共振产生的内孤立波，讨论了地形尺度、背景剪切流等的影响，还发现了第二模态内孤立波以及内波破碎等现象。这些研究显示了基于Navier-Stokes方程的模型在研究先驱内孤立波现象中的潜力，只是这类工作还较少，且只考虑了海底地形强迫的作用，缺乏水面强迫作为强迫来源的研究。

先驱内孤立波的产生和发展是外强迫与分层流体共同影响的结果，外强迫作为激发先驱孤立波的来源，是最重要的影响因素之一。在数值模拟中，对于表面强迫和海底地形这两种形式的外强迫是否等效，Wu等[3]从理论上分析了模拟先驱孤立波现象的forced KdV方程和forced Boussinesq两种典型模型的结果，发现两种强迫对于均匀流体并非完全等效。对于连续分层流体来说，这一问题更缺乏确定性结论，在研究中不宜将两者等效替代。外强迫的形态特征，如强迫的宽度、强度、作用方向等都或多或少地影响内孤立波的生成过程和波形特点[12,14-15]，其中强迫作用方向的不同对先驱孤立波产生的影响最为显著，且根据其影响规律可以将外强迫分为两类：正效应强迫和负效应强迫。规定当强迫作用方向与自由传播的内孤立波引起的等密度面位移方向相同时，该强迫被称为正效应强迫，反之则称之为负效应强迫。针对两层流体的研究表明，不论外强迫效应为正或负，在临界条件附近都可能产生先驱孤立波，但相对正效应强迫来说，在负效应强迫作用下，生成的孤立波之间较为分离，且生成周期大大增加[8-9]。已经证实在均匀流体中这一规律依然成立[3,5]，但在连续层化流体中，这一规律是否仍然成立，还具有哪些新的特点尚需进一步研究，是下一步需关注的问题。

综上，外强迫因共振而产生内孤立波的机制已经被证实是存在的，但针对这一机制开展的研究还并不完善，主要的不足包括：(1)现有对先驱内孤立波的研究结论主要是基于两层近似下的广义Boussinesq方程和fKdV方程获得的，可能受到弱非线性、弱频散假定的影响。(2)考虑连续层结流体中先驱内孤立波的研究还很有限，且多考虑海底地形的作用而没有考虑表面强迫的影响。为了深入研究连续层结流体中由海面的移动强迫引起的先驱内孤立波现象，克服因模型采用过多近似而产生的限制，本文采用一个三维的全非线性、全频散的非静力模型，针对海面压强强迫引起的先驱内孤立波进行模拟，并针对连续分层流体讨论外强迫效应的影响。

1 模型介绍及配置

1.1 NHWAVE模型简介

本文采用NHWAVE(Non-Hydrostatic WAVE)模型[16-18]，其动力学框架基于不可压缩流体的雷诺方程，可以给出任意时刻三维空间内的各物理量，适用于多层连续层结流体，同时不受弱非线性、弱频散性的限制。它既可以模拟波的反射、折射、浅水效应等各种近岸波动过程，还可以加入随时间变化的底地形，从而模拟海底滑坡引起的海啸波等现象。Ma等[19]将模型计算拓展到斜压流体中，增加了对密度和泥沙输运方程的求解。该模型还被Shi等[16]用于模拟哥伦比亚河口处内水跃的形成以及落潮时形成的“盐指”现象，并由Zhou等[20]用于研究层结流体中的剪切不稳定现象。

NHWAVE采用一种修正的C网格，空间离散采用有限体积和有限差分结合的方法，其中对动量方程采用Godunov格式进行有限体积离散，对动压泊松方程采用中差法进行离散，空间离散具有二阶精度。时间上采用二阶SSP(Strong stability-preserving)龙格—库塔格式进行离散，数值稳定性很好，并具有二阶离散精度。非静力计算中动压泊松方程的求解采用了高性能预处理程序库hypre(1)hypre是一种针对大型线性方程组进行高效求解的程序库，适用于大规模的科学计算，且该程序库具有高度的可移植性。更多信息可见官方网站https://computing.llnl.gov/projects/hypre-scalable-linear-solvers-multigrid-methods。中的高效线性方程求解器，模式又结合Shi等[18]提出的PDI(Pressure decimation and interpolation)方法，大大提升了斜压情景下非静力计算的效率，这使得在模拟需要较高分辨率才能表达的小尺度现象时，NHWAVE相比于其它模型更具优势。

1.2 模型配置

本文围绕海表面以临界速度运动的压强强迫在连续分层流体内激发内波的过程开展理想实验。计算在x-z二维平面开展，水平长度为20.48 km。计算域设为平底，静水深为100 m。水平分辨率5 m，水平网格数为4 096个，垂向采用σ坐标均匀地分成50层。初始场设为具有单一密度跃层的层化流体，并假设密度在水平向是均匀的，因此可用密度垂向剖面表征层化特点，由以下分段函数给出:

(1)

式中深度ds是密度跃层垂向剖面的转向点，本文定义为跃层深度。

在水体表面x0= 4 km处施加一个固定形状的压强强迫，并设置该强迫始终沿着x轴向左匀速移动，速度大小为Um。先驱内孤立波的产生和发展过程主要集中在外强迫附近，因此采用与外强迫同步运动的相对坐标系：在每一个时间步内，初始坐标系与强迫同步运动。因此在该运动的坐标系中，强迫始终处于初始位置，设置该初始位置为运动坐标系的原点，压强强迫在x轴上的分布满足

(2)

式中：X=(x-x0)-Um·t为运动坐标系中的位置坐标；P是水面压强强迫(单位为m，可理解为逆气压效应引起相对静止水面的凹陷或抬升)；l代表施加强迫的范围。采用随强迫同步运动的相对坐标系，方便对比强迫附近的波动，且可以利用有限的水平计算域模拟无限空间内的波动生成及演变过程，从而节省了计算资源。

为了使讨论的结果更具一般性，引入变量的特征值，将所讨论的要素进行无量纲化。水平空间变量采用特征宽度λ进行无量纲化。λ是根据两层KdV理论估算的内波波长。

(3)

式中：h1=ds；h2=h-ds；a取外强迫的强度。垂向特征长度为静水深h。时间变量用λ/c0进行无量纲化，第一模态内波自由传播的速度c0，也根据KdV理论给出：

(4)

其中g′为约化重力。由此，可以获得如下的无因次关系：

(5)

后文实验结果的分析及讨论将针对以上无量纲变量开展。

计算域的表层及底层边界均取滑动边界条件，东、西两侧边界取周期性边界条件，以避免边界反射波的影响。为了尽量避免由于采用周期边界条件而造成上、下游波动在传播至边界时相互影响，计算域在东西向上已经尽量加长。这里不考虑底摩擦效应的影响，且湍粘性项和扩散项的值取为零。试验计算时长均不少于20 000 s。

海洋中的跃层通常出现在上层，但对某些海区也存在季节性的深跃层甚至双跃层现象。这里设置层结的分布为海洋中典型的单跃层分布形态，分别针对跃层深度偏上和偏下两类情形进行试验，讨论海面强迫效应的正负造成的影响。当上层厚度小于下层厚度时，理论上只能存在下凹型内孤立波；当上层厚度大于下层厚度时，理论上只能存在上凸型内孤立波。根据跃层深度和压强强迫作用方向的不同，强迫效应的划分存在四种可能性(见图1)。上层厚度小于下层厚度时，压强强迫为正(或负)值，对应正(或负)效应，如图1(a)(或图1(b))所示；上层厚度大于下层厚度时，压强强迫为负(或正)值，对应正(或负)效应，如图1(c)(或图1(d))所示。

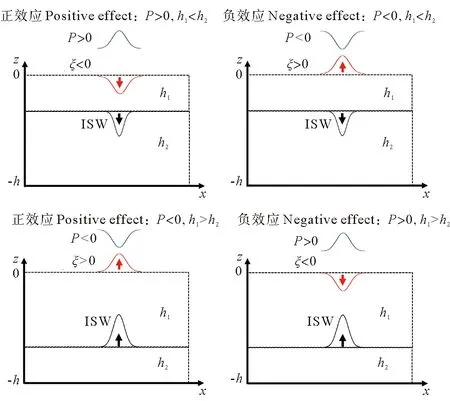
(P代表压强强迫，ζ代表强迫作用产生的海面起伏，h1和h2分别代表跃层上下的厚度。P represents the sea surface pressure forcing；ζ represents sea surface elevation caused by external force.h1 and h2 represent the thickness of the upper and lower layers, respectively.)

表1 试验参数设置

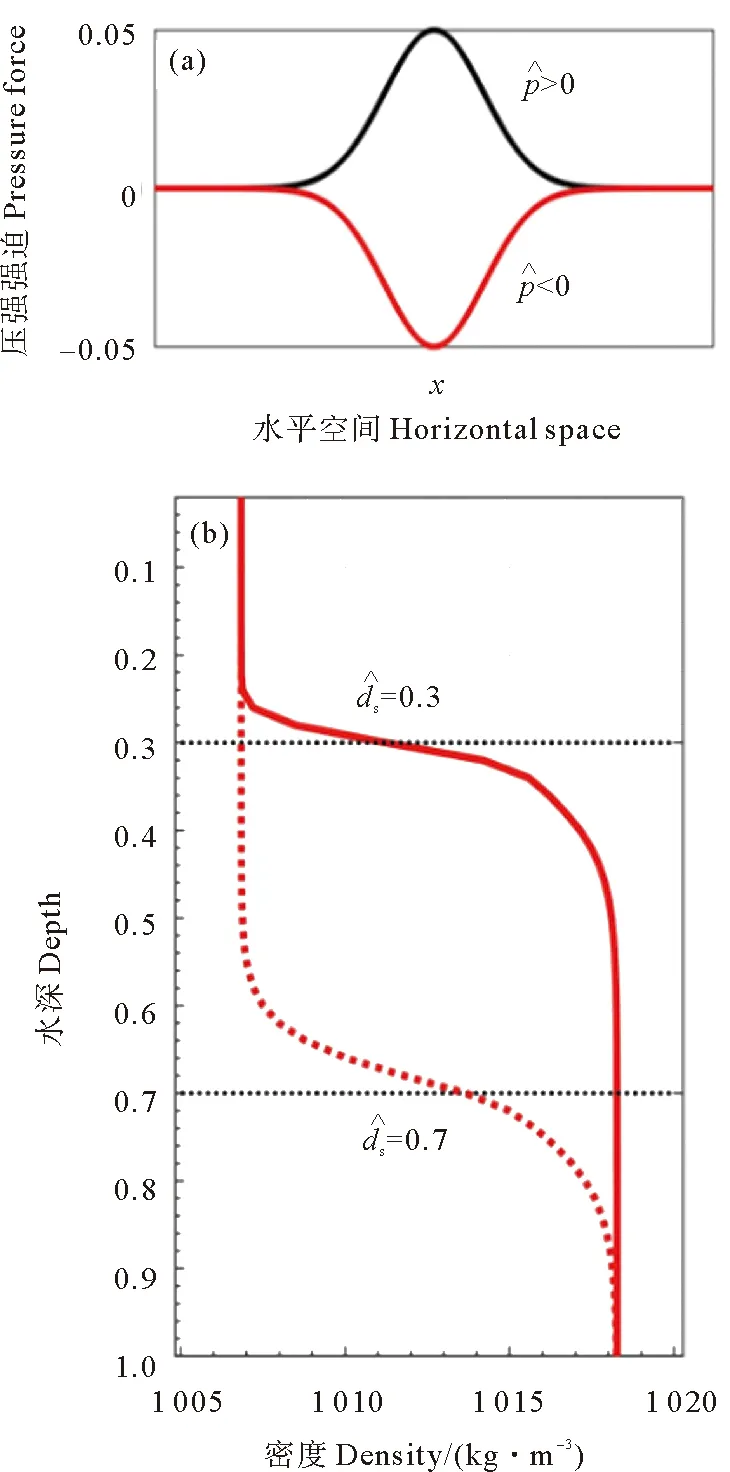
图2 外强迫分布(a)及密度剖面(b)

2 结果

2.1 跃层偏上时不同效应外强迫引起的先驱内孤立波

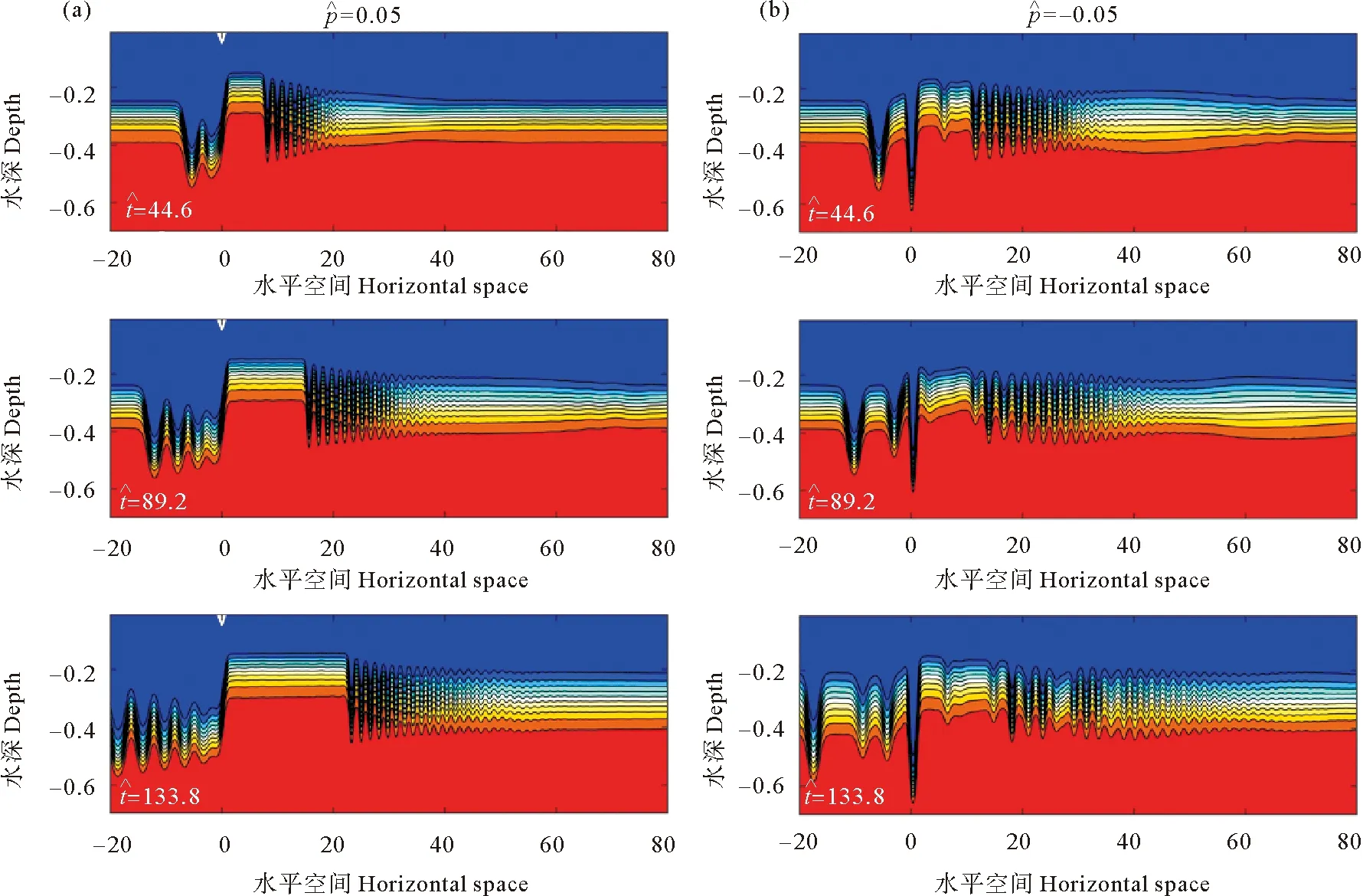
图5 跃层偏上时不同效应强迫作用下密度场的演变

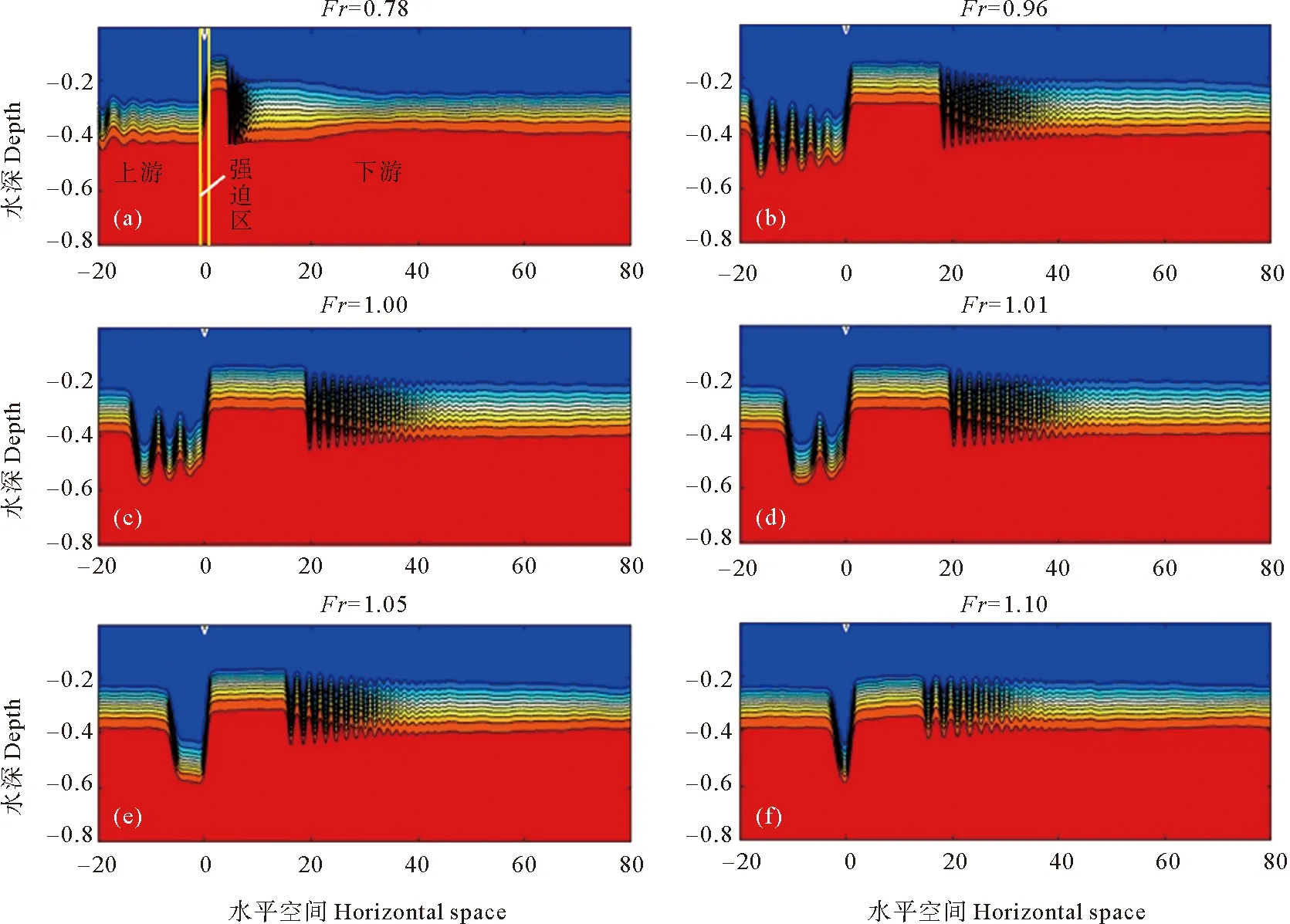
(图(a)对强迫区及对应的上游、下游进行了标注。For the convenience of readers, figure(a)annotates the forcing area and the corresponding upstream and downstream region.)

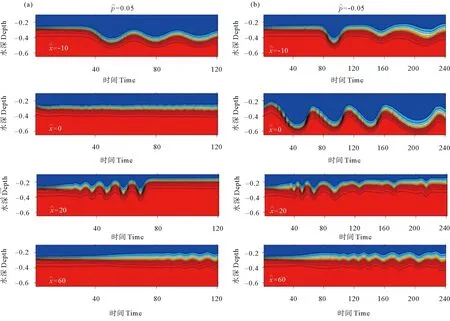
图6 跃层偏上时不同效应强迫作用下四个断面的时间序列

外强迫引起的内波也会相应地影响流场的结构。传统两层模型中流速在垂向上仅存在两个间断值，本文连续分层设置下可以更细致的刻画流场分布。以上游第一个产生的先驱内孤立波为例分析其流场结构。图中水平流速为相对坐标系中的流速。图7(a)和(b)分别对应正效应强迫时的水平流速和垂向流速，图7(c)和(d)对应负效应强迫时的水平流速和垂向流速。可见先驱内孤立波所在的位置将引起显著的流速，水平和垂向流速分量的大小接近0.5和0.1。受到内孤立波连续生成的影响，孤立波传播方向后侧的流速略大于前侧的流速。以跃层所在位置为界，水平流速呈现上下反向的结构，其中上层流速与内孤立波传播的方向一致，下层流速则相反，因此在垂向上形成速度剪切。以内孤立波中心为界，垂向流速主要呈现左右相反的结构，在水平向形成流速剪切。在本文连续分层下，可获得跃层内流速结构，在跃层内部，流速矢量形成闭合的回流，并呈逆时针流动。综合来看，两种强迫作用下的流场结构较为一致，但负效应强迫作用下水平流速的对称性更差一些，且流速偏小。

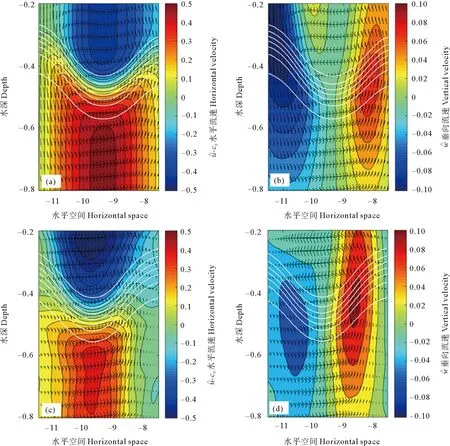
((a)和(b)对应正效应强迫作用下的水平流速和垂向流速分布，(c)和(d)对应负效应强迫作用下的水平流速和垂向流速分布。颜色代表相应的流速分量大小，矢量代表总流速，白色曲线代表等密度线。(a)and(b)show the distribution of horizontal velocity and vertical velocity under positive effect forcing, respectively.(c)and(d)show the distribution of horizontal velocity and vertical velocity under negative effect forcing, respectively.The colors indicate the magnitude of velocity components.The vectors indicate the direction velocity.The white curves represent the isopycnals.)

2.2 跃层偏下时不同效应外强迫引起的先驱内孤立波

图8 跃层偏下时不同效应强迫作用下密度场的演变

类似图6，图9显示了跃层偏下时四个相同位置断面的时间序列。对于跃层深度不同时两种正效应强迫情形(见图6(a)和图9(b))，各个区域内等密度面起伏的规律类似。结合图9(a)和图8可见，对于跃层偏下的负效应强迫情形，除了在上游难以产生先驱内孤立波，压水区和尾波区内的波动仍然可以产生并发展，只是它们的产生和传播速度都显著变慢。

图9 跃层偏下时不同效应强迫作用下四个断面的演变

由于在负效应强迫作用下，模拟时间内并未产生先驱内孤立波，因此图10只给出了正效应强迫下第一个内孤立波对应的流速分布。水平流速分量在垂向上的正、负分布规律，以及垂直流速分量在水平向的正、负分布与跃层偏上时相反，但流速的分布与内孤立波波形的关系对应则是相同的，可见在连续层结流体下，对于跃层深度不同的情况，根据正效应强迫和负效应强迫对其分类仍是适用的。对于相同效应的强迫，内波生成和演变规律以及流场性质可以类比得到。

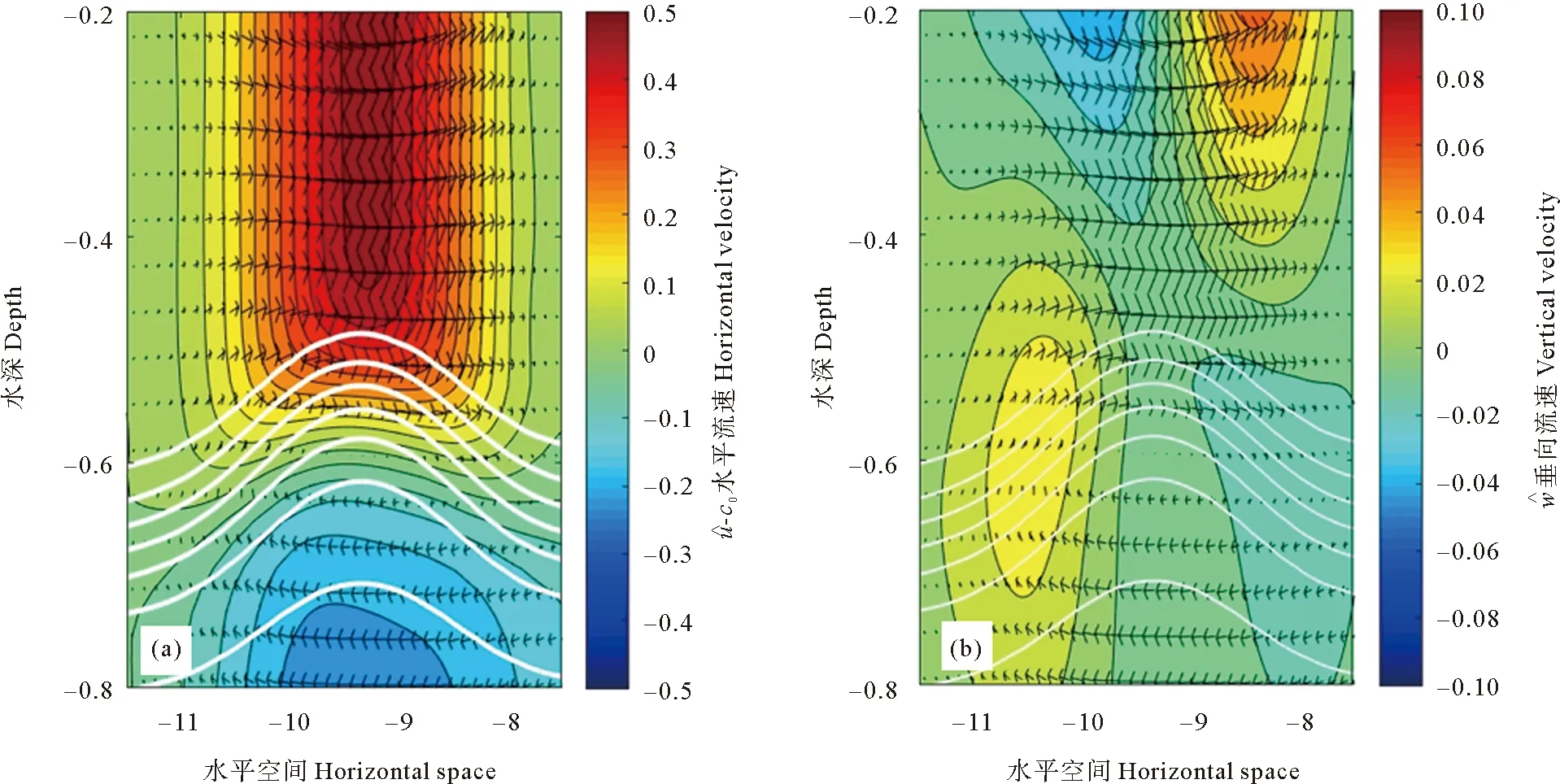
((a)水平流速分布，(b)垂向流速分布。颜色代表相应的流速分量大小，矢量代表总流速，白色曲线代表等密度线。(a)Horizontal velocity，(b)Vertical velocity.The colors indicate the magnitude of velocity components.The vectors indicate the direction velocity.The white curves represent the isopycnals.)

3 讨论

3.1 强迫效应正负对强迫区的影响

试验发现，在正、负效应强迫作用下，强迫区域内差异特别显著，这点在之前先驱内孤立波的研究中尚未明确提出。尽管Zhu[8]采用两层fKdV模型进行的数值试验结果也显示了正、负效应压强作用下强迫区内不同的响应，但是文中并未对这一特点进行说明，可能因其试验中波动振幅较小，这一差异并不显著。Grue等[21]曾提出，KdV理论仅在内孤立波振幅与内波垂向空间特征尺度(以跃层为界取上、层中较薄那一层的厚度来代表)的比值小于0.4时适用。由本文跃层偏上(见图5)和偏下(见图8)时这一比值约为0.6和0.4可知，对于本文算例来说，内孤立波的非线性都比较强。

强迫区内等密度面的差异也相应地影响流场的分布，特别是在跃层偏上时，跃层内等密度面随时间具有显著变化。分别对比强迫效应为正和负时多个时刻的流场分布。由图11可见，强迫区内流速的分布形态差异显著。在正效应强迫作用下，由图11(a)～(e)可知，强迫区内流速的结构基本不变，只是流速大小随时间变化有所变化。流速最大值靠近强迫区两侧边缘，强迫中心对应流速的小值。在跃层上下厚度较薄的那一层中，流速从中间指向两侧，形成速度辐散区；在负效应强迫作用下，由图11(f)～(j)可知，强迫区内流速整体更大，且形成了中间流速大，两侧流速小的分布结构。流速矢量在靠近中心的跃层附近维持逆时针的回流结构。随着时间演变，流速的大值区位置左右摆动，与该位置处的等密度起伏形态有关。

((a)～(e)对应正效应强迫情形，(b)～(d)对应负效应强迫情形。颜色和箭头分别表示总流速的大小和方向，白色线代表等密度线。(a)～(e)correspond to positive effect forcing,(f)～(j)correspond to negative effects forcing.The color and vectors indicate the magnitude and directions of velocity, the white curves represent the isopycnals.)

4 结语

本文采用一个全非线性、全频散的非静力模型NHWAVE，模拟连续分层流体中水面强迫引起的先驱内孤立波现象，并针对外强迫效应的影响开展研究，针对跃层偏上和偏下两种情况分别讨论。主要结论如下：

在连续分层流体中，外强迫效应的正负对波动形态有显著的影响，负效应强迫下先驱内孤立波的生成周期增大一倍以上，孤立波之间更为分离，与两层流体中的规律相同；在两种效应强迫作用下强迫区内的区别显著。当强迫效应为正，强迫区内水体的等密度面维持较稳定的结构，而当强迫效应为负，强迫区内水体的等密度面随时间发展起伏较大，对应地流场分布也更为复杂，在跃层内部及其附近区域，流速的结构差别也十分明显，在负效应强迫作用下，强迫区对应的跃层附近形成逆时针的回流区。

致谢:感谢美国特拉华大学史峰岩教授在数值模型调试方面提供的帮助。