采用单分类方法的行星滚柱丝杠故障检测

牛茂东， 马尚君， 蔡 威， 张建新,， 邓文竹

(1.西北工业大学 机电学院， 西安 710072； 2.江山重工研究院有限公司， 湖北 襄阳 441057)

0 引言

行星滚柱丝杠(planetary roller screw mechanism,PRSM)以其承载能力强[1]、精度高[2]、极限转速高[3]等优点，已逐渐成为机电作动器执行机构的最佳选择之一。PRSM结构如图1所示(可参考网站http://rollvis.com/swiss)，主要由丝杠、滚柱、螺母、保持架和内齿圈组成，其中丝杠和螺母均为多头螺纹，滚柱为单头螺纹，两端的保持架用于支承多个滚柱圆周均布，滚柱两端加工有直齿，分别与固连于螺母内部的内齿圈啮合。

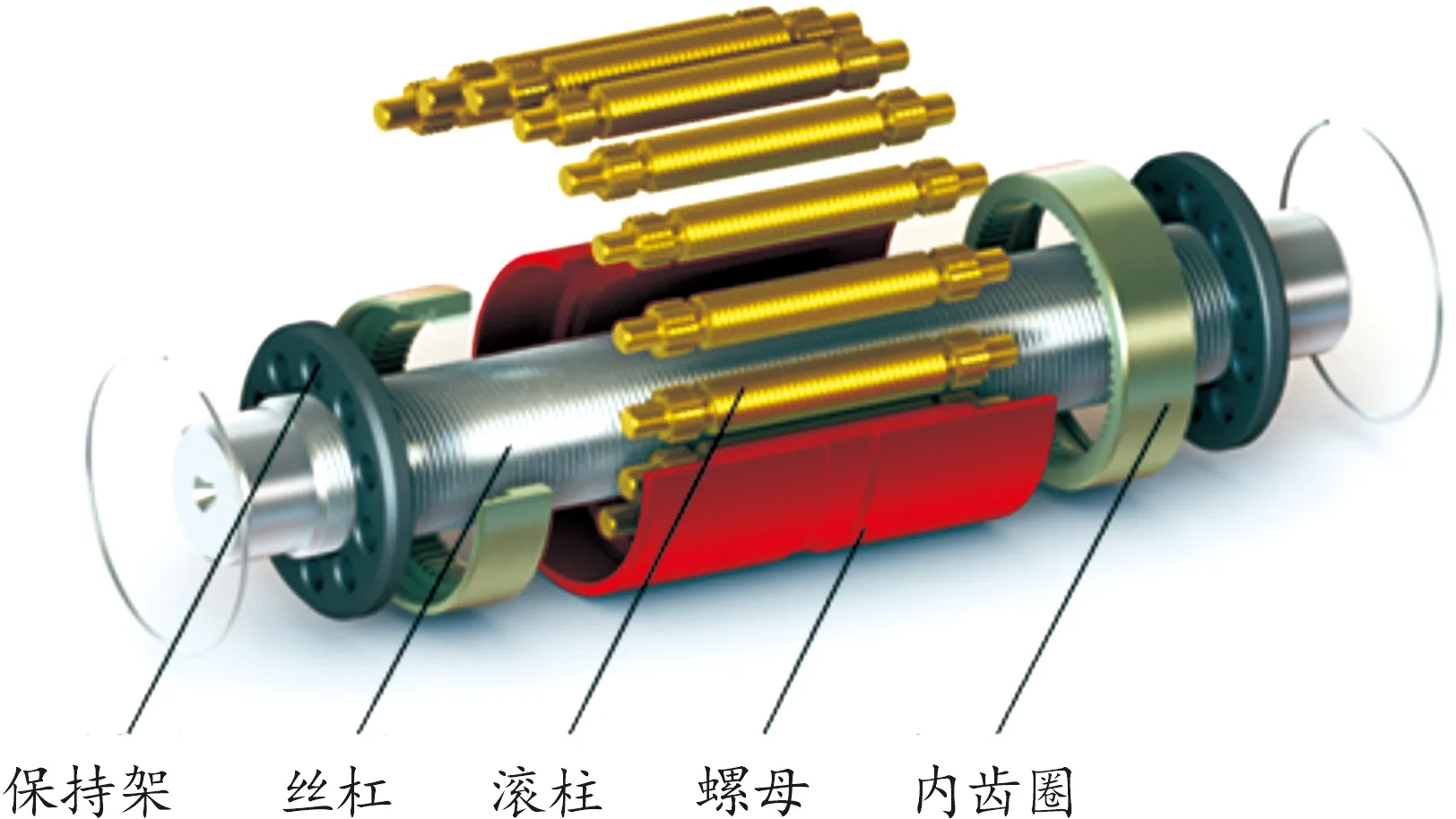
图1 PRSM结构示意图

目前针对PRSM的研究主要集中在载荷分布[4-5]、啮合原理及接触特性分析[6-7]、动态特性分析[8-9]等方面。近年来，PRSM在航空、航天、航海等领域以及一些要求精密伺服传动场合的应用逐渐增多，但是PRSM通常以机械单余度的形式存在，其可靠性决定了整个系统的可靠工作，故迫切需要对PRSM的故障诊断方法进行研究。目前的故障诊断方法大多针对齿轮箱、轴承和电机等对象，如梁敏健等[10]利用长短期记忆网络对门座式起重机减速箱进行了故障诊断研究。Hwang等[11]利用支持向量机对轴承进行了故障诊断研究。上述方法均需要对故障状态的齿轮箱或轴承进行试验以采集数据，而某些故障状态的齿轮箱或轴承运行时有一定的安全风险甚至无法运转。基于上述情况，刘广孚等[12]将单分类支持向量机(one-class support vector machine,OCSVM)模型用于区分潜油电泵的正常状态和异常状态。李凌均等[13]将支持向量数据描述(support vector data description,SVDD)方法用于水泥厂煤灰鼓风机故障诊断的工程实践中。对于PRSM，虽然Niu等[14]使用BSA-SVM方法对PRSM进行了故障诊断研究，但只考虑了一种故障状态，故障种类少，而且出现新故障时，需要重新训练模型，未解决故障数据采集难和故障样本数量少导致的诊断不准确的问题。

现阶段PRSM存在故障机理不明或故障种类少的问题，若仅利用已有故障类型建立故障诊断模型，当出现新故障时则无法准确判断故障类型。针对该问题，采用单分类模型进行故障检测，判断PRSM是否发生故障，提出了一种基于deep SVDD的PRSM故障检测模型，采用PRSM正常状态数据训练模型，然后用测试集进行测试，完成PRSM正常与故障状态的判断。其中，训练集中正常状态的数据是PRSM在试验台上正常运行时采集得到的数据，测试集中既包含正常状态的数据，又包含故障状态的数据，故障状态数据包含实际使用过程中出现的润滑失效和滚柱一侧断齿的故障数据。

1 基础理论方法

1.1 SVDD理论

Tax等[15]在2004年提出了SVDD的单分类模型，用于区分目标样本和非目标样本，假设目标样本x∈Rn×d。，其中n是样本数，d是特征维度，输入x通过非线性映射函数，将输入映射到输出空间，然后在特征空间中构建一个超球体，将尽可能多的目标样本包含在内，SVDD的目标函数如下：

(1)

约束条件：

式中：c为超球体的中心；R为超球体的半径；ζi为松弛因子；λ为用于均衡超球体的体积和误差。利用拉格朗日乘子法更新上述目标函数，上述目标函数表示为：

(2)

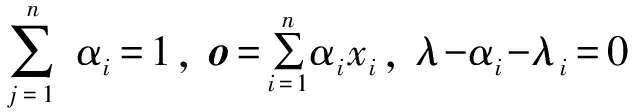
(3)

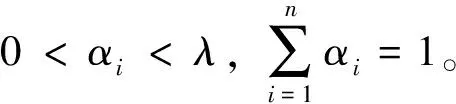
对于测试样本y，如果满足式(4)，则为目标样本，如果相反，则测试样本y为非目标样本。

(4)

以上计算存在x和xi的内积项，因此可以通过用与某些映射函数φ相对应的核函数代替内积项，实现输入空间到高维特征空间的映射，如〈φ(xi),φ(xj)〉=K(xi,xj)，此时式(3)可以表示为：

(5)

代表性的核函数及公式如下[16]：

1)径向基核函数

(6)

式中：c=2×σ2，σ为尺度参数。

2) Sigmoid核函数

K(xi,xj)=tanh(β0〈xi,xj〉+β1)

(7)

式中：β0为标量；β1为位移参数。

3) 多项式核函数

K(xi,xj)=(1+〈xi,xj〉)p

(8)

式中：p为多项式核函数的最高项次数。

c、β0、β1、p为核函数的参数，依据经验选择。

1.2 deep SVDD理论

Ruff等[17]在2018年提出了deep SVDD，其原理如图2所示，该模型使用神经网络提取特征，将数据映射到最小体积的超球体内，对SVDD计算可扩展性差、难以应用于高维数据的缺点进行改进。

图2 deep SVDD原理示意图

如图2所示，deep SVDD是基于传统SVDD的一种深度学习单分类算法，神经网络通过非线性映射使绝大部分目标样本落在一个中心为c，半径为R，最小且封闭的超球体内，这个超球体要在尽量小的前提下包含尽可能多的目标样本，测试时通过数据是否落在构建的超球体内判断一组给定的样本是否是目标样本，与传统SVDD的核函数提取特征不同，deep SVDD利用神经网络来提取特征。deep SVDD的目标函数如下：

(9)

deep SVDD使用异常分数s来评估模型，异常分数s为测试样本xt到超球体中心的距离，公式为：

(10)

deep SVDD构建了一个以c为中心的最小体积的超球体，通过一个二次损失来惩罚输出φ(xi;W)到超球体中心c的距离，并通过最小化所有数据表示到超球体中心的平均距离来缩小超球体，为了将数据映射到尽可能靠近超球体中心的位置，构建的神经网络必须能够提取目标样本的公共特征。

2 基于deep SVDD的故障检测方法

2.1 基本流程

基于deep SVDD理论的PRSM故障检测流程主要由数据处理、训练阶段和测试阶段组成，详细流程如下：

1) 对正常状态和润滑失效及滚柱一侧断齿2种故障状态的PRSM进行故障试验，采集各状态的振动数据；

2) 对数据进行归一化，并通过窗口裁剪的数据增强方法增加样本数量；

3) 使用小波包变换的方法对信号进行小波包分解，将系数矩阵作为后续的输入；

4) 构建神经网络，用只包含正常状态数据样本的训练集，通过多轮迭代完成神经网络的训练，最终完成deep SVDD模型的训练；

5) 使用包含正常和故障状态的PRSM数据样本的测试集对训练好的deep SVDD模型进行测试。

基于deep SVDD的故障检测流程如图3所示。

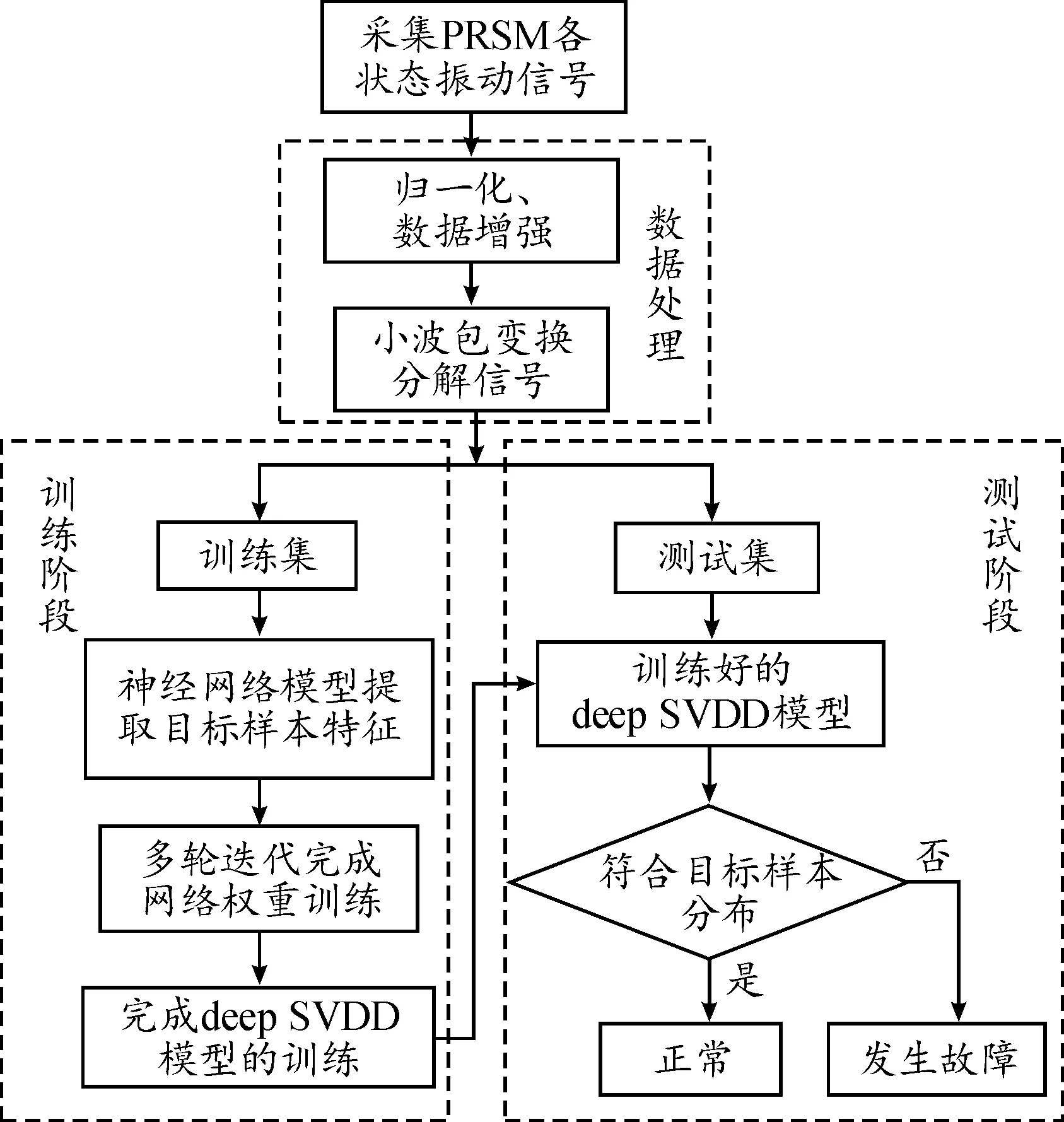
图3 基于deep SVDD的PRSM故障检测流程框图

2.2 评价指标

为了测试训练得到的模型，使用测试集对其进行测试，其中测试集既含有正常状态的样本，也含有润滑失效和滚柱一侧断齿的样本，而且每种状态的样本数相同，正常状态的样本总数少于故障状态的样本总数，存在样本不平衡的问题，此时准确率无法很好地评估模型，所以选择的评价标准为ROC曲线下面积(area under the receiver operating characteristic，AUROC)，AUROC的计算方法同时考虑了模型对于目标样本和非目标样本的分类能力，在样本不平衡的情况下，依然能够对模型做出合理的评价，成功规避了样本不平衡带来的问题。

3 方法验证

3.1 故障模拟试验

为了验证提出的故障检测模型在PRSM故障检测中的有效性，使用PRSM试验台采集各状态的振动信号，PRSM试验台如图4所示，主要由伺服电机、联轴器、被测PRSM和液压加载系统等组成。

图4 PRSM试验台

分别设置了PRSM正常、润滑失效和滚柱一侧断齿这3种工作状态，如图5所示。

图5 PRSM 3种工作状态

被测PRSM丝杠直径为24 mm，螺距为2 mm，头数为5，滚柱个数为10。受有效行程的限制，丝杠无法一直沿同一方向长时间旋转，所以采取丝杠正反转，螺母往复直线运动的方式，除换向阶段，螺母的直线速度为大小相同但方向相反的恒值，螺母伸出和缩回时的负载不同，所以负载在一定范围内波动，其中给定的载荷为实际载荷的最大载荷。丝杠转速设定为104 r/min，给定载荷为9 kN，加速度传感器安装在PRSM的螺母上，用于采集PRSM运行时的振动信号，采样频率为 20 480 Hz。

3.2 数据处理

3.2.1原始数据介绍

PRSM每种状态数据量为550 000，3种状态下的Z方向(垂直于螺母轴线并且平行于螺母端面)的振动加速度数据时域波形图如图6所示。

图6 PRSM 3种状态时域波形图

如图6所示，PRSM 3种状态下的时域数据无明显的规律和特征，其中润滑失效和滚柱一侧断齿2种状态的幅值相差较小，但是正常状态部分数据的幅值较大，存在较多噪声。

3.2.2数据归一化

将原始数据按式(11)进行归一化处理以减小数据跨度，由于加速度数据为矢量，存在方向性，所以采集到的数据有正有负，为了保留数据的方向特性，将数据归一化到[-1,1]之间。

(11)

式中：x为输入；M为自定义的最大值，此处取1；m为自定义的最小值，此处取-1。

3.2.3数据增强

通过窗口裁剪的方式进行数据增强，即通过一个固定大小的窗口，以固定的步长在一维数据上不断滑动来获得多组数据，具体实施过程如图7所示。

图7 窗口裁剪过程示意图

如图7所示，对数据进行重复采样，可获得多组不同的子数据，有效扩充了样本数量。获得的样本数量如下：

(12)

式中：p为获得的样本数量；n为原始数据总数；w为窗口尺寸；s为步长。

3.2.4小波包变换

PRSM的振动信号为非平稳信号且存在瞬间振动冲击，所以采取时频域分析——小波包变换方法提取数据特征[18]。

小波包变换的正交尺度函数φ(t)(低频分解)及其相对应的小波函数ψ(t)(高频分解)可表示为：

(13)

(14)

式中：h0k为高通正交滤波器系数；h1k为低通正交滤波器系数。

不同子频带和不同分解层数的小波包分解系数的迭代计算如下：

(15)

(16)

式中：Wi, j(k),k=1,2,…,N/2i为第i层第j个子节点处的小波包系数。

信号经过小波包分解以后，得到低频信号的近似系数和高频信号的细节系数，最底层各频段的近似系数和细节系数构成系数矩阵，然后将加速度传感器测得的3个方向(X、Y、Z)振动信号的小波包分解系数矩阵进行堆叠得到三维矩阵，具体过程如图8所示。

图8 小波包变换系数矩阵生成过程示意图

如图8所示，图中深色的模块为经过小波包变换以后的低频部分，原始信号经过多层小波包变换，得到了最后一层低频的小波包近似系数和高频的小波包细节系数，然后对得到的小波包系数进行重新排列，得到一个H×W×1的矩阵，3种状态Z方向的小波包系数图像化如图9所示。

然后，再对另外2个方向的原始信号进行相同的操作，将得到的3个方向的小波包系数矩阵进行堆叠，最终得到一个H×W×3的3通道小波包系数矩阵，3种状态的3通道小波包系数矩阵的图像化如图10所示。

图9 Z方向小波包系数图像化

图10 3通道小波包系数图像化

3.3 数据集说明

经过处理以后，最终得到只包含正常状态样本的训练集和包含正常与故障状态样本的测试集，具体描述如表1所示。

3.4 神经网络结构参数

卷积神经网络(convolutional neural networks，CNN)具有强大的特征学习能力[19]，并被广泛应用于故障诊断研究中的故障特征提取[20-21]，所以选择CNN提取目标样本的公共特征，经过多次连续测试，最终确定的神经网络结构如图11所示。deep SVDD的神经网络结构包含11层，其中卷积层的卷积核大小K×K均为5×5，步长s均为3，输出通道数C分别为32、64、128，使用的激活函数为LeakyReLU，参数α大小为0.2，Flatten层用于将上一层的输出变为一维，作为最后全连接层的输入，全连接层的节点数U为256。

选用的优化器为Adam，学习率为0.001，迭代次数(epoch)为50，批尺寸(batch size)为64。

图11 deep SVDD神经网络结构图

3.5 结果及分析

为了测试deep SVDD模型的性能，将与传统的用于故障检测的单分类模型OCSVM和SVDD进行对比。对于deep SVDD，每完成一次迭代训练，使用测试集评估模型。对于OCSVM和SVDD，使用径向基核函数，选择多组对模型性能影响较大的超参数gamma，范围为[0.001,0.3]，数据间隔为0.005 98，每改变一次超参数gamma，输出一次测试集的AUROC，通过设置多组不同的gamma寻找模型的最优解。各模型在测试集的AUROC结果曲线如图12所示，各模型在测试集的最大AUROC及对应的训练参数如表2所示。

图12 各模型在测试集的AUROC

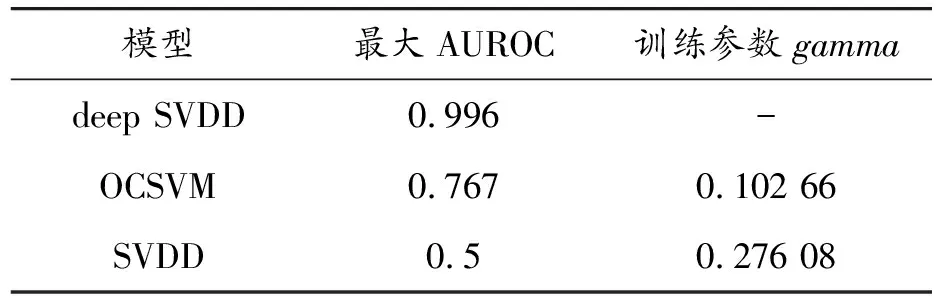
表2 最大AUROC及对应的训练参数

由图12可以看出，SVDD出现了AUROC小于0.5的情况，说明SVDD模型的性能甚至不如随机猜测，为了更客观地对比模型的性能，并未对AUROC小于0.5的情况进行反预测，即并未将标签进行翻转处理。

由表2可以看出，deep SVDD在测试集的最大AUROC为0.996，OCSVM的最大AUROC出现在gamma为0.102 66时，AUROC为0.765，所以deep SVDD可以准确地将PRSM正常状态和故障状态的数据进行区分，而OCSVM和SVDD的效果较差。由图12可以看出，deep SVDD收敛速度快，整个过程平稳，随着训练迭代步数的增加，在测试集的AUROC整体呈上升趋势且最后趋于稳定，而且远高于OCSVM，同时可以看出，OCSVM的性能受gamma值影响较大，测试集的AUROC随gamma值的变化发生较大波动，但整体AUROC较低，无法准确地将正常状态和故障状态的数据进行区分，而且通过对比deep SVDD和SVDD可以看出，采用神经网络提取特征效果更好。

由于SVDD出现AUROC小于0.5的情况，模型效果较差，故只展示deep SVDD和OCSVM(gamma=0.102 66)的ROC曲线，如图13、14所示。

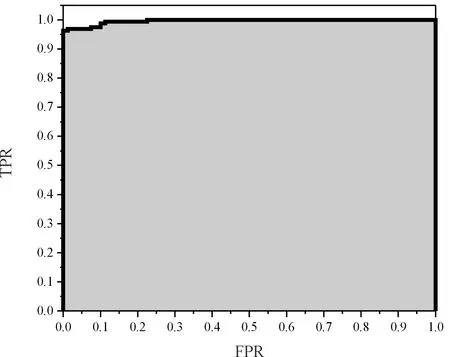
图13 deep SVDD模型的ROC曲线

图14 OCSVM(gamma=0.102 66)模型的ROC曲线

图13、14中，FPR指的是状态为故障(润滑失效和滚柱一侧断齿)的样本中，模型输出结果为正常状态的样本所占的比例，TPR指的是状态为正常状态的样本中，模型输出结果为正常状态的样本所占的比例，阴影部分为AUROC。可以明显看出，deep SVDD的AUROC大于 OCSVM(gamma=0.102 66)的AUROC，证明deep SVDD模型在测试集的表现最好。

将通过图15所示的测试集中正常状态和故障状态的原始数据分布图来分析各模型性能不同的原因。

图15 测试集原始数据分布

由图15可以看出，在低维空间中，正常状态和故障状态的数据混合在了一起，二者之间无明显的分类界面，所以难以应用于高维数据的 OCSVM和SVDD模型性能较差，而deep SVDD通过神经网络提取特征为低维到高维的过程，进而在高维空间中建立超球体，可以避免在数据混杂的低维空间中寻找分类界面，所以使用神经网络提取特征的deep SVDD模型性能较好。

为了对比模型的训练效率，表3列出了各模型训练所用的时间，其中deep SVDD为模型训练50次，以寻找最佳网络权重参数的总时间，OCSVM 和SVDD是模型对50个gamma值进行训练的时间，为模型训练50次以寻找最优gamma值的总时间，所以表3中列出的为3个模型各自训练50次所需要的总时间。由表3可以看出，deep SVDD训练时间最短，训练效率最高，OCSVM训练时间最长，远大于deep SVDD和SVDD训练所用的时间。

表3 各模型训练时间

综合以上，deep SVDD性能最佳，在测试集的AUROC可以达到0.996，而且训练速度快，50次迭代只需要17s，非常适合用于PRSM的故障检测。对于OCSVM和SVDD，gamma和核函数的选择需要一定的经验，在训练模型时，不可能对所有的取值进行训练，所以只能选择某些离散的取值，这给模型的训练和评估带来一定的困难。

4 结论

1) deep SVDD在测试集的AUROC高达0.996，训练效率高，50次迭代训练只需要17s，模型的整体性能优于OCSVM和SVDD，非常适合应用于PRSM的故障检测。

2) 采用CNN组成的神经网络提取样本特征，能够很好地实现目标样本公共特征的提取，并获得一个性能优异的deep SVDD模型。

3) deep SVDD超参数少，模型训练简单，OCSVM核函数和gamma的选择依赖一定的经验，而且无法对所有的gamma进行取值训练，在一定程度上增加了模型的训练难度。

4) SVDD出现了AUROC小于0.5的情况，在测试集的表现甚至不如随机猜测，所以不适合用于PRSM的故障检测。