纯电动汽车经济性巡航速度规划及控制方法设计
黄爱宝,盘朝奉,梁 军,王丽梅,徐 兴,何志刚
(1.江苏大学 汽车工程研究院, 江苏 镇江 212013;2.江苏大学 汽车与交通工程学院, 江苏 镇江 212013)
0 引言
自适应巡航控制(ACC)作为一种高级驾驶员辅助系统(ADAS),在推动汽车智能化发展的进程中扮演了重要的角色[1],其旨在自动化控制刹车和油门以实现定速巡航或者跟驰行驶,进而在一定程度上减轻驾驶员的负担[2]。在自适应巡航控制发展初期,更多注重车辆行驶安全性,这主要通过控制算法对主车的速度进行调节进而达到控制其和前车相对车速以及车间距的目的[3]。随着研究愈加成熟以及V2X技术的快速发展,更多的车辆行驶环境信息可以用于改善车辆的纵向控制以提高纯电动汽车行驶经济性[4]。电动汽车作为汽车未来发展的趋势,在众多的能源经济技术路线中,以生态友好、节能潜力巨大的特点得到了国内外众多学者的认可和推广[5],其摒弃了很多复杂的机械结构的同时增加了大量的电控系统,高度的集成控制使其在与ACC的融合设计方面有天然的优势。因此,众多学者对电动汽车的经济性巡航控制策略进行了深入的研究[6-9]。将纵向加速度作为模型预测控制的代价函数之一,试图通过减小车辆的加速度以期降低整车的能耗[10];基于纵向动力学模型将整车消耗功率建模为速度和加速度相关的函数,通过将车辆的功耗作为优化算法的目标函数以期优化整车的能耗[11]。由于经济性评价指标的建模精度与控制器所带来的经济性能改善密切相关,Jia等[12]提出基于电机转矩、转速和效率建立简化的线性电机能耗模型并将其作为模型预测控制算法的目标函数,通过对电机输出转矩优化从而改善了电机的工作点分布。初亮等[13]基于插值的方法建立非线性的电机能耗模型并使用非线性优化算法对多目标优化问题进行求解。上述建立经济性巡航控制器的方法多是通过选择合适的经济性评价指标作为目标函数之一以优化加速度或者电机转矩,从而在实现跟踪控制的同时降低整车的能耗,但是由电机能耗模型和车辆动力学模型等带来的非线性以及计算量大的问题是影响控制器实时应用的重要因素[14]。相关研究表明,在驾驶过程中为驾驶员提供有效的速度提示以减少频繁的速度波动,能够明显降低油耗[15]。因此,本文基于分层结构对经济性巡航控制器进行设计,通过缩小优化问题的规模,具体表现为将多目标优化问题分割成速度规划和跟踪控制2个模块,从而在一定程度上提高运算速度和改善优化效能。Andreas等[16]根据预先可知的未来出行信息使用动态规划(DP)算法离线获得了全局最优速度剖面,然后基于MPC来跟踪上述获得的速度曲线以实现在线控制,但是动态规划方法依赖于提前预知的未来出行信息且存在计算量较大的问题。郭露露[17]首先基于连续广义最小残差法对车辆通过交叉口的速度进行规划,其次基于最优控制原理获得了满足速度跟踪的最优转矩分配和最优挡位切换规律的显示解。基于解析的方法虽然有利于提高最优速度曲线的计算速度,但是适应性差,需要结合具体场景推导。Yang等[18]基于规则的方法提出匀加速-匀速车辆模型,求解车辆通过交叉口的最优车速,但是均匀变化的车速降低了规划车速的灵活性且无法协同优化规划车速对应的能耗。廖若桦[19]通过建立能耗模型作为智能优化算法的代价函数,确定交叉口下的通行约束条件对车辆连续通过交叉口的速度曲线进行求解以提高道路的通行效率并降低整车的能耗。上述研究的分层结构中的速度规划模块多是对车辆未来出行一段时间内的速度进行规划,但是车辆的实际行驶环境是不断变化的,因此需要根据车辆实时获得的环境信息对规划车速进行重新调整才能被跟踪控制器跟踪。综上所述,车速规划模块既要能提供未来一段时间内的最优速度曲线,如通过交叉口,又要能对短时域内的未来车速进行规划以应对复杂的行驶工况,如在城市道路中跟驰行驶时需要频繁地应对前车不断变化的行驶状态。Schmied等[20]基于二阶多项式非线性自回归模型引入前车的速度的预测,HIL实验表明燃油经济性得到显著提升。Zhang等[21]基于V2V和V2I获得的前面多车的速度、加速度和车间距等信息,使用贝叶斯网络(BN)对前车车速进行预测,同时考虑了分布式驱动汽车的前后驱动力矩的最优分配,结果表明:基于V2X通信信息的BN预测比传统的恒加速法具有更好的预测能力和节能效果。Dahmane等[22]基于马尔可夫决策过程对车辆的需求功率进行预测并将其作为模型预测控制框架的输入以对整车能耗进行优化。
针对现有研究存在的工况适应性差的不足,本文首先基于长短期记忆模型和遗传算法对处于不同行驶模式下的电动汽车速度进行规划,进一步提出了一种经济性巡航速度规划及控制方法,使车辆在不同行驶环境下都能够保持较优的经济性能。
1 建模
1.1 经济性巡航控制系统整体结构
图1所示为本研究所提出的经济性巡航控制系统整体结构,上层速度规划模块根据传感器获得的周围行驶环境判断车辆当前所处的驾驶模式并进行短期或长期速度规划。在跟驰行驶模式下,由于主车的行驶性能主要受前车行驶状态变化的影响,此时速度可优化空间不大,因此本文选择前车在预测时域内由LSTM模型预测得到的速度序列作为主车的规划车速,此预测车速序列转化为预测加速度序列可以作为扰动引入至模型预测控制的预测方程中以提高主车对前车行驶状态变化的反应速度;在自主巡航模式下,选择车辆连续通过多个交叉口作为研究场景,以电机转矩作为优化变量并将电机能耗作为目标函数,在信号灯约束、速度约束和转矩约束下基于GA对车辆全局速度进行优化,使车辆能够以较优的能耗表现和较少的停车次数连续通过多个交叉口。下层控制器主要包括速度跟踪控制器和距离跟踪控制器,若处于跟驰行驶模式,以速度规划模块输出的前车预测加速度作为扰动,以参考车间距、实际车间距和相对车速等信息作为输入,以期望转矩作为输出实现距离跟踪;若处于自主巡航模式,以速度规划模块输出的最优速度剖面作为输入,以期望加速度作为输出从而实现速度跟踪。处于自主巡航模式时,控制器输出的期望加速度首先经逆纵向动力学模型转化为期望转矩,其次再输入至执行机构用于对制动状态下的期望制动转矩进行电液制动力分配并对电机输出转矩进行外特性限制,实际输出的电机转矩和液压压强作用于整车动力学模型以驱动车辆的前进,最终实现系统的闭环控制。本文剩余部分将分别对速度规划模块、经济性巡航控制器、执行机构、逆纵向动力学模型和纵向动力学模型等进行建模,通过仿真验证所提出的经济性速度规划及控制方法在提升车辆行驶经济性方面的有效性。

图1 经济性巡航控制系统整体结构框图
1.2 执行机构建模
经济性巡航控制系统的执行机构主要包括电机模型和液压制动系统模型。其中电机模型主要包括动态模型和能耗模型,前者用于模拟电机的动态迟滞特性,后者用于构建经济性评价指标。式(1)所示为电机动态模型对应的传递函数。
(1)
通过试验可以获得电机效率随转矩和转速的变化关系,基于试验数据使用多项式拟合可以得到如式(2)和图2所示的简化电机能耗模型。
(2)
式中:Pm为电机功率;nm为电机转速;Tm为电机转矩;ηm为电机效率;aij为拟合系数,i=1~6,j=1~6。

图2 简化电机能耗模型示意图
通过对电机功率进行积分可以得到电机能耗:
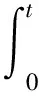
(3)
选择一阶等效电路模型对电池进行建模,根据基尔霍夫电压定律,上述各变量满足:
Ub=Eb-IbRb
(4)
式中:Eb为电池的电动势;Ub为电池的输出电压;Rb为电池的内阻;Ib为电池的电流。
研究表明,电池的电动势Eb和内阻Rb均与电池温度Tb和电池荷电状态SOC有关,通过实验可以拟合得到电动势和内阻与电池温度以及荷电状态之间的关系,如式(5)和式(6)所示[23]:
Eb=f1(SOC,Tb)
(5)
Rb=f2(SOC,Tb)
(6)
采用安时积分法对电池的SOC进行估算:
(7)
式中:SOCini为电池的初始SOC;CN为电池的额定容量;ηb为电池的效率。
1.3 逆纵向动力学建模
逆纵向动力学模型用于将期望加速度转化为期望转矩并使用转矩分配策略进一步将期望转矩划分为期望电机转矩或者期望液压压强。当期望加速度大于零时,基于式(8)将其转化为期望电机转矩Tdes;当期望加速度小于零时,首先基于式(9)将其转化为期望制动转矩Tx_des,然后基于式(10)计算得到当前车速下电机能够提供的最大电制动转矩Treg,如式(11)所示,不足的制动转矩由液压制动Pdes补偿。
(8)

(9)
(10)
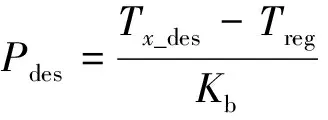
(11)
式中:m为整车质量;ades为期望加速度;δ为旋转质量换算系数;Cw为风阻系数;ρ为空气密度;A为迎风面积;g为重力加速度;f为滚动阻力系数;α为道路坡度;r轮胎半径;i为减速装置与主减速器的传动比乘积;ηt为传动系统的效率;r为车轮半径;vh为车速;fmot表示电机外特性。
1.4 车辆纵向动力学建模
车辆纵向动力学模型揭示了加速度与电机转矩之间的关系,如式(12)所示。滚动阻力、空气阻力和坡度阻力的计算如式(13)—(15)所示。
mdvh/dt=(Tmiηt)/r-Ff-Fair-Fi
(12)
Ff=mgfcosα
(13)
(14)
Fi=mgsinα
(15)
式中:Tm为电机输出转矩;Ff为滚动阻力;Fair为空气阻力;Fi为坡度阻力。
2 速度规划器
速度规划器根据车辆当前所处的行驶环境规划出最优的速度曲线以使车辆在完成既定的行驶任务时具有最优的性能表现。具体表现为:当车辆处于跟驰模式时,速度规划器为车辆提供短期规划车速以使主车能够及时响应前车行驶状态的变化,从而保证行驶的安全性和舒适性,本研究提出基于LSTM对前车在模型预测控制算法预测时域内的速度进行预测,并将其转化为加速度作为扰动引入到MPC控制器中以提高预测方程的精度;当车辆处于自主巡航模式时,速度规划器为车辆提供全局最优速度曲线以使主车以最小的能耗代价和停车次数连续通过交叉口,本研究提出基于GA对主车连续通过多个交叉口情景下的车速进行规划以提高道路的通行效率。
2.1 基于LSTM的短期车速规划
当主车处于跟随模式时,一般选择前车车速作为目标速度进行跟踪以保持安全的车间距。基于MPC框架的跟踪控制器需要前车在预测时域内的加速度作为扰动输入以完成状态向量的预测,因此选择将前车车速预测序列作为主车的短期规划车速。由于车辆速度一般不会发生剧烈的跳变,且会随时间呈现出一定的变化规律。长短期记忆模型是一种广泛用于时间序列预测的特殊的递归神经网络算法,相较于传统的RNN网络,LSTM可以学习长期的规律,从而解决了长期依赖的问题。LSTM通过增加门控如输入门、遗忘门和输出门,使自循环的权重保持不断变化,从而使历史信息有效地传递给相邻的LSTM单元。图3是LSTM单元的结构示意图。
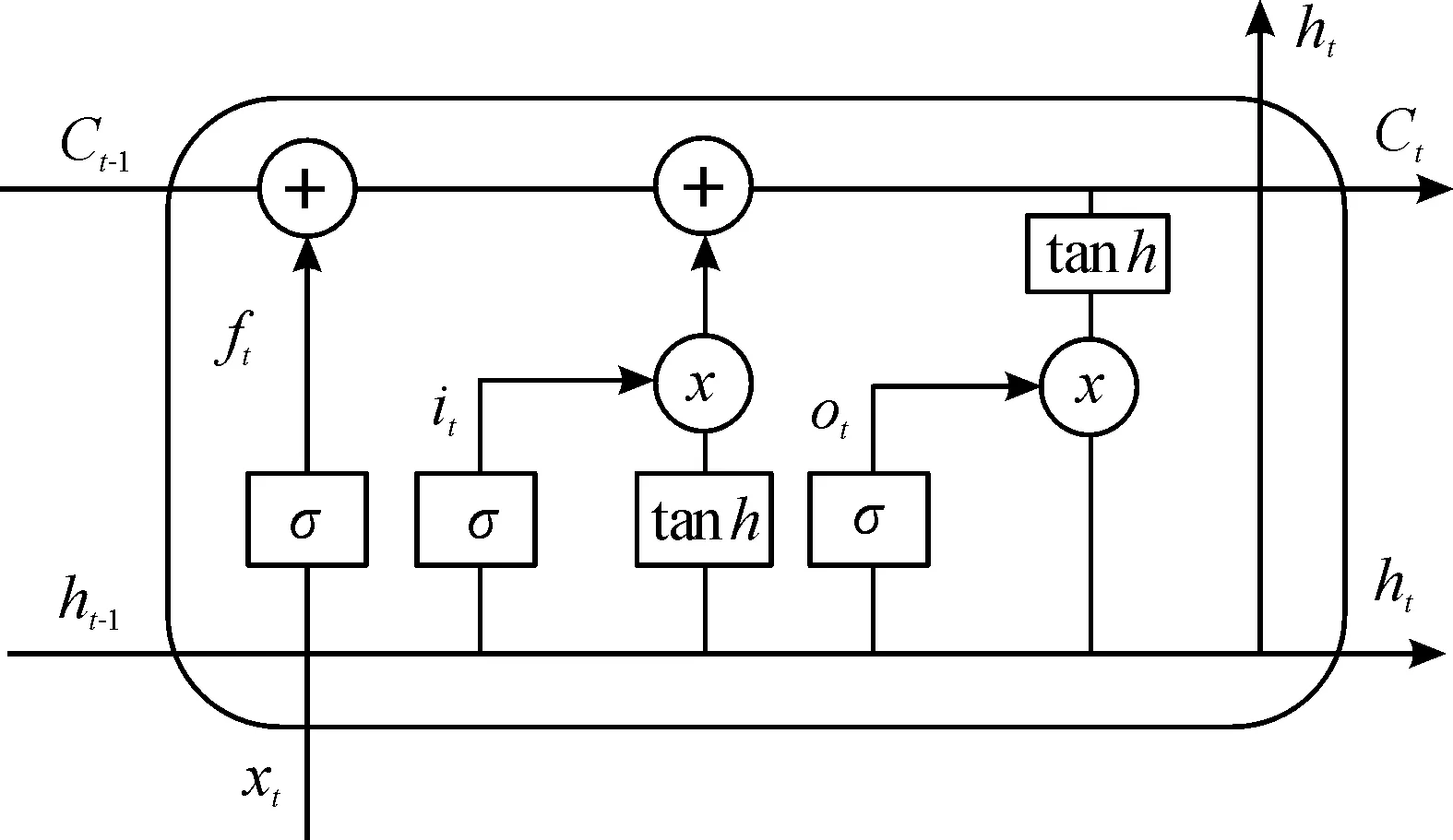
图3 LSTM的单元结构示意图
图3显示了LSTM单元可更新的输入参数Ct,它决定了信息是被遗忘还是传输到其他单元,更新Ct的过程如式(16)—(18)所示,模型的输出如式(19)—(20)所示。
ft=σ(wfx·xt+wfh·ht-1+bf)
(16)
it=σ(wix·xt+wit·ht-1+bi)
(17)
Ct=ftCt-1+it·tanh(wzxxt+wzhht-1+bz)
(18)
ot=σ(woxxt+wohht-1+bo)
(19)
ht=ot·tanh(Ct)
(20)
使用过去2 s内的前车历史速度序列作为LSTM模型的输入,以未来1 s内的前车预测车速作为输出。一次模型的训练输入是当前时刻下的速度,真值为下一时刻的真实车速,基于误差反向传播对模型参数进行更新。图4为CLTC-P工况下基于LSTM对未来5 s的速度进行多步预测获得的曲线。由图可知,无论是在加速阶段还是减速阶段,该模型能够很好地预测速度的变化趋势,车速预测值贴近真实的速度变化曲线,这表明LSTM具有较高的预测精度。
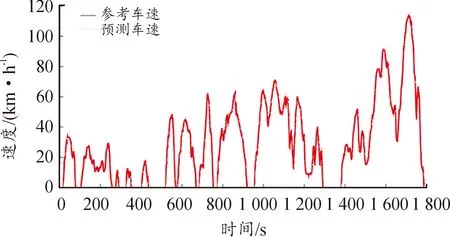
图4 CLTC-P工况下速度预测曲线
2.2 基于GA的长期车速规划
遗传算法是一种常用的数值优化算法,通过模拟生物界“适者生存,优胜劣汰”的生存机制实现优化算法的迭代。被编码成“染色体”的可能解易于模拟生物遗传时所发生的交叉和变异行为,基于个体的适应度选择部分父代用于产生新的子代以对待优化序列进行更新,随着迭部次数的增加,待优化序列可以逐步逼近最优序列。遗传算法在实际应用中需要确定好适应度函数和约束条件,因此本节将对车辆连续提供过多个交叉口情境下的速度规划模型的目标函数和约束条件进行构建。
当车辆处于自主巡航模式时,由于没有其他车辆的干扰,主车的目标行驶速度有较大的优化空间,比如在交叉口情景下,当基于V2X获得前方多个交叉口的信号灯状态信息时,速度规划模块可以对主车在未来一段时间内的速度轨迹进行优化,使其能够在不违反交通规则的情况下以最经济的车速连续驶过多个交叉口,从而提高出行效率。
记红灯时长为tred,绿灯时长为tgreen,黄灯时长为tyellow,因此信号灯的周期tcycle=tred+tgreen+tyellow。各交叉口之间的距离为xTLj,路口长度为xgap。tj为初始速度规划时刻第j个交叉口的信号灯配时。车速规划时长为tplanning,时间间隔Ts,因此待规划的车速序列长度N=tplanning/Ts,v0为初始规划时刻的速度。距离约束条件为Consj。

(21)
(22)
(23)
(24)
(25)

(26)
(27)
(28)
(29)
(30)
k1=iηt/(mr)
(31)
k2=-(gfcosα+gsinα)
(32)
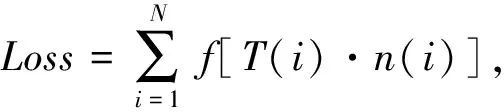
ifj=1
if TL=red
tgreen_start(i)=tj
Cons1=
N1=tgreen_start(1)/Ts
N2=(Tgreen_start(1)+tgreen+tyellow)/Ts
else
ift1+tyellow≥tmin
tgreen_start(1)=0
Cons1=
0.5Ts·E11[(K11T+K12+K21T+K22)Ts+2V0]≥xTL1+xgap
N1=[tgreen_start(1)+t1+tyellow]/Ts
else
tgreen_start(1)=t1+tyellow+tred
Cons1=
N1=tgreen_start(1)/Ts
N2=[tgreen_start(1)+tgreen+tyellow]/Ts
end
end
else
if TL=red
tgreen_start(j)=tj
Whiletgreen_start(j)≤tgreen_start(j-1)+tlim
tgreen_start(j)=tgreen_start(j)+tcycle
end
Consj=
N1=tgreen_start(1)/Ts
N2=[tgreen_start(1)+tgreen+tyellow]/Ts
else
tgreen_start(j)=tj+tyellow+tred
Whiletgreen_start(j)≤tgreen_start(j-1)+tlim
tgreen_start(j)=tgreen_start(j)+tcycle
end
Consj=
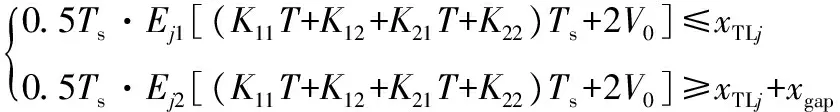
N1=tgreen_start(1)/Ts
N2=[tgreen_start(1)+tgreen+tyellow]/Ts
end
end
由表1可知,在第一个交叉口处,若信号灯为红色,则车辆需要等到绿灯开始后才能通过;否则将剩余信号灯时长与阈值tmin进行比较以决定是否等待下次绿灯开始再通过,同时记录下车辆选择通过第一个交叉口的时刻tgreen_start(1)。在第j个交叉口处,当绿灯开始的时刻与通过上一个交叉口的时刻tgreen_start(j)之差小于阈值tlim,即tgreen_start(j) 除了上述距离约束之外,还需要满足转矩及其增量约束、车辆加速度约束和路口限速约束。其中转矩及其增量约束表示为Tmin (33) 式中:amax表示路口加速度限值,速度约束表示为 (K11T+K12) 由第2节的分析可知,城市中行驶的车辆面临的场景大致可以分为自主巡航和跟驰行驶。当主车前方没有目标跟驰车辆时,基于速度跟踪控制器对规划车速进行跟踪,实现自主巡航;当前方存在目标车辆时,基于距离跟踪控制器实现跟驰行驶,从而与前车保持安全的车间距。因此,本研究主要对速度控制器和距离控制器进行设计。 基于复合趋近率的滑模控制器设计了速度跟踪控制器,自主巡航模式下的状态方程如式(34)所示: (34) 式中:ah为主车加速度;τ为时间常数;ades为待优化的目标加速度;vrel为车速误差,即期望车速和实际车速之差;x(k)=[vrel(k);ah(k)]。 选取滑模函数: s(k)=12(vrel_des(k)-vrel(k))+(ah_des(k) -ah(k))= Ce[R1(k)-x(k)] (35) 式中:R1(k)=[vrel_des(k);ah_des(k)],vrel_des(k)为期望车速误差,取为0;ah_des(k) 为期望的主车加速度,取为0。 基于式(34)和式(35),得到基于复合趋近律的速度跟踪控制律如式(36)所示: ades(k)=(CeB1)-1·[CeR1(k-1)- CeA1x(k)-s(k)-ds(k)] (36) (37) 基于模型预测控制设计距离跟踪控制器,将简化电机能耗作为经济性评价指标以期对整车能耗进行优化,两车跟驰行驶模型如式(38)所示: (38) 基于前向欧拉对上述公式进行离散化得到状态方程如式(39)所示: ζ(t+1)=Aζ(t)+BΔu(t)+Cap(t)+D (39) 式中: (40) (41) (42) (43) 由式(39)可知,基于当前时刻状态向量ξ(t)和前车加速度ap(t)便可递推得到下一时刻状态向量的预测值,其中ap(t)由车速规划模块输出的预测车速序列转换得到。如式(44)和式(45)所示,y1(t+1)为下一时刻的车间距和相对速度预测值,y2(t+1)为下一时刻的主车车速vh预测值。如式(49)和式(50)所示,Y1表示预测时域内状态量预测序列,Y2表示预测时域内的主车预测车速预测序列。因此,根据式(44)递推得到MPC预测时域内的状态量预测序列可以建立跟踪误差代价函数;根据式(45)递推得到主车车速预测序列和待优化的转矩序列可以建立电机能耗并作为经济性评价指标,其中预测电机转速和预测车速之间的转化关系如式(48)所示。 y1(t+1)=EAζ(t)+EBΔu(t)+ECap(t)+ED (44) y2(t+1)=FAζ(t)+FBΔu(t)+FCap(t)+FD (45) (46) (47) n=30vhi/(πr) (48) (49) (50) 因此,跟踪性评价指标、经济性评价指标和舒适性评价指标可以表示为: (51) (52) (53) 式中:R2(i)表示期望车间距和期望相对车速组成的向量,期望相对车速取为0,期望车间距由固定车头间距获得,如式(54)所示,其中th为固定车头时距,d0为最小停车间距。Np为模型预测控制的预测时域时长,Nc为模型预测控制的控制时域时长。 xrel_des=vhth+d0 (54) 使用权重参数将各评价指标组合在一起,得到模型预测控制的目标函数和约束条件如式(55)—式(64)所示: w3·Peconomy+w4·ε2 (55) ζ(t)=Aζ(t-1)+BΔu(t-1)+ Cap(t-1)+D (56) y1(t)=EAζ(t-1)+EBΔu(t-1)+ ECap(t-1)+ED (57) y2(t)=FAζ(t-1)+FBΔu(t-1)+ FCap(t-1)+FD (58) xrel(t)≥d0-ε1 (59) Δumin-ε2≤Δu(t)≤Δumax+ε2 (60) amin-ε3≤ah(t)≤amax+ε3 (61) jmin-ε4≤jh(t)≤jmax+ε4 (62) Tmin≤Tdes(t)≤Tmax (63) εmin≤ε≤εmax (64) 式中:w1、w2、w3和w4为各性能指标的权重参数;ε为放缩因子用于扩大可行解的范围。式(59)用于保证实际车间距始终大于安全阈值。式(60)—式(64)分别用于对转矩增量、主车加速度、主车加速度变化率和输出转矩进行幅值约束。 本部分在中国乘用车工况CLTC-P工况和交叉口情景下对上述车速规划算法和跟踪控制器的有效性进行验证。CLTC-P参考WLTC方法,去掉了与实际工况不符的超高速行驶部分,将行驶工况重新划分为3个速度区间,分别为低速、中速和高速。工况时长共计1 800 s,其中低速区间时间比例为37.4%,中速区间时间比例为38.5%,高速区间时间比例为24.1%。整个工况的平均车速为29.0 km/h,最大车速为114.0 km/h,怠速比例为22.1%。 将所提出的经济性巡航控制器(MPC+)与LQR控制器、SMC控制器和传统的MPC控制器进行对比,从车间距跟踪曲线、速度跟踪曲线、电机转矩曲线和电池SOC下降曲线分析所提出的控制器的优势。 仿真模型中的参数如表2所示。 表2 仿真参数 在CarSim软件中设置前车的目标车速为CLTC-P工况,可以进一步测试主车在该工况下使用经济性巡航控制器时的跟驰性能和经济性能。图5—8为4种不同控制器下的车间距跟踪曲线图。 图5 MPC+控制器距离跟踪曲线 图6 MPC控制器距离跟踪曲线 图7 LQR控制器距离跟踪曲线 图8 SMC控制器距离跟踪曲线 由图5—8可知,当不考虑经济性评价指标时,LQR控制器、SMC控制器和常规MPC控制器均可以实现较好的车间距跟踪,MPC+将电机能耗作为经济性评价指标并对权重参数进行动态调整,当期望车间距较小时,增大车间距权重参数并减小经济性权重参数可以保持较好的跟踪性能,从而保证行驶安全性;当期望车间距较大时,适当减小车间距权重参数并增大经济性权重参数虽然会使车间距跟踪性能略微降低,但减小转矩输出可以降低整车能耗,且较大的车间距使车辆在紧急制动的情况下有足够的制动距离,进而提高了紧急制动工况下的安全性。 图9为4种不同控制器下的速度跟踪曲线。由图可知,主车在不同控制器下均能够保证良好的速度跟踪。其中,由于MPC+引入了短期车速规划,在车辆启动加速的时候能够以更快速度跟踪前车的速度变化,而在制动时能够以更大的减速度跟踪前车的制动行为,一方面可以提高主车对前车行为的响应速度,另一方面可以使车辆以更大的电制动转矩制动,从而提高制动能量回收效率。 图9 不同控制器下的速度跟踪曲线 图10—12为不同控制器下的电机输出转矩曲线。由图可知,相较于MPC控制器,引入电机能耗至MPC+控制器可以有效减少电机转矩的波动,适当降低驱动转矩可以避免动力电池持续大功率输出,同时增大电制动转矩的峰值可以提高制动动能的回收,因此在一定程度上能够提高能量的利用率,降低整车能耗。相较于LQR和SMC控制器,在高速工况下,MPC+控制器对应的驱动转矩输出曲线大部分时刻处于下方,当车间距误差较大时会适当增加转矩输出以减少距离跟踪误差。此外,MPC+控制器还可以避免SMC控制器偶发的转矩振荡的情况,从而提高乘坐的舒适性。 图10 MPC+和MPC控制器下电机输出转矩曲线 图11 MPC+和LQR控制器下电机输出转矩曲线 图12 MPC+和SMC控制器下电机输出转矩曲线 图13为不同控制器下电池SOC下降曲线,由图可知,MPC+控制器、MPC控制器、LQR控制器和SMC控制器的终止SOC分别为0.827 5、0.825 8、0.824 0和0.825 0。这验证了引入电机能耗作为经济性评价指标可以有效降低电池的能量损失。 图13 不同控制器下的电池SOC下降曲线 进一步验证长期车速规划在提高整车经济性能方面的有效性,选择了车辆连续通过4个交叉口的情景作为研究背景,通过将GA优化得到的车速曲线和典型的手动驾驶得到的车速曲线进行对比分析来验证引入长期车速规划的优势。 图14为GA规划车速和典型手动驾驶车速的曲线,由图可知,典型的手动驾驶策略以匀速-匀加速-匀速-匀减速-匀速-匀加速-匀速的方法连续通过了4个交叉口,其中在第3个交叉口还停车等待了一段时间直至信号灯变为绿色才开始起步加速通过,而GA优化得到的速度曲线仅以一次加减速就可以连续通过4个交叉口,同时并没有出现减速至零停车等待信号灯变为绿色的情况,从而减少了车辆频繁的加减速和起步带来的能量损失。 图14 速度曲线 图15为4个交叉口信号灯约束下车辆行驶的位移曲线,由图可知,2种驾驶策略均能够在遵守交通规则的情况下连续驶过交叉口,但是GA对应的位移曲线变化更为平缓,即相应的速度变化平稳,这与上述速度对比图分析的结果一致,有利于提高乘客的驾驶体验。 图15 位移曲线 图16为2种驾驶策略对应的电机输出转矩曲线,由图可知,GA算法对应的车速的电机输出转矩幅值不大,维持在-10~10 N·m,但是转矩变化较为频繁,这是因为GA首先对各时刻下的速度进行离散化,随后再迭代优化,连续2个时刻下的速度难以保证曲率的连续,从而导致转矩变化频繁,对GA得到的速度曲线进行拟合或者滤波可以平滑规划车速;手动驾驶策略对应的电机转矩幅值变化较大,在-30~50 N·m,因此会造成更高的电机能耗,从而降低整车的经济性。 图16 扭矩曲线 针对传统的自适应巡航控制算法在降低整车能耗方面的不足,提出基于速度规划的经济性巡航控制设计方法。基于长短期记忆模型和遗传算法分别设计了短期车速规划和长期车速规划,将简化电机能耗作为优化问题的目标函数可以从降低能耗的角度对车速或者电机转矩优化。将对所提出的经济性巡航控制器与LQR控制器、SMC控制器和传统的MPC控制器进行对比,发现引入车速规划模块可以有效降低车辆的能耗并提高出行效率。3 自适应巡航控制器设计
3.1 速度跟踪控制器


3.2 距离跟踪控制器



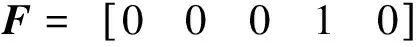
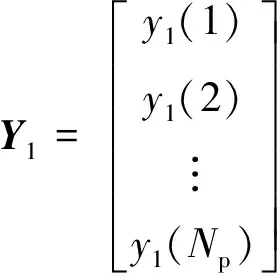
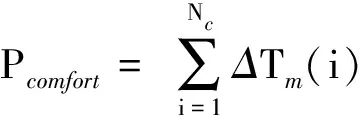
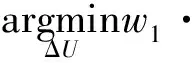
4 仿真结果验证
4.1 参数设计

4.2 CLTC-P工况下短期车速规划算法有效性验证






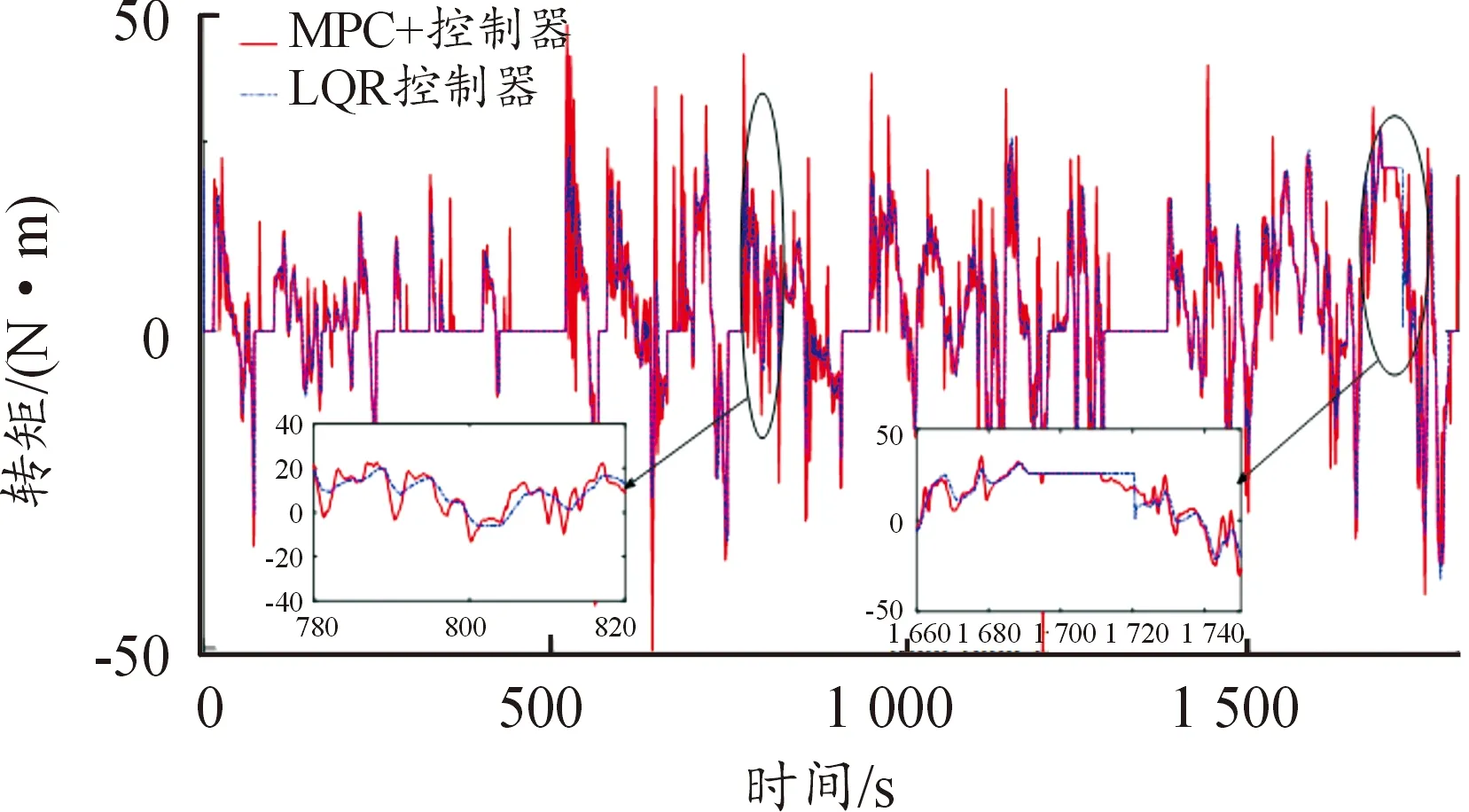

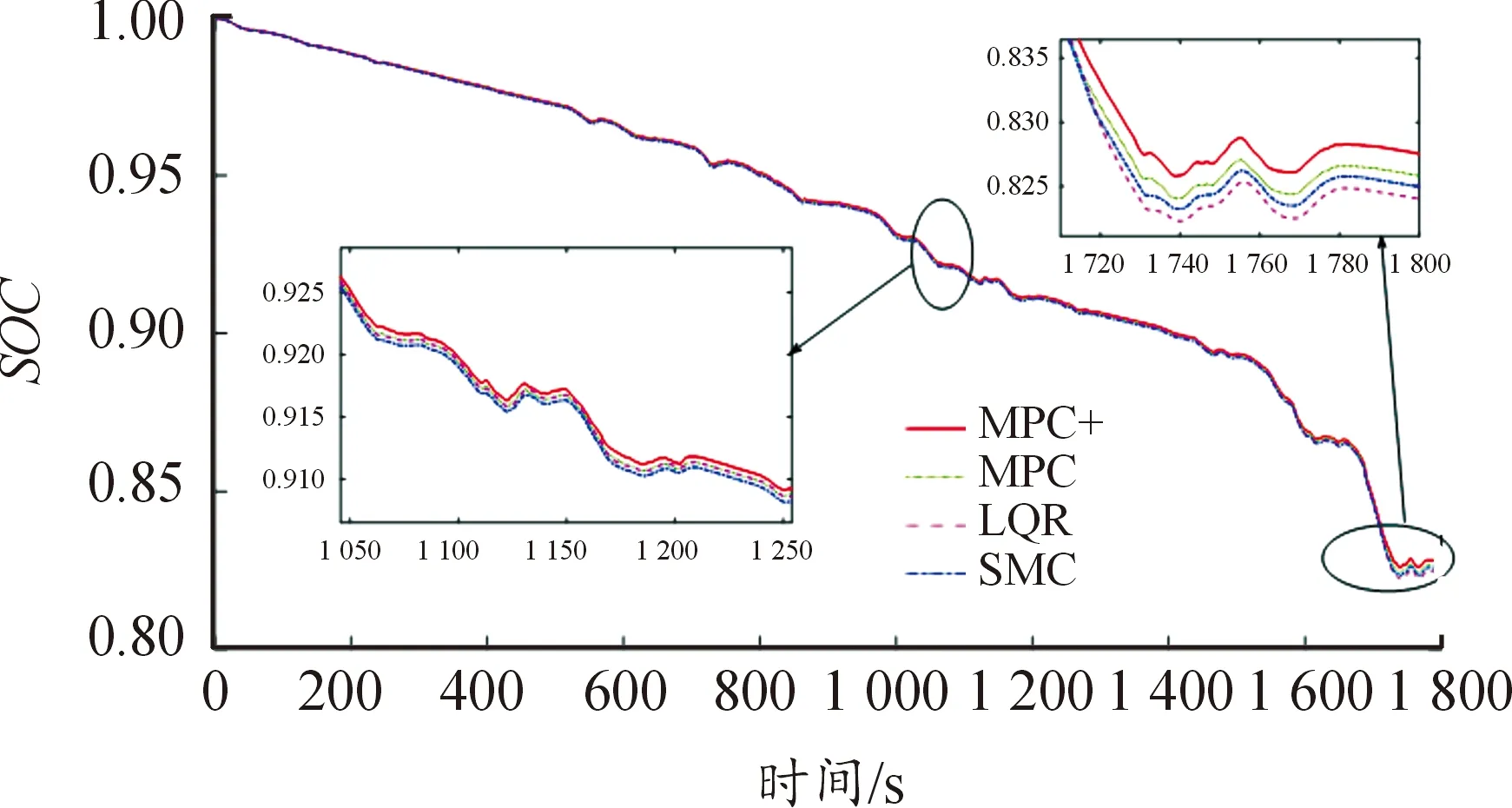
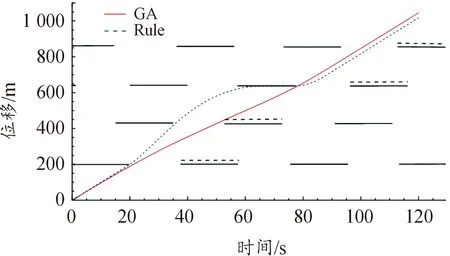
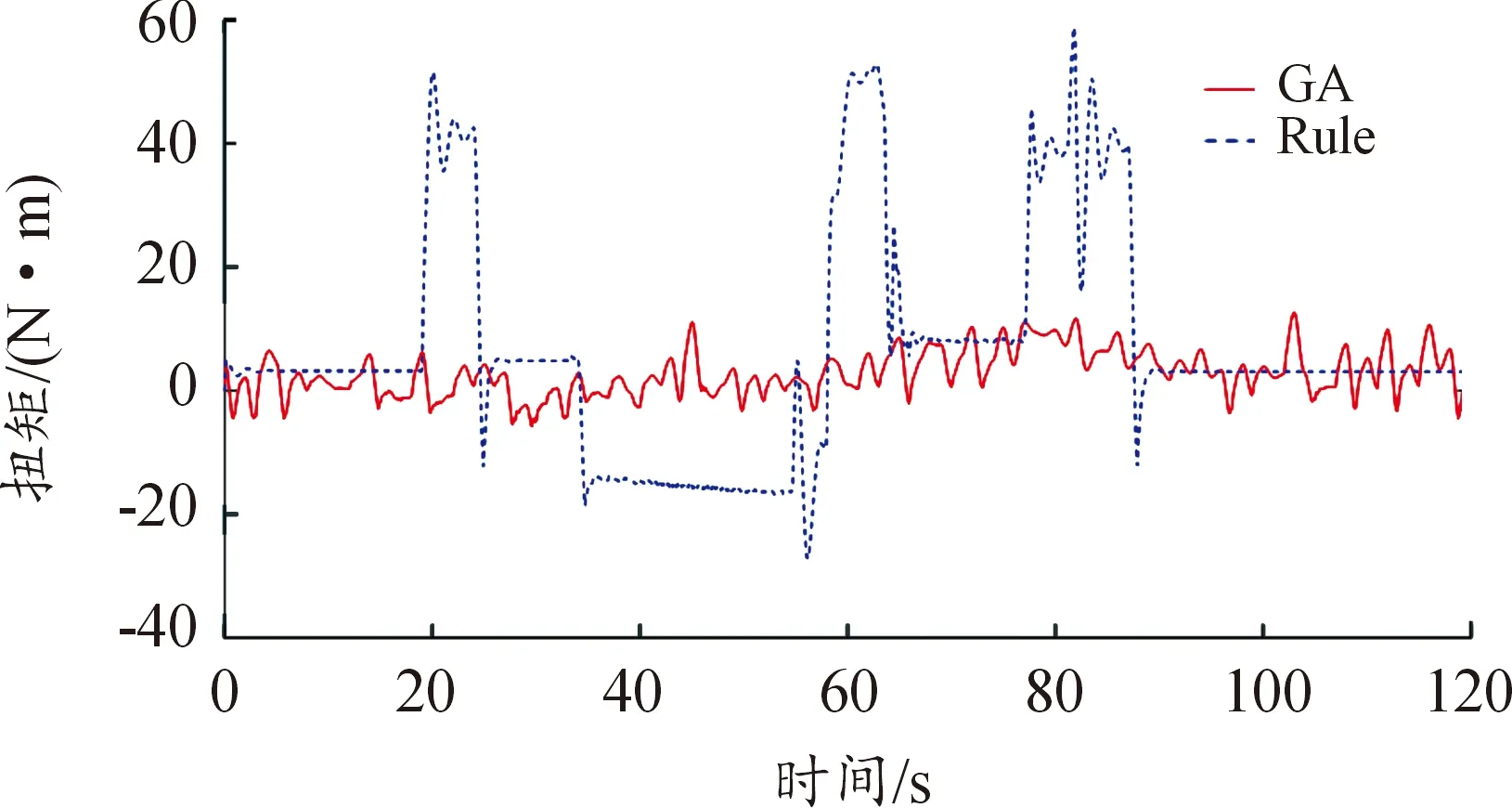
4.3 交叉口情景下长期车速规划算法有效性验证

5 结论

