充放电多特征融合的锂电池寿命预测方法

高静怡,陈首轩,周明博,曹军义

(西安交通大学 现代设计及转子轴承系统教育部重点实验室， 西安 710049)

0 引言

随着智能电网技术的发展和电动汽车产量的扩大，电池储能系统得到了快速发展[1-2]。锂离子电池以工作电压高、能量密度大、自放电效率低等优点在电动汽车领域得到了广泛应用[3]。为了保证电池的安全性和可靠性，健康状态(state of health，SOH)评估和剩余使用寿命(remaining useful life,RUL)预测成为工业界和学术领域研究的重要内容。

在进行电池的SOH评估及RUL预测时，直接指标参数主要有容量[4]和内阻[5]。Lai等[6]获得不同老化应力下4个电池循环老化的试验数据,研究了一种序贯扩展卡尔曼滤波器容量预测方法,并验证了方法的有效性。Li等[7]通过对U181850E电池实验数据分析，采用具有短期记忆的递归神经网络进行容量预测，生成了可行的估计结果。Remmlinger等[8]利用混合动力汽车运行期间的电池电压和电流数据对等效电路模型的内阻参数进行辨识，估计电池的退化情况,并利用单电池的测量数据进行验证研究。

上述研究表明，容量和内阻指标参数虽然都能够反映电池的老化状态，但通过上述方法进行二者的直接估计容易受环境因素影响，难以保证复杂工况条件下的准确可靠预测。因此，需要研究一种间接健康指标来表征锂离子电池的寿命状况，实现锂离子电池剩余寿命的在线预测。

Liu等[9]将等放电电压差的时间间隔作为特征指标，采用优化的相关向量机算法预测电池的剩余寿命，具有较好的预测精度和稳定性。Sun等[10]基于电容、电阻和恒流充电时间开发了一种综合健康指标，采用粒子滤波算法预测电池RUL，验证了方法的有效性。Wang等[11]以电池恒压充电阶段的电流变化率作为健康指标,利用Pearson和Spearman相关分析来评估健康指标与电池剩余容量之间的相似性,对电池RUL进行概率预测，验证了该方法的有效性。高栋等[12]将平均充电电流降作为特征指标,利用Box-Cox变换对其进行优化,提高了容量估计精度。Li等[13]对采用充电过程的容量增量曲线量化电池退化机制，分析得出电池容量与容量曲线上的位置之间存在线性回归关系,并开发健康估计函数，评估不同循环深度下的电池剩余寿命，具有较好的准确性。

综上，大多数间接指标只是从放电或者充电过程考虑。在充电过程中，汽车停止运行，测量数据比较平稳；而放电过程能够反映电池运行工况的复杂性。本文中通过分析电池充放电数据，综合考虑实际运行中电池变电流充放电的情况，提出一种充放电多特征融合指标表征电池的健康状况，进而设计卷积神经网络模型实现剩余寿命的在线预测。

1 电池健康状态特征提取

电池的老化是一个复杂的过程，受到多方面因素的影响。在电池的充放电循环中，电极和电解液之间不断发生反应，导致固体电解质界面生长和锂离子损失[14]。此外，循环会导致电极形态损伤和活性电极材料损失。一些极端操作条件(如过充、过放、高电压等)都会加速电池老化[15-16]。由于实际操作中容量和内阻难以测量，且运行工况复杂，通过充放电过程来研究电池的老化对实际运行的电动汽车健康评估至关重要。

本文中首先对NASA公开的B0005、B0006、B0007和B0018号电池循环老化数据进行分析，研究其老化过程中的电压动态变化规律和特征。

1.1 NASA锂离子电池数据分析

在电池老化实验中，充电模式为1.5 A恒流充电，当电压达到4.2 V后，保持恒压直至电流降至20 mA。放电模式为2 A恒流放电，直至电压下降至截止电压。为了观察电池不同的老化趋势，将截止电压分别设为2.7、2.5、2.2和2.5 V。

4个电池容量随着循环次数的变化曲线如图1。可以看出：随着循环次数的增加，电池容量呈衰减趋势，当衰减到失效阈值(国家标准中电动汽车动力电池容量降低为80%)以下可认为电池寿命结束。容量衰减曲线存在局部波动现象，这是由于实验过程中存在实验暂停。

另外，可以看出：B0005和B0007号电池在循环前期容量衰退曲线较为平缓，中后期衰退加快。B0006号电池衰退过程较为剧烈，这主要是由放电截止电压不同导致的。

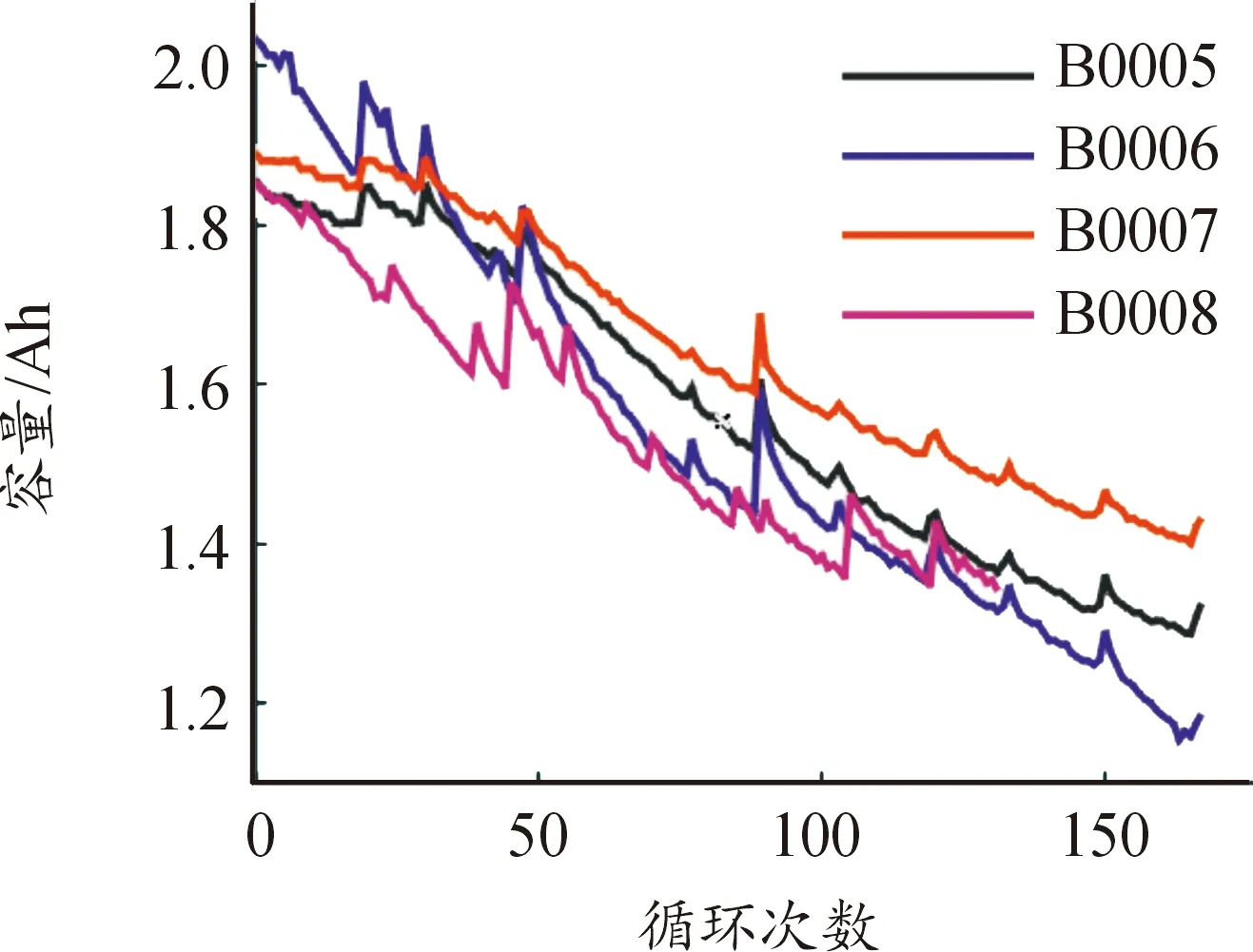
图1 NASA锂离子电池实际容量衰减曲线

1.2 放电过程特征提取

老化实验的B0005号电池在不同充放电周期内，其循环周期31、61、91和 121次中的放电电压曲线如图2。第31个周期放电结束时的时间为 3 326 s，而第61、91和 121周期时，时间分别为3 028、2 800和2 587 s，可以清晰看出电池的老化趋势。但这些数据是实验室理想情况下的测试数据，在实际工况下，每次都放电至截止电压是非常不现实的。若观测电池放电的中间阶段，即1 000～2 000 s，则发现不同放电周期的压降明显不同。如周期31时，1 000 s内的压降为 0.383 5 V,周期61、91和121次的压降分别是 0.384 2、0.384 9、0.385 6 V。

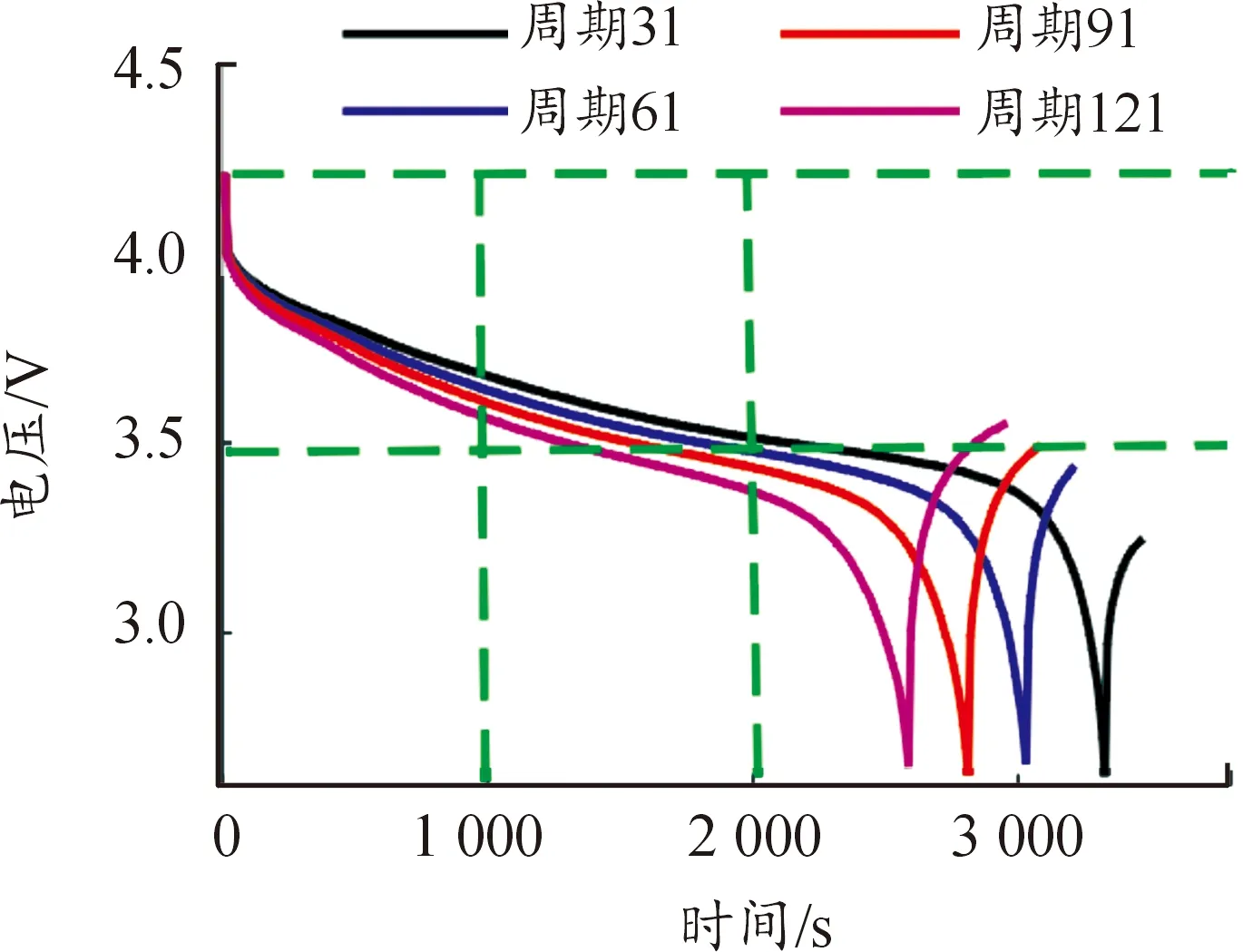
图2 B0005号电池放电电压曲线

根据图2中所示的放电电压曲线，可以获得等压降的时间和等时间内的压降。每个周期内，电压从一个较高值下降至一个较低值的时间呈减小趋势，而一定时间内的平均压降呈增大趋势。因此，可选择等压降放电时间和等时间平均压降来表征电池的寿命状况。

1) 等压降放电时间

选择4.2～3.5 V为等压降放电范围，则第i个放电周期对应的等压降放电时间为：

TFi=t4.2-t3.5

(1)

式中：t4.2为放电过程中电压为4.2 V时对应的时间；t3.5为电压下降至3.5 V对应的时间。则等压降放电时间序列可以表示为：

TF={TF1,TF2,…,TFk}

(2)

式中：k为放电周期数。

分别提取4个电池的等压降放电时间序列，并绘制其随放电周期变化的曲线，如图3。

从图3可以看出：以B0005号电池为例，其等压降放电时间从第1个放电周期的2 040 s，分别递减到第50、100和150个周期的2 006、1 509和1 266 s，其他3个电池与B0005号电池类似，等压降放电时间随着充放电循环的进行呈现明显的衰减趋势。由于截止电压预设值较大，B0005号电池在100个循环周期以后，等压降放电时间有一定的趋缓趋势，而B0006号电池的截止电压预设值较小，因此衰减速度更快。

2) 等时间内平均压降

由于老化实验过程中数据的采样间隔为17 s左右，因此选择59个在定义的时间范围内的采样点来计算。则第i个放电周期对应的等时间平均压降为：

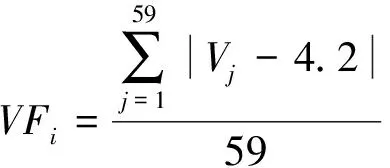
(3)

式中：Vj为每个采样点对应的电压;4.2表示电池的额定电压为4.2 V。则等时间平均压降序列可以表示为：

VF={VF1,VF2,…,VFk}

(4)

式中：k为放电周期数。

图4为4个电池的等时间平均压降序列随放电周期的变化曲线。由图4可知，B0005、B0006、B0007号3个电池在前30个循环的等时间平均压降存在异常，后期呈现增大趋势。通过与B0018号电池对比分析，可以判断B0005、B0006、B0007号3个电池在前期处于激活状态，因此取这3个电池30个循环后的等时间平均压降序列进行分析。

图4 等时间内平均压降曲线

1.3 充电过程特征提取

1) 恒压充电时间

B0005号电池在不同充放电周期内获得其循环周期31、61、91和 121次中的充电电压曲线，如图5。每个充电周期内，电压随着时间的变化呈现相同的变化趋势。在第31个充电周期中，恒压充电时间为6 416 s，而在第61、91和 121充电周期时，恒压充电时间分别为7 497、7 880和7 976 s，反映出电池的老化趋势。因此，可选择恒压充电时间来表征电池的寿命状况。

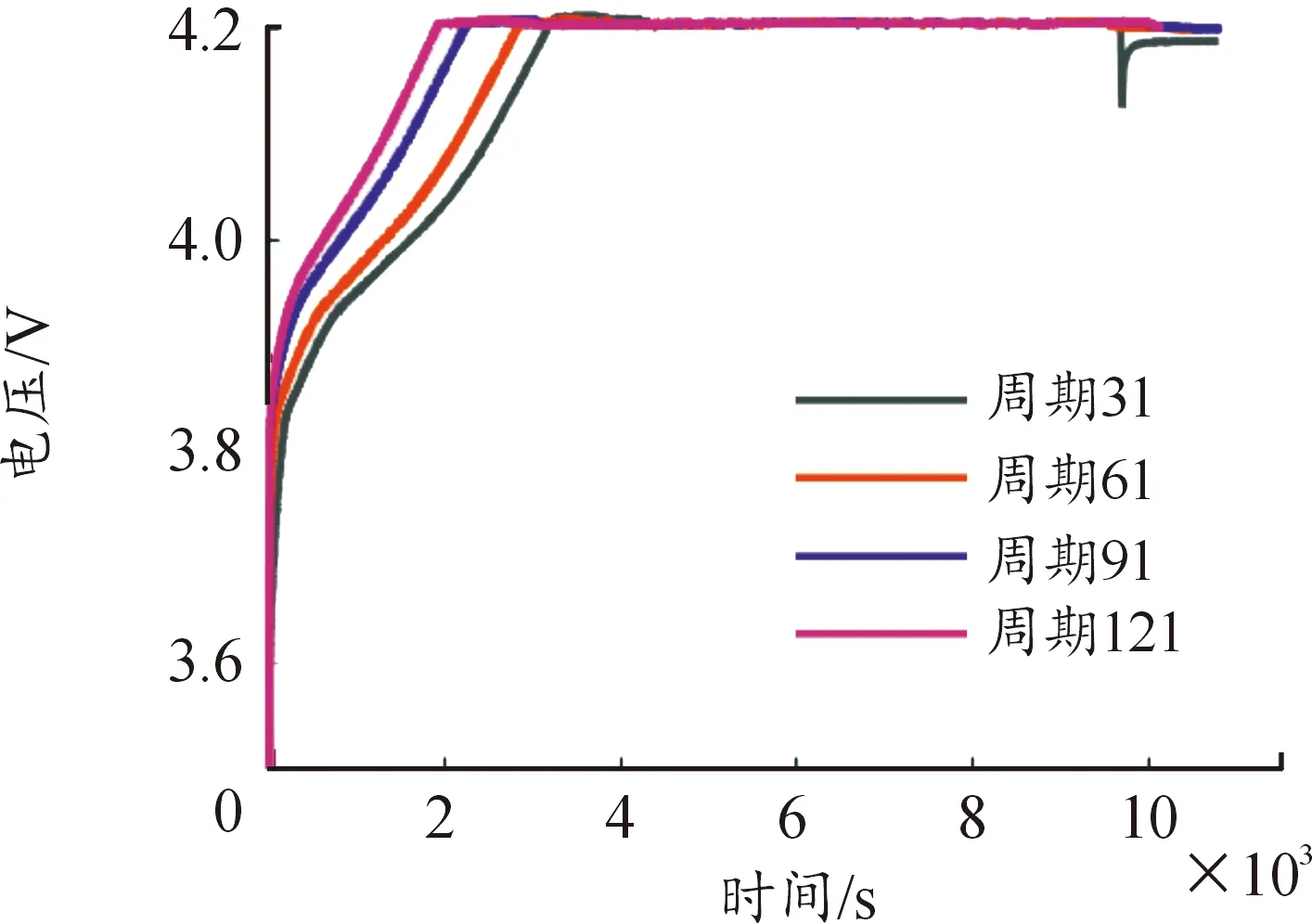
图5 B0005号电池充电电压曲线

根据图5中所示充电电压曲线，可以获得恒压充电时间。第i个充电周期对应的恒压时间为：

TCi=ti, j-ti,0

(5)

式中：ti, j为恒压充电过程终止点对应的时间；ti,0为恒压充电初始点对应的时间。各充电周期的恒压充电时间序列可以表示为：

TC={TC1,TC2,…,TCk}

(6)

式中：k为充电周期数。

分别提取4个电池的恒压充电时间序列，并绘制其随充电周期变化曲线，如图6。

图6 恒压充电时间曲线

与等时间平均压降类似，B0005、B0006、B0007号3个电池在前30个循环激活状态显著，在30循环后变化规律明显，后期呈现增大趋势。因此针对这3个电池，取30循环后的恒压充电时间序列分析。

2) 断电压降

电池在充电结束后存在压降现象。以B0005号电池为例，获得其循环周期31、61、91和 121次中的断电压降曲线，如图7。在第31个充电周期结束后，断电压降为0.191 7 V，而在第61、91和121充电周期，断电压降分别为0.195 0、0.199 4和0.207 3 V，随着循环的进行，断电压降逐渐增大。因此，断电压降可以用来表征电池的寿命状况。

图7 B0005号电池充电结束后电压曲线

根据图7中所示不同周期压降曲线，可以获得断电压降。第i个充电周期对应的断电压降为：

VCi=Vend-V0

(7)

式中：Vend为充电结束后的第1个采样点对应的电压；V0为电池的充电截止电压。则断电压降序列可以表示为：

VC={VC1,VC2,…,VCk}

(8)

式中：k为充电周期数。

分别提取4个电池单体的断电压降序列，并绘制其随充电周期变化曲线，如图8。

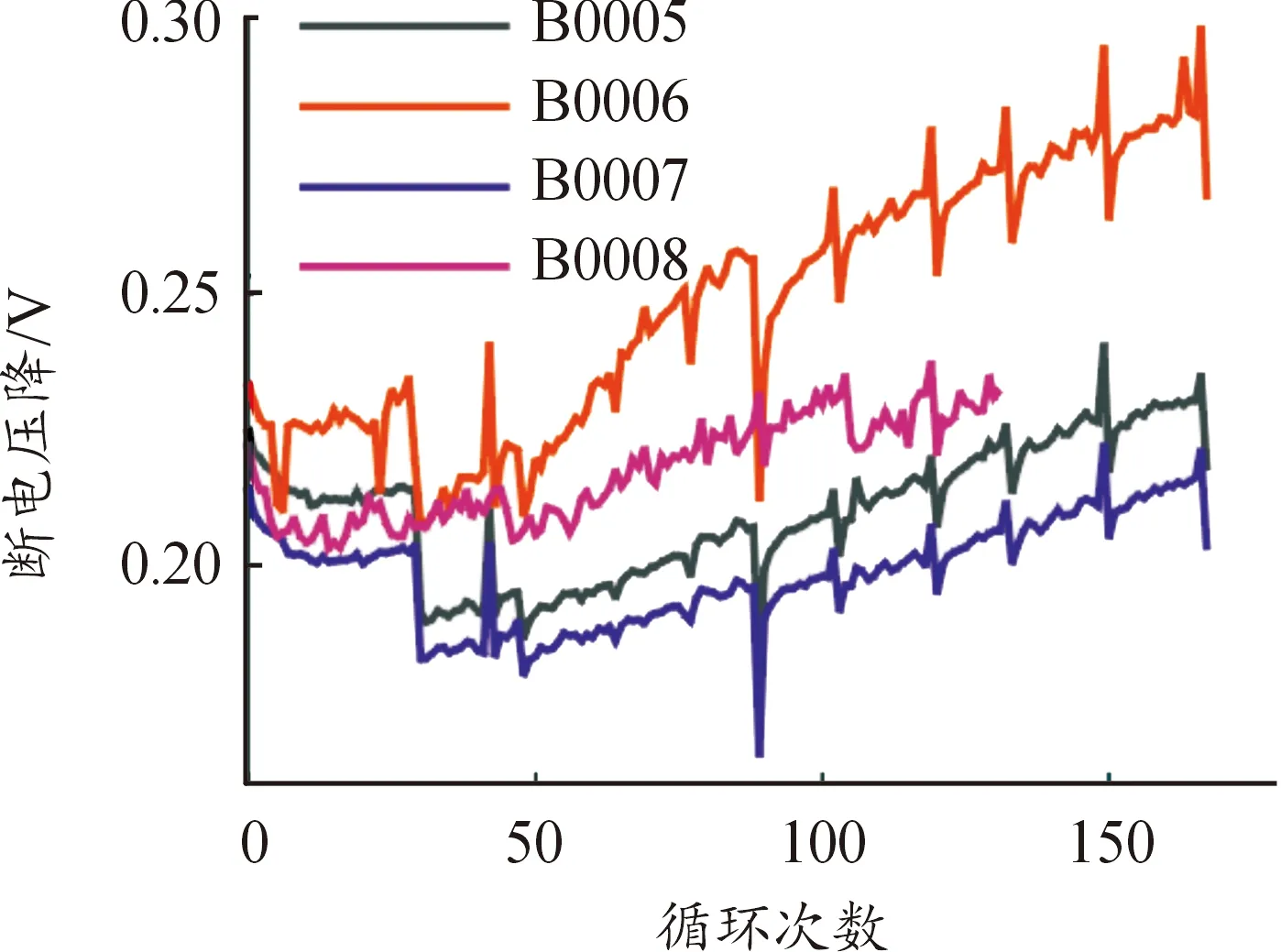
图8 断电压降曲线

该特征在前30个充放电循环中存在激活现象，但与等时间平均压降及恒压充电时间2个老化特征相比，激活状态不明显。断电压降曲线随着充放电循环的进行呈上升趋势，与容量衰减曲线类似。由于试验过程中存在暂停，故在个别充放电循环中存在突变现象。

1.4 相关性分析

针对上述老化特征，采用Pearson相关分析法来分析各特征与剩余容量之间的相关性。Pearson相关分析法可以定量反映两组数据间线性关系，其计算式如下：

(9)

若ρxy的计算结果为正，则变量X与变量Y正相关；计算结果为负，则变量X与变量Y负相关。ρxy绝对值越接近于1，表明变量之间的相关性越强；越接近于0，表明变量之间相关性越弱。当ρxy绝对值取值范围为[0.8,1]时，变量X与变量Y极强相关；取值范围为[0.6,0.8)时，变量X与变量Y强相关；取值范围为[0.4,0.6)时，变量X与变量Y中等程度相关；取值范围为[0.2,0.4)时，变量X与变量Y弱相关；取值范围为[0,0.2)时，变量X与变量Y极弱相关或无相关。

分别计算4个单体电池的各项老化特征与容量之间Pearson相关系数，结果如表1所示。

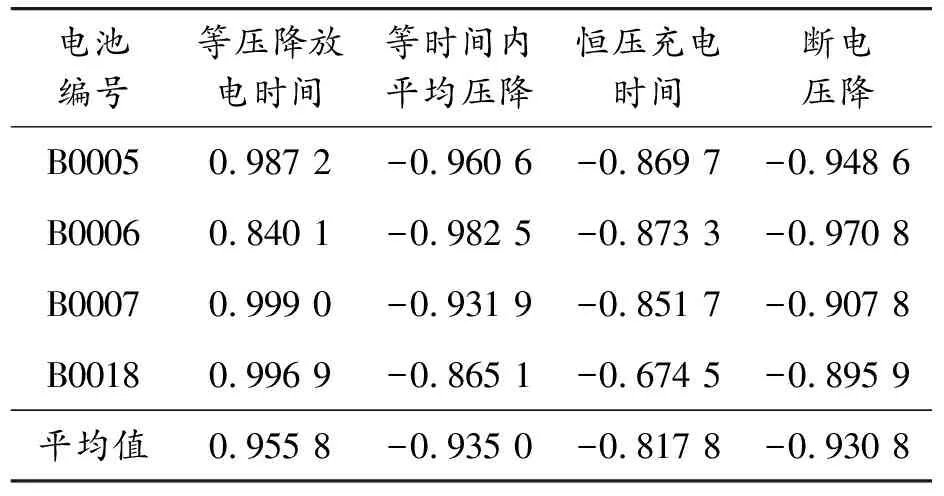
表1 各指标与容量之间的Pearson相关系数

由表1的计算结果可知，等压降放电时间、等时间内平均压降和断电压降3个老化特征与电池剩余寿命之间的相关性绝对值都在0.93以上，呈现出极强的相关性。而对于恒压充电时间，除B0018号电池外，其他3个电池的恒压充电时间与剩余容量之间相关性绝对值的平均值可以达到0.86以上，有强相关性。因此，所选4个老化特征可以用来构造剩余寿命指标。

2 融合指标构建方法

2.1 信息熵改进的灰度关联分析法

如果一个系统中既存在未知信息，也存在已知信息，那么就将这一类系统称之为灰色系统[17]。灰色系统理论主要是通过已知部分信息提取对评价结果有用的信息[18]。

灰度关联分析是灰度理论的一个分支，基本原理是根据各因素变化趋势的相似程度来判断不同因素间相关性。由于灰色关联分析法主要研究事物的变化，因此对样本数量的大小没有要求，也不需要样本数据具有典型的数学分布特征，计算量很小。因此本文中采用灰度关联分析计算融合指标序列。

由于各老化特征的量纲和单位不同，首先对每个特征进行标准化处理。对于随循环周期呈减小趋势的老化特征采用式(10)来标准化处理：

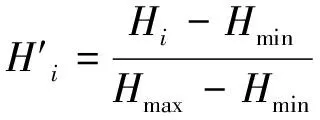
(10)

对于随循环周期呈增大趋势的老化特征采用式(11)来标准化量纲为一处理：

(11)

在式(10)和(11)中，H代表上文提取的老化特征，H′为标准化处理后的老化特征。

将以上的充放电老化特征进行标准化处理后，构建如下特征矩阵：

(12)

将特征矩阵中第1行数据作为参考序列，选定参考序列后，根据式(13)计算关联系数：

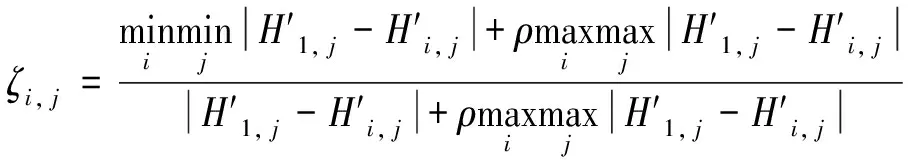
(13)

式中：ρ为分辨系数。

通过式(13)可以看出，当参考序列与比较序列差值为0时，关联系数取1。当差值最大时，关联系数取值为：

(14)

因此，关联系数取值范围为：

(15)

若关联系数的取值区间为[a，1]，则分辨系数的取值应当满足：

(16)

在计算灰色关联度时，忽视了系统中各项特征重要性程度的差异。为了衡量各个指标的权重，引入信息熵确定各指标的权重。该方法主要通过信息熵理论计算各特征的熵值，根据信息熵确定特征差异性，进而得到特征的权重[19]。特征的熵值越小，则在系统中所占的权重越大。基于信息熵改进灰度关联分析法的具体步骤如下：

步骤1计算第j项特征下第i个样本值的比重：

(17)

步骤2第j项老化特征的熵值为：

(18)

步骤3 根据指标熵值计算各项老化特征的权重：

(19)

步骤4最终得到的融合指标计算式为：

(20)

2.2 融合指标误差分析

通过上述分析，发现恒压充电时间和容量之间的相关性系数与其他3个指标相比较小，但可以通过信息熵分析降低这一指标的权重。

将标准化处理后的第1个循环周期老化特征作为参考序列，其余老化特征数据作为比较序列。

以电池单体的容量衰减作为标准判定融合指标的准确性。根据电池容量的衰减范围，分辨系数取值如表2所示。

表2 分辨系数取值

分别计算B0005、B0006、B0007、B0018号4个电池的融合指标并与容量定义的SOH值比较。4个电池融合指标与真实值的变化曲线如图9。

图9 锂离子电池健康状态融合指标计算结果曲线

分析图9中4个电池融合指标的均方根误差，B0005、B0007和B0018号3个电池的均方根误差分别为0.020 5、0.015 2和0.019 8，而B0006号电池在循环后期估算值与真实值之间的误差较大。但由于SOH值降至0.7之后，认为电池失效，所以后期的误差可以不列入考虑范围，因此B0006号电池融合指标的均方根误差为0.029 7。

为了证明所提出的充放电过程融合指标的准确性，分别将充电过程的2个特征指标和放电过程的2个特征指标进行融合，计算融合指标SOH与真实值之间的均方根误差，结果见表3。

由表3的均方根误差计算结果可知，4个电池的充放电融合特征指标预测误差均小于单一充电和放电特征指标的预测结果，平均可提升50%以上，且均方根误差平均为0.021 3，有较好的估算精度。因此，可以将充放电过程融合特征指标作为电池健康状态的表征，进而对电池的剩余寿命进行预测。

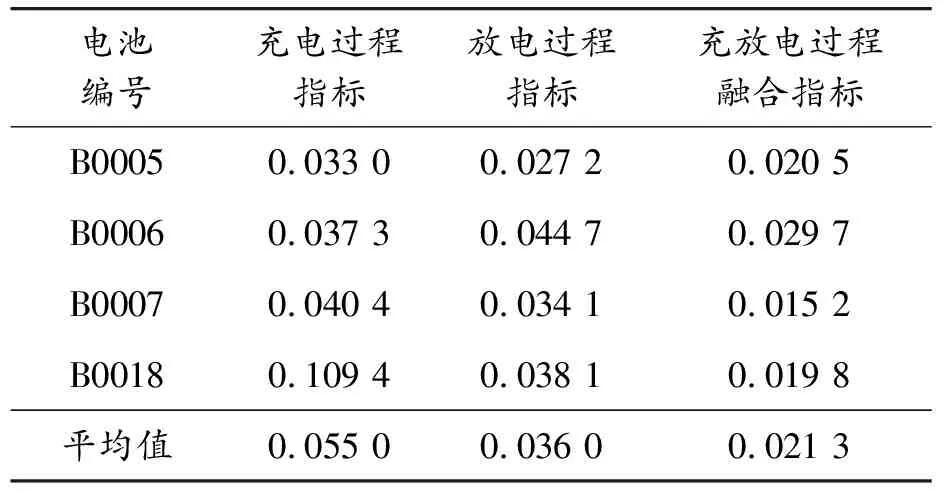
表3 误差计算结果

3 剩余寿命预测

3.1 卷积神经网络

电池是非线性系统，内部映射关系复杂。深度学习方法可以基于测量信号完成SOH估计，避免了对复杂非线性系统的建模过程，并且可以适应广泛的操作条件。在实际操作中，电池测量数据量大且种类多，而卷积神经网络的一大优势就是从大量数据中获取最有价值的信息，且泛化能力很强。因此，本文中选取卷积神经网络对电池进行寿命预测。

卷积神经网络通过多个非线性模块的组合构建输入数据到目标值之间的非线性映射，其结构主要包括5个卷积模块和3个全连接模块。每个卷积模块又由卷积层、批量归一化、激活函数组成。第1个卷积模块增加池化层用于激活函数的输出。批量归一化的作用是加速训练过程。激活函数将非线性因素引入网络模型中。5个卷积阶段之后是3个全连接层，最后1个全连接层由回归层接收。

卷积神经网络的优化算法采用自适应动量项算法。该算法利用梯度一阶矩和二阶矩估计自适应调整学习率，优点是经过偏置矫正后,可以修正一阶矩和二阶矩估计,使学习率有稳定范围[20]。

3.2 基于卷积神经网络的电池剩余寿命预测

电池的剩余寿命是指SOH衰减至失效阈值时所经历的充放电循环次数。将电池充放电循环内测得的电流、电压、温度数据离散化得到的矩阵做为输入，预测电池SOH衰减至失效阈值时的循环次数，输入结构为：

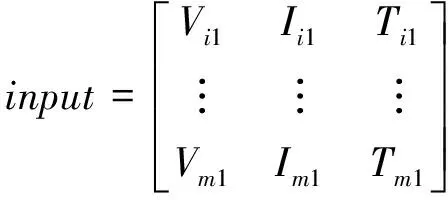
(21)

卷积神经网络的基本参数如表4所示。

表4 卷积神经网络参数

根据B0005、B0006、B0007和B0018号电池的容量衰减百分比，预设电池的失效阈值分别为0.75、0.70、0.80、0.75。

采用建立的寿命预测模型对电池进行寿命预测。随机初始化每层的权重，均值为0，标准差为0.01，偏差为0。将电池每个充放电循环的电压、电流和温度数据离散化成25×3的矩阵作为模型的输入。取前75个充放电循环的实测数据进行训练，将第76循环作为剩余寿命预测的起点，分别预测4个电池融合指标衰减至失效阈值时的循环次数。剩余寿命预测结果如图10所示。

图10 剩余寿命预测结果曲线

由图10(a)—(d)可以看出，以电池每个充放电循环内的实测数据作为输入，融合指标作为输出的剩余寿命预测结果非常接近前文所预设的失效阈值。

为了验证所建立的寿命预测模型的有效性，将提出的寿命预测结果与人工神经网络(artificial neural network,ANN)进行对比。ANN是六层前馈网络，包含75个输入神经元和1个输出神经元(即剩余寿命预测)。对比方法中：传统的ANN和建立的DCNN模型相应的网络参数保持不变。定义剩余寿命预测误差为：

(22)

其中：RULreal代表电池实际循环次数；RULpre代表预测达到的电池循环次数。表5给出了4块电池的预测误差。

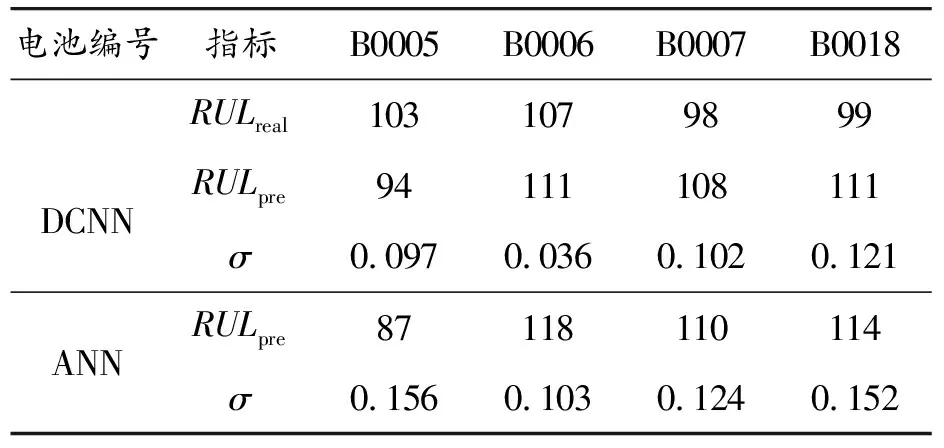
表5 剩余寿命预测误差

综合分析4个电池的预测结果，可以发现，在DCNN模型中4个电池的寿命预测值与真实值之间的差异在12个充放电循环以内，而在ANN模型中的预测偏差则在16个充放电循环以内，明显大于本文所提出的模型。进一步分析4个电池剩余寿命的相对误差，采用DCNN模型得到的寿命预测相对误差的平均值约为0.089；而采用ANN模型所得到的寿命预测相对误差平均值约为0.134，明显大于本文所提出的模型，证明了本文所提方法对电池寿命预测的精确性。

在验证模型预测精度的基础上，进一步对模型的预测稳定性进行分析。用SE(stability error,SE)代表电池剩余寿命预测的稳定性误差，定义稳定性误差为：

(23)

其中：RULpre代表预测的循环次数；SOHreal(i)代表电池某次循环的真实SOH值；SOHpre(i)代表电池某次循环的预测SOH值。表6给出了4块电池的稳定性误差。

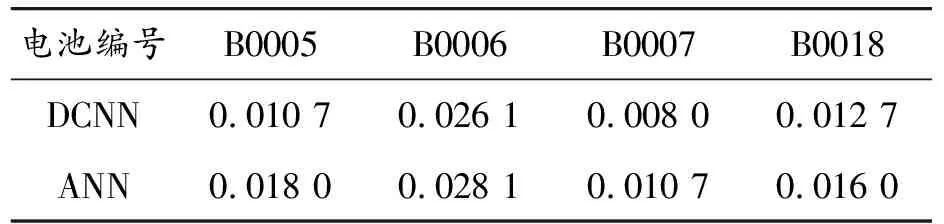
表6 剩余寿命预测稳定性误差

分析表6中所示的稳定性误差计算结果可知，DCNN模型中4个单体电池剩余寿命稳定性误差均在0.03以内，4个单体的预测稳定性误差平均值为0.016。ANN模型的预测误差稳定性误差也保持在0.03以内，但对比4个电池的计算结果可以发现，ANN模型的稳定性误差均大于DCNN模型，其稳定性误差计算平均值为0.018 0，大于DCNN模型，验证了DCNN模型的有效性。

4 结论

1) 等压降放电时间、等时间平均压降、恒压充电时间和断电压降4个特征指标可以表征电池的老化衰退，4个特征指标与电池剩余容量之间的相关性最大为0.955 8，最小为0.817 8。

2) 采用信息熵改进的灰度关联分析法对特征指标进行融合，得到的融合指标能够用来估算电池的健康状态，估算的均方根误差平均值为0.021 3。

3) 基于4个指标融合所得到的电池SOH估算序列，采用卷积神经网络对电池的剩余寿命进行预测，预测的平均误差为0.089 0，预测精度达到90%以上，并具有较好的稳定性。对于实车电池组剩余寿命预测有参考价值。